The main purpose of this paper is to study north–south Smale solenoid diffeomorphisms on $3$-manifolds by using affine Hirsch foliations. A north–south Smale solenoid diffeomorphism 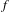$f$ on a closed $3$-manifold 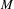$M$ is a diffeomorphism whose non-wandering set is composed of a Smale solenoid attractor 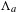$\unicode[STIX]{x1D6EC}_{a}$ and a Smale solenoid repeller 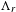$\unicode[STIX]{x1D6EC}_{r}$. The key observation is that a north–south Smale solenoid diffeomorphism 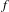$f$ automatically induces two non-isotopically leaf-conjugate affine Hirsch foliations 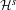${\mathcal{H}}^{s}$ and 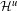${\mathcal{H}}^{u}$ on the orbit space of the wandering set of 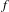$f$ (abbreviated to the wandering orbit space of 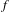$f$) by the stable and unstable manifolds of 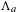$\unicode[STIX]{x1D6EC}_{a}$ and 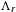$\unicode[STIX]{x1D6EC}_{r}$, respectively. Under this viewpoint, we build some close relationships between north–south Smale solenoid diffeomorphisms and Hirsch manifolds (the closed $3$-manifolds admitting two non-isotopically leaf-conjugate affine Hirsch foliations).

• ∙ On the one hand, the union of the wandering orbit spaces is nearly in one-to-one correspondence with the union of Hirsch manifolds.

• ∙ On the other hand, surprisingly, the topology of the wandering orbit space (Hirsch manifold) is nearly a complete invariant of north–south Smale solenoid diffeomorphisms up to semi-global conjugacy.

Moreover, as applications, we consider several more concrete questions. For instance, we prove that every diffeomorphism in many semi-global conjugacy classes of north–south Smale solenoid diffeomorphisms are not structurally stable.