Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-07-07T17:36:54.998Z Has data issue: false hasContentIssue false
  • English
  • Français

Strange attractor in the unfolding of an inclination-flip homoclinic orbit

Published online by Cambridge University Press:  14 October 2010

Vincent Naudot
Vincent Naudot
Affiliation:
Université de Bourgogne, Département de mathématiques, Laboratoire de topologie, U.R.A 755 21004 Dijon Cedex, France
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the unfolding of a smooth vector-field X on ℝ3 having a homoclinic orbit to a hyperbolic equilibrium point with three real eigenvalues satisfying − λss < λs < 0 < λu We say that Γ is an inclination-flip homoclinic orbit if the extended unstable manifold at the equilibrium point is, along Γ, non-transverse to the stable manifold and that Γ is of weak type if the unstable manifold has a non-trivial intersection with a special C2 weak stable manifold of dimension one. In this paper, we show the existence of a strange attractor in the unfolding of an inclination-flip homoclinic orbit (of weak type) in the case where the divergence at the equilibrium point is negative. 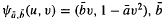The crucial idea is to compare the Poincaré return map with the Hénon family: being close to 0.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 16 , Issue 5 , October 1996 , pp. 1071 - 1086
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Bonckaert, P.. On the continuous dependence of the smooth change of coordinates in parametrized normal form theorems. J. Diff. Eq 106 (1993), 107–120.CrossRefGoogle Scholar
[BC]Benedicks, M. and Carleson, L.. The dynamics of the Hénon map. Ann. math. 133 (1991), 73–169.CrossRefGoogle Scholar
[D]Deng, B.. Homoclinic twisting bifurcation and cusp horseshoe maps. J. Dyn. Diff. Eq. 5 (1993), 417–467.CrossRefGoogle Scholar
[H]Hénon, M.. A two dimensional mapping with a strange attractor. Comm. Math. Phys. 50 (1976), 69–77.CrossRefGoogle Scholar
[Ho]J, A.. Homburg. Some global aspects of homoclinic bifurcations of vector fields. PhD Thesis, University of Groningen, 1993.Google Scholar
[HKK]J, A.. Homburg, H. Kokubu and M. Krupa. The cusp horseshoe and its bifurcations in the unfolding of an inclination-flip homoclinic orbit. Ergod. Th. & Dynam. Sys. 14 (1994), 667–693.Google Scholar
[HPS]Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics 583). Springer, Berlin, 1977.CrossRefGoogle Scholar
[MV]Mora, L. and Viana, M.. Abundance of strange attractors. Ada Math. 171 (1993), 1–71.Google Scholar
[N]Naudot, V.. Hyperbolic dynamics in the unfolding of a degenerate homoclinic orbit. Prépublication du Laboratoire de Topologie No 36. Université de Dijon, 1994.Google Scholar
[Ne]Newhouse, S.. Diffeomorphisms with infinitely many sinks. Topology 13 (1974), 9–18.CrossRefGoogle Scholar
[Py]Plykin, R.. On the geometry of hyperbolic attractors of smooth cascades. Russian Math. Surveys 39 (1984), 85–131.CrossRefGoogle Scholar
[PT]Palis, J. and Takens, F.. Hyperbolicity and Sensitive Chaotic Dynamics at Homoclinic Bifurcations, Fractal Dimensions and Infinitely Many Attractors. Cambridge University Press, 1993.Google Scholar
[R]Robinson, C.. Bifurcation to infinitely many sinks. Comm. Math. Phys. 99 (1974), 154–175.Google Scholar
[Ry]R, M.. Rychlik. Lorenz-attractors through Shil'nikov-type bifurcation. Part 1. Ergod. Th. & Dynam. Sys. 10 (1990), 793–821.Google Scholar
[S]Sandstede, B.. Verzweigungstheorie homokliner Verdopplungen. PhD Thesis, University of Stuttgart, 1993.Google Scholar
[Shi]P, L.. Shil'nikov. A case of the existence of a denumerable set of periodic motions. Sov. Math. Dockl. 8 (1965), 163–166.Google Scholar