Hostname: page-component-7479d7b7d-k7p5g Total loading time: 0 Render date: 2024-07-10T22:38:12.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly ergodic equivalence relations: spectral gap and type III invariants

Published online by Cambridge University Press:  27 November 2017

CYRIL HOUDAYER ,
AMINE MARRAKCHI  and
PETER VERRAEDT
CYRIL HOUDAYER
Affiliation:
Laboratoire de Mathématiques d’Orsay, Université Paris-Sud, CNRS, Université Paris-Saclay, 91405 Orsay, France email cyril.houdayer@math.u-psud.fr, amine.marrakchi@math.u-psud.fr, peter.verraedt@math.u-psud.fr
AMINE MARRAKCHI
Affiliation:
Laboratoire de Mathématiques d’Orsay, Université Paris-Sud, CNRS, Université Paris-Saclay, 91405 Orsay, France email cyril.houdayer@math.u-psud.fr, amine.marrakchi@math.u-psud.fr, peter.verraedt@math.u-psud.fr
PETER VERRAEDT
Affiliation:
Laboratoire de Mathématiques d’Orsay, Université Paris-Sud, CNRS, Université Paris-Saclay, 91405 Orsay, France email cyril.houdayer@math.u-psud.fr, amine.marrakchi@math.u-psud.fr, peter.verraedt@math.u-psud.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain a spectral gap characterization of strongly ergodic equivalence relations on standard measure spaces. We use our spectral gap criterion to prove that a large class of skew-product equivalence relations arising from measurable $1$-cocycles with values in locally compact abelian groups are strongly ergodic. By analogy with the work of Connes on full factors, we introduce the Sd and $\unicode[STIX]{x1D70F}$ invariants for type 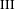$\text{III}$ strongly ergodic equivalence relations. As a corollary to our main results, we show that for any type 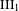$\text{III}_{1}$ ergodic equivalence relation 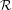${\mathcal{R}}$, the Maharam extension 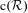$\text{c}({\mathcal{R}})$ is strongly ergodic if and only if 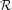${\mathcal{R}}$ is strongly ergodic and the invariant 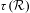$\unicode[STIX]{x1D70F}({\mathcal{R}})$ is the usual topology on 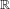$\mathbb{R}$. We also obtain a structure theorem for almost periodic strongly ergodic equivalence relations analogous to Connes’ structure theorem for almost periodic full factors. Finally, we prove that for arbitrary strongly ergodic free actions of bi-exact groups (e.g. hyperbolic groups), the Sd and $\unicode[STIX]{x1D70F}$ invariants of the orbit equivalence relation and of the associated group measure space von Neumann factor coincide.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 7 , July 2019 , pp. 1904 - 1935
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Austin, T. and Moore, C. C.. Continuity properties of measurable group cohomology. Math. Ann. 356 (2013), 885–937.Google Scholar
Akemann, C. A. and Ostrand, P. A.. On a tensor product C∗ -algebra associated with the free group on two generators. J. Math. Soc. Japan 27 (1975), 589–599.Google Scholar
Boutonnet, R., Houdayer, C. and Raum, S.. Amalgamated free product type III factors with at most one Cartan subalgebra. Compos. Math. 150 (2014), 143–174.Google Scholar
Boutonnet, R., Ioana, A. and Salehi Golsefidy, A.. Local spectral gap in simple Lie groups and applications. Invent. Math. 208 (2017), 715–802.Google Scholar
Brown, N. P. and Ozawa, N.. C∗ -Algebras and Finite-Dimensional Approximations (Graduate Studies in Mathematics, 88) . American Mathematical Society, Providence, RI, 2008.Google Scholar
Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.Google Scholar
Connes, A. and Jones, V. F. R.. A II1 factor with two non-conjugate Cartan subalgebras. Bull. Amer. Math. Soc. (N.S.) 6 (1982), 211–212.Google Scholar
Connes, A.. Une classification des facteurs de type III. Ann. Sci. Éc. Norm. Supér. (4) 6 (1973), 133–252.Google Scholar
Connes, A.. Almost periodic states and factors of type III1 . J. Funct. Anal. 16 (1974), 415–445.Google Scholar
Connes, A.. Outer conjugacy classes of automorphisms of factors. Ann. Sci. Éc. Norm. Supér. (4) 8 (1975), 383–419.Google Scholar
Connes, A.. Classification of injective factors. Cases II1 , II ∞ , III𝜆 , 𝜆≠1. Ann. of Math. (2) 74 (1976), 73–115.Google Scholar
Feldman, J. and Moore, C. C.. Ergodic equivalence relations, cohomology, and von Neumann algebras. I, II. Trans. Amer. Math. Soc. 234 (1977), 289–324; 325–359.Google Scholar
Haagerup, U.. Connes’ bicentralizer problem and uniqueness of the injective factor of type III1 . Acta Math. 69 (1986), 95–148.Google Scholar
Houdayer, C. and Isono, Y.. Bi-exact groups, strongly ergodic actions and group measure space type III factors with no central sequence. Comm. Math. Phys. 348 (2016), 991–1015.Google Scholar
Houdayer, C., Marrakchi, A. and Verraedt, P.. Fullness and Connes’ $\unicode[STIX]{x1D70F}$ invariant of type $\text{III}$ tensor product factors. Preprint, 2016, arXiv:1611.07914.Google Scholar
Jones, V. F. R.. Central sequences in crossed products of full factors. Duke Math. J. 49 (1982), 29–33.Google Scholar
Krieger, W.. On non-singular transformations of a measure space. I, II. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 11 (1969), 83–97; 98–119.Google Scholar
Krieger, W.. On ergodic flows and the isomorphism of factors. Math. Ann. 223 (1976), 19–70.Google Scholar
Kechris, A. S. and Tsankov, T.. Amenable actions and almost invariant sets. Proc. Amer. Math. Soc. 136 (2008), 687–697.Google Scholar
Marrakchi, A.. Spectral gap characterization of full type III factors. J. Reine Angew. Math. to appear. Published online 12 January 2017, doi:10.1515/crelle-2016-0071.Google Scholar
Moore, C. C.. Group extensions and cohomology for locally compact groups. III. Trans. Amer. Math. Soc. 221 (1976), 1–33.Google Scholar
Ozawa, N.. Solid von Neumann algebras. Acta Math. 192 (2004), 111–117.Google Scholar
Ozawa, N.. A Kurosh type theorem for type II1 factors. Int. Math. Res. Not. IMRN (2006), Art. ID 97560.Google Scholar
Ozawa, N.. An example of a solid von Neumann algebra. Hokkaido Math. J. 38 (2009), 557–561.Google Scholar
Ozawa, N.. A remark on fullness of some group measure space von Neumann algebras. Compos. Math. 152 (2016), 2493–2502.Google Scholar
Popa, S.. Some computations of 1-cohomology groups and construction of non orbit equivalent actions. J. Inst. Math. Jussieu 5 (2006), 309–332.Google Scholar
Schmidt, K.. Asymptotically invariant sequences and an action of SL(2, ℤ) on the 2-sphere. Israel J. Math. 37 (1980), 193–208.Google Scholar
Schmidt, K.. Amenability, Kazhdan’s property T, strong ergodicity and invariant means for ergodic group-actions. Ergod. Th. & Dynam. Sys. 1 (1981), 223–236.Google Scholar
Skandalis, G.. Une notion de nucléarité en K-théorie (d’après J. Cuntz). J. K-Theory 1 (1988), 549–573.Google Scholar
Takesaki, M.. Theory of operator algebras. II. Encyclopaedia of Mathematical Sciences. Vol. 125 (Operator Algebras and Non-commutative Geometry, 6) . Springer, Berlin, 2003.Google Scholar
Takesaki, M.. Theory of operator algebras. III. Encyclopaedia of Mathematical Sciences. Vol. 127 (Operator Algebras and Non-commutative Geometry, 8) . Springer, Berlin, 2003.Google Scholar
Vaes, S. and Verraedt, P.. Classification of type III Bernoulli crossed products. Adv. Math. 281 (2015), 296–332.Google Scholar
Vaes, S. and Wahl, J.. Bernoulli actions of type $\text{III}_{1}$ and $\text{L}^{2}$ -cohomology. Preprint, 2017, arXiv:1705.00439.Google Scholar
Zimmer, R.. Extensions of ergodic group actions. Illinois J. Math. 20 (1976), 373–409.Google Scholar
Zimmer, R.. Ergodic theory and semisimple groups. Monographs in Mathematics. Vol. 81. Birkhäuser, Basel, 1984.Google Scholar