Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-19T20:53:21.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Actions of symplectic homeomorphisms/diffeomorphisms on foliations by curves in dimension 2

Part of: Low-dimensional dynamical systems Finite-dimensional Hamiltonian, Lagrangian, contact, and nonholonomic systems

Published online by Cambridge University Press:  20 January 2022

MARIE-CLAUDE ARNAUD  and
MAXIME ZAVIDOVIQUE
MARIE-CLAUDE ARNAUD*
Affiliation:
Université de Paris and Sorbonne Université, CNRS, IMJ-PRG, F-75013 Paris, France
MAXIME ZAVIDOVIQUE
Affiliation:
Sorbonne Université and Université de Paris, CNRS, IMJ-PRG, F-75005 Paris, France (e-mail: maxime.zavidovique@upmc.fr)
*
e-mail: Marie-Claude.Arnaud@imj-prg.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The two main results in this paper concern the regularity of the invariant foliation of a 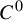$C^0$ -integrable symplectic twist diffeomorphism of the two-dimensional annulus, namely that (i) the generating function of such a foliation is 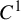$C^1$ , and (ii) the foliation is Hölder with exponent 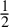$\tfrac 12$ . We also characterize foliations by graphs that are straightenable via a symplectic homeomorphism and prove that every symplectic homeomorphism that leaves invariant all the leaves of a straightenable foliation has Arnol’d–Liouville coordinates, in which the dynamics restricted to the leaves is conjugate to a rotation. We deduce that every Lipschitz integrable symplectic twist diffeomorphisms of the two-dimensional annulus has Arnol’d–Liouville coordinates and then provide examples of ‘strange’ Lipschitz foliations by smooth curves that cannot be straightened by a symplectic homeomorphism and cannot be invariant by a symplectic twist diffeomorphism.

Keywords

twist mapssymplectic homeomorphismsgenerating functionsintegrability

MSC classification

Primary: 37E40: Twist maps
Secondary: 37E10: Maps of the circle 37J30: Obstructions to integrability (nonintegrability criteria)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 3 , March 2023 , pp. 794 - 826
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnaud, M.-C.. Three results on the regularity of the curves that are invariant by an exact symplectic twist map. Publ. Math. Inst. Hautes Études Sci. 109 (2009), 1–17.CrossRefGoogle Scholar
Arnaud, M.-C.. Hyperbolicity for conservative twist maps of the 2-dimensional annulus, note of a course given in Salto. Publ. Mat. Urug. 16 (2016), 1–39.Google Scholar
Arnaud, M.-C. and Xue, J.. A ${C}^1$ Arnol’d–Liouville theorem. Quelques aspects de la théorie des systèmes dynamiques: un hommage à Jean–Christophe Yoccoz. II (Astérisque, 416). Eds. S. Crovisier, R. Krikorian, C. Matheus and S. Senti. Société Mathématique de France, Paris, 2020, pp. 1–31.Google Scholar
Birkhoff, G. D.. Surface transformations and their dynamical application. Acta Math. 43 (1920), 1–119.CrossRefGoogle Scholar
Cheng, J. and Sun, Y.. A necessary and sufficient condition for a twist map being integrable. Sci. China Ser. A 39(7) (1996), 709–717.Google Scholar
Duistermaat, J. J.. On global action-angle coordinates. Comm. Pure Appl. Math. 33(6) (1980), 687–706.CrossRefGoogle Scholar
Fathi, A.. Une interprétation plus topologique de la démonstration du théorème de Birkhoff. Sur les courbes invariantes par les difféomorphismes de l’anneau (Astérisque, 103–104). Société Mathématique de France, Paris, 1983. Appendix to Ch. 1, pp. 39–46.Google Scholar
Florio, A. and Le Calvez, P.. Torsion of instability zones for conservative twist maps of the annulus. Nonlinearity 34(1) (2021), 411–423.CrossRefGoogle Scholar
Greene, R. E. and Shiohama, K.. Diffeomorphisms and volume-preserving embeddings of noncompact manifolds. Trans. Amer. Math. Soc. 255 (1979), 403–414.CrossRefGoogle Scholar
Herman, M.. Sur les courbes invariantes par les difféomorphismes de l’anneau (Astérisque, 103–104). Société Mathématique de France, Paris, 1983.Google Scholar
Hirsch, M. W., Pugh, C. C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
Kolmogorov, A. and Fomine, S.. Eléments de la théorie des fonctions et de l’analyse fonctionnelle. Mir, Moscow, 1974 (in French). With an addendum on Banach algebra by V. M. Tikhomirov. Translated from Russian by Michel Dragnev.Google Scholar
Lefeuvre, T.. Uniform approximation of volume-preserving homeomorphisms by volume-preserving diffeomorphisms. Available at https://thibaultlefeuvre.files.wordpress.com/2016/04/volume_preserving1.pdf.Google Scholar
Mañé, R.. Ergodic Theory and Differentiable Dynamics (Ergebnisse der Mathematik und ihrer Grenzgebiete, 8). Springer-Verlag, Berlin, 1987, translated from the Portuguese by S. Levy.CrossRefGoogle Scholar
Massart, D. and Sorrentino, A.. Differentiability of Mather’s average action and integrability on closed surfaces. Nonlinearity 24(6) (2011), 1777–1793.CrossRefGoogle Scholar
Minguzzi, E.. The equality of mixed partial derivatives under weak differentiability conditions. Real Anal. Exchange 40(1) (2014/15), 81–97.CrossRefGoogle Scholar
Oh, Y.-G.. ${C}^0$ -coerciveness of Moser’s problem and smoothing area preserving homeomorphisms. Preprint, 2006, arXiv:math/0601183.Google Scholar
Oh, Y. G. and Müller, S.. The group of Hamiltonian homeomorphisms and ${C}^0$ -symplectic topology. J. Symplectic Geom. 5(2) (2007), 167–219.Google Scholar
Rudin, W.. Principles of Mathematical Analysis, 3rd edn. McGraw-Hill, New York, 1976.Google Scholar