Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-03T02:55:57.828Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost proximal extensions of minimal flows

Part of: Topological dynamics

Published online by Cambridge University Press:  16 January 2023

YANG CAO  and
SONG SHAO
YANG CAO
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, P. R. China (e-mail: cy412@mail.ustc.edu.cn)
SONG SHAO*
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, P. R. China (e-mail: cy412@mail.ustc.edu.cn)
*
e-mail: songshao@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study almost proximal extensions of minimal flows. Let 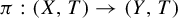$\pi : (X,T)\rightarrow (Y,T)$ be an extension of minimal flows. Then 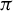$\pi $ is called an almost proximal extension if there is some 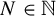$N\in {\mathbb N}$ such that the cardinality of any almost periodic subset in each fiber is not greater than N. When 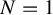$N=1$, 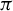$\pi $ is proximal. We will give the structure of 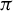$\pi $ and give a dichotomy theorem: any almost proximal extension of minimal flows is either almost finite to one, or almost all fibers contain an uncountable strongly scrambled subset. Using the category method, Glasner and Weiss showed the existence of proximal but not almost one-to-one extensions [On the construction of minimal skew products. Israel J. Math. 34 (1979), 321–336]. In this paper, we will give explicit such examples, and also examples of almost proximal but not almost finite to one extensions.

Keywords

proximal extensionsminimal flowschaosweak mixinguniform rigidity

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 37B20: Notions of recurrence
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 12 , December 2023 , pp. 4041 - 4073
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E., Auslander, J. and Glasner, E.. The topological dynamics of Ellis actions. Mem. Amer. Math. Soc. 195 (2008), Article no. 913.Google Scholar
Akin, E., Glasner, E., Huang, W., Shao, S. and Ye, X.. Sufficient conditions under which a transitive system is chaotic. Ergod. Th. & Dynam. Sys. 30 (2010), 1277–1310.CrossRefGoogle Scholar
Auslander, J.. Regular minimal sets. I. Trans. Amer. Math. Soc. 123 (1966), 469–479.CrossRefGoogle Scholar
Auslander, J.. Minimal Flows and their Extensions (North-Holland Mathematics Studies, 153). North-Holland, Amsterdam, 1988.Google Scholar
Auslander, J. and Glasner, S.. Distal and highly proximal extensions of minimal flows. Indiana Univ. Math. J. 26 (1977), 731–749.CrossRefGoogle Scholar
Auslander, J., McMahon, D., van der Woude, J. and Wu, T.. Weak disjointness and the equicontinuous structure relation. Ergod. Th. & Dynam. Sys. 4 (1984), 323–351.CrossRefGoogle Scholar
C̆iklová-Mlíchová, M.. Li–Yorke sensitive minimal maps. Nonlinearity 19 (2006), 517–529.CrossRefGoogle Scholar
de Vries, J.. Elements of Topological Dynamics. Kluwer Academic Publishers, Dordrecht, 1993.10.1007/978-94-015-8171-4CrossRefGoogle Scholar
Ellis, D., Ellis, R. and Nerurkar, M.. The topological dynamics of semigroup actions. Trans. Amer. Math. Soc. 353 (2001), 1279–1320.10.1090/S0002-9947-00-02704-5CrossRefGoogle Scholar
Ellis, R.. Lectures on Topological Dynamics. W. A. Benjamin, Inc., New York, 1969.Google Scholar
Ellis, R., Glasner, S. and Shapiro, L.. Proximal-isometric flows. Adv. Math. 17 (1975), 213–260.CrossRefGoogle Scholar
Ellis, R. and Gottschalk, W.. Homomorphisms of transformation groups. Trans. Amer. Math. Soc. 94 (1960), 258–271.CrossRefGoogle Scholar
Furstenberg, H.. The structure of distal flows. Amer. J. Math. 85 (1963), 477–515.CrossRefGoogle Scholar
Furstenberg, H. and Weiss, B.. On almost $1$ - $1$ extensions. Israel J. Math. 65 (1989), 311–322.CrossRefGoogle Scholar
Glasner, E.. Regular PI metric flows are equicontinuous. Proc. Amer. Math. Soc. 114 (1992), 269–277.CrossRefGoogle Scholar
Glasner, E.. Topological weak mixing and quasi-Bohr systems. Israel J. Math. 148 (2005), 277–304.CrossRefGoogle Scholar
Glasner, S.. Proximal Flows (Lecture Notes in Mathematics, 517). Springer-Verlag, Berlin, 1976.CrossRefGoogle Scholar
Glasner, S. and Maon, D.. Rigidity in topological dynamics. Ergod. Th. & Dynam. Sys. 9 (1989), 309–320.CrossRefGoogle Scholar
Glasner, S. and Weiss, B.. On the construction of minimal skew products. Israel J. Math. 34 (1979), 321–336.CrossRefGoogle Scholar
Huang, W., Lian, Z., Shao, S. and Ye, X.. Minimal systems with finitely many ergodic measures. J. Funct. Anal. 280(12) (2021), Paper no. 109000.10.1016/j.jfa.2021.109000CrossRefGoogle Scholar
McMahon, D. C.. Weak mixing and a note on a structure theorem for minimal transformation groups. Illinois J. Math. 20(2) (1976), 186–197.CrossRefGoogle Scholar
Rees, M.. A point distal transformation of the torus. Israel J. Math. 32 (1979), 201–208.CrossRefGoogle Scholar
Shao, S. and Ye, X.. A non-PI minimal system is Li–Yorke sensitive. Proc. Amer. Math. Soc. 146 (2018), 1105–1112.CrossRefGoogle Scholar
Shoenfeld, P.. Highly proximal and generalized almost finite extensions of minimal sets. Pacific J. Math. 66 (1976), 265–280.10.2140/pjm.1976.66.265CrossRefGoogle Scholar
Smítal, J.. Why it is important to understand dynamics of triangular maps? J. Difference Equ. Appl. 14 (2008), 597–606.CrossRefGoogle Scholar
van der Woude, J.. Topological dynamics. Dissertation, Vrije Universiteit, Amsterdam, 1982. CWI Tract, 22.Google Scholar
Veech, W. A.. Point-distal flows. Amer. J. Math. 92 (1970), 205–242.CrossRefGoogle Scholar
Veech, W. A.. Topological systems. Bull. Amer. Math. Soc. (N.S.) 83 (1977), 775–830.CrossRefGoogle Scholar
Zhang, G.. Relative entropy, asymptotic pairs and chaos. J. Lond. Math. Soc. (2) 73 (2006), 157–172.CrossRefGoogle Scholar