Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-08T02:26:30.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Equilibrium stability for non-uniformly hyperbolic systems

Published online by Cambridge University Press:  18 January 2018

JOSÉ F. ALVES ,
VANESSA RAMOS  and
JAQUELINE SIQUEIRA
JOSÉ F. ALVES
Affiliation:
Centro de Matemática da Universidade do Porto, Rua do Campo Alegre 687, 4169-007 Porto, Portugal email jfalves@fc.up.pt
VANESSA RAMOS
Affiliation:
Centro de Ciências Exatas e Tecnologia-UFMA, Av. dos Portugueses, 1966, Bacanga, 65080-805 São Luís, Brazil email vramos@impa.br
JAQUELINE SIQUEIRA
Affiliation:
Departamento de Matemática PUC-Rio, Marquês de Sâo Vicente 225, Gávea, 225453-900 Rio de Janeiro, Brazil email jaqueline@mat.puc-rio.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for a wide family of non-uniformly hyperbolic maps and hyperbolic potentials we have equilibrium stability, i.e. the equilibrium states depend continuously on the dynamics and the potential. For this we deduce that the topological pressure is continuous as a function of the dynamics and the potential. We also prove the existence of finitely many ergodic equilibrium states for non-uniformly hyperbolic skew products and hyperbolic Hölder continuous potentials. Finally, we show that these equilibrium states vary continuously in the 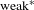$\text{weak}^{\ast }$ topology within such systems.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 10 , October 2019 , pp. 2619 - 2642
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, J. F.. SRB measures for non-hyperbolic systems with multidimensional expansion. Ann. Sci. Éc. Norm. Supér. (4) 33 (2000), 1–32.Google Scholar
Alves, J. F., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398.Google Scholar
Alves, J. F. and Viana, M.. Statistical stability for robust classes of maps with non-uniform expansion. Ergod. Th. & Dynam. Sys. 22 (2002), 1–32.Google Scholar
Andronov, A. and Pontryagin, L.. Systèmes grossiers. Dokl. Akad. Nauk USSR 14 (1937), 247–251.Google Scholar
Araújo, V.. Semicontinuity of entropy, existence of equilibrium states and continuity of physical measures. Discrete Contin. Dyn. Syst. 17(2) (2007), 371–386.Google Scholar
Arbieto, A., Matheus, C. and Oliveira, K.. Equilibrium states for random non-uniformly expanding maps. Nonlinearity 17 (2004), 581–593.Google Scholar
Bomfim, T., Castro, A. and Varandas, P.. Differentiability of thermodynamical quantities in non-uniformly expanding dynamics. Adv. Math. 292 (2016), 478–528.Google Scholar
Bowen, R.. Entropy for group endomorphisms and homogeneous spaces. Trans. Amer. Math. Soc. 153 (1971), 401–414.Google Scholar
Buzzi, J., Fisher, T., Sambarino, M. and Vásquez, C.. Maximal entropy measures for certain partially hyperbolic, derived from Anosov systems. Ergod. Th. & Dynam. Sys. 32 (2011), 63–79.Google Scholar
Buzzi, J., Paccaut, F. and Schmitt, B.. Conformal measures for multidimensional piecewise invertible maps. Ergod. Th. & Dynam. Sys. 21 (2001), 1035–1049.Google Scholar
Buzzi, J. and Sarig, O.. Uniqueness of equilibrium measures for countable Markov shifts. Ergod. Th. & Dynam. Sys. 23 (2003), 1383–1400.Google Scholar
Castro, A. and Nascimento, T.. Statistical properties of the maximal entropy measure for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 37 (2017), 1060–1101.Google Scholar
Castro, A. and Varandas, P.. Equilibrium states for non-uniformly expanding maps: decay of correlations and strong stability. Ann. Inst. H. Poincaré Anal. Non Linéaire 30(2) (2013), 225–249.Google Scholar
Climenhaga, V., Fisher, T. and Thompson, D. J.. Unique equilibrium states for Bonatti–Viana diffeomorphisms. Preprint, 2016.Google Scholar
Climenhaga, V., Fisher, T. and Thompson, D. J.. Equilibrium states for Mañé diffeomorphisms. Ergod. Th. & Dynam. Sys., accepted.Google Scholar
Deimling, K.. Nonlinear Functional Analysis. Springer, Berlin, 1985.Google Scholar
Díaz, L. J., Horita, V., Rios, I. and Sambarino, M.. Destroying horseshoes via heterodimensional cycles: generating bifurcations inside homoclinic classes. Ergod. Th. & Dynam. Sys. 29 (2009), 433–474.Google Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. (2) 16 (1977), 568–576.Google Scholar
Leplaideur, R., Oliveira, K. and Rios, I.. Equilibrium states for partially hyperbolic horseshoes. Ergod. Th. & Dynam. Sys. 31 (2011), 179–195.Google Scholar
Oliveira, K. and Viana, M.. Thermodynamical formalism for robust classes of potentials and non-uniformly hyperbolic maps. Ergod. Th. & Dynam. Sys. 28 (2008), 501–533.Google Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems: Contemporary Views and Applications (Chicago Lectures in Mathematics) . University of Chicago Press, Chicago, IL, 1997.Google Scholar
Ramos, V. and Siqueira, J.. On equilibrium states for partially hyperbolic horseshoes: uniqueness and statistical properties. Bull. Braz. Math. Soc. (N.S.) 48 (2017), 347–375.Google Scholar
Ramos, V. and Viana, M.. Equilibrium states for hyperbolic potentials. Nonlinearity 30 (2017), 825–847.Google Scholar
Rios, I. and Siqueira, J.. On equilibrium states for partially hyperbolic horseshoes. Ergod. Th. & Dynam. Sys. 21 (2016), 1–35.Google Scholar
Ruelle, D.. Statistical mechanics of a one-dimensional lattice gas. Commun. Math. Phys. 9(4) (1968), 267–278.Google Scholar
Ruelle, D.. Thermodynamic Formalism (Encyclopedia Mathematics and its Applications, 5) . Addison-Wesley, Reading, MA, 1978.Google Scholar
Sarig, O.. Thermodynamic formalism for countable Markov shifts. Ergod. Th. & Dynam. Sys. 19 (1999), 1565–1593.Google Scholar
Sarig, O.. Existence of Gibbs measures for countable Markov shifts. Proc. Amer. Math. Soc. 131 (2003), 1751–1758.Google Scholar
Sinai, Y.. Gibbs measures in ergodic theory. Russian Math. Surveys 27 (1972), 21–69.Google Scholar
Varandas, P. and Viana, M.. Existence, uniqueness and stability of equilibrium states for non-hyperbolic expanding maps. Ann. Inst. H. Poincaré Anal. Non Linéaire 27 (2010), 555–593.Google Scholar
Viana, M. and Oliveira, K. Foundations of Ergodic Theory (Cambridge Studies in Advanced Mathematics, 151) . Cambridge University Press, Cambridge, 2016.Google Scholar
Walters, P.. A variational principle for the pressure of continuous transformations. Amer. J. Math. 97 (1975), 937–997.Google Scholar