Hostname: page-component-77c89778f8-cnmwb Total loading time: 0 Render date: 2024-07-19T05:11:11.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Fatou components with punctured limit sets

Published online by Cambridge University Press:  23 April 2014

LUKA BOC-THALER ,
JOHN ERIK FORNÆSS  and
HAN PETERS
LUKA BOC-THALER
Affiliation:
Faculty of Mathematics and Physics, Institute of Mathematics, Physics and Mechanics, University of Ljubljana, Jadranska 19, 1000 Ljubljana, Slovenia email luka.boc@imfm.si
JOHN ERIK FORNÆSS
Affiliation:
Department of Mathematical Sciences, Norwegian University of Science and Technology, 7491 Trondheim, Norway email john.fornass@math.ntnu.no
HAN PETERS
Affiliation:
Korteweg de Vries Institute for Mathematics, University of Amsterdam, PO Box 94248, 1090 GE Amsterdam, The Netherlands email h.peters@uva.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

We study invariant Fatou components for holomorphic endomorphisms in 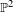$\mathbb{P}^{2}$. In the recurrent case these components were classified by Fornæss and Sibony [Classification of recurrent domains for some holomorphic maps. Math. Ann. 301(4) (1995), 813–820]. Ueda [Holomorphic maps on projective spaces and continuations of Fatou maps. Michigan Math J.56(1) (2008), 145–153] completed this classification by proving that it is not possible for the limit set to be a punctured disk. Recently Lyubich and Peters [Classification of invariant Fatou components for dissipative Hénon maps. Preprint] classified non-recurrent invariant Fatou components, under the additional hypothesis that the limit set is unique. Again all possibilities in this classification were known to occur, except for the punctured disk. Here we show that the punctured disk can indeed occur as the limit set of a non-recurrent Fatou component. We provide many additional examples of holomorphic and polynomial endomorphisms of 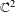$\mathbb{C}^{2}$ with non-recurrent Fatou components on which the orbits converge to the regular part of arbitrary analytic sets.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1380 - 1393
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, M., Bracci, F. and Tovena, F.. Embeddings of submanifolds and normal bundles. Adv. Math. 220(2) (2009), 620–656.CrossRefGoogle Scholar
Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of ℂ2: currents, equilibrium measure and hyperbolicity. Invent. Math. 103(1) (1991), 69–99.CrossRefGoogle Scholar
Bracci, F. and Zaitsev, D.. Dynamics of one-resonant biholomorphisms. J. Eur. Math. Soc. (JEMS) 15(1) (2013), 179–200.Google Scholar
Brochero Martínez, F. E.. Groups of germs of analytic diffeomorphisms in (ℂ2, 0). J. Dyn. Control Syst. 9(1) (2003), 1–32.CrossRefGoogle Scholar
Chirka, E. M.. Complex Analytic Sets (Mathematics and its Applications (Soviet Series), 46). Kluwer Academic, Dordrecht, 1989. Translated from the Russian by R. A. M. Hoksbergen.Google Scholar
Fornæss, J. E. and Sibony, N.. Complex dynamics in higher dimension. I. Asterisque 222 (1991), 201–231.Google Scholar
Fornæss, J. E. and Sibony, N.. Classification of recurrent domains for some holomorphic maps. Math. Ann. 301(4) (1995), 813–820.CrossRefGoogle Scholar
Fornæss, J.-E. and Sibony, N.. Complex dynamics in higher dimension II. Modern Methods in Complex Analysis (Annals of Mathematics Studies, 137). Princeton University Press, Princeton, NJ, 1995, pp. 135–182.Google Scholar
Forster, O.. Lectures on Riemann Surfaces (Graduate Texts in Mathematics, 81). Springer, New York, 1991, Translated from the 1977 German original by Bruce Gilligan. Reprint of the 1981 English translation.Google Scholar
Forstnerič, F.. Stein manifolds and holomorphic mappings. The Homotopy Principle in Complex Analysis (Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge, A Series of Modern Surveys in Mathematics, 56). Springer, Berlin, 2011.Google Scholar
Grauert, H. and Remmert, R.. Theorie der Steinschen Raume (Grundlehren der mathematischen Wissenschaften, 227). Springer, Berlin, 1977.CrossRefGoogle Scholar
Hakim, M.. Analytic transformations of (ℂp, 0) tangent to the identity. Duke Math. J. 92 (1998), 403–428.CrossRefGoogle Scholar
Hubbard, J. H. and Papadopol, P.. Superattractive fixed points in ℂn. Indiana Univ. Math. J. 43 (1994), 321–365.CrossRefGoogle Scholar
Jupiter, D. and Lilov, K.. Invariant Fatou components of automorphisms of ℂ2. Far East J. Dyn. Syst. 6(1) (2003), 49–65.Google Scholar
Krantz, S. G.. Function Theory of Several Complex Variables. AMS Chelsea Publishing, Providence, RI, 2001, Reprint of the 1992 edition.CrossRefGoogle Scholar
Lyubich, M. and Peters, H.. Classification of invariant Fatou components for dissipative Hénon maps. IMS Preprint 12-07.Google Scholar
Narasimhan, R.. Introduction to the Theory of Analytic Spaces (Lecture Notes in Mathematics, 25). Springer, Berlin, 1966.CrossRefGoogle Scholar
Sullivan, D.. Quasiconformal homeomorphisms and dynamics. I. Solution of the Fatou–Julia problem on wandering domains. Ann. of Math. 122 (1985), 401–418.CrossRefGoogle Scholar
Ueda, T.. Fatou sets in complex dynamics on projective spaces. J. Math. Soc. Japan 46 (1994), 545–555.CrossRefGoogle Scholar
Ueda, T.. Holomorphic maps on projective spaces and continuations of Fatou maps. Michigan Math J. 56(1) (2008), 145–153.CrossRefGoogle Scholar
Weickert, B. J.. Nonwandering, nonrecurrent Fatou components in ℙ2. Pacific J. Math. 211(2) (2003), 391–397.CrossRefGoogle Scholar