No CrossRef data available.
Article contents
A fixed-point curve theorem for finite-orbits local diffeomorphisms
Part of:
Complex dynamical systems
Differential equations in the complex domain
Smooth dynamical systems: general theory
Holomorphic mappings and correspondences
Published online by Cambridge University Press: 16 February 2023
Abstract
We study local biholomorphisms with finite orbits in some neighborhood of the origin since they are intimately related to holomorphic foliations with closed leaves. We describe the structure of the set of periodic points in dimension 2. As a consequence we show that given a finite-orbits local biholomorphism F, in dimension 2, there exists an analytic curve passing through the origin and contained in the fixed-point set of some non-trivial iterate of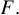 
$F.$ As an application we obtain that at least one eigenvalue of the linear part of F at the origin is a root of unity. Moreover, we show that such a result is sharp by exhibiting examples of finite-orbits local biholomorphisms such that exactly one of the eigenvalues is a root of unity. These examples are subtle since we show they cannot be embedded in one-parameter groups.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
Abate, M.. The residual index and the dynamics of holomorphic maps tangent to the identity. Duke Math. J. 107(1) (2001), 173–207.10.1215/S0012-7094-01-10719-9CrossRefGoogle Scholar
Bierstone, E. and Milman, P. D.. Semianalytic and subanalytic sets. Publ. Math. Inst. Hautes Études Sci. 67 (1988), 5–42.CrossRefGoogle Scholar
Brochero Martínez, F. E., Cano, F. and López-Hernanz, L.. Parabolic curves for diffeomorphisms in
${\mathbb{C}}^2$
. Publ. Mat. 52(1) (2008), 189–194.CrossRefGoogle Scholar
${\mathbb{C}}^2$
. Publ. Mat. 52(1) (2008), 189–194.CrossRefGoogle ScholarBryuno, A. D.. Analytical form of differential equations. Trans. Moscow Math. Soc. 25 (1973), 131–288.Google Scholar
Camacho, C. and Sad, P.. Invariant varieties through singularities of holomorphic vector fields. Ann. of Math. (2) 115(3) (1982), 579–595.CrossRefGoogle Scholar
Câmara, L. and Scárdua, B.. On the integrability of holomorphic vector fields. Discrete Contin. Dyn. Syst. 25(2) (2009), 481–493.CrossRefGoogle Scholar
Carrillo, S. A. and Sanz, F.. Briot–Bouquet’s theorem in high dimension. Publ. Mat. 58 (2014), 135–152.CrossRefGoogle Scholar
Câmara, L. and Scárdua, B.. Periodic complex map germs and foliations. An. Acad. Brasil. Ciênc. 89(4) (2017), 2563–2579.CrossRefGoogle ScholarPubMed
Écalle, J.. Théorie itérative: introduction à la théorie des invariants holomorphes. J. Math. Pures Appl. (9) 54 (1975), 183–258.Google Scholar
Edwards, R., Millett, K. and Sullivan, D.. Foliations with all leaves compact. Topology 16 (1977), 13–32.CrossRefGoogle Scholar
Engelking, R.. General Topology (Sigma Series in Pure Mathematics, 6), 2nd edn. Heldermann Verlag, Berlin, 1989. Translated from the Polish by the author.Google Scholar
Ilyashenko, Y. and Yakovenko, S.. Lectures on Analytic Differential Equations (Graduate Studies in Mathematics, 86). American Mathematical Society, Providence, RI, 2008.Google Scholar
López-Hernanz, L., Raissy, J., Ribón, J. and Sanz-Sánchez, F.. Stable manifolds of two-dimensional biholomorphisms asymptotic to formal curves. Int. Math. Res. Not. IMRN 2021(17) (2021), 12847–12887.CrossRefGoogle Scholar
López-Hernanz, L., Ribón, J., Sanz-Sánchez, F. and Vivas, L.. Stable manifolds of biholomorphisms in
${\mathbb{C}}^n$
asymptotic to formal curves. Proc. Lond. Math. Soc. (3) 125 (2022), 277–317; doi:10.1112/plms.12447.CrossRefGoogle Scholar
${\mathbb{C}}^n$
asymptotic to formal curves. Proc. Lond. Math. Soc. (3) 125 (2022), 277–317; doi:10.1112/plms.12447.CrossRefGoogle ScholarLojasiewicz, S.. Triangulation of semi-analytic sets. Ann. Sc. Norm. Super. Pisa Cl. Sci. (3) 18(4) (1964), 449–474.Google Scholar
López-Hernanz, L. and Sánchez, F. S.. Parabolic curves of diffeomorphisms asymptotic to formal invariant curves. J. Reine Angew. Math. 739 (2018), 277–296.10.1515/crelle-2015-0064CrossRefGoogle Scholar
Martinet, J.. Normalisation des champs de vecteurs holomorphes. Séminaire Bourbaki: vol. 1980/81, Exposés 561–578 (Séminaire Bourbaki, 23). Eds. A. Dold and B. Eckmann. Springer-Verlag, Berlin, 1981, pp. 55–70.CrossRefGoogle Scholar
Mattei, J.-F. and Moussu, R.. Holonomie et intégrales premières. Ann. Sci. Éc. Norm. Supér. (4) 13(4) (1980), 469–523.CrossRefGoogle Scholar
Martinet, J. and Ramis, J.-P.. Classification analytique des équations differentielles non linéaires résonnantes du premier ordre. Ann. Sci. Éc. Norm. Supér. (4) 4(16) (1983), 571–621.CrossRefGoogle Scholar
Nadler, S. B. Jr. Continuum Theory. An Introduction (Pure and Applied Mathematics, 158). Marcel Dekker, New York, 1992.Google Scholar
Pöschel, J.. On invariant manifolds of complex analytic mappings near fixed points. Expo. Math. 4 (1986), 97–109.Google Scholar
Pérez-Marco, R.. Fixed points and circle maps. Acta Math. 179(2) (1997), 243–294.CrossRefGoogle Scholar
Ribón, J.. Families of diffeomorphisms without periodic curves. Michigan Math. J. 53(2) (2005), 243–256.CrossRefGoogle Scholar
Rebelo, J. C. and Reis, H.. A note on integrability and finite orbits for subgroups of
$\mathrm{Diff}\left({\mathbb{C}}^n,0\right)$
. Bull. Braz. Math. Soc. (N.S.) 46(3) (2015), 469–490.10.1007/s00574-015-0101-2CrossRefGoogle Scholar
$\mathrm{Diff}\left({\mathbb{C}}^n,0\right)$
. Bull. Braz. Math. Soc. (N.S.) 46(3) (2015), 469–490.10.1007/s00574-015-0101-2CrossRefGoogle ScholarRuelle, D.. Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press, Boston, MA, 1989.Google Scholar