No CrossRef data available.
Article contents
Horseshoes and Lyapunov exponents for Banach cocycles over non-uniformly hyperbolic systems
Part of:
Normed linear spaces and Banach spaces; Banach lattices
Dynamical systems with hyperbolic behavior
Ergodic theory
Published online by Cambridge University Press: 27 February 2023
Abstract
We extend Katok’s result on ‘the approximation of hyperbolic measures by horseshoes’ to Banach cocycles. More precisely, let f be a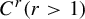 
$C^r(r>1)$ diffeomorphism of a compact Riemannian manifold M, preserving an ergodic hyperbolic measure 
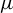$\mu $ with positive entropy, and let 
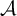$\mathcal {A}$ be a Hölder continuous cocycle of bounded linear operators acting on a Banach space 
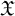$\mathfrak {X}$. We prove that there is a sequence of horseshoes for f and dominated splittings for 
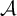$\mathcal {A}$ on the horseshoes, such that not only the measure theoretic entropy of f but also the Lyapunov exponents of 
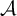$\mathcal {A}$ with respect to 
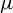$\mu $ can be approximated by the topological entropy of f and the Lyapunov exponents of 
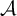$\mathcal {A}$ on the horseshoes, respectively. As an application, we show the continuity of sub-additive topological pressure for Banach cocycles.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
Avila, A., Crovisier, S. and Wilkinson, A..
${C}^1$
density of stable ergodicity. Adv. Math. 379 (2021), 107496.10.1016/j.aim.2020.107496CrossRefGoogle Scholar
${C}^1$
density of stable ergodicity. Adv. Math. 379 (2021), 107496.10.1016/j.aim.2020.107496CrossRefGoogle ScholarBan, J., Cao, Y. and Hu, H.. The dimensions of a non-conformal repeller and an average conformal repeller. Trans. Amer. Math. Soc. 362(2) (2010), 727–751.10.1090/S0002-9947-09-04922-8CrossRefGoogle Scholar
Barreira, L. and Pesin, Y.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and its Applications, 115). Cambridge University Press, Cambridge, 2007.10.1017/CBO9781107326026CrossRefGoogle Scholar
Blumenthal, A. and Morris, I. D.. Characterization of dominated splittings for operator cocycles acting on Banach spaces. J. Differential Equations 267(7) (2019), 3977–4013.10.1016/j.jde.2019.04.033CrossRefGoogle Scholar
Cao, Y., Feng, D. and Huang, W.. The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20(3) (2008), 639–657.10.3934/dcds.2008.20.639CrossRefGoogle Scholar
Cao, Y., Luzzatto, S. and Rios, I.. The boundary of hyperbolicity for Hénon-like families. Ergod. Th. & Dynam. Sys. 28 (2008), 1049–1080.10.1017/S0143385707000776CrossRefGoogle Scholar
Cao, Y., Pesin, Y. and Zhao, Y.. Dimension estimates of non-conformal repellers and continuity of sub-additive topological pressure. Geom. Funct. Anal. 29(5) (2019), 1325–1368.10.1007/s00039-019-00510-7CrossRefGoogle Scholar
Chung, Y. M.. Shadowing properties of non-invertible maps with hyperbolic measures. Tokyo J. Math. 22 (1999), 145–166.10.3836/tjm/1270041619CrossRefGoogle Scholar
Froyland, G., Lloyd, S. and Quas, A.. Coherent structures and isolated spectrum for Perron–Frobenius cocycles. Ergod. Th. & Dynam. Sys. 30(3) (2010), 729–756.10.1017/S0143385709000339CrossRefGoogle Scholar
Froyland, G., Lloyd, S. and Quas, A.. A semi-invertible Oseledets theorem with applications to transfer operator cocycles. Discrete Contin. Dyn. Syst. 33(9) (2013), 3835–3860.CrossRefGoogle Scholar
Gelfert, K.. Repellers for non-uniformly expanding maps with singular or critical points. Bull. Braz. Math. Soc. (N.S.) 41(2) (2010), 237–257.10.1007/s00574-010-0012-1CrossRefGoogle Scholar
Gelfert, K.. Horseshoes for diffeomorphisms preserving hyperbolic measures. Math. Z. 283(3–4) (2016), 685–701.10.1007/s00209-016-1618-9CrossRefGoogle Scholar
González-Tokman, C. and Quas, A.. A concise proof of the multiplicative ergodic theorem on Banach spaces. J. Mod. Dyn. 9 (2015), 237–255.10.3934/jmd.2015.9.237CrossRefGoogle Scholar
Kalinin, B. and Sadovskaya, V.. Periodic approximation of Lyapunov exponents for Banach cocycles. Ergod. Th. & Dynam. Sys. 39(3) (2019), 689–706.10.1017/etds.2017.43CrossRefGoogle Scholar
Kato, T.. Perturbation Theory for Linear Operators (Classics in Mathematics, 132). Springer-Verlag, Berlin, 1995, reprint of the 1980 edition.10.1007/978-3-642-66282-9CrossRefGoogle Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, Cambridge, 1995.10.1017/CBO9780511809187CrossRefGoogle Scholar
Lian, Z. and Lu, K.. Lyapunov exponents and invariant manifolds for random dynamical systems in a Banach space. Mem. Amer. Math. Soc. 206(967) (2010), vi+106 pp.Google Scholar
Lian, Z. and Ma, X.. Existence of periodic orbits and horseshoes for mappings in a separable Banach space. J. Differential Equations 269(12) (2020), 11694–11738.10.1016/j.jde.2020.08.004CrossRefGoogle Scholar
Lian, Z. and Young, L.-S.. Lyapunov exponents, periodic orbits and horseshoes for mappings of Hilbert spaces. Ann. Henri Poincaré 12(6) (2011), 1081–1108.10.1007/s00023-011-0100-9CrossRefGoogle Scholar
Lian, Z. and Young, L.-S.. Lyapunov exponents, periodic orbits, and horseshoes for semiflows on Hilbert spaces. J. Amer. Math. Soc. 25(3) (2012), 637–665.10.1090/S0894-0347-2012-00734-6CrossRefGoogle Scholar
Mañé, R.. Lyapunov exponents and stable manifolds for compact transformations. Geometric Dynamics (Proceedings of the International Symposium, held at the Instituto de Matematica Pura e Aplicada, Rio de Janeiro, Brasil, July–August 1981) (Lecture Notes in Mathematics, 1007). Ed. J. Palis. Springer, Berlin, 1983, pp. 522–577.Google Scholar
Mendoza, L.. Ergodic attractors for diffeomorphisms of surfaces. J. Lond. Math. Soc. (2) 37(2) (1988), 362–374.10.1112/jlms/s2-37.2.362CrossRefGoogle Scholar
Oseledec, V. I.. A multiplicative ergodic theorem. Characteristic Ljapunov, exponents of dynamical systems. Tr. Moskov. Mat. Obšč. 19 (1968), 179–210.Google Scholar
Pesin, Y.. Families of invariant manifolds that correspond to nonzero characteristic exponents. Izv. Akad. Nauk SSSR Ser. Mat. 40(6) (1976), 1332–1379, 1440.Google Scholar
Quas, A., Thieullen, P. and Zarrabi, M.. Explicit bounds for separation between Oseledets subspaces. Dyn. Syst. 34(3) (2019), 517–560.10.1080/14689367.2019.1571562CrossRefGoogle Scholar
Rios, I.. Unfolding homoclinic tangencies inside horseshoes: Hyperbolicity, fractal dimensions and persistent tangencies. Nonlinearity 14 (2001), 431.10.1088/0951-7715/14/3/302CrossRefGoogle Scholar
Thieullen, P.. Fibrés dynamiques asymptotiquement compacts. Exposants de Lyapounov. Entropie. Dimension. Ann. Inst. H. Poincaré Anal. Non Linéaire 4(1) (1987), 49–97.10.1016/s0294-1449(16)30373-0CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer-Verlag, New York, 1982.10.1007/978-1-4612-5775-2CrossRefGoogle Scholar
Wang, J., Cao, Y. and Zou, R.. The approximation of uniform hyperbolicity for
${C}_1$
diffeomorphisms with hyperbolic measures. J. Differential Equations 275 (2021), 359–390.Google Scholar
${C}_1$
diffeomorphisms with hyperbolic measures. J. Differential Equations 275 (2021), 359–390.Google ScholarYang, Y.. Horseshoes for
${C}^{1+\alpha }$
mappings with hyperbolic measures. Discrete Contin. Dyn. Syst. 35(10) (2015), 5133–5152.10.3934/dcds.2015.35.5133CrossRefGoogle Scholar
${C}^{1+\alpha }$
mappings with hyperbolic measures. Discrete Contin. Dyn. Syst. 35(10) (2015), 5133–5152.10.3934/dcds.2015.35.5133CrossRefGoogle ScholarZhang, Y.. Dynamical upper bounds for Hausdorff dimension of invariant sets. Ergod. Th. & Dynam. Sys. 17(3) (1997), 739–756.CrossRefGoogle Scholar