Hostname: page-component-7479d7b7d-m9pkr Total loading time: 0 Render date: 2024-07-11T06:39:56.303Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-integrability of the 1:1:2–resonance

Published online by Cambridge University Press:  19 September 2008

J. J. Duistermaat
J. J. Duistermaat
Affiliation:
Mathematisch instituut, Rijksuniversiteit Utrecht, Budapestlaan 6, Postbus 80.010, 3508 TA Utrecht, The Netherlands
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

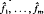A Hamiltonian system of n degrees of freedom, defined by the function F, with an equilibrium point at the origin, is called formally integrable if there exist A A formal power series , functionally independent, in involution, and such that the Taylor expansion 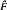of F is a formal power series in the .

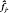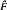Take n = 3, , F(k) homogeneous of degree k, F(2) > 0 and the eigenfrequencies in ratio 1:1:2. If F(3) avoids a certain hypersurface of ‘symmetric’ third order terms, then the F system is not formally integrable. If F(3) is symmetric but F(4) is in a non-void open subset, then homoclinic intersection with Devaney spiralling occurs; the angle decays of order 1 when approaching the origin.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 4 , Issue 4 , December 1984 , pp. 553 - 568
Copyright
Copyright © Cambridge University Press 1984

References

REFERENCES

[1]van der Aa, E. & Sanders, J.. The 1:2:1-resonance, its periodic orbits and integrals. Asymptotic Analysis, Springer Lecture Notes in Math. (Verhulst, , ed.) 711 (1979).Google Scholar
[2]Abraham, R. & Marsden, J. E.. Foundations of Mechanics, 2nd ed.Benjamin/Cummings, 1978.Google Scholar
[3]Devaney, R. L.. Homoclinic orbits in Hamiltonian systems. J. Diff. Eq. 21 (1976), 431–438.CrossRefGoogle Scholar
[4]Hánon, M. & Heiles, C.. The applicability of the third integral of motion: some numerical experiments. Astronom. J. 69 (1964), 73–79.Google Scholar
[5]Melnikov, V. K.. On the stability of the center for time periodic solutions. Trans. Moscow Math. Soc. 12 (1963), 3–56.Google Scholar
[6]Nilsson, N.. Some growth and ramification properties of certain integrals on algebraic manifolds. Ark. Mat. 5 (1965), 436–475.CrossRefGoogle Scholar
[7]Verhulst, F.. Asymptotic analysis in hamiltonian systems. Asymptotic Analysis II, Springer Lecture Notes in Math. 985 (1983), 137–193.Google Scholar
[8]Ziglin, S. L.. Branching of solutions and nonexistence of first integrals in Hamiltonian mechanics I. Fund. Anal, and its Appl. 16 (1982), 181–189; II, idem 17 (1983), 6–17.CrossRefGoogle Scholar