Hostname: page-component-7bb8b95d7b-cx56b Total loading time: 0 Render date: 2024-09-17T16:21:00.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal amenable subgroups of the automorphism group of sofic shifts

Part of: Topological dynamics

Published online by Cambridge University Press:  10 February 2020

KITTY YANG
KITTY YANG*
Affiliation:
Department of Mathematics, Northwestern University, Evanston, IL60208, USA email kyang@math.northwestern.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $(X,\unicode[STIX]{x1D70E})$ be a transitive sofic shift and let 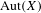$\operatorname{Aut}(X)$ denote its automorphism group. We generalize a result of Frisch, Schlank, and Tamuz to show that any normal amenable subgroup of 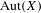$\operatorname{Aut}(X)$ must be contained in the subgroup generated by the shift. We also show that the result does not extend to higher dimensions by giving an example of a two-dimensional mixing shift of finite type due to Hochman whose automorphism group is amenable and not generated by the shift maps.

Keywords

symbolic dynamicssofic shiftshift of finite type

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 37B15: Cellular automata
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 4 , April 2021 , pp. 1250 - 1263
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. L. and Marcus, B.. Topological entropy and equivalence of dynamical systems. Mem. Amer. Math. Soc. 20(219) (1979).Google Scholar
Boyle, M.. Lower entropy factors of sofic systems. Ergod. Th. & Dynam. Sys. 3(4) (1983), 541–557.10.1017/S0143385700002133CrossRefGoogle Scholar
Boyle, M. and Krieger, W.. Periodic points and automorphisms of the shift. Trans. Amer. Math. Soc. 302(1) (1987), 125–149.10.1090/S0002-9947-1987-0887501-5CrossRefGoogle Scholar
Boyle, M., Lind, D. and Rudolph, D.. The automorphism group of a shift of finite type. Trans. Amer. Math. Soc. 306(1) (1988), 71–114.CrossRefGoogle Scholar
Ehrenfeucht, A. and Silberger, D. M.. Periodicity and unbordered segments of words. Discrete Math. 26(2) (1979), 101–109.10.1016/0012-365X(79)90116-XCrossRefGoogle Scholar
Frisch, J., Schlank, T. and Tamuz, O.. Normal amenable subgroups of the automorphism group of the full shift. Ergod. Th. & Dynam. Sys. 39(5) (2019), 1290–1298.CrossRefGoogle Scholar
Furman, A.. On minimal strongly proximal actions of locally compact groups. Israel J. Math. 136 (2003), 173–187.10.1007/BF02807197CrossRefGoogle Scholar
Glasner, S.. Topological dynamics and group theory. Trans. Amer. Math. Soc. 187 (1974), 327–334.10.1090/S0002-9947-1974-0336723-1CrossRefGoogle Scholar
Glasner, S.. Proximal Flows (Lecture Notes in Mathematics, 517) . Springer, New York, 1976.10.1007/BFb0080139CrossRefGoogle Scholar
Hedlund, G. A.. Endomorphisms and automorphisms of the shift dynamical system. Math. Systems Theory 3 (1969), 320–375.10.1007/BF01691062CrossRefGoogle Scholar
Hochman, M.. On the automorphism groups of multidimensional shifts of finite type. Ergod. Th. & Dynam. Sys. 30(3) (2010), 809–840.CrossRefGoogle Scholar
Kim, K. H. and Roush, F. W.. On the automorphism groups of subshifts. Pure Math. Appl. Ser. B 1(4) (1990), 203–230.Google Scholar
Kitchens, B. P.. Symbolic Dynamics: One-sided, Two-sided and Countable State Markov Shifts. Springer, Berlin, 1998.10.1007/978-3-642-58822-8CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Lyndon, R. C.. On Burnside’s problem. Trans. Amer. Math. Soc. 77 (1954), 202–215.Google Scholar
Ryan, J. P.. The shift and commutativity. Math. Systems Theory 6 (1972), 82–85.CrossRefGoogle Scholar
Ryan, J. P.. The shift and commutativity II. Math. Systems Theory 8(3) (1974), 249–250.CrossRefGoogle Scholar
Weiss, B.. Subshifts of finite type and sofic systems. Monatsh. Math. 77 (1973), 462–474.10.1007/BF01295322CrossRefGoogle Scholar