Hostname: page-component-5c6d5d7d68-vt8vv Total loading time: 0.001 Render date: 2024-08-16T15:06:10.287Z Has data issue: false hasContentIssue false
  • English
  • Français

On the norm convergence of non-conventional ergodic averages

Published online by Cambridge University Press:  23 June 2009

TIM AUSTIN
TIM AUSTIN*
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA 90095-1555, USA (email: timaustin@math.ucla.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

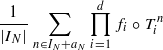We offer a proof of the following non-conventional ergodic theorem: If Ti:ℤr↷(X,Σ,μ) for i=1,2,…,d are commuting probability-preserving ℤr-actions, (IN)N≥1 is a Følner sequence of subsets of ℤr, (aN)N≥1 is a base-point sequence in ℤr and f1,f2,…,fd∈L∞(μ) then the non-conventional ergodic averages converge to some limit in L2(μ) that does not depend on the choice of (aN)N≥1 or (IN)N≥1. The leading case of this result, with r=1 and the standard sequence of averaging sets, was first proved by Tao, following earlier analyses of various more special cases and related results by Conze and Lesigne, Furstenberg and Weiss, Zhang, Host and Kra, Frantzikinakis and Kra and Ziegler. While Tao’s proof rests on a conversion to a finitary problem, we invoke only techniques from classical ergodic theory, so giving a new proof of his result.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 30 , Issue 2 , April 2010 , pp. 321 - 338
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bergelson, V.. Weakly mixing PET. Ergod. Th. & Dynam. Sys. 7(3) (1987), 337–349.CrossRefGoogle Scholar
[2]Bergelson, V. and Leibman, A.. A nilpotent Roth theorem. Invent. Math. 147(2) (2002), 429–470.CrossRefGoogle Scholar
[3]Bergelson, V., McCutcheon, R. and Zhang, Q.. A Roth theorem for amenable groups. Amer. J. Math. 119(6) (1997), 1173–1211.CrossRefGoogle Scholar
[4]Conze, J.-P. and Lesigne, E.. Théorèmes ergodiques pour des mesures diagonales. Bull. Soc. Math. France 112(2) (1984), 143–175.CrossRefGoogle Scholar
[5]Conze, J.-P. and Lesigne, E.. Sur un théorème ergodique pour des mesures diagonales. Probabilités (Publications de l’Institut de recherche mathématique de Rennes, 1987). Université de Rennes I, Rennes, 1988, pp. 1–31.Google Scholar
[6]Conze, J.-P. and Lesigne, E.. Sur un théorème ergodique pour des mesures diagonales. C. R. Acad. Sci. Paris Sér. I Math. 306(12) (1988), 491–493.Google Scholar
[7]Frantzikinakis, N. and Kra, B.. Convergence of multiple ergodic averages for some commuting transformations. Ergod. Th. & Dynam. Sys. 25(3) (2005), 799–809.CrossRefGoogle Scholar
[8]Furstenberg, H.. Ergodic behaviour of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.CrossRefGoogle Scholar
[9]Furstenberg, H. and Weiss, B.. A mean ergodic theorem for . Convergence in Ergodic Theory and Probability. Eds. Bergleson, V., March, A. and Rosenblatt, J.. De Gruyter, Berlin, 1996, pp. 193–227.CrossRefGoogle Scholar
[10]Glasner, E.. Ergodic Theory via Joinings. American Mathematical Society, Providence, RI, 2003.CrossRefGoogle Scholar
[11]Host, B.. Ergodic seminorms for commuting transformations and applications. Preprint. Available online at arXiv.org.0811.3703, 2008.Google Scholar
[12]Host, B. and Kra, B.. Convergence of Conze–Lesigne averages. Ergod. Th. & Dynam. Sys. 21(2) (2001), 493–509.CrossRefGoogle Scholar
[13]Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.CrossRefGoogle Scholar
[14]Leibman, A.. Pointwise convergence of ergodic averages for polynomial sequences of translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25(1) (2005), 201–213.CrossRefGoogle Scholar
[15]Nadkarni, M. G.. Spectral theory of dynamical systems. Birkhäuser Advanced Texts: Basler Lehrbücher. [Birkhäuser Advanced Texts: Basel Textbooks]. Birkhäuser, Basel, 1998.Google Scholar
[16]Tao, T.. Norm convergence of multiple ergodic averages for commuting transformations. Ergod. Th. & Dynam. Sys. 28 (2008), 657–688.CrossRefGoogle Scholar
[17]Towsner, H. P.. Convergence of diagonal ergodic averages. Preprint, available online at arXiv.org: 0711.1180, 2007.Google Scholar
[18]Zhang, Q.. On convergence of the averages (1/N)∑ Nn=1f1(Rnx)f2(Snx)f3(Tnx). Monatsh. Math. 122(3) (1996), 275–300.CrossRefGoogle Scholar
[19]Ziegler, T.. A non-conventional ergodic theorem for a nilsystem. Ergod. Th. & Dynam. Sys. 25(4) (2005), 1357–1370.CrossRefGoogle Scholar
[20]Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20(1) (2007), 53–97 (electronic).CrossRefGoogle Scholar