Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-08T13:28:35.700Z Has data issue: false hasContentIssue false
  • English
  • Français

The scenery flow of self-similar measures with weak separation condition

Part of: Ergodic theory Measure-theoretic ergodic theory Classical measure theory

Published online by Cambridge University Press:  06 August 2021

ALEKSI PYÖRÄLÄ Open the ORCID record for ALEKSI PYÖRÄLÄ [Opens in a new window]
ALEKSI PYÖRÄLÄ*
Affiliation:
Research Unit of Mathematical Sciences, University of Oulu, PO Box 8000, FI-90014, Oulu, Finland
*
e-mail: aleksi.pyorala@oulu.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that self-similar measures on 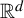$\mathbb R^d$ satisfying the weak separation condition are uniformly scaling. Our approach combines elementary ergodic theory with geometric analysis of the structure given by the weak separation condition.

Keywords

scenery flowself-similar measureweak separation conditionuniformly scaling measure

MSC classification

Primary: 37A10: One-parameter continuous families of measure-preserving transformations
Secondary: 28A80: Fractals 28D05: Measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 10 , October 2022 , pp. 3167 - 3190
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Algom, A., Rodriguez Hertz, F. and Wang, Z.. Pointwise normality and Fourier decay for self-conformal measures. Preprint, 2021, arXiv:2012.06529.CrossRefGoogle Scholar
Dayan, Y., Ganguly, A. and Weiss, B.. Random walks on tori and normal numbers in self-similar sets. Preprint, 2020, arXiv:2002.00455.Google Scholar
Erdös, P.. On a family of symmetric Bernoulli convolutions. Amer. J. Math. 61 (1939), 974–976.CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications. Wiley, Hoboken, NJ, 2013.Google Scholar
Feng, D.-J.. Gibbs properties of self-conformal measures and the multifractal formalism. Ergod. Th. & Dynam. Sys. 27(3) (2007), 787–812.CrossRefGoogle Scholar
Feng, D.-J.. Uniformly scaling property of self-similar measures with the finite type condition. Unpublished manuscript.Google Scholar
Feng, D.-J. and Lau, K.-S.. Multifractal formalism for self-similar measures with weak separation condition. J. Math. Pures Appl. (9) 92(4) (2009), 407–428.CrossRefGoogle Scholar
Ferguson, A., Fraser, J. M. and Sahlsten, T.. Scaling scenery of $\left(\times m,\times n\right)$ invariant measures. Adv. Math. 268 (2015), 564–602.CrossRefGoogle Scholar
Fraser, J. M., Henderson, A. M., Olson, E. J. and Robinson, J. C.. On the Assouad dimension of self-similar sets with overlaps. Adv. Math. 273 (2015), 188–214.CrossRefGoogle Scholar
Fraser, J. and Pollicott, M.. Uniform scaling limits for ergodic measures. J. Fractal Geom. 4(1) (2017), 1–19.CrossRefGoogle Scholar
Furstenberg, H.. Ergodic fractal measures and dimension conservation. Ergod. Th. & Dynam. Sys. 28(2) (2008), 405–422.CrossRefGoogle Scholar
Garsia, A. M.. Arithmetic properties of Bernoulli convolutions. Trans. Amer. Math. Soc. 102 (1962), 409–432.CrossRefGoogle Scholar
Gavish, M.. Measures with uniform scaling scenery. Ergod. Th. & Dynam. Sys. 31(1) (2011), 33–48.CrossRefGoogle Scholar
Hare, K., Hare, K. and Rutar, A.. When the weak separation condition implies the generalized finite type condition. Proc. Amer. Math. Soc. 149(4) (2020), 1555–1568.CrossRefGoogle Scholar
Hochman, M.. Dynamics on fractals and fractal distributions. Preprint, 2013, arXiv:1008.3731.Google Scholar
Hochman, M.. On self-similar sets with overlaps and inverse theorems for entropy. Ann. of Math. (2) 180(2) (2014), 773–822.CrossRefGoogle Scholar
Hochman, M.. Dimension theory of self-similar sets and measures. Proc. Int. Congress of Mathematicians—Rio de Janeiro 2018. Vol. III. Invited Lectures. Eds. Sirakov, B., Ney de Souza, P. and Viana, M.. World Scientific Publishing, Hackensack, NJ, 2018, pp. 1949–1972.Google Scholar
Hochman, M. and Shmerkin, P.. Local entropy averages and projections of fractal measures. Ann. of Math. (2) 175(3) (2012), 1001–1059.CrossRefGoogle Scholar
Hochman, M. and Shmerkin, P.. Equidistribution from fractal measures. Invent. Math. 202(1) (2015), 427–479.CrossRefGoogle Scholar
Kac, M.. On the notion of recurrence in discrete stochastic processes. Bull. Amer. Math. Soc. 53 (1947), 1002–1010.CrossRefGoogle Scholar
Käenmäki, A. and Rossi, E.. Weak separation condition, Assouad dimension, and Furstenberg homogeneity. Ann. Acad. Sci. Fenn. Math. 41(1) (2016), 465–490.CrossRefGoogle Scholar
Kakutani, S.. Random ergodic theorems and Markoff processes with a stable distribution. Proc. 2nd Berkeley Symp. on Mathematical Statistics and Probability. Ed. Neyman, J.. University of California Press, Berkeley, 1951, pp. 247–261.Google Scholar
Kim, H. J.. Skew product action. Int. J. Contemp. Math. Sci. 1(5–8) (2006), 205–211.CrossRefGoogle Scholar
Lau, K.-S. and Ngai, S.-M.. Multifractal measures and a weak separation condition. Adv. Math. 141(1) (1999), 45–96.CrossRefGoogle Scholar
Lau, K.-S. and Ngai, S.-M.. A generalized finite type condition for iterated function systems. Adv. Math. 208(2) (2007), 647–671.CrossRefGoogle Scholar
Lau, K.-S. and Wang, X.-Y.. Iterated function systems with a weak separation condition. Studia Math. 161(3) (2004), 249–268.CrossRefGoogle Scholar
O’Neil, T.. A measure with a large set of tangent measures. Proc. Amer. Math. Soc. 123(7) (1995), 2217–2220.CrossRefGoogle Scholar
Shmerkin, P.. On Furstenberg’s intersection conjecture, self-similar measures, and the ${L}^q$ norms of convolutions. Ann. of Math. (2) 189(2) (2019), 319–391.CrossRefGoogle Scholar
Varjú, P. P.. On the dimension of Bernoulli convolutions for all transcendental parameters. Ann. of Math. (2) 189(3) (2019), 1001–1011.CrossRefGoogle Scholar
Zerner, M. P. W.. Weak separation properties for self-similar sets. Proc. Amer. Math. Soc. 124(11) (1996), 3529–3539.CrossRefGoogle Scholar