No CrossRef data available.
Article contents
Schmidt games and Cantor winning sets
Published online by Cambridge University Press: 19 April 2024
Abstract
Schmidt games and the Cantor winning property give alternative notions of largeness, similar to the more standard notions of measure and category. Being intuitive, flexible, and applicable to recent research made them an active object of study. We survey the definitions of the most common variants and connections between them. A new game called the Cantor game is invented and helps with presenting a unifying framework. We prove surprising new results such as the coincidence of absolute winning and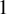 
$1$ Cantor winning in metric spaces, and the fact that 
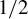$1/2$ winning implies absolute winning for subsets of 
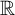$\mathbb {R}$. We also suggest a prototypical example of a Cantor winning set to show the ubiquity of such sets in metric number theory and ergodic theory.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
An, J.. Badziahin–Pollington–Velani’s theorem and Schmidt’s game. Bull. Lond. Math. Soc. 45(4) (2013), 721–733.CrossRefGoogle Scholar
An, J.. 2-dimensional badly approximable vectors and Schmidt’s game. Duke Math. J. 165(2) (2016), 267–284.Google Scholar
An, J., Ghosh, A., Guan, L. and Ly, T.. Bounded orbits of diagonalizable flows on finite volume quotients of products of sl2(r). Adv. Math. 354 (2019), 106743.CrossRefGoogle Scholar
An, J., Guan, L. and Kleinbock, D.. Bounded orbits of diagonalizable flows on
${\mathrm{SL}}_3(\mathbb{R})/{\mathrm{SL}}_3(\mathbb{Z})$
. Int. Math. Res. Not. IMRN 2015(24) (2015), 13623–13652.CrossRefGoogle Scholar
${\mathrm{SL}}_3(\mathbb{R})/{\mathrm{SL}}_3(\mathbb{Z})$
. Int. Math. Res. Not. IMRN 2015(24) (2015), 13623–13652.CrossRefGoogle ScholarBadziahin, D. and Harrap, S.. Cantor-winning sets and their applications. Adv. Math. 318 (2017), 627–677.CrossRefGoogle Scholar
Badziahin, D., Pollington, A. and Velani, S.. On a problem in simultaneous Diophantine approximation: Schmidt’s conjecture. Ann. of Math. (2) 174(3) (2011), 1837–1883.CrossRefGoogle Scholar
Badziahin, D. and Velani, S.. Multiplicatively badly approximable numbers and generalised Cantor sets. Adv. Math. 228(5) (2011), 2766–2796.Google Scholar
Beresnevich, V.. Badly approximable points on manifolds. Invent. Math. 202(3) (2015), 1199–1240.CrossRefGoogle Scholar
Bilyk, D., Ma, X., Pipher, J. and Spencer, C.. Diophantine approximations and directional discrepancy of rotated lattices. Trans. Amer. Math. Soc. 368(6) (2016), 3871–3897.Google Scholar
Broderick, R., Bugeaud, Y., Fishman, L., Kleinbock, D. and Weiss, B.. Schmidt’s game, fractals, and numbers normal to no base. Math. Res. Lett. 17 (2010), 307–321.CrossRefGoogle Scholar
Broderick, R., Fishman, L., Kleinbock, D., Reich, A. and Weiss, B.. The set of badly approximable vectors is strongly
${\mathrm{C}}^1$
incompressible. Math. Proc. Cambridge Philos. Soc. 153(2) (2012), 319–339.CrossRefGoogle Scholar
${\mathrm{C}}^1$
incompressible. Math. Proc. Cambridge Philos. Soc. 153(2) (2012), 319–339.CrossRefGoogle ScholarCampos, S. and Gelfert, K.. Exceptional sets for nonuniformly expanding maps. Nonlinearity 29(4) (2016), 1238–1256.Google Scholar
Campos, S. and Gelfert, K.. Exceptional sets for nonuniformly hyperbolic diffeomorphisms. J. Dynam. Differential Equations 31(2) (2019), 979–1004.CrossRefGoogle Scholar
Chaika, J., Cheung, Y. and Masur, H.. Winning games for bounded geodesics in moduli spaces of quadratic differentials. J. Mod. Dyn. 7(3) (2013), 395–427.CrossRefGoogle Scholar
Dani, S. G.. On badly approximable numbers, Schmidt games and bounded orbits of flows. Number Theory and Dynamical Systems (York, 1987) (London Mathematical Society Lecture Note series, 134). Ed. Dodson, M. M. and Vickers, J. A. G.. Cambridge University Press, Cambridge, 1989, pp. 69–86.CrossRefGoogle Scholar
Davenport, H.. A note on Diophantine approximation. II. Mathematika 11 (1964), 50–58.CrossRefGoogle Scholar
Einsiedler, M. and Tseng, J.. Badly approximable systems of affine forms, fractals, and Schmidt games. J. Reine Angew. Math. 660 (2011), 83–97.Google Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd., Chichester, 1990.Google Scholar
Färm, D.. Simultaneously non-dense orbits under different expanding maps. Dyn. Syst. 25(4) (2010), 531–545.CrossRefGoogle Scholar
Färm, D. and Persson, T.. Non-typical points for
$\unicode{x3b2}$
-shifts. Bull. Pol. Acad. Sci. Math. 61(2) (2013), 123–132.Google Scholar
$\unicode{x3b2}$
-shifts. Bull. Pol. Acad. Sci. Math. 61(2) (2013), 123–132.Google ScholarFärm, D., Persson, T. and Schmeling, J.. Dimension of countable intersections of some sets arising in expansions in non-integer bases. Fund. Math. 209 (2010), 157–176.CrossRefGoogle Scholar
Fishman, L.. Schmidt’s game, badly approximable matrices and fractals. J. Number Theory 129(9) (2009), 2133–2153.CrossRefGoogle Scholar
Fishman, L., Ly, T. and Simmons, D.. Determinacy and indeterminacy of games played on complete metric spaces. Bull. Aust. Math. Soc. 90 (2014), 339–351.CrossRefGoogle Scholar
Fishman, L., Simmons, D. and Urbański, M.. Diophantine approximation and the geometry of limit sets in Gromov hyperbolic metric spaces. Mem. Amer. Math. Soc. 254(1215) (2018), v+137.Google Scholar
Furstenberg, H.. Ergodic Theory and Fractal Geometry (CBMS Regional Conference Series in Mathematics, 120). American Mathematical Society, Providence, RI, 2014.CrossRefGoogle Scholar
Guan, L. and Yu, J.. Weighted badly approximable vectors and games. Int. Math. Res. Not. IMRN 2019(3) (2019), 810–833.Google Scholar
Haynes, A., Koivusalo, H., Walton, J. and Sadun, L.. Gaps problems and frequencies of patches in cut and project sets. Math. Proc. Cambridge Philos. Soc. 161(1) (2016), 65–85.CrossRefGoogle Scholar
Hutchinson, J.. Fractals and self-similarity. Indiana Univ. Math. J. 30(5) (1981), 713–747.CrossRefGoogle Scholar
Kleinbock, D. and Weiss, B.. Modified Schmidt games and Diophantine approximation with weights. Adv. Math. 223 (2010), 1276–1298.CrossRefGoogle Scholar
Mayeda, D. and Merrill, K.. Limit points badly approximable by horoballs. Geom. Dedicata 163 (2013), 127–140.Google Scholar
McMullen, C.. Winning sets, quasiconformal maps and Diophantine approximation. Geom. Funct. Anal. 20(3) (2010), 726–740.CrossRefGoogle Scholar
Moshchevitin, N.. A note on badly approximable affine forms and winning sets. Mosc. Math. J. 11(1) (2011), 129–137.CrossRefGoogle Scholar
Nesharim, E. and Simmons, D..
$\mathbf{Bad}({s},{t})$
is hyperplane absolute winning. Acta Arith. 164(2) (2014), 145–152.Google Scholar
$\mathbf{Bad}({s},{t})$
is hyperplane absolute winning. Acta Arith. 164(2) (2014), 145–152.Google ScholarPollington, A. and Velani, S.. Metric Diophantine approximation and “absolutely friendly” measures. Selecta Math. (N.S.) 11 (2005), 297–307.Google Scholar
Schmidt, W. M.. On badly approximable numbers and certain games. Trans. Amer. Math. Soc. 123 (1966), 27–50.CrossRefGoogle Scholar
Schmidt, W. M.. Diophantine Approximation (Lecture Notes in Mathematics, 785). Springer-Verlag, Berlin, 1980.Google Scholar
Tseng, J.. Badly approximable affine forms and Schmidt games. J. Number Theory 129 (2009), 3020–3025.Google Scholar
Wu, W.. On non-dense orbits of certain non-algebraic dynamical systems. J. Dynam. Differential Equations 30 (2016), 501–519.CrossRefGoogle Scholar
Wu, W.. Schmidt games and non-dense forward orbits of certain partially hyperbolic systems. Ergod. Th. & Dynam. Sys. 36(5) (2016), 1656–1678.CrossRefGoogle Scholar
Yang, L.. Badly approximable points on manifolds and unipotent orbits in homogeneous spaces. Geom. Funct. Anal. 29(4) (2019), 1194–1234.CrossRefGoogle Scholar