Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T21:40:23.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Smale flows on 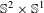$\mathbb{S}^{2}\times \mathbb{S}^{1}$

Published online by Cambridge University Press:  13 April 2015

KETTY A. DE REZENDE ,
GUIDO G. E. LEDESMA  and
OZIRIDE MANZOLI NETO
KETTY A. DE REZENDE
Affiliation:
Department of Mathematics, Institute of Mathematics, Statistics and Scientific Computation, Unicamp, Campinas, São Paulo, Brazil email ketty@ime.unicamp.br
GUIDO G. E. LEDESMA
Affiliation:
Department of Mathematics, Institute of Mathematics, Statistics and Scientific Computation, Unicamp, Campinas, São Paulo, Brazil email ketty@ime.unicamp.br
OZIRIDE MANZOLI NETO
Affiliation:
Institute of Mathematical Sciences and Computation, University of São Paulo, São Carlos, São Paulo, Brazil
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we use abstract Lyapunov graphs as a combinatorial tool to obtain a complete classification of Smale flows on 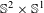$\mathbb{S}^{2}\times \mathbb{S}^{1}$. This classification gives necessary and sufficient conditions that must be satisfied by an (abstract) Lyapunov graph in order for it to be associated to a Smale flow on 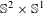$\mathbb{S}^{2}\times \mathbb{S}^{1}$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1546 - 1581
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Béguin, F. and Bonatti, Ch.. Flots de Smale en dimension 3: présentations finies de voisinages invariants d’ensembles selles. Topology 41(1) (2002), 119–162.CrossRefGoogle Scholar
Bonatti, Ch. and Grines, V.. Knots as topological invariants for gradient-like diffeomorphisms of the sphere S 3. J. Dyn. Control Syst. 6(4) (2000), 579–602.CrossRefGoogle Scholar
Bowen, R.. One-dimensional hyperbolic sets for flows. J. Differential Equations 12(1) (1972), 173–179.CrossRefGoogle Scholar
Bowen, R. and Franks, J.. Homology for zero-dimensional nonwandering sets. Ann. of Math. (2) 106(1) (1977), 73–92.CrossRefGoogle Scholar
Conley, C. C.. Isolated Invariant Sets and the Morse Index. American Mathematical Society, Providence, RI, 1978.CrossRefGoogle Scholar
Cruz, R. and de Rezende, K.. Cycle rank of Lyapunov graphs and the genera of manifolds. Proc. Amer. Math. Soc. 126(12) (1998), 3715–3720.CrossRefGoogle Scholar
de Rezende, K.. Smale flows on the three-sphere. Trans. Amer. Math. Soc. 303(1) (1987), 283–310.CrossRefGoogle Scholar
de Rezende, K.. Gradient-like flows on 3-manifolds. Ergod. Th. & Dynam. Sys. 13(3) (1993), 557–580.CrossRefGoogle Scholar
Franks, J.. Homology and Dynamical Systems. American Mathematical Society, Providence, RI, 1982.CrossRefGoogle Scholar
Franks, J.. Nonsingular Smale flows on S 3. Topology 24(3) (1985), 265–282.CrossRefGoogle Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. (N.S.) 73(6) (1967), 747–817.CrossRefGoogle Scholar
Wilson, W.. Smoothing derivatives of functions and applications. Trans. Amer. Math. Soc. 139 (1969), 413–428.CrossRefGoogle Scholar
Yu, B.. Lyapunov graphs of nonsingular Smale flows on S 1 × S 2. Trans. Amer. Math. Soc. 365(2) (2012), 767–783.CrossRefGoogle Scholar