The unstable-unstable pair bifurcation is a bifurcation in which two unstable fixed points or periodic orbits of the same period coalesce and disappear as a system paremeter is raised. For parameter values just above that at which unstable orbits are destroyed there can be chaotic transients. Then, as the bifurcation is approached from above, the average length of a chaotic transient diverges, and, below the bifurcation point, the chaotic transient may be regarded as having been converted into a chaotic attractor. It is argued that unstable-unstable pair bifurcations should be expected to occur commonly in dynamical systems. This bifurcation is an example of the crisis route to chaos. The most striking fact about unstable-unstable pair bifurcation crises is that long chaotic transients persist even for parameter values relatively far from the bifurcation point. These long-lived chaotic transients may prevent the time asymptotic state from being reached during experiments. An expression giving a lower bound for the average lifetime of a chaotic transient is derived and shown to agree well with numerical experiments. In particular, this bound on the average lifetime, (τ), satisfies

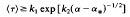
for α near α*, where k1 and k2 are constants and α* is the value of the parameter a at which the crisis occurs. Thus, as a approaches α* from above, (τ) increases more rapidly than any power of (α − α*)−1. Finally, we discuss the effect of adding bounded noise (small random perturbations) on these phenomena and argue that the chaotic transients should be lengthened by noise.