This article is devoted to the optimal control of state equations with memory of the form:

$\dot{x}(t)=F(x(t),u(t), \int_0^{+\infty} A(s) x(t-s) {\rm d}s), \; t>0,$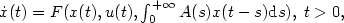

with initial conditions $x(0)=x, \; x(-s)=z(s), s>0$.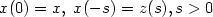

Denoting by $y_{x, z, u}$ the solution of the previous Cauchy problem and:

$ v(x,z):=\inf_{u\in V} \lbrace \int_0^{+\infty} {\rm e}^{-\lambda s } L(y_{x,z,u}(s), u(s)){\rm d}s\rbrace $

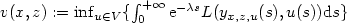
where V is a class of admissible controls, we prove that v is the only viscosity solution of an Hamilton-Jacobi-Bellman equation of the form:

$ \lambda v(x,z)+H(x,z,\nabla_x v(x,z))+\langle D_z v(x,z), \dot{z} \rangle=0 $

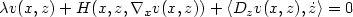
in the sense of the theory of viscosity solutions in infinite-dimensions of Crandall and Lions.