Hostname: page-component-5c6d5d7d68-xq9c7 Total loading time: 0 Render date: 2024-09-01T09:24:02.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Newton and conjugate gradient for harmonic maps from the disc into the sphere

Published online by Cambridge University Press:  15 February 2004

Morgan Pierre
Morgan Pierre*
Affiliation:
Centre de Mathématiques et de Leurs Applications, École Normale Supérieure de Cachan, 61 avenue du Président Wilson, 94235 Cachan Cedex, France; Morgan.Pierre@cmla.ens-cachan.fr.
Get access

Abstract

We compute numerically the minimizers of the Dirichlet energy $$E(u)=\frac{1}{2}\int_{B^2}|\nabla u|^2 {\rm d}x$$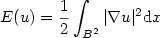 among maps $u:B^2\to S^2$ 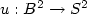from the unit disc into the unit sphere that satisfy a boundary condition and a degree condition. We use a Sobolev gradient algorithm for the minimization and we prove that its continuous version preserves the degree. For the discretization of the problem we use continuous P1 finite elements. We propose an original mesh-refining strategy needed to preserve the degree with the discrete version of the algorithm (which is a preconditioned projected gradient). In order to improve the convergence, we generalize to manifolds the classical Newton and conjugate gradient algorithms. We give a proof of the quadratic convergence of the Newton algorithm for manifolds in a general setting.

Keywords

Harmonic mapsfinite elementsmesh-refinementSobolev gradientNewton algorithmconjugate gradient.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 10 , Issue 1 , January 2004 , pp. 142 - 167
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

F. Alouges, A new algorithm for computing liquid crystal stable configurations: the harmonic mapping case. SIAM J. Numer. Anal. 34 (1997) 1708–1726.
F. Alouges and B.D. Coleman, Numerical bifurcation of equilibria of nematic crystals between non-co-axial cylinders. Math. Models Methods Appl. Sci. 11 (2001) 459–473.
D. Braess, Finite elements, in Theory, fast solvers, and applications in solid mechanics. Translated from the 1992 German edition by Larry L. Schumaker. Cambridge University Press, Cambridge, 2nd edn. (2001).
H. Brézis, Analyse fonctionnelle. Masson (1996).
H. Brézis and J.-M. Coron, Large solutions for harmonic maps in two dimensions. Comm. Math. Phys. 92 (1983) 203–215.
K.-C. Chang, W.-Y. Ding and R. Ye, Finite-time blow up of the heat flow of harmonic maps from surfaces. J. Differ. Geom. 36 (1992) 507–515.
P.G. Ciarlet, Introduction à l'analyse numérique matricielle et à l'optimisation. Masson (1988).
P.-G. De Gennes and J. Prost, The physics of liquid crystals. Clarendon Press, Oxford (1993).
R. Fletcher and C.M. Reeves, Function minimization by conjugate gradients. Comput. J. 7 (1994) 149–154.
M. Giaquinta, G. Modica and J. Souček, Cartesian currents in the calculus of variations. I. Springer-Verlag, Berlin (1998).
M. Giaquinta, G. Modica and J. Souček, Cartesian currents in the calculus of variations. II. Springer-Verlag, Berlin (1998).
R.M. Hardt, Singularities of harmonic maps. Bull. Amer. Math. Soc. (N.S.) 34 (1997) 15–34.
E. Hebey, Introduction à l'analyse non linéaire sur les variétés. Diderot Editeur Arts et Sciences (1987).
F. Hélein, Régularité des applications faiblement harmoniques entre une surface et une sphère. C. R. Acad. Sci. Paris Sér. I Math. 311 (1990) 519–524.
F. Hélein, Symétries dans les problèmes variationnels et applications harmoniques. Istituti Editoriali e Poligrafici Internazionali, Pisa-Roma (1998).
J. Jost, Harmonic mappings betwenn surfaces. Springer-verlag, Lecture Notes in Math. 1062 (1984).
W.P.A Klingenberg, Riemannian Geometry. Walter de Gruyter (1995).
E. Kuwert, Minimizing the energy of maps from a surface into a 2-sphere with prescribed degree and boundary values. Manuscripta Math. 83 (1994) 31–38.
L. Lemaire, Applications harmoniques de surfaces riemanniennes. J. Differ. Geom. 13 (1978) 51–78.
A. Lichnewsky, Une méthode de gradient conjugué sur des variétés : application à certains problèmes de valeurs propres non linéaires. Numer. Funct. Anal. Optim. 1 (1979) 515–560.
P.L. Lions, The concentration-compactness principle in the calculus of variations. The limit case, part 2. Rev. Mat. Iberoamericana 1 (1985) 45–121.
C.B. Morrey, Multiple integrals in the calculus of variations. Springer, New York (1966).
J.W. Neuberger, Sobolev gradients and boundary conditions for partial differential equations, in Recent developments in optimization theory and nonlinear analysis (Jerusalem, 1995), Amer. Math. Soc., Providence, RI. Contemp. Math. 204 (1997) 171–181
E. Polak, Optimization, Appl. Math. Sci. 124 (1997).
J. Qing, Remark on the Dirichlet problem for harmonic maps from the disc into the 2-sphere. Proc. R. Soc. Edinb. 122A (1992) 63–67.
J. Qing, Boundary regularity of weakly harmonic maps from surfaces. J. Funct. Anal. 114 (1993) 63–67.
R. Schoen and K. Uhlenbeck, Boundary regularity and the Dirichlet problem for harmonic maps. J. Dif. Geom. 18 (1983) 253–268.
J.R. Shewchuk, Triangle: engineering a 2d quality mesh generator and delaunay triangulator. http://www-2.cs.cmu.edu/quake/triangle.html.
J.R. Shewchuk, An introduction to the conjugate gradient method without the agonizing pain. http://www-2.cs.cmu.edu/jrs/jrspapers.html#cg (1994).
A. Soyeur, The Dirichlet problem for harmonic maps from the disc into the 2-sphere. Proc. R. Soc. Edinb. 113A (1989) 229–234.