Article contents
On indecomposable sets with applications
Published online by Cambridge University Press: 28 March 2014
Abstract
In this note we show the characteristic function of every indecomposable set
F in the
plane is BV
equivalent to the characteristic function a closed set See Formula in PDF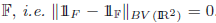 \hbox{See Formula in PDF}.
We show by example this is false in dimension three and above. As a corollary to this
result we show that for every ϵ > 0 a set of finite perimeter S can be approximated by a
closed subset See Formula in PDF
\hbox{See Formula in PDF}.
We show by example this is false in dimension three and above. As a corollary to this
result we show that for every ϵ > 0 a set of finite perimeter S can be approximated by a
closed subset See Formula in PDF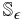 \hbox{See Formula in PDF} with finitely many indecomposable
components and with the property that See Formula in PDF
\hbox{See Formula in PDF} with finitely many indecomposable
components and with the property that See Formula in PDF \hbox{See Formula in PDF}
and See Formula in PDF
\hbox{See Formula in PDF}
and See Formula in PDF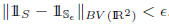 \hbox{See Formula in PDF}.
We apply this corollary to give a short proof that locally quasiminimizing sets in the
plane are BVl
extension domains.
\hbox{See Formula in PDF}.
We apply this corollary to give a short proof that locally quasiminimizing sets in the
plane are BVl
extension domains.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 20 , Issue 2 , April 2014 , pp. 612 - 631
- Copyright
- © EDP Sciences, SMAI, 2014
References
- 1
- Cited by




