Article contents
The geometrical quantity in damped wave equations on a square
Published online by Cambridge University Press: 11 October 2006
Abstract
The energy in a square membrane Ω subject to constant viscous damping
on a subset $\omega\subset \Omega$ decays exponentially in time
as soon as ω
satisfies a geometrical condition known as the “Bardos-Lebeau-Rauch” condition. The rate
$\tau(\omega)$
decays exponentially in time
as soon as ω
satisfies a geometrical condition known as the “Bardos-Lebeau-Rauch” condition. The rate
$\tau(\omega)$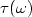 of this decay satisfies $\tau(\omega)= 2 \min( -\mu(\omega), g(\omega))$
of this decay satisfies $\tau(\omega)= 2 \min( -\mu(\omega), g(\omega))$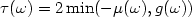 (see Lebeau [Math.
Phys. Stud.19 (1996) 73–109]). Here $\mu(\omega)$
(see Lebeau [Math.
Phys. Stud.19 (1996) 73–109]). Here $\mu(\omega)$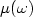 denotes the spectral abscissa of the
damped wave equation operator and $g(\omega)$
denotes the spectral abscissa of the
damped wave equation operator and $g(\omega)$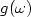 is a number called
the geometrical quantity of ω and defined as follows.
A ray in Ω is the trajectory generated by the
free motion of a mass-point in Ω subject to elastic reflections on the
boundary. These reflections obey the law of geometrical optics.
The geometrical quantity $g(\omega)$
is a number called
the geometrical quantity of ω and defined as follows.
A ray in Ω is the trajectory generated by the
free motion of a mass-point in Ω subject to elastic reflections on the
boundary. These reflections obey the law of geometrical optics.
The geometrical quantity $g(\omega)$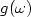 is then defined as the upper limit (large time
asymptotics) of the average trajectory length.
We give here an algorithm to compute explicitly
$g(\omega)$
is then defined as the upper limit (large time
asymptotics) of the average trajectory length.
We give here an algorithm to compute explicitly
$g(\omega)$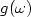 when ω
is a finite union of squares.
when ω
is a finite union of squares.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 12 , Issue 4 , October 2006 , pp. 636 - 661
- Copyright
- © EDP Sciences, SMAI, 2006
References
- 2
- Cited by




