Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-08T23:55:18.261Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower semicontinuity of multiple µ-quasiconvex integrals

Published online by Cambridge University Press:  15 September 2003

Ilaria Fragalà
Ilaria Fragalà*
Affiliation:
Dipartimento di Matematica, Politecnico di Milano, Piazza Leonardo da Vinci 32, 20133 Milano, Italy; fragala@mate.polimi.it.
Get access

Abstract

Lower semicontinuity results are obtained for multiple integrals of the kind $\int _{\mathbb{R}^n}\!f(x, \!\nabla_\mu u\!){\rm d} \mu$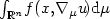, where μ is a given positive measure on $\mathbb{R}^n$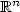, and the vector-valued function u belongs to the Sobolev space $H ^{1,p}_\mu (\mathbb{R}^n, \mathbb{R}^m)$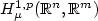 associated with μ. The proofs are essentially based on blow-up techniques, and a significant role is played therein by the concepts of tangent space and of tangent measures to μ. More precisely, for fully general μ, a notion of quasiconvexity for f along the tangent bundle to μ, turns out to be necessary for lower semicontinuity; the sufficiency of such condition is also shown, when μ belongs to a suitable class of rectifiable measures.

Keywords

Borel measurestangent propertieslower semicontinuity.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 9 , January 2003 , pp. 105 - 124
Copyright
© EDP Sciences, SMAI, 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E. and Fusco, N., Semicontinuity problems in the Calculus of Variations. Arch. Rational Mech. Anal. 86 (1984) 125-145. CrossRef
L. Ambrosio, Introduzione alla Teoria Geometrica della Misura e Applicazioni alle Superfici Minime, Lectures Notes. Scuola Normale Superiore, Pisa (1996).
Ambrosio, L., On the lower-semicontinuity of quasi-convex integrals in SBV. Nonlinear Anal. 23 (1994) 405-425. CrossRef
Ambrosio, L., Buttazzo, G. and Fonseca, I., Lower-semicontinuity problems in Sobolev spaces with respect to a measure. J. Math. Pures Appl. 75 (1996) 211-224.
Ball, J.M. and Murat, F., W 1,p -quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58 (1984) 225-253. CrossRef
Bouchitté, G. and Buttazzo, G., Characterization of optimal shapes and masses through Monge-Kantorovich equation. J. Eur. Math. Soc. 3 (2001) 139-168.
G. Bouchitté, G. Buttazzo and I. Fragalà, Mean curvature of a measure and related variational problems. Ann. Scuola Norm. Sup. Pisa. Cl. Sci. IV XXV (1997) 179-196.
Bouchitté, G., Buttazzo, G. and Fragalà, I., Convergence of Sobolev spaces on varying manifolds. J. Geom. Anal. 11 (2001) 399-422. CrossRef
Bouchitté, G., Buttazzo, G. and Seppecher, P., Energies with respect to a measure and applications to low dimensional structures. Calc. Var. Partial Differential Equations 5 (1997) 37-54. CrossRef
Bouchitté, G. and Fragalà, I., Homogenization of thin structures by two-scale method with respect to measures. SIAM J. Math. Anal. 32 (2001) 1198-1126. CrossRef
G. Bouchitté and I. Fragalà, Homogenization of elastic thin structures: A measure-fattening approach. J. Convex. Anal. (to appear).
A. Braides, Semicontinuity, Γ-convergence and Homogenization for Multiple Integrals, Lectures Notes. SISSA, Trieste (1994).
G. Buttazzo, Semicontinuity, Relaxation, and Integral Representation in the Calculus of Variations. Longman, Harlow, Pitman Res. Notes Math. Ser. 207 (1989).
B. Dacorogna, Direct Methods in the Calculus of Variations. Springer-Verlag, Berlin, Appl. Math. Sci. 78 (1988).
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions. CRC Press, Ann Harbor, Stud. in Adv. Math. (1992).
H. Federer, Geometric Measure Theory. Springer-Verlag, Berlin (1969).
Fonseca, I. and Müller, S., Quasi-convex integrands and lower semicontinuity in L 1. SIAM J. Math. Anal. 23 (1992) 1081-1098. CrossRef
Fragalà, I. and Mantegazza, C., On some notions of tangent space to a measure. Proc. Roy. Soc. Edinburgh 129A (1999) 331-342. CrossRef
P. Hajlasz and P. Koskela, Sobolev met Poincaré. Mem. Amer. Math. Soc. 145 (2000).
Hajlasz, P. and Koskela, P., Sobolev meets Poincaré. C. R. Acad. Sci. Paris 320 (1995) 1211-1215.
Ioffe, A.D., On lower semicontinuity of integral functionals I and II. SIAM J. Contol Optim. 15 (1997) 521-538 and 991-1000. CrossRef
Kristensen, J., Lower semicontinuity in spaces of weakly differentiable functions. J. Math. Ann. 313 (1999) 653-710. CrossRef
Maly, J., Lower semicontinuity of quasiconvex integrals. Manuscripta Math. 85 (1994) 419-428. CrossRef
J.P. Mandallena, Contributions à une approche générale de la régularisation variationnelle de fonctionnelles intégrales, Thèse de Doctorat. Université de Montpellier II (1999).
Marcellini, P., Approximation of quasiconvex functions, and lower semicontinuity of multiple integrals. Manuscripta Math. 51 (1985) 1-28. CrossRef
Marcellini, P. and Sbordone, C., On the existence of minima of multiple integrals in the Calculus of Variations. J. Math. Pures Appl. 62 (1983) 1-9.
P. Mattila, Geometry of Sets and Measures in Euclidean Spaces. Cambridge University Press, London (1995).
C.B. Morrey, Multiple Integrals in the Calculus of Variations. Springer-Verlag, Berlin (1966).
Olech, C., Weak lower semicontuity of integral functionals. J. Optim. Theory Appl. 19 (1976) 3-16. CrossRef
O'Neil, T., A measure with a large set of tangent measures. Proc. Amer. Math. Soc. 123 (1995) 2217-2221. CrossRef
Preiss, D., Geometry of measures on $\mathbb{R} ^n$ : Distribution, rectifiability and densities. Ann. Math. 125 (1987) 573-643. CrossRef
L. Simon, Lectures on Geometric Measure Theory. Australian Nat. Univ., Proc. Centre for Math. Anal. 3 (1983).
Valadier, M., Multiapplications mesurables à valeurs convexes compactes. J. Math. Pures Appl. 50 (1971) 265-297.
Zhikov, V.V., On an extension and an application of the two-scale convergence method. Mat. Sb. 191 (2000) 31-72. CrossRef