This work represents a first step towards the simulation of the motion of water in a complex hydrodynamic configuration, such as a channel network or a river delta, by means of a suitable “combination” of different mathematical models. In this framework a wide spectrum of space and time scales is involved due to the presence of physical phenomena of different nature. Ideally, moving from a hierarchy of hydrodynamic models, one should solve throughout the whole domain the most complex model (with solution $u_{\rm{fine}}$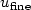) to accurately describe all the physical features of the problem at hand. In our approach instead, for a user-defined output functional ${\cal F}$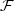, we aim to approximate, within a prescribed tolerance τ, the value ${\cal F}(u_{\rm{fine}})$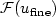 by means of the quantity ${\cal F}(u_{\rm{adapted}})$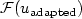, $u_{\rm{adap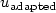ted}}$ being the so-called adapted solution solving the simpler models on most of the computational domain while confining the complex ones only on a restricted region. Moving from the simplified setting where only two hydrodynamic models, fine and coarse, are considered, we provide an efficient tool able to automatically select the regions of the domain where the coarse model rather than the fine one are to be solved, while guaranteeing $|{\cal F}(u_{\rm{fine}}) -{\cal F}(u_{\rm{adapted}})|$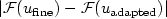 below the tolerance τ. This goal is achieved via a suitable a posteriori modeling error analysis developed in the framework of a goal-oriented theory. We extend the dual-based approach provided in [Braack and Ern, Multiscale Model Sim.1 (2003) 221–238], for steady equations to the case of a generic time-dependent problem. Then this analysis is specialized to the case we are interested in, i.e. the free-surface flows simulation, by emphasizing the crucial issue of the time discretization for both the primal and the dual problems. Finally, in the last part of the paper a widespread numerical validation is carried out.