We consider the following reaction-diffusion equation:

$$ {\rm (KS)} \left\{ \begin{array}{llll} u_t = \nabla \cdot \Big( \nabla u^m - u^{q-1} \nabla v \Big), & x \in \mathbb{R}^N, \ 0<t<\infty, \nonumber 0 = \Delta v - v + u, & x \in \mathbb{R}^N, \ 0<t<\infty, \nonumber u(x,0) = u_0(x), & x \in \mathbb{R}^N, \end{array} \right. $$

where $N \ge 1, \ m > 1, \ q \ge \max\{m+\frac{2}{N},2\}$.
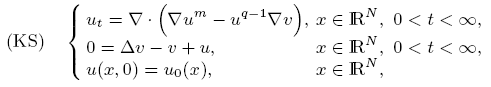
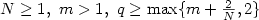In [Sugiyama, Nonlinear Anal.63 (2005) 1051–1062; Submitted; J. Differential Equations (in press)] it was shown that in the case of $q \ge \max\{m+\frac{2}{N},2\}$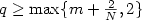, the above problem (KS) is solvable globally in time for “small $L^{\frac{N(q-m)}{2}}$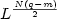 data”. Moreover, the decay of the solution (u,v) in $L^p(\mathbb{R}^N)$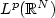 was proved. In this paper, we consider the case of “$q \ge \max\{m+\frac{2}{N},2\}$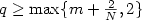 and small $L^{\ell}$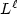 data” with any fixed $\ell \ge \frac{N(q-m)}{2}$ 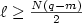and show that (i) there exists a time global solution (u,v) of (KS) and it decays to 0 as t tends to ∞ and (ii) a solution u of the first equation in (KS) behaves like the Barenblatt solution asymptotically as t tends to ∞, where the Barenblatt solution is the exact solution (with self-similarity) of the porous medium equation $u_t = \Delta u^m$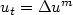 with m>1.