Hostname: page-component-5c6d5d7d68-wbk2r Total loading time: 0 Render date: 2024-08-27T04:32:33.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Moderate deviationsfor two sample t-statistics

Published online by Cambridge University Press:  19 June 2007

Hongyuan Cao
Hongyuan Cao*
Affiliation:
Department of Statistics and Operations Research, University of North Carolina-Chapel Hill, Chapel Hill, NC 27599, USA; hycao@email.unc.edu
Get access

Abstract

Let X1,...,Xn1 be a random sample from a population with mean µ1 and variance $\sigma_1^2$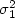, and X1,...,Xn1 be a random sample from another population with mean µ2 and variance $\sigma_2^2$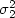 independent of {Xi,1 ≤ i ≤ n1}. Consider the two sample t-statistic $ T={{\bar X-\bar Y-(\mu_1-\mu_2)} \over \sqrt{s_1^2/n_1+s_2^2/n_2}}$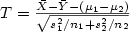. This paper shows that ln P(T ≥ x) ~ -x²/2 for any x := x(n1,n2) satisfying x → ∞, x = o(n1 + n2)1/2 as n1,n2 → ∞ provided 0 < c1 ≤ n1/n2 ≤ c2 < ∞. If, in addition, E|X1|3 < ∞, E|Y1|3 < ∞, then $\frac{P(T \geq x)}{1-\Phi(x)} \to 1 $ holds uniformly in x ∈ (O,o((n1 + n2)1/6))

Keywords

Two sample t-statisticasymptotic distributionmoderate deviation.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 11: Special Issue: "Stochastic analysis and mathematical finance" in honor of Nicole El Karoui's 60th birthdaySpecial Issue: "Stochastic analysis and mathematical finance" in honor of Nicole El Karoui's 60th birthday , June 2007 , pp. 264 - 271
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Giné, E., Gőtze, F., and Mason, D.M., When is the student t-statistic asymptotically standard normal? Ann. Probab. 25 (1997) 1514–1531.
Jing, B.-Y., Shao, Q.M., and Wang, Q.Y., Self-normalized Cramér-type large deviations for independent random variables. Ann. Probab. 31 (2003) 2167–2215.
V.V. Petrov, Limit Theorems of Probability Theory. Clarendon Press, Oxford (1995).
Robinson, J., and Wang, Q., On the self-normalized Cramér-type large deviation. J. Theor. Probab. 18 (2005) 891–909. CrossRef
Shao, Q.M., Self-normalized large deviations. Ann. Probab. 25 (1997) 285–328.
Shao, Q.M., Cramér, A type large deviation result for student's t-statistic. J. Theor. Probab. 12 (1999) 385–398. CrossRef