We consider a diffusion process X which is observed at times i/n for i = 0,1,...,n, each observation being subject to a measurement error. All errors are independent and centered Gaussian with known variance pn. There is an unknown parameter within the diffusion coefficient, to be estimated. In this first paper the case when X is indeed a Gaussian martingale is examined: we can prove that the LAN property holds under quite weak smoothness assumptions, with an explicit limiting Fisher information. 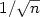What is perhaps the most interesting is the rate at which this convergence takes place: it is $1/\sqrt{n}$ (as when there is no measurement error) when pn goes fast enough to 0, namely npn is bounded. Otherwise, and provided the sequence pn itself is bounded, the rate is (pn / n)1/4. In particular if pn = p does not depend on n, we get a rate n-1/4.