Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-10T21:36:53.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple Fourier analysis for bang-bang controls with memory

Published online by Cambridge University Press:  16 July 2009

Robert L. Sternberg
Robert L. Sternberg
Affiliation:
113 Seneca Drive, Noank, CT, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Bennett functions 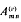, (h, k), defined below and elsewhere, have been used extensively in Fourier analysing the output of certain devices such as rectifiers, limiters and other instantaneous modulators responding to a two-frequency input for which the output at time t depends only on the device input–output characteristic Y = Y(X) and the input at time t. Here, with the aid of a new set of modified Bennett functions 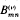, (h, k), these methods are extended to solve the same problems for non-instantaneous bang-bang controls with multivalued input–output characteristics Y = Y(X) and hence having memory.

Type
Research Article
Information
European Journal of Applied Mathematics , Volume 3 , Issue 1 , March 1992 , pp. 75 - 92
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bennett, W. R. 1933 New results in the calculation of modulation products. Bell Syst. Tech. J. 12, 228–243.Google Scholar
[2]Bennett, W. R. 1947 The biased ideal rectifier. Bell Syst. Tech. J. 26, 139–169.Google Scholar
[3]Sternberg, R. L. & Kaufman, H. 1953 A general solution of the two-frequency modulation product problem, I. J. Math. & Phys. 32, 233–242Google Scholar
[4]Sternberg, R. L. 1954 A general solution of the two frequency modulation product problem, II. Tables of the functions (h, k). J. Math. & Phys. 33, 68–79.Google Scholar
[5]Sternberg, R. L. 1954 A general solution of the two frequency modulation product problem, IIIRectifiers and limiters. J. Math. & Phys. 33, 199–205.Google Scholar
[6]Sternberg, R. L., Shipman, J. S. & Thurston, W. B. 1954 Tables of Bennett functions for the two-frequency modulation product problem for the half-wave square-law rectifier. Quart. J. Mech. & Appl. Math. 7 (4), 505–509.Google Scholar
[7]Sternberg, R. L. & Shipman, J. S., Kaufman, H. 1955 Tables of Bennett functions for the two-frequency modulation product problem for the half-wave square-law rectifier. Quart. J. Mech. & Appl. Math. 8, 457–467.Google Scholar
[8]Sternberg, R. L., Shipman, J. S., Zohn, S. R. 1959 Multiple Fourier analysis in rectifier problems. Quart. Appl. Math. 16, 335–360.Google Scholar
[9]Sternberg, R. L., Sheets, M., Sternberg, H. M., Shigematsu, A. & Sternberg, A. L. 1974 Multiple Fourier analysis in rectifier problems II.. Quart. Appl. Math. 31, 293–315.Google Scholar
[10]sternberg, R. L. & Sternberg, H. M. 1976 Backward recurrence relations for Bennett functions. Portugaliae Math. 35, 61–64Google Scholar
[11]Lampard, D. G. 1952 Harmonic intermodulation distortion in power law devices. Proc. IEE IV. 55Google Scholar
[12]Feuerstein, E. 1957 Intermodulation products for v-law biased wave rectifier for multiple frequency input. Quart. Appl. Math. 15, 183–192.Google Scholar
[13]Kaufman, H. 1956 Modulation products in power-law devices. Math. Mag. 29, 9–15.Google Scholar
[14]Montroll, E. W. 1954 Frequency spectrum of vibrations of crystal lattices. Am. Math. Month 61 (11), 46–73.Google Scholar
[15]Shipman, J. S. 1955 On Middleton's Paper-some general results in the theory of noise through non-linear devices. Quart. Appl. Math. 13, 200–201.Google Scholar
[16]Hood, M. J.. On the computation of modified Bennett functions. Euro. J. Appl. Math. 3, 93–95.Google Scholar