Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T14:49:31.323Z Has data issue: false hasContentIssue false
  • English
  • Français

On accurately estimating stability thresholds for periodic spot patterns of reaction-diffusion systems in 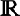$\mathbb{R}$2

Published online by Cambridge University Press:  04 March 2015

D. IRON ,
J. RUMSEY ,
M. J. WARD  and
J. WEI
D. IRON
Affiliation:
Department of Mathematics, Dalhousie University, Halifax, Nova Scotia, B3H 3J5, Canada
J. RUMSEY
Affiliation:
Faculty of Management, Dalhousie University, Halifax, Nova Scotia, B3H 3J5, Canada
M. J. WARD
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, B.C., V6T 1Z2, Canada
J. WEI
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, B.C., V6T 1Z2, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

In the limit of an asymptotically large diffusivity ratio of order 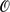$\mathcal{O}$(ϵ−2) ≫ 1, steady-state spatially periodic patterns of localized spots, where the spots are centred at lattice points of a Bravais lattice, are well-known to exist for certain two-component reaction–diffusion systems (RD) in 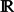$\mathbb{R}$2. For the Schnakenberg RD model, such a localized periodic spot pattern is linearly unstable when the diffusivity ratio exceeds a certain critical threshold. However, since this critical threshold has an infinite-order logarithmic series in powers of the logarithmic gauge ν ≡ −1/log ϵ, a low-order truncation of this series is expected to be in rather poor agreement with the true stability threshold unless ϵ is very small. To overcome this difficulty, a hybrid asymptotic-numerical method is formulated and implemented that has the effect of summing this infinite-order logarithmic expansion for the stability threshold. The numerical implementation of this hybrid method relies critically on obtaining a rapidly converging infinite series representation of the regular part of the Bloch Green's function for the reduced-wave operator. Numerical results from the hybrid method for the stability threshold associated with a periodic spot pattern on a regular hexagonal lattice are compared with the two-term asymptotic results of [10] (Iron et al. J. Nonlinear Science, 2014). As expected, the difference between the two-term and hybrid results is rather large when ϵ is only moderately small. A related hybrid method is devised for accurately approximating the stability threshold associated with a periodic pattern of localized spots for the Gray-Scott RD system in 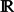$\mathbb{R}$2.

Keywords

singular perturbationslocalized spotssumming logarithmic expansionsBravais latticeFloquet–Bloch theoryGreen's function
Type
Papers
Information
European Journal of Applied Mathematics , Volume 26 , Issue 3 , June 2015 , pp. 325 - 353
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abramowitz, M. & Stegun, I. (1970) Handbook of Mathematical Functions, 9th ed., Dover Publications, New York.Google Scholar
[2]Ashcroft, N. & Mermin, N. (1976) Solid State Physics, Holt, Rinehart and Winston, NC, USA.Google Scholar
[3]Beylkin, G., Kurcz, C. & Monzón, L. (2008) Fast algorithms for Helmholtz Green's functions. Proc. R. Soc. A 464, 3301–3326.CrossRefGoogle Scholar
[4]Chen, X. & Oshita, Y. (2007) An application of the modular function in nonlocal variational problems. Arch. Ration. Mech. Anal. 186 (1), 109–132.CrossRefGoogle Scholar
[5]Chen, W. & Ward, M. J. (2011) The stability and dynamics of localized spot patterns in the two-dimensional Gray-Scott model. SIAM J. Appl. Dyn. Syst. 10 (2), 582–666.CrossRefGoogle Scholar
[6]Doelman, A., Gardner, R. A. & Kaper, T. (2001) Large stable pulse solutions in reaction-diffusion equations. Indiana U. Math. J. 50 (1), 443–507.CrossRefGoogle Scholar
[7]Doelman, A., Gardner, R. A. & Kaper, T. (2002) A stability index analysis of 1-D patterns of the Gray-Scott model. Memoirs of the AMS 155 (737). http://scholar.google.ca/citations?view_op=view_citation&hl=en&user=kB-otT4AAAAJ&citation_for_view=kB-otT4AAAAJ:olpn-zPbctOC.CrossRefGoogle Scholar
[8]Hormozi, S. & Ward, M. J. (2014) A hybrid asymptotic-numerical method for calculating drag coefficients in 2-D low Reynolds number flow. to appear, J. Eng. Math. 30 pp. http://link.springer.com/article/10.1007/s10665-014-9701-x.CrossRefGoogle Scholar
[9]Iron, D., Ward, M. J. & Wei, J. (2001) The stability of spike solutions to the one-dimensional Gierer-Meinhardt model. Physica D 150 (1–2), 25–62.CrossRefGoogle Scholar
[10]Iron, D., Rumsey, J., Ward, M. J. & Wei, J. (2014) Logarithmic expansions and the stability of periodic patterns of localized spots for reaction-diffusion systems in $\mathbb{R}$2. J. Nonlinear Science, 24 (5), 564–627.CrossRefGoogle Scholar
[11]Kolokolnikov, T., Ward, M. J. & Wei, J. (2009) Spot self-replication and dynamics for the Schnakenberg Model in a two-dimensional domain. J. Nonlinear Sci. 19 (1), 1–56.CrossRefGoogle Scholar
[12]Kolokolnikov, T., Titcombe, M. S. & Ward, M. J. (2005) Optimizing the fundamental Neumann eigenvalue for the Laplacian in a domain with small traps. Eur. J. Appl. Math. 16 (2), 161–200.CrossRefGoogle Scholar
[13]Krichever, I. M. (1989) Spectral theory of two-dimensional periodic operators and its applications. Russ. Math. Surv. 44 (2), 145–225.CrossRefGoogle Scholar
[14]Kropinski, M. C., Ward, M. J. & Keller, J. B. (1995) A hybrid asymptotic-numerical method for calculating low Reynolds number flows past symmetric cylindrical bodies. SIAM J. Appl. Math. 55 (6), 1484–1510.CrossRefGoogle Scholar
[15]Kuchment, P. (1993) Floquet Theory for Partial Differential Equations, Birkhauser, Basel.CrossRefGoogle Scholar
[16]Kropinski, M. C., Lindsay, A. & Ward, M. J. (2011) Asymptotic analysis of localized solutions to some linear and nonlinear biharmonic eigenvalue problems. Stud. Appl. Math. 126 (4), 347–408.CrossRefGoogle Scholar
[17]Linton, C. M. (2010) Lattice sums for the Helmholtz equation. SIAM Rev. 52 (4), 630–674.CrossRefGoogle Scholar
[18]Moroz, A. (2006) Quasi-periodic Green's functions of the Helmholtz and Laplace equations. J. Phys. A: Math. Gen. 39 (36), 11247–11282.CrossRefGoogle Scholar
[19]Muratov, C. & Osipov, V. V. (2000) Static spike autosolitons in the Gray-Scott model. J. Phys. A: Math Gen. 33, 8893–8916.CrossRefGoogle Scholar
[20]Muratov, C. & Osipov, V. V. (2001) Spike autosolitons and pattern formation scenarios in the two-dimensional Gray-Scott model. Eur. Phys. J. B 22, 213–221.CrossRefGoogle Scholar
[21]Muratov, C. & Osipov, V. V. (2002) Stability of static spike autosolitons in the Gray-Scott model. SIAM J. Appl. Math. 62 (5), 1463–1487.CrossRefGoogle Scholar
[22]Nishiura, Y. (2002) Far-From Equilibrium Dynamics, Translations of Mathematical Monographs, Vol. 209, AMS Publications, Providence, Rhode Island.CrossRefGoogle Scholar
[23]Piessens, R. (2000) The Hankel transform. In: Poularikas, A. D. (editor), The Transforms and Applications Handbook, 2nd ed., CRC Press LLC, Boca Raton.Google Scholar
[24]Pillay, S., Ward, M. J., Pierce, A. & Kolokolnikov, T. (2010) An asymptotic analysis of the mean first passage time for narrow escape problems: Part I: Two-dimensional domains. SIAM Multiscale Model. Simul. 8 (3), 803–835.CrossRefGoogle Scholar
[25]Rozada, I., Ruuth, S. & Ward, M. J. (2014) The stability of localized spot patterns for the Brusselator on the sphere. SIAM J. Appl. Dyn. Syst. 13 (1), 564–627.CrossRefGoogle Scholar
[26]Van der Ploeg, H. & Doelman, A. (2005) Stability of spatially periodic pulse patterns in a class of singularly perturbed reaction-diffusion equations. Indiana Univ. Math. J. 54 (5), 1219–1301.Google Scholar
[27]Vanag, V. K. & Epstein, I. R. (2007) Localized patterns in reaction-diffusion systems. Chaos 17 (3), 037110.CrossRefGoogle ScholarPubMed
[28]Vladimirov, A. G., McSloy, J. M., Skryabin, D. S. & Firth, W. J. (2002) Two-dimensional clusters of solitary structures in driven optical cavities. Phys. Rev. E 65 046606.CrossRefGoogle ScholarPubMed
[29]Ward, M. J. & Kropinski, M. C. (2010) Asymptotic methods for PDE problems in fluid mechanics and related systems with strong localized perturbations in two dimensional domains. In: Asymptotic Methods in Fluid Mechanics: Surveys and Results. CISM International centre for mechanical science, Vol. 523, pp. 23–70.CrossRefGoogle Scholar
[30]Ward, M. J., Henshaw, W. D. & Keller, J. (1993) Summing logarithmic expansions for singularly perturbed eigenvalue problems. SIAM J. Appl. Math. 53 (3), 799–828.CrossRefGoogle Scholar
[31]Ward, M. J. & Wei, J. (2003) Hopf bifurcations and oscillatory instabilities of spike solutions for the one-dimensional Gierer-Meinhardt model. J. Nonlinear Sci. 13 (2), 209–264.CrossRefGoogle Scholar
[32]Wei, J. (1999) On single interior spike solutions for the Gierer-Meinhardt system: uniqueness and stability estimates. Eur. J. Appl. Math. 10 (4), 353–378.CrossRefGoogle Scholar
[33]Wei, J. & Winter, M. (2001) Spikes for the two-dimensional Gierer-Meinhardt system: The weak coupling case. J. Nonlinear Sci. 11 (6), 415–458.CrossRefGoogle Scholar
[34]Wei, J. & Winter, M. (2003) Existence and stability of multiple spot solutions for the Gray-Scott model in $\mathbb{R}$2. Physica D 176 (3-4), 147–180.CrossRefGoogle Scholar
[35]Wei, J. & Winter, M. (2008) Stationary multiple spots for reaction-diffusion systems. J. Math. Biol. 57 (1), 53–89.CrossRefGoogle ScholarPubMed