Hostname: page-component-7479d7b7d-767nl Total loading time: 0 Render date: 2024-07-10T15:19:59.203Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularity of source-type solutions to the thin-film equation with zero contact angle and mobility exponent between 3/2 and 3

Published online by Cambridge University Press:  22 May 2013

LORENZO GIACOMELLI ,
MANUEL V. GNANN  and
FELIX OTTO
LORENZO GIACOMELLI
Affiliation:
SBAI Department, Sapienza University of Rome, Via Scarpa 16, 00161 Roma, Italy email: lorenzo.giacomelli@sbai.uniroma1.it
MANUEL V. GNANN
Affiliation:
Max Planck Institute for Mathematics in the Sciences, Inselstr. 22, 04103 Leipzig, Germany email: gnann@mis.mpg.de; otto@mis.mpg.de
FELIX OTTO
Affiliation:
Max Planck Institute for Mathematics in the Sciences, Inselstr. 22, 04103 Leipzig, Germany email: gnann@mis.mpg.de; otto@mis.mpg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

In one space dimension, we consider source-type (self-similar) solutions to the thin-film equation with vanishing slope at the edge of their support (zero contact-angle condition) in the range of mobility exponents 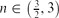$n\in\left(\frac 3 2,3\right)$. This range contains the physically relevant case n=2 (Navier slip). The existence and (up to a spatial scaling) uniqueness of these solutions has been established in [3] (Bernis, F., Peletier, L. A. & Williams, S. M. (1992) Source type solutions of a fourth-order nonlinear degenerate parabolic equation. Nonlinear Anal. 18, 217–234). It is also shown there that the leading-order expansion near the edge of the support coincides with that of a travelling-wave solution. In this paper we substantially sharpen this result, proving that the higher order correction is analytic with respect to two variables: the first one is just the spatial variable whereas the second one is a (generically irrational, in particular for n=2) power of it, which naturally emerges from a linearisation of the operator around the travelling-wave solution. This result shows that – as opposed to the case of n=1 (Darcy) or to the case of the porous medium equation (the second-order analogue of the thin-film equation) – in this range of mobility exponents, source-type solutions are not smooth at the edge of their support even when the behaviour of the travelling wave is factored off. We expect the same singular behaviour for a generic solution to the thin-film equation near its moving contact line. As a consequence, we expect a (short-time or small-data) well-posedness theory – of which this paper is a natural prerequisite – to be more involved than in the case n=1.

Keywords

Self-similar solutionsDegenerate parabolic equationsSmoothness and regularity of solutionsSingular nonlinear boundary value problemsInvariant manifolds
Type
Papers
Information
European Journal of Applied Mathematics , Volume 24 , Issue 5 , October 2013 , pp. 735 - 760
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Angenent, S. (1988) Local existence and regularity for a class of degenerate parabolic equations. Math. Ann. 280 (3), 465–482.Google Scholar
[2]Beretta, E., Bertsch, M. & Dal Passo, R. (1995) Nonnegative solutions of a fourth-order nonlinear degenerate parabolic equation. Arch. Ration. Mech. Anal. 129 (2), 175–200.Google Scholar
[3]Bernis, F., Hulshof, J. & King, John R. (2000) Dipoles and similarity solutions of the thin film equation in the half-line. Nonlinearity 13 (2), 413–439.Google Scholar
[4]Bernis, F., Peletier, L. A. & Williams, S. M. (1992) Source-type solutions of a fourth-order nonlinear degenerate parabolic equation. Nonlinear Anal. 18 (3), 217–234.Google Scholar
[5]Bertozzi, A. L. & Pugh, M. (1996) The lubrication approximation for thin viscous films: Regularity and long-time behavior of weak solutions. Comm. Pure Appl. Math. 49 (2), 85–123.Google Scholar
[6]Bowen, M. & King, J. R. (2001) Asymptotic behaviour of the thin film equation in bounded domains. Eur. J. Appl. Math. 12 (2), 135–157.Google Scholar
[7]Chiricotto, M. & Giacomelli, L. (2011) Droplets spreading with contact-line friction: Lubrication approximation and traveling wave solutions. Commun. Appl. Ind. Math. 2 (2), e-388 (1–16).Google Scholar
[8]Coddington, Earl A. & Levinson, N. (1955) Theory of Ordinary Differential Equations, McGraw-Hill, New York.Google Scholar
[9]Dal Passo, R., Garcke, H. & Grün, G. (1998) On a fourth-order degenerate parabolic equation: Global entropy estimates, existence, and qualitative behavior of solutions. SIAM J. Math. Anal. 29 (2), 321–342 (electronic).CrossRefGoogle Scholar
[10]Daskalopoulos, P. & Hamilton, R. (1998) Regularity of the free boundary for the porous medium equation. J. Am. Math. Soc. 11 (4), 899–965.CrossRefGoogle Scholar
[11]de Gennes, P. G. (Jul. 1985) Wetting: Statics and dynamics. Rev. Mod. Phys. 57, 827–863.CrossRefGoogle Scholar
[12]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007) Source-type solutions of the fourth-order unstable thin film equation. Eur. J. Appl. Math. 18 (3), 273–321.Google Scholar
[13]Ferreira, R. & Bernis, F. (1997) Source-type solutions to thin-film equations in higher dimensions. Eur. J. Appl. Math. 8 (5), 507–524.Google Scholar
[14]Giacomelli, L. & Knüpfer, H. (2010) A free boundary problem of fourth order: Classical solutions in weighted Hölder spaces. Comm. Partial Differ. Equ. 35 (11), 2059–2091.Google Scholar
[15]Giacomelli, L., Knüpfer, H. & Otto, F. (2008) Smooth zero-contact-angle solutions to a thin-film equation around the steady state. J. Differ. Equ. 245 (6), 1454–1506.Google Scholar
[16]Giacomelli, L. & Otto, F. (2003) Rigorous lubrication approximation. Interfaces Free Bound. 5 (4), 483–529.Google Scholar
[17]Grün, G. (2004) Droplet spreading under weak slippage–-existence for the Cauchy problem. Comm. Partial Differ. Equ. 29 (11–12), 1697–1744.Google Scholar
[18]Hartman, P. (2002) Ordinary Differential Equations, Vol. 38, Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA. (Corrected reprint of the second (1982) ed. [Birkhäuser, Boston, MA; MR0658490 (83e:34002)], with a foreword by Peter Bates).Google Scholar
[19]Knüpfer, H. (2011) Well-posedness for the Navier slip thin-film equation in the case of partial wetting. Comm. Pure Appl. Math. 64 (9), 1263–1296.Google Scholar
[20]Koch, H. (1999) Non-Euclidean Singular Intergrals and the Porous Medium Equation, Habilitation thesis, Universität Heidelberg, Heidelberg, Germany.Google Scholar
[21]Oron, A., Davis, Stephen H. & Bankoff, S. G. (Jul. 1997) Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980.Google Scholar
[22]Smyth, N. F. & Hill, J. M. (1988) High-order nonlinear diffusion. IMA J. Appl. Math. 40 (2), 73–86.Google Scholar
[23]Vázquez, J. L. (2007) The Porous Medium Equation, Oxford Mathematical Monographs on Mathematical Theory. Oxford University Press (The Clarendon Press), Oxford, UK.Google Scholar