Hostname: page-component-5c6d5d7d68-pkt8n Total loading time: 0 Render date: 2024-08-11T13:24:46.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock waves and compactons for fifth-order non-linear dispersion equations

Published online by Cambridge University Press:  12 November 2009

VICTOR A. GALAKTIONOV
VICTOR A. GALAKTIONOV*
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK email: vag@maths.bath.ac.uk; masvg@bath.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The following first problem is posed: 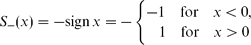is a correct ‘entropy solution’ of the Cauchy problem for the fifth-order degenerate non-linear dispersion equations (NDEs), same as for the classic Euler one ut + uux = 0, These two quasi-linear degenerate partial differential equations (PDEs) are chosen as typical representatives; so other (2m + 1)th-order NDEs of non-divergent form admit such shocks waves. As a related second problem, the opposite initial shock S+(x) = −S−(x) = sign x is shown to be a non-entropy solution creating a rarefaction wave, which becomes C∞ for any t > 0. Formation of shocks leads to non-uniqueness of any ‘entropy solutions’. Similar phenomena are studied for a fifth-order in time NDE uttttt = (uux)xxxx in normal form.

On the other hand, related NDEs, such as 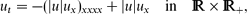are shown to admit smooth compactons, as oscillatory travelling wave solutions with compact support. The well-known non-negative compactons, which appeared in various applications (first examples by Dey, 1998, Phys. Rev. E, vol. 57, pp. 4733–4738, and Rosenau and Levy, 1999, Phys. Lett. A, vol. 252, pp. 297–306), are non-existent in general and are not robust relative to small perturbations of parameters of the PDE.

Type
Papers
Information
European Journal of Applied Mathematics , Volume 21 , Issue 1 , February 2010 , pp. 1 - 50
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bressan, A. (2000) Hyperbolic Systems of Conservation Laws. The One Dimensional Cauchy Problem, Oxford University Press, Oxford.CrossRefGoogle Scholar
[2]Cai, H. (1997) Dispersive smoothing effects for KdV type equations. J. Differ. Eq. 136, 191–221.CrossRefGoogle Scholar
[3]Christodoulou, D. (2007) The Euler equations of compressible fluid flow. Bull. Amer. Math. Soc. 44, 581–602.CrossRefGoogle Scholar
[4]Clarkson, P. A., Fokas, A. S. & Ablowitz, M. (1989) Hodograph transformastions of linearizable partial differential equations. SIAM J. Appl. Math. 49, 1188–1209.CrossRefGoogle Scholar
[5]Coclite, G. M. & Karlsen, K. H. (2006) On the well-posedness of the Degasperis–Procesi equation. J. Funct. Anal. 233, 60–91.CrossRefGoogle Scholar
[6]Costin, O. & Tanveer, S. (2006) Complex singularity analysis for a nonlinear PDE. Comm. Part. Diff. Eq. 31, 593–637.CrossRefGoogle Scholar
[7]Craig, W. & Goodman, J. (1990) Linear dispersive equations of Airy type. J. Diff. Eq. 87, 38–61.CrossRefGoogle Scholar
[8]Craig, W., Kappeler, T. & Strauss, W. (1992) Gain of regularity for equations of KdV type. Ann. Inst. H. Poincare 9, 147–186.CrossRefGoogle Scholar
[9]Da Prato, G. & Grisvard, P. (1979) Equation d'évolutions abstraites de type parabolique. Ann. Mat. Pura Appl. 4 (120), 329–396.CrossRefGoogle Scholar
[10]Dafermos, C. (1999) Hyperbolic Conservation Laws in Continuum Physics, Springer, Berlin.Google Scholar
[11]Dawson, L. L. (2007) Uniqueness properties of higher order dispersive equations. J. Diff. Eq. 236, 199–236.CrossRefGoogle Scholar
[12]Dey, B. (1998) Compacton solutions for a class of two parameter generalized odd-order Korteweg–de Vries equations, Phys. Rev. E 57, 4733–4738.CrossRefGoogle Scholar
[13]Egorov, Yu. V., Galaktionov, V. A., Kondratiev, V. A. & Pohozaev, S. I. (2004) Asymptotic behaviour of global solutions to higher-order semilinear parabolic equations in the supercritical range. Adv. Diff. Eq. 9, 1009–1038.Google Scholar
[14]Escher, J., Liu, Y. & Yin, Z. (2007) Shock waves and blow-up phenomena for the periodic Degasperis–Procesi equation. Indiana Univ. Math. J. 56, 87–117.CrossRefGoogle Scholar
[15]Escher, J. & Prokert, G. (2006) Analyticity of solutions to nonlinear parabolic equations on manifolds and an application to Stokes flow. J. Math. Fluid Mech. 8, 1–35.CrossRefGoogle Scholar
[16]Faminskii, A. V. (2002) On the mixed problem for quasilinear equations of the third order. J. Math. Sci. 110, 2476–2507.CrossRefGoogle Scholar
[17]Galaktionov, V. A. (2007) Sturmian nodal set analysis for higher-order parabolic equations and applications. Adv. Diff. Eq. 12, 669–720.Google Scholar
[18]Galaktionov, V. A. (2008) Nonlinear dispersive equations: Smooth deformations, compactons, and extensions to higher orders. Comput. Math. Math. Phys. 48, 1823–1856. Arχiv:0902.0275.CrossRefGoogle Scholar
[19]Galaktionov, V. A. (2009) On regularity of a boundary point in higher-order parabolic equations: a blow-up approach. NoDEA. 16, 597–655. Arχiv:0901.3986.CrossRefGoogle Scholar
[20]Galaktionov, V. A. On single point gradient blow-up and nonuniqueness for a third-order nonlinear dispersion equation. J. Evol. Equat. Submitted. Arχiv:0902.1635.Google Scholar
[21]Galaktionov, V. A., Mitidieri, E. & Pohozaev, S. I. (2009) Variational approach to complicated similarity solutions of higher-order nonlinear evolution equations of parabolic, hyperbolic, and nonlinear dispersion types, In: Maz’ya, V. (editor), Sobolev Spaces in Mathematics: II; Application in Analysis and Partial Differential Equations, International Mathematical Series, Vol. 9, Springer, New York. Arχiv:0902.1425.Google Scholar
[22]Galaktionov, V. A. & Pohozaev, S. I. (2008) Third-order nonlinear dispersive equations: Shocks, rarefaction, and blow-up waves. Comput. Math. Math. Phys. 48, 1784–1810. Arχiv:0902.0253.CrossRefGoogle Scholar
[23]Galaktionov, V. A. & Svirshchevskii, S. R. (2007) Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics, Chapman & Hall/CRC, Boca Raton, FL.Google Scholar
[24]Gazzola, F. & Grunau, H.-C. (2006) Radial entire solutions for supercritical biharmonic equations. Math. Ann. 334, 905–936.CrossRefGoogle Scholar
[25]Gel’fand, I. M. (1963) Some problems in the theory of quasilinear equations. Amer. Math. Soc. Trans. 29 (2), 295–381.Google Scholar
[26]Hoshiro, T. (1999) Mouree's method and smoothing properties of dispersive equations. Comm. Math. Phys. 202, 255–265.CrossRefGoogle Scholar
[27]Hyman, J. M. & Rosenau, P. (1998) Pulsating multiplet solutions of quintic wave equations. Phys. D 123, 502–512.CrossRefGoogle Scholar
[28]Inc, M. (2007) New compacton and solitary pattern solutions of the nonlinear modified dispersive Klein–Gordon equations. Chaos Solit. Fract. 33, 1275–1284.CrossRefGoogle Scholar
[29]Kawamoto, S. (1985) An exact transformation from the Harry Dym equation to the modified KdV equation. J. Phys. Soc. Jpn 54, 2055–2056.CrossRefGoogle Scholar
[30]Kruzhkov, S. N. (1970) First-order quasilinear equations in several independent variables. Math. USSR Sbornik 10, 217–243.CrossRefGoogle Scholar
[31]Landmark, H. (2007) Formation and dynamics of shock waves in the Degasperis–Procesi equation. J. Nonlin. Sci. 17, 169–198.CrossRefGoogle Scholar
[32]Levandosky, J. L. (2001) Smoothing properties of nonlinear dispersive equations in two spatial dimensions. J. Diff. Eq. 175, 275–372.CrossRefGoogle Scholar
[33]Lunardi, A. (1995) Analytic Semigroups and Optimal Regularity in Parabolic Problems, Birkhäuser, Basel/Berlin.Google Scholar
[34]Naimark, M. A. (1968) Linear Differential Operators, Part I, Ungar, New York.Google Scholar
[35]Oleinik, O. A. (1963) Discontinuous solutions of non-linear differential equations. Amer. Math. Soc. 26 (2), 95–172.Google Scholar
[36]Oleinik, O. A. (1963) Uniqueness and stability of the generalized solution of the Cauchy problem for a quasi-linear equation. Amer. Math. Soc. Trans. 33 (2), 285–290.Google Scholar
[37]Perko, L. (1991) Differential Equations and Dynamical Systems, Springer, New York.CrossRefGoogle Scholar
[38]Poisson, D. (1808) Mémoire sur la théorie du son. J. Polytech. (14 éme cahier) 7, 319–392.Google Scholar
[39]Pomeau, Y., Le Berre, M., Guyenne, P. & Grilli, S. (2008) Wave-breaking and generic singularities of nonlinear hyperbolic equations. Nonlinearity 21, T61–T79.CrossRefGoogle Scholar
[40]Porubov, A. V. & Velarde, M. G. (2002) Strain kinks in an elastic rod embedded in a viscoelastic medium. Wave Mot. 35, 189–204.CrossRefGoogle Scholar
[41]Riemann, B. (1858–1959) Über die Fortpfanzung ebener Luftwellen von endlicher Schwingungswete, Abhandlung. Gesellshaft Wissenshaft. Göttingen, Math.-Phys. Klasse, 8, 43.Google Scholar
[42]Rosenau, P. (1994) Nonlinear dispersion and compact structures. Phys. Rev. Lett. 73, 1737–1741.CrossRefGoogle ScholarPubMed
[43]Rosenau, P. (1996) On solitons, compactons, and Lagrange maps. Phys. Lett. A 211, 265–275.CrossRefGoogle Scholar
[44]Rosenau, P. (1998) On a class of nonlinear dispersive-dissipative interactions. Phys. D 123, 525–546.CrossRefGoogle Scholar
[45]Rosenau, P. (2000) Compact and noncompact dispersive patterns, Phys. Lett. A 275, 193–203.CrossRefGoogle Scholar
[46]Rosenau, P. & Hyman, J. M. (1993) Compactons: Solitons with finite wavelength. Phys. Rev. Lett., 70, 564–567.CrossRefGoogle ScholarPubMed
[47]Rosenau, P. & Kamin, S. (1983) Thermal waves in an absorbing and convecting medium. Physica. D 8, 273–283.CrossRefGoogle Scholar
[48]Rosenau, P. & Levy, D. (1999) Compactons in a class of nonlinearly quintic equations. Phys. Lett. A 252, 297–306.CrossRefGoogle Scholar
[49]Smoller, J. (1983) Shock Waves and Reaction–Diffusion Equations, Springer, New York.CrossRefGoogle Scholar
[50]Takuwa, H. (2006) Microlocal analytic smoothing effects for operators of real principal type. Osaka J. Math., 43, 13–62.Google Scholar
[51]Tao, T. (2000) Multilinear weighted convolution of L 2 functions, and applications to nonlinear dispersive equations. Amer. J. Math. 6, 839–908.Google Scholar
[52]Taylor, M. E. (1996) Partial Differential Equations III: Nonlinear Equations, Springer, New York.CrossRefGoogle Scholar
[53]Yan, Z. (2003) Constructing exact solutions for two-dimensional nonlinear dispersion Boussinesq equation II. Solitary pattern solutions. Chaos Solit. Fract. 18, 869–880.CrossRefGoogle Scholar
[54]Yao, R.-X. & Li, Z.-B. (2004) Conservation laws and new exact solutions for the generalized seventh order KdV equation. Chaos Solit. Fract. 20, 259–266.Google Scholar