Hostname: page-component-7479d7b7d-t6hkb Total loading time: 0 Render date: 2024-07-09T19:23:54.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Source-type solutions of the fourth-order unstable thin film equation

Published online by Cambridge University Press:  01 June 2007

J. D. EVANS ,
V. A. GALAKTIONOV  and
J. R. KING
J. D. EVANS
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK email: masjde@maths.bath.ac.uk
V. A. GALAKTIONOV
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK email: vag@maths.bath.ac.uk
J. R. KING
Affiliation:
Theoretical Mechanics Section, University of Nottingham, Nottingham NG7 2RD, UK email: john.king@nottingham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

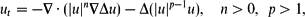We consider the fourth-order thin film equation (TFE) with the unstable second-order diffusion term. We show that, for the first critical exponent 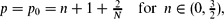where N ≥ 1 is the space dimension, the free-boundary problem the with zero contact angle and zero-flux conditions admits continuous sets (branches) of self-similar similarity solutions of the form 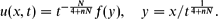For the Cauchy problem, we describe families of self-similar patterns, which admit a regular limit as n → 0+ and converge to the similarity solutions of the semilinear unstable limit Cahn-Hilliard equation 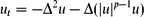studied earlier in [12]. Using both analytic and numerical evidence, we show that such solutions of the TFE are oscillatory and of changing sign near interfaces for all n ∈ (0,nh), where the value 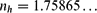characterizes a heteroclinic bifurcation of periodic solutions in a certain rescaled ODE. We also discuss the cases p ⧧ = p0, the interface equation, and regular analytic approximations for such TFEs as an approach to the Cauchy problem.

Type
Papers
Information
European Journal of Applied Mathematics , Volume 18 , Issue 3 , June 2007 , pp. 273 - 321
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Amann, H. (1995) Linear and Quasilinear Parabolic Problems, Volume I: Abstract Linear Theory, Birkhäuser, Basel.Google Scholar
[2]Amann, H. & Escher, J. (1996) Strong continuous dual semigroups, Ann. Mat. Pura Appl., CLXXI, 41–62.Google Scholar
[3]Berger, M. (1977) Nonlinearity and Functional Analysis, Acad. Press, New York.Google Scholar
[4]Bernis, F. & Friedman, A. (1990) Higher order nonlinear degenerate parabolic equations, J. Differ. Equat., 83, 179–206.CrossRefGoogle Scholar
[5]Bernis, F. & McLeod, J. B. (1991) Similarity solutions of a higher order nonlinear diffusion equation, Nonl. Anal. 17, 1039–1068.Google Scholar
[6]Bernis, F., Peletier, L. A. & Williams, S. M. (1992) Source type solutions of a fourth order nonlinear degenerate parabolic equation, Nonl. Anal., TMA, 18, 217–234.Google Scholar
[7]Budd, C. & Galaktionov, V. (1998) Stability and spectra of blow-up in problems with quasi-linear gradient diffusivity, Proc. Roy. Soc. London A, 454, 2371–2407.CrossRefGoogle Scholar
[8]Coddington, E. A. & Levinson, N., Theory of Ordinary Differential Equations, McGraw-Hill Book Company, Inc., New York/London, 1955.Google Scholar
[9]Eidelman, S. D. (1969) Parabolic Systems, North-Holland Publ. Comp., Amsterdam/London.Google Scholar
[10]Evans, J. D., Galaktionov, V. A. & King, J. R., Unstable sixth-order thin film equation. I. Blow-up similarity solutions; II. Global similarity patterns, Nonlinearity, to appear.Google Scholar
[11]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007) Blow-up similarity solutions of the fourth-order unstable thin film equation, Euro J. Appl. Math., 18, 195–231.Google Scholar
[12]Evans, J. D., Galaktionov, V. A. & Williams, J. F. (2006) Blow-up and global asymptotics of the limit unstable Cahn-Hilliard equation, SIAM J. Math. Anal., 38, 64–102.Google Scholar
[13]Ferreira, R. & Bernis, F. (1997) Source-type solutions to thin-film equations in higher dimensions,Euro J. Appl. Math., 8, 507–534.Google Scholar
[14]Friedman, A. (1983) Partial Differential Equations, Robert E. Krieger Publ. Comp., Malabar.Google Scholar
[15]Galaktionov, V. A. (2004) Geometric Sturmian Theory of Nonlinear Parabolic Equations and Applications, Chapman & Hall/CRC, Boca Raton, Florida.Google Scholar
[16]Galaktionov, V. A. (2006) On interfaces and oscillatory solutions of higher-order semilinear parabolic equations with nonlipschitz nonlinearities, Stud. Appl. Math., 117, 353–389.Google Scholar
[17]Galaktionov, V. A. & Svirshchevskii, S. R. (2007) Exact Solution and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics, Chapman & Hall/CRC, Boca Raton, Florida.Google Scholar
[18]Kath, W. L. & Cohen, D. S. (1982) Waiting-time behaviour in a nonlinear diffusion equation, Stud. Appl. Math., 67, 79–105.Google Scholar
[19]King, J. R. (1989) The isolation oxidation of silicon – The reaction-controlled case, SIAM J. Appl. Math., 49, 1064–1080.Google Scholar
[20]King, J. R. (1991) Integral results for nonlinear diffusion equations, J. Engr. Math., 25, 191–205.Google Scholar
[21]King, J. R. & Bowen, M. (2001) Moving boundary problems and non-uniqueness for the thin film equation, Euro J. Appl. Math., 12, 321–356.Google Scholar
[22]Krasnosel'skii, M. A. & Zabreiko, P. P. (1984) Geometrical Methods of Nonlinear Analysis, Springer-Verlag, Berlin/Tokyo.Google Scholar
[23]vonMises, R. Mises, R. (1927) Bemerkungen zur Hydrodynamik, ZAMM, 7, 425–531.Google Scholar
[24]Naimark, M. A. (1968) Linear Differential Operators, Part II, Frederick Ungar Publ. Co., New York.Google Scholar
[25]Perko, L. (1991) Differential Equations and Dynamical Systems, Springer-Verlag, New York.Google Scholar
[26]Smoller, J., Shock Waves and Reaction-Diffusion Equations, Springer-Verlag, New York/Berlin, 1983.CrossRefGoogle Scholar
[27]Smyth, N. F. & Hill, J. M. (1988) High-order nonlinear diffusion, IMA J. Appl. Math., 40, 73–86.CrossRefGoogle Scholar
[28]Vainberg, M. A. & Trenogin, V. A., Theory of Branching of Solutions of Non-Linear Equations, Noordhoff Int. Publ., Leiden, 1974.Google Scholar
[29]Wu, Z., Zhao, J., Yin, J. & Li, H. (2001) Nonlinear Diffusion Equations, World Scientific Publ. Co., Inc., River Edge, NJ.CrossRefGoogle Scholar