Media summary: New models of social norms applied to footbinding, genital cutting, college students drinking, pro-environment behaviours
The expression of the wishes and judgment of the members of the same community … serves … as a most important secondary guide of conduct, in aid of the social instincts, but sometimes in opposition to them. (Darwin, Reference Darwin1871, p. 99)
Humans live in a sea of social norms that govern pretty much all aspects of their lives. (Tomasello, Reference Tomasello, Gelfand, Chiu and Hong2011, p. 20)
Culturally transmitted social norms are an essential factor in human social behaviour (Wrong, Reference Wrong1961; Axelrod, Reference Axelrod1986; Grusec & Kuczynski, Reference Grusec and Kuczynski1997; Richerson et al., Reference Richerson, Baldini, Bell, Demps, Frost, Hillis and Zefferman2016; Lapinski & Rimal, Reference Lapinski and Rimal2005; Bicchieri, Reference Bicchieri2006; Henrich & Ensminger, Reference Henrich, Ensminger, Ensminger and Henrich2014; Fehr & Schurtenberger, Reference Fehr and Schurtenberger2018). Humans learn norms from parents, through educational and religious practices, and from friends and acquaintances, books and media. The ability to learn social norms appears early in child development universally across societies (House et al., Reference House, Kanngiesser, Barrett, Broesch, Cebioglu, Crittenden and Silk2019). The adherence to norms is reinforced by the approval of individuals who follow them and (the threat of) punishment of norm violators. Following norms of a particular group is a way to maintain and enhance one's social identity (Tajfel & Turner, Reference Tajfel, Turner and Worchel1979). Social norms are a foundation of well-functioning communities and the glue that keeps society together. They vary dramatically between different groups (Gelfand et al., Reference Gelfand, Raver, Nishii, Leslie, Lun, Lim and Yamaguchi2011); there is also substantial variation in their effects on individuals within groups (Atran & Ginges, Reference Atran and Ginges2013). Certain norms are internalized, that is, acting according to a norm becomes an end in itself rather than merely a tool in achieving certain goals or avoiding social sanctions (Henrich & Ensminger, Reference Henrich, Ensminger, Ensminger and Henrich2014; Gavrilets & Richerson, Reference Gavrilets and Richerson2017). For individuals who have strongly internalized a norm, violating it is psychologically painful even if the direct material benefits for the violation are positive (Mu et al., Reference Mu, Kitayama, Han and Gelfand2015). Such individuals will also tend to criticize or punish norm violators (Cooter, Reference Cooter2000). Many individuals and groups are willing to pay extremely high costs to enact, defend or promulgate norms that they consider important (Atran & Ginges, Reference Atran and Ginges2013). At the same time, virtually all norms can be violated by individuals under some conditions (e.g. if the costs of compliance are too high; Lapinski et al., Reference Lapinski, Kerr, Zhao and Shupp2017). Society's norms are affected by historical and environmental factors, with some societies being more successful than others owing to their norms and institutions (Morris, Reference Morris2015; Turchin, Reference Turchin2016). Some norms are very stable while others can change rapidly. Understanding the emergence, persistence and effects of social norms, values and beliefs is vital not only from a fundamental research perspective but also for implementing various policies aiming to improve human life.
The concept of social norms varies across disciplines (Bicchieri, Reference Bicchieri2006; Young, Reference Young, Durlauf and Blume2008, Reference Young2015; Nyborg, Reference Nyborg2018). In social psychology, the two most common definitions are those of the descriptive and injunctive norms (Cialdini et al., Reference Cialdini, Reno and Kallgren1990). Descriptive norms involve perceptions of which behaviours are typically performed and what people actually do. In contrast, injunctive norms are behaviours that one is expected to follow and expects others to follow in a given social situation, that is, they refer to what people ought to do even if doing so is against their immediate interests. Injunctive norms are viewed as being sustained by the threat of social disapproval/punishment for norm violations and/or by norm internalization (Bicchieri, Reference Bicchieri2006). This makes them different from ‘conventions’ (Lewis, Reference Lewis1969) for which there is a continuity between the individual's self-interest and the interests of the community that supports the convention (Bicchieri, Reference Bicchieri2006; Young, Reference Young, Durlauf and Blume2008).
Game theory and evolutionary game theory, which are the most appropriate theoretical frameworks for studying social interactions, focus almost exclusively on descriptive norms and conventions. In standard evolutionary game theory approaches to norms (e.g. Young, Reference Young2015), one starts with a population of interacting players who initially use different strategies/actions. The players update their strategies/actions attempting to maximize the payoffs. In the deterministic limit, the population then converges to a locally stable equilibrium (often one of several possible) at which everybody uses the same strategy – a norm. [According to Young (Reference Young1998, p. 821), a norm ‘is, in short, an equilibrium of a game.’] Metaphorically (and mathematically, if one uses the replicator equation for modelling the dynamics) a norm then is just a strategy that has won a competition with other strategies. With stochasticity added, there will be some distribution of strategies around a particular mean strategy.
Such approaches however are not directly applicable for modelling injunctive norms as they do not consider explicitly human expectations about approval, disapproval or punishment, or internalized values of certain acts. They also usually neglect heterogeneity between individuals in their internal values or sensitivity to (dis)approval by others. However, all of these characteristics and properties have been demonstrated to be important in human decision-making (Chung & Rimal, Reference Chung and Rimal2016; Shulman et al., Reference Shulman, Rhodes, Davidson, Ralston, Borghetti and Morr2017) and must be considered when planning and implementing social policies targeting certain types of behaviour.
There are exceptions though. For example, ‘threshold models’ allow for heterogeneity between individuals in how their decision-making is affected by previous actions of others (e.g. Rashevsky Reference Rashevsky1949, Reference Rashevsky1951, Reference Rashevsky1965a, Reference Rashevsky1965b; Granovetter, Reference Granovetter1978; Neary & Newton, Reference Neary and Newton2017; Efferson et al., Reference Efferson, Vogt and Fehr2020). Akerlof (Reference Akerlof1980) explicitly considers reputation and the loss of utility owing to disobeying a code of honour. Bernheim (Reference Bernheim1994) allows for a normative value of status. Azar (Reference Azar2004) and Akcay and van Cleve (Reference Akcay, van Cleve, Wilczynski and Brosnan2020) consider a normative value of conformity with the most common behaviour, and Gavrilets and Richerson (Reference Gavrilets and Richerson2017) and Nyborg (Reference Nyborg2018) include the value of social approval by others in their models of social norms. Here I will follow and extend this approach.
Below, using recent advances in cultural evolution theory, I will build a simple general mathematical framework describing the dynamics of injunctive social norms. I will explicitly account for normative values of certain behaviours, for the effects of passive or active approval and disapproval by others, and for heterogeneity of individuals with respect to normative values and beliefs. I will do so by integrating the classical Schelling–Granovetter model of collective behaviour (Schelling, Reference Schelling1971; Granovetter, Reference Granovetter1978) with a recent approach by Gavrilets and Richerson (Reference Gavrilets and Richerson2017) to modelling social norm internalization. The Schelling–Granovetter model explicitly accounts for heterogeneity between individuals in their reaction to groupmates’ behaviour. This model has been applied to a number of ‘behavioural contagion’ phenomena including residential segregation and mass protests. The Gavrilets–Richerson model explicitly accounts for both material and normative effects on human behaviour, for within-group heterogeneity in these effects and for errors in human decision-making. Gavrilets and Richerson (Reference Gavrilets and Richerson2017) showed how the ability to internalize norms can evolve on evolutionary, i.e. macro, timescales. Here instead I will assume that this ability is already present and that the behaviour of individuals is already affected by certain normative values and costs they assign to certain acts or situations.
Specifically, I will study the dynamics of human behaviour in heterogeneous groups on relatively short time-scales during which the distribution of normative values in the group is approximately stable. My focus will be on two questions that are very important from both theoretical and practical perspectives: how do interactions of material factors, normative values and the expectation of (dis)approval or punishment by others affect individual and group behaviour, and how one can leverage our knowledge about these interactions to achieve certain social goals. In spite of their simplicity, my models exhibit rich dynamics which I study using both analytical approximations and numerical bifurcation analysis. I will illustrate the applicability and generality of my approach by using several examples of successful and unsuccessful attempts to modify social norms in various target populations.
Results
Models
I will consider two different types of models. The models of ‘passive disapproval’ show how norms can be maintained merely by the expectation that norm violators are disapproved by others. In models of ‘passive and active disapproval’, I add costly acts of disapproval and punishment. In both cases, I will focus on the joint effects of material and normative consequences of different acts while allowing for heterogeneity between individuals. I will keep the mathematical complexity of the model at a minimum.
Passive disapproval of norm violators
Consider a very common situation: you need to cross the street, there are no cars or police around, but the crosswalk sign says ‘don't walk’ and there are several people waiting for it to change. You know you are supposed to wait. You also expect that if you break the norm and cross the street, the bystanders will likely disapprove of you. However, you are in a rush. What do you do?
To approach this question theoretically, consider a focal individual who can either follow the injunctive norm and wait for the crosswalk light to turn green (x = 1) or jaywalk (x = 0). [In the models below, an injunctive norm is a behaviour to which at least some individuals assign some positive normative value.] Let b be the expected net material benefit of crossing the street rather than waiting. (The parameter b can also account for a cost of being observed by the police or being hit by a car when jaywalking.) Let v + be an intrinsic benefit of following the norm and v − the intrinsic cost of violating it. The net normative value v = v + + v − can be viewed as the strength of norm internalization (Gavrilets & Richerson, Reference Gavrilets and Richerson2017). Let p be the focal individual's estimate of the frequency of such people, e.g. based on previous observations. I posit that an individual violating the norm assumes that others who do follow it disapprove of his behaviour if they observe it (Fehr & Schurtenberger, Reference Fehr and Schurtenberger2018). The anticipated disapproval imposes an internal psychic cost on the norm violator even if the disapproval carries no direct cost. Assuming that this psychic cost increases with the anticipated number of people who disapprove, I define it as κp, where parameter κ is the maximum normative cost of passive disapproval by others. Then the utility of following the norm is u 1 = v + while that of violating it is u 0 = b − v − − κp. The individual is predicted to comply with the norm if u 1 > u 0 which is equivalent to a condition that their normative value v > v* where a threshold v* for compliance is
Note that an individual with a low normative value v relative to the potential material benefit b will still comply with the norm if the expected normative cost of disapproval κp is high enough. The latter increases with the estimated frequency p of people following the norm.
Consider now a population of individuals repeatedly and simultaneously facing the same dilemma. If all individuals are identical in their material and normative values and costs b, v, κ and everybody is able to estimate the previous frequency p of norm-compliant types and utilities u without errors, everybody will make the same decision and the population will move to a state with p = 0 or p = 1 in just one step. That is, the norm will not be obeyed at all or everybody will comply.
Naturally, individuals in the population can differ in b, v, κ, and their estimates of p. Let the normative value of compliance v have a certain distribution in the population with the corresponding cumulative distribution function (c.d.f.) F (z). For now, assume that all individuals have exactly the same values of b and κ and are able to estimate p precisely. Given b, κ and p, the frequency of individuals with v < v*, who, thus, will not comply, is F (v*). Therefore, the frequency of individuals who will choose to comply with the norm is
Recursive equation (2) describes the dynamics of p in the population. Frequency p always evolves to an equilibrium. The equilibrium values of p can be found from the equality p* = 1 −F (b −κp*). There can be several equilibria and which one is eventually approached depends on initial conditions. An equilibrium p* is locally stable if κf (b − κp*) < 1 and is unstable otherwise. Here f is the probability density function corresponding to F (i.e. f = dF/dv). Given a specific c.d.f. F, one can study the corresponding dynamics analytically, graphically or numerically. A particularly illuminating method, which I will use below, is to plot ‘bifurcation diagrams’ which summarize the dependence of equilibria and their stability of parameters and initial conditions.
Uniform distribution of v. Assume first that v has a uniform distribution between 0 and v max. Assume also that b > v max (so that no one is willing to comply if nobody else is doing it, i.e. if p = 0) and that κ > b (so that, everyone complies if everybody else is complying, i.e. p = 1). Then there is a threshold initial frequency $\tilde{p} = {{{b-v}_{max}} \over {\kappa v_{max}}}$![]() , and the population will converge to a state where the norm is lost (i.e. p → 0) if the initial frequency of compliance p < p̃, but it will ‘fix’ it (i.e. p → 1) if p > p̃ (see the Supplementary Information, SI). Decreasing the normative cost of disapproval κ or increasing material benefit b of not complying decreases p̃ and makes fixing the norm easier. In this model, the population quickly becomes homogeneous in its behaviour in spite of substantial variation in individual preferences.
, and the population will converge to a state where the norm is lost (i.e. p → 0) if the initial frequency of compliance p < p̃, but it will ‘fix’ it (i.e. p → 1) if p > p̃ (see the Supplementary Information, SI). Decreasing the normative cost of disapproval κ or increasing material benefit b of not complying decreases p̃ and makes fixing the norm easier. In this model, the population quickly becomes homogeneous in its behaviour in spite of substantial variation in individual preferences.
Log–normal distribution of v. Alternatively, assume that the distribution of v is log–normal with mean v and variance σ 2 (see the SI). One cannot find the equilibria of equation (2) and check their stability explicitly but it is straightforward to do it numerically.
Figure 1 shows the corresponding equilibrium values of p for different values of the average normative value v̅, normative cost κ and standard deviation σ. [In the terminology of the dynamical systems theory (e.g. Glendinning, Reference Glendinning1994), each subgraph in this figure is a ‘bifurcation diagram’ with σ being a ‘bifurcation parameter’.] The graphs show that the norm can be stably maintained at high frequencies and that the system can have up to two locally stable equilibria separated by an unstable one. Multiple equilibria seem to appear if v̅ + κ > b > v̅ and σ is small enough. Even with a high average normative value of compliance v̅, the population can still be at the no-norm state (e.g. top row, right, where v̅ = 0.9, but p is close to 0). Alternatively, even with a low average normative value v̅ the population can still exhibit high compliance (e.g. the bottom row, left, where v̅ = 0.4, but p is close to 1). The stability of these equilibria is assured by the self-fulfilling expectation of disapproval by the majority of others. Increasing standard deviation σ increases the norm frequency p if v̅ is low, but can decrease it when v̅ is large. Increasing the normative cost κ of (passive) disapproval increases the likelihood of multiple equilibria. Figures S2 and S3 in the SI explore the dependence of equilibrium values of p on v̅ and κ in more details.

Figure 1. Equilibrium values of frequency p for the model with passive disapproval of norm violators (predicted by equation (2)) when the distribution of v in the group is lognormal with mean v̅ and standard deviation σ. Different columns correspond to different values of v̅. Different rows correspond to different values of the maximum cost of disapproval κ. Standard deviation σ is used as the bifurcation parameter. Filled diamonds are stable equilibria. Open diamonds are unstable equilibria separating the two stable ones. Parameter b is set to 1 without loss of generality.
The location and stability of equilibria also depend on the shape of the distribution of v in the population. Figures S4–S6 in the SI show the corresponding bifurcation diagrams for three additional distributions of v: a normal distribution, a Laplace distribution and a logistic distribution, respectively. Although the overall patterns are similar, the specific values of parameters at which the structure of equilibria change can be different.
All four distributions of v considered so far were unimodal. Figure S7 in the SI corresponds to a bimodal distribution of v which may describe a situation when the focal population is a mix of two subgroups with different distributions of normative values. Note that bimodal distributions of normative values within a single population was predicted in Gavrilets and Richerson's (Reference Gavrilets and Richerson2017) evolutionary model while Kimbrough and Vostroknutov (Reference Kimbrough and Vostroknutov2016) demonstrated it empirically in an experimental economic game. In the case of bimodal distributions there can be up to three simultaneously stable equilibria. When the two subgroups are close to each other in their values, the structure of equilibria is naturally similar to that when the distribution of v is unimodal. At intermediate distances between the two subgroups and small σ, there appears a new equilibrium close to p = 0.5. At larger distances, the range of existence and stability of this equilibrium greatly expands while those of equilibria with small and large p shrink. Convergence to equilibria is typically quite fast – a few time steps – as illustrated in Figures S8–S10 in the SI.
Several conclusions emerge from these analyses:
• Unpopular norms (i.e. norms with low v̅) can be stably maintained in the population whereas generally preferred norms (i.e. norms with high v̅) can be present at very low frequencies. Both these outcomes are related to a notion of ‘preference falsification’ (i.e. the act of communicating a preference and/or performing an action that differs from one's true preference under perceived social pressure, Kuran (Reference Kuran1989)).
• Parameters and initial conditions have strong effects on the eventual population state. This implies that different groups can diverge in their state even if they are subject to similar social forces. Also important is the shape of the distribution of individual values/beliefs in the population. Predicting the population social dynamics requires a good knowledge of this distribution.
• All this means that different groups/cities/communities may find themselves at different equilibria owing to differences in initial conditions even if everything else is the same. Moreover, groups/cities/communities can differ in parameter values (costs, benefits, etc.) and in the distribution of normative values. These differences will affect the outcomes of social dynamics.
• The variance σ 2 of the distribution of normative values has nonlinear effects on the frequency of norm-abiding behaviour p: increasing σ can increase or decrease p depending on other parameters. Also, larger σ typically means slower convergence to an equilibrium.
• Small and/or slow changes in parameters (which, for example, can be brought by some policy interventions) can cause a quick and dramatic change in the population. Similar effects may be caused by stochastic forces. A prerequisite for dramatic changes is the existence of simultaneously stable equilibria.
• Changes in individual and group behaviour can be achieved by changing material benefits and costs (e.g. b), normative values (e.g. v and κ) or by changing the expectation of what others do (e.g. their estimate of p), e.g. by providing/manipulating certain information. An ‘injection’ of certain information can shift the population to the domain of attraction of a different equilibrium.
Errors in utility evaluation
So far I have assumed that individuals made no errors in evaluating utilities. To capture possible errors, one can use the quantal response equilibrium approach, which generalizes classical Nash equilibria (Goeree et al., Reference Goeree, Holt and Palfrey2016). Other ways to describe errors are possible and have received considerable attention (Young, Reference Young1998). The advantage of the quantal response equilibrium is that in this approach error probabilities depend on error costs. Figure S11 in the SI shows that decreasing precision causes the disappearance of equilibria with relatively small domains of existence and attraction and shifts the remaining solution branch towards 0.5 as individuals tend to make their decision more randomly. Overall, errors in decision-making, which are largely unavoidable in most realistic situations, can have a significant impact on the structure of equilibria by shifting p towards intermediate values.
Effects of population mixing
Stable maintenance of social norms in groups and communities can be endangered by the influx of individuals who do not share the corresponding normative values. Let m be a proportion of individuals in the whole population for whom v = k = 0, so that they are motivated only by material factors. Let F be the c.d.f. of v in the remaining part of the population and p be the frequency of individuals following the norm among in that part. Then the observed frequency of the normative behaviour in the whole population is (1 − m)p. The dynamics of p are described by the equation
Figure 2 shows that norms are relatively stable to a small infusion of newcomers but the frequency of norm followers p can be significantly reduced if m is sufficiently large.

Figure 2. Equilibrium values of frequency p in the model of population mixing (equation 3). Green, red and black diamonds correspond to three different values of the immigration rate: m = 0.2, 0.1, and 0, respectively. Filled diamonds are stable equilibria. Open diamonds are unstable equilibria separating the two stable ones. b = 1.
Effects of persuasive interventions
Certain norms stably maintained in groups and societies seriously endanger the well-being of individuals (e.g. footbinding, female genital cutting or excessive drinking in college students; see below). There is a significant effort to develop different interventions aiming to eliminate such norms. The model considered in the previous section can also be interpreted as describing a situation when a random proportion m of people have their normative values reset to zero as a result of some kind of a persuasive intervention. Figure S2 then shows that such interventions can be effective. Rather than being applied to a random sample of individuals, some intervention practices can target certain subsets of individuals. For example, persuading individuals least committed to the norm (i.e. with the smallest normative values) to permanently abandon the norm is probably the easiest. On the other hand, targeting individuals most committed to the norm (i.e. with the highest normative values) may potentially have the largest effect. In terms of our model, a successful intervention transforms the original distribution of v into a distribution truncated on one side or another (see the SI). Figure S12 in the SI illustrates the resulting effects on equilibrium values of p when the intervention targets a proportion m of individuals with the highest values of v. The effects are significant although, of course, persuading such individuals who are highly committed to the norm to abandon it is most difficult. In contrast, Figure S13 in the SI shows that targeting ‘low-hanging fruit’ individuals (i.e. with the smallest v) has no significant effect. Similar conclusions were reached in a recent paper by Efferson et al. (Reference Efferson, Vogt and Fehr2020) who used a model of conformity.
Other costs and benefits
My approach can be generalized to other costs and benefits. For example, individuals can not only suffer (passive) disapproval from others when violating the norm but also enjoy (passive) approval from those who follow the norm (e.g. if particular acts are perceived as being associated with an identity group the individuals identity with, e.g. Pryor et al., Reference Pryor, Perfors and Howe2019). This can be captured by adding an extra term to the utility of following the norm so that it becomes u 1 = v + vap, where va is the maximum normative values of (passive) approval. The only effect of this modification is that the threshold normative value for compliance becomes v* = b− (κ + va)p. Individuals are often motivated by a general desire to conform with the majority (Cialdini & Goldstein, Reference Cialdini and Goldstein2004; Pryor et al., Reference Pryor, Perfors and Howe2019). A simple way to model this is to add a normative value vc(1 − p) to u 0 and vcp to u 1, respectively, where vc is a parameter measuring the strength of conformity. This change will result in a compliance threshold v* = b + vc − (κ + 2vc)p. One can also allow for the material benefit of abandoning the norm to be frequency-dependent. For example, in the case of the footbinding norm (see below), not binding girls’ feet brings health benefits but can also result in reduced mating opportunities. One can capture this effect by subtracting terms cf p and cf (1 p) terms from utilities u 0 and u 1, respectively, where cf is the corresponding cost parameter. With this modification, v* = b + cf (κ + 2cf)p. Naturally all these additional costs and benefits can be present simultaneously which would modify v* accordingly.
Variation in other characteristics
The approach can be used if individuals differ not in a normative value v they assign to following the norm but in some other characteristics. For example, if individuals differ in how sensitive they are to (normative) cost of disapproval κ which has a c.d.f. F (z) in the population, then there is a threshold value for compliance κ* = (b − v)/p and the recurrence equation for p becomes p′ = 1 − F ((b − v)/p). Figure S14 in the SI gives an example of the corresponding bifurcation diagrams.
Both passive and active disapproval of norm violators
So far I have assumed that norm violators experienced only passive disapproval. Now assume that after making a decision about complying (i.e. choosing x = 1) or not (i.e. choosing x = 0) with the norm, individuals can also actively disapprove (or punish) norm violators, e.g. by verbally admonishing them (or just rolling their eyes or raising eyebrows). [Here, the difference between passive and active disapproval is that the latter is costly to the individuals expressing it.] The injunctive norm now is to both follow the prescribed behaviour and actively disapprove of norm violators; its normative value is denoted v as above. Let variable y = 0 and y = 1 specify the act of disapproval and let q be the frequency of individuals doing it. Then the utility of complying with the norm (i.e. choosing x = 1) is u 1 = v + as before while that of violating it is b − v− − κp − cq, where c is the maximum cost of being ‘actively’ disapproved (socially punished). Then, assuming complete knowledge of parameters, an individual chooses x = 1 if their normative value v ≡ v + + v− > v*, where
If v < v*, the individual violates the norm.
Let p′' be the frequency of individuals who have followed the norm. To define the utility of active disapproval/punishment, we assume that only norm-compliant types (i.e. individuals with x = 1) can punish and that individuals who do not punish receive only passive disapproval from those who do. Let δ be the maximum cost of punishing which could be due to a punishment act itself or potential retaliation. Assume that individuals not punishing defectors suffer a normative cost κ owing to implicit disapproval by active punishers. Under these assumptions, the utility of punishing is v − (1 − p′)δ, where the term 1 − p′ can be viewed as the ‘need for enforcement’ (Centola et al., Reference Centola, Willer and Macy2005). (Indeed, it makes no sense to pay the cost and disapprove something that does not happen, i.e. if p′ = 1.) The utility of not punishing is κq. Then a norm-complying individual will chose y = 1, if their v > v**, where
Assume as before that the normative value v has a distribution in the population with c.d.f. F (z). Then the dynamics of p and q are described by a couple of recurrence equations
Note that individuals with v > max(v*, v**) will both follow the norm and punish norm violators.
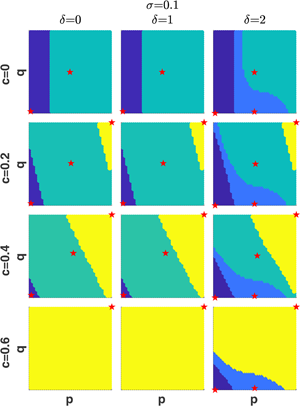
Relative to the simpler model considered above, this model has one additional dynamic variable, q, and two new parameters: the cost of active disapproval/punishment c and the cost of actively disapproving/punishing others δ. Figure 3 illustrates the effects of these new parameters on the equilibrium frequency p. Figure S15 in the SI shows the corresponding equilibrium values of q. In both of these figures the top left graph shows the stable equilibrium values when active disapproval is absent. (Note that in contrast to Figures 1 and S11 which depict both stable and unstable equilibria, here I only show stable equilibria.) Figure 3 shows that allowing for active disapproval (i.e. increasing c from zero) leads to the appearance of stable equilibria with high norm compliance even if punishment is costly (i.e. δ > 0). There can be up to two new equilibria. Punishment can have asymmetric effects on the stability of equilibria affecting the sizes of their domain of attraction. The frequency of punishers q follows p closely if p is large. That is, most contributors also punish norm-violators. If, however, punishment if costly (i.e. δ is large), only a subset of contributors with high normative values v will punish, so that q will be smaller than p. Figure S15 in the SI shows that equilibrium values of q are close to those of p except when the cost of punishment δ is high. With δ = 2, punishment happens with a lower frequency (and q* is significantly smaller than p*).

Figure 3. Stable equilibria in the model with both passive and active disapproval of norm violators with σ as the bifurcation parameter for different values of the maximum cost of being punished c and the cost of punishing others δ. v̅ = 0.8, κ = 0.2. Lognormal distribution of v.
Although Figures 3 and S15 capture the effects of σ in great detail, they cannot convey information about the domains of attraction of different equilibria. The latter are illustrated in Figure 4 for the model in which the distribution of v is bimodal. This figure shows that there can be between one and four simultaneously stable equilibria. The existence of simultaneously stable equilibria implies strong dependence on the initial conditions. Interestingly, there are situations when simultaneously stable equilibria differ in the extent of both norm compliance and punishment.

Figure 4. Stable equilibria (marked by red stars) and their domains of attractions (painted by the same color) on the (p, q)-phase plane in the model with both passive and active disapproval for different values of parameters c, δ and σ. The underlying distribution of v is a sum of two lognormal distributions with mean values at v̅ and 1 − v̅ andthe same σ. v̅ = 0.2, κ = 0.8.
All conclusions from the models with only passive disapproval remain valid in models with active disapproval (punishment). Punishment brings additional effects. In particular:
• The complexity of resulting dynamics is greatly increased. This concerns the number of equilibrium states and the extent of behavioural differences between them, e.g. in norm compliance or the level of punishment. These results imply a possibility of even greater variation between different groups and cultures (Gelfand et al., Reference Gelfand, Raver, Nishii, Leslie, Lun, Lim and Yamaguchi2011).
• Punishment stabilizes cooperative equilibria (as noticed earlier by Boyd & Richerson, Reference Boyd and Richerson1992).
• Costly punishment is largely administered by individuals with high norm internalization.
Similarly to the discussion above, it is straightforward to add additional costs and benefits to our modelling framework. For example, punishers of norm violators may expect to receive passive approval from other punishers. Alternatively, individuals who oppose the norm can actively punish norm followers. Capturing these effects in the model will modify the meaning of parameters but not the resulting dynamics.
Applications
Here I discuss how my theoretical framework can be used to better understand the effects of different policies and strategies (both successful and not) used to change social norms.
Footbinding
The painful and dangerous practice of footbinding impaired most Chinese women for a thousand years and then ended, for the most part, in a single generation as a result of the campaign of the anti-footbinding reformers. The campaign to abandon this norm had three components (Mackie, Reference Mackie1996).
The first component was a persuasive effort which explained that the rest of the world did not bind women's feet and that China was ridiculed and losing respect in the world. The second component was an educational effort explaining the health benefits of natural feet and the costs of bound feet. The third was the establishment of natural-foot societies, whose members pledged not to bind their daughters’ feet nor to let their sons marry women with bound feet. The influence mechanism here was commitment and consistency. Once people have publicly committed to something, they are more likely to follow through than if they have not.
In terms of my modelling framework, there is a material benefit, b, to abandoning footbinding (i.e. improved health), but individuals have internalized the norm (i.e. assign a positive value v to it) and expect to be subject to public disapproval leading to both normative, κ, and material, c, costs of violating the norm. The latter are due to reduced mating opportunities for daughters. The ‘actors’ here are the parents or relatives of girls enforcing the corresponding actions. One can interpret the three components of the anti-footbinding campaign in the following way. The first component introduced a normative cost of footbinding (effectively increasing the benefit b of abandoning it). The second component directly increased the perceived material benefit b of abandoning footbinding. The third component decreased the costs κ and c of disapproval by people who still abide by the norm as well as added material costs of following the norm (by decreasing the corresponding mating opportunities). These changes in perceived costs and benefits led to a fast reduction in the frequency p of footbinding.
Female genital cutting
The practice of female genital cutting found in Africa, Asia and the Middle East results in significant physical and emotional risks for tens of millions of girls and women (Berg et al., Reference Berg, Underland, Odgaard-Jensen, Fretheim and Vist2014), especially in low- and middle-income countries (Kandala et al., Reference Kandala, Ezejimofor, Uthman and Komba2018). In an attempt to change this norm, a specific policy was adopted by national and international agencies. Along with other activities, the policy called for development workers to assemble in a short period of time a group of cutting families in a community willing to abandon cutting and to declare publicly that they had done so (Efferson et al., Reference Efferson, Vogt, Elhadi, Ahmed and Fehr2015). The policy was based on a game theory model which treated norm compliance as a coordination problem (Mackie & LeJeune, Reference Mackie and LeJeune2009) and the belief that the pressure for social conformity dominated all other possible effects. The model then predicted that, once a certain critical frequency of declaring families was exceeded, the remaining families who cut would realize that abandoning the norm was in their interests and would do so. As a result, the norm would disappear completely.
In terms of my model, there are material benefits b of abandoning cutting as well as normative cost κ (owing to disapproval) and material cost c (owing to reduced mating opportunities) of abandoning the norms. The overall effects of these costs are frequency-dependent. The public declaration by non-cutting families would then effectively decrease the perceived frequency p of families following the norm. However, because of the expected heterogeneity among families in the normative benefits and costs one should not expect that p will go to zero. Rather the most likely outcome will be that p will just shift and stabilize at some intermediate value. In fact, the analysis of the frequency of cutting across 45 communities in Sudan shows that cutting rates vary continuously between 0 and 1 rather than having a discontinuous distribution with peaks at 0 and 1 as predicted by the social coordination model (Efferson et al., Reference Efferson, Vogt, Elhadi, Ahmed and Fehr2015). Efferson et al. (Reference Efferson, Vogt, Elhadi, Ahmed and Fehr2015) argued that convincing families who already have low values of cutting to make a public declaration will probably not have a large effect on remaining families. Efferson et al. (Reference Efferson, Vogt, Elhadi, Ahmed and Fehr2015) conjectured that the effort of the development workers may be more effective if it focuses on the families least receptive to the idea of abandoning cutting.
In a recent follow-up paper, Efferson et al. (Reference Efferson, Vogt and Fehr2020) used the Shelling–Granovetter model to make these arguments stronger. In their model of conformity, families differ in their sensitivity to social pressure to maintain cutting; the social pressure declines with the proportion of families who have already abandoned it. Efferson et al. (Reference Efferson, Vogt and Fehr2020) assumed that a persuasive intervention makes families abandon cutting completely. They compared three different intervention strategies focusing on individuals most amenable to change or most resistant to change, or on a random sample from the population. They concluded that although interventions often target samples of the population most amenable to change, targeting a representative random sample is a more robust way to reduce cutting. My results reported in the section on ‘Persuasive interventions’ above back the validity of these conclusions in a more general framework. Overall, my results support earlier conclusions of Efferson et al. (Reference Efferson, Vogt, Elhadi, Ahmed and Fehr2015, Reference Efferson, Vogt and Fehr2020) that understanding heterogeneity in a population is essential for predicting the effects of interventions. As I argue here, evaluating the expected effectiveness of different campaigns requires information on the distribution of values and beliefs in the target population. (See figure S3 in Efferson et al. (Reference Efferson, Vogt, Elhadi, Ahmed and Fehr2015) for an empirical example of such a distribution.)
College students’ drinking
Heavy alcohol consumption and binge drinking is a serious problem in many colleges. Data show that drinking rates increase significantly during the transition from high school to college (Labrie et al., Reference Labrie, Lamb and Pedersen2009). A contributing factor to this increase is that students typically overestimate the frequency and amount that other students drink. As a result, many students are often under a strong social pressure to drink in excess of what they would prefer (Park et al., Reference Park, Klein, Smith and Martel2009).
There are three main methods of social norm interventions focusing on correcting misperceptions about risky behaviours and social norms (Miller and Prentice, Reference Miller and Prentice2016). Social norms marketing is the dissemination of a single factual message documenting the (high) incidence of some desirable behaviour. Personalized normative feedback is the information about themselves as well as their peers. Focus group discussions aim to achieve similar goals by capitalizing on a readily available reference group. Considerable research indicates that feedback on close referents has the strongest effect on behaviour, making the personalized normative feedback and focus group discussions more powerful. All three methods have been used in efforts to reduce students’ drinking.
In terms of my models, these methods aim to provide correct (or desirable) information about variable p. If p is lower than the students thought, it may also force them to increase their estimate of benefit b of abandoning the norm. (The logic is that if many others do not do it, there may be indeed high benefits of reduced drinking.) The information about discrepancies between individual behaviour and the average behaviour in their reference group may force the subjects to reduce their estimates of the level of social disapproval κq they expect to receive from peers. The most receptive individuals to change will be those who are drinking more than they want to because of a desire to be socially accepted. Information that p is low may also increase the likelihood that students who oppose heavy drinking will actively disapprove/punish back norm followers (i.e heavy drinkers). Moreover, manipulating identity cues may force individuals to reevaluate the normative value v of a particular behaviour. Observers usually interpret behaviours as freely chosen and reflecting the actor's private preferences and dispositions (Gilbert & Malone, Reference Gilbert and Malone1995). That is, high frequency p of drinking may be interpreted as evidence of high normative values v assigned to it. Correcting this misinterpretation can reduce drinking. Some interventions also attempt to change the perceived benefits of behaviour, e.g. by reports of how uncomfortable students feel with their drinking practices.
Pro-environmental behaviour
Social norms have a significant impact on a range of pro-environmental behaviours (Miller & Prentice, Reference Miller and Prentice2016; Farrow et al., Reference Farrow, Grolleau and Ibanez2017; Nyborg, Reference Nyborg2018; Jachimowicz et al., Reference Jachimowicz, Hauser, O'Brien, Sherman and Galinsky2018). Methods used to change human behaviour affecting the environment are similar to those mentioned above (e.g. social marketing, personalized normative feedback and focus group discussions). Proenvironmental behaviour is a kind of a public good. As stressed by Miller and Prentice (Reference Miller and Prentice2016), in the case of public goods, ‘perceived norms tend to be unclear or absent, rather than biased, and thus the interventions work primarily by making people more aware of their own behaviour and where it falls in the distribution’ (p. 348). For example, feedback in environmental interventions can focus on how people's weekly kilowatt use compares with that of their neighbours. Risky behaviour interventions are most effective when they utilize social identity considerations (e.g. same-gender friends, teammates, sorority sisters). In contrast, public-goods interventions invoke comparisons with the group with whom the focal individual shares public goods, e.g. nearby residents.
Two types of information have proved most useful when providing such feedback: (a) how common particular environmental behaviours are among group members (descriptive norms); and (b) the degree of approval of these behaviours by group members (injunctive norms). Informing people that their neighbours use less energy will convey to people that energy use reduction is possible. In terms of our models, this can make them reduce the perceived material cost/benefit ratio and simultaneously increase normative value v of pro-environmental behaviour. Informing people about the degree of neighbours’ approval (e.g. Jachimowicz et al., Reference Jachimowicz, Hauser, O'Brien, Sherman and Galinsky2018) accomplishes several things. It sends a better signal of their true intentions so that the focal individual will not feel like a sucker. This will decrease the normative costs of pro-environmental behaviour. [Note that in the model, the psychological cost of being a sucker is frequency dependent and can be described in a similar way to that of reduced mating opportunity for the footbinding and genital cutting norms discussed above.] It can also signal expected approval by others, characterized by parameter va in the model. Providing the information about neighbours’ preferences can also exploit existing preferences for conformity and the sense of belonging to the community measured by parameter vc. Energy consumption by high users is reduced the most if the corresponding information is presented publicly rather privately (Delmas & Lessem, Reference Delmas and Lessem2014). This implies that people have normative concerns about their social standing and reputation. This effect can be captured by adjusting the normative value v of the behaviour.
Discussion
Understanding human decision-making in social situations requires one to consider not only material costs and benefits involved, but also conformity, beliefs and internalized values, and expected (dis)approval and punishment by others for norm violation. Predicting changes in social behaviours, e.g. following certain social interventions, requires mathematical models capturing these factors. In a recent review of theories of social norms and pro-environmental behaviour, Farrow et al. (Reference Farrow, Grolleau and Ibanez2017) observed that ‘there is no unified theoretical framework regarding how norms operate in the decision-making process’ (p. 6) and then concluded that ‘developing a single theory regarding the effect of social norms on choice may indeed be unrealistic’ (p. 10). Contrary to this view, here I suggest a possible unifying theoretical approach. My approach is mathematically simple, yet general and is able to capture various costs and benefits, both material and normative, associated with different norm-related actions and behaviours, including punishment and disapproval by others. The approach also captures errors in the decision-making process. Moreover, it explicitly accounts for differences between individuals in their values, sensitivity to the actions of others, and in beliefs about the population state. My models make predictions about the dynamics of the frequencies of different behaviours given certain initial conditions.
Although injunctive social norms are universally viewed as one of the most important factors in human social life, modelling work on their dynamics is rather limited. My models, which are based on an integration of two earlier unrelated theoretical approaches (i.e. the Schelling–Granovetter model and Gavrilets and Richerson model), aim to extend it. Various earlier applications of the Schelling–Granovetter model (e.g. Neary & Newton Reference Neary and Newton2017; Efferson et al., Reference Efferson, Vogt and Fehr2020) have followed the original formulation and operated in terms of general conformity ‘thresholds’ (defined as a minimum frequency of a particular behaviour in the population needed for a focal individual to adopt the same behaviour). In contrast, instead of Granovetter's ‘thresholds’, I used variables and parameters common in social psychology and cultural evolution, including those describing the effects of social (dis)approval, punishment for norm violations and norm internalization. I identified equilibria (both homogeneous and heterogeneous) and studied their dependence on meaningful parameters. I explicitly showed that there can be multiple equilibria, and studied their domains of attraction and the time to convergence to equilibria. I showed that the shape of the distribution of normative values strongly affects the resulting dynamics. I demonstrated how immigration of individuals with different values changes population behaviour and did a similar analysis of persuasive interventions. At the end I went beyond the Schelling–Granovetter model by introducing an additional ‘action’ that individuals can take – punishment of norm violators. I then repeated most of my analysis for a new two-dimensional model. I showed that punishment greatly increases the complexity of the resulting dynamics, stabilizes cooperative equilibria, and promotes increased norm diversity between groups and cultures.
To illustrate possible applications of my approach I considered strategies that have been developed by practitioners to abolish the norms of footbinding and female genital cutting, to decrease college students’ drinking and to increase pro-environmental behaviours. The approach can also be applied to other norms including seat-belt usage, (Miller & Prentice, Reference Miller and Prentice2016), behaviour in online interactions (Matias, Reference Matias2019), hostility towards a different ethnic group (Bauer et al., Reference Bauer, Cahlíkovác, Chytilová and Zelinský2018), littering in public places (Cialdini et al., Reference Cialdini, Reno and Kallgren1990) and breach of professional norms (Hechter, Reference Hechter2008). My models provide a way to mathematically explore the effects of possible interventions. My results show that the development of better policies can be informed by measuring the distributions of norms, values and beliefs in the population. These can be estimated using experimental manipulations (e.g. Kimbrough and Vostroknutov, Reference Kimbrough and Vostroknutov2016) or surveys. There are different surveys in the literature touching on different components of the model. For example, expected net material effects of following or abandoning a norm (related to the parameter b) were estimated in Chen et al. (Reference Chen, Xu and Day2017) in a study of pro-environmental behaviour. Efferson et al. (Reference Efferson, Vogt, Elhadi, Ahmed and Fehr2015) used implicit association tests to estimate the distribution of individual values associated with a norm of genital cutting in a population (see their Fig. S3). Jachimowicz et al. (Reference Jachimowicz, Hauser, O'Brien, Sherman and Galinsky2018) measured second-order beliefs, that is, beliefs of subjects about their neighbours’ beliefs about the importance of energy conservation (related to the parameter κ of the model). Hong et al. (Reference Hong, Chen, Wang and Xu2020) measured various personality traits including tendencies for general conformity (related to the parameter vc of the model) in a set of subjects within the context of energy conservation. Using model (S3a) in the SI, the relationship between the probability P that an individual follows the norm and their different characteristics can be written as log p/(1-p)=λΔu where the difference in utilities Δu is a linear function of parameters. Therefore, given appropriate survey data one can estimate the relevant parameters of the model using standard methods of logistic regression and then make predictions about the target group behaviour or effects of different policies. The main challenge in applying the models would be to measure a number of different parameters/characteristics in the same system. Although this is not easy, without such a step predicting the outcomes of interventions is hardly possible. Note that theoretical results show that quick and large changes in the population can only happen under certain conditions (specifically, when the underlying dynamics have multiple equilibria).
The definition of injunctive social norms used here implies that, in a sense, a social norm exists as long as people believe it exists. The latter observation makes some social norms an example of Merton's (Reference Merton1948) concept of the self-fulfilling prophecy, which in turn stems from Thomas’ (Reference Thomas1928) postulate that ‘If men define situations as real, they are real in their consequences’. [A classic example of a self-fulfilling prophecy is a bank run started by customers withdrawing money because they heard a rumour about the bank's insolvency. Another example is provided by the Greek myth of Oedipus.] It should be clear that what is really important for human behaviour is not the actual values costs and benefits (b, v, κ, etc.) but what people believe they are. This points to the importance of changing human beliefs via interventions if the goal is changing their behaviours. The modelling approach above can be used to study the dynamics of self-fulfilling (and self-defeating) prophecies. It can also be used to develop a scientific evolutionary perspective on the dynamics of human moral beliefs (Boehm, Reference Boehm2012) and the effects of culture on human behaviour (Richerson et al., Reference Richerson, Baldini, Bell, Demps, Frost, Hillis and Zefferman2016).
Here I have followed Cialdini et al. (Reference Cialdini, Reno and Kallgren1990) in distinguishing between descriptive norms (which specify the perception of what is commonly done) and injunctive norms (which specify the perception of what is commonly approved/sanctioned). This approach has been further developed by Bicchieri (Reference Bicchieri2006) and Bicchieri and Muldoon (Reference Bicchieri, Muldoon and Zalta2014), who characterize these norms according to social expectations. In Bicchieri's approach, descriptive norms are understood as individuals’ empirical expectations about others’ behaviour while injunctive norms are viewed as individuals’ normative expectations about others’ behaviour. An important factor in her approach is the extent of social dependence of individuals’ preferences for engaging in relevant behaviours: some preferences are socially interdependent while others are socially independent. This allows one to differentiate, within Cialdini's descriptive norms, ‘customs’ (such as washing your hands before eating a meal) from ‘descriptive norms’ (e.g. driving on the right side of the road). Both are empirically expected but the former entail socially independent preferences while the latter entail socially dependent preferences. Then, within Cialdini's injunctive norms, one can also tell apart ‘moral rules’ (e.g. do not cheat) from ‘social norms’ (e.g. energy saving). Both are normatively expected but the former entail socially independent preferences while the latter entail socially dependent preferences. (I am grateful to an anonymous reviewer who pointed out these distinctions.)
My approach for defining the utility function effectively (a) postulates that it depends on both immediate and future costs and benefits (both material and normative) and (b) implies that individuals are able to predict the reaction of their groupmates to their own action. Viewed this way, my approach can be interpreted as an example of application of a recently introduced strategy revision protocol called foresight (Perry et al., Reference Perry, Shrestha Duwal, Vose and Gavrilets2018; Perry & Gavrilets, Reference Perry and Gavrilets2020; Gavrilets, Reference Gavrilets, Gelfand, Chiu and Hong2021)). Foresight aims to capture in game theoretic models the ability of humans and some non-human animals to foresee the future (Szpunar et al., Reference Szpunar, Spreng and Schactera2014) and make intertemporal choices (Frederick et al., Reference Frederick, Loewenstein and O'Donoghue2002) as well as their ‘theory of mind’, i.e. the ability to reason about the knowledge and thought processes of others in the social context (Premack & Wodruff, Reference Premack and Wodruff1979; Krupenye et al., Reference Krupenye, Kano, Hirata, Call and Tomasello2016; de Waal, Reference de Waal2016). Our earlier work has shown that foresight can solve the first- and second-order free-rider problems in the presence of punishment (Perry et al., Reference Perry, Shrestha Duwal, Vose and Gavrilets2018; Perry & Gavrilets, Reference Perry and Gavrilets2020), can lead to the evolution of social institutions by the route of self-interested design (Gavrilets & Shrestha, Reference Gavrilets and Duwal Shrestha2020) or undermine cooperation via tactical deception (Gavrilets, Reference Gavrilets, Gelfand, Chiu and Hong2021)). The models and behaviours studied here provide an additional illustration of the power of foresight.
I followed earlier work postulating that people have the ability to internalize social norms. This ability could have evolved because it allows individuals to reduce the costs associated with information gathering, processing and decision making and the costs of monitoring, punishment and conditional rewards that would otherwise be necessary to ensure cooperation (Henrich & Ensminger, Reference Henrich, Ensminger, Ensminger and Henrich2014). It could also increase individual survival via its effects on the capacity to maintain connections with a social safety net. Gavrilets and Richerson (Reference Gavrilets and Richerson2017) have formalized these arguments in a mathematical model. Norm internalization can also allow individuals and groups to adjust their utility functions in situations with a rapidly changing environment when genetic mechanisms would be too slow to react (Gintis, Reference Gintis2003). An important question is which norms become injunctive, i.e. get internalized. Kimbrough and Vostroknutov (Reference Kimbrough and Vostroknutov2019) proposed (and provided a supporting mathematical model) that these are behaviours that minimize the aggregated dissatisfaction of all group members. It would be interesting to study this question using an evolutionary dynamics approach.
My results provide further evidence for the importance of accounting for intrinsic differences between individuals in game-theoretic models. Within-group heterogeneity in various characteristics is not only ubiquitous in real groups but it can greatly affect the resulting evolutionary dynamics (Young, Reference Young1993; Khan & Peters, Reference Khan and Peters2014; Gavrilets & Fortunato, Reference Gavrilets and Fortunato2014; Gavrilets, Reference Gavrilets2015; Gavrilets & Richerson, Reference Gavrilets and Richerson2017; Neary & Newton, Reference Neary and Newton2017; Hilbe et al., Reference Hilbe, Schmid, Tkadlec, Chatterjee and Nowak2018; Radzvilavicius et al., Reference Radzvilavicius, Stewart and Plotkin2019; Hauser et al., Reference Hauser, Hilbe, Chatterjee and Nowak2019; Efferson et al., Reference Efferson, Vogt and Fehr2020). My results show that not only summary statistics, like the mean and variance, but also the shape of the underlying distribution can play an important role. Estimating within group heterogeneity is necessary for predicting group behaviour.
Some of my models allowed for active disapproval (social punishment) of norm violators. There are multiple reasons for why people punish. One is that punishment of norm violators is internalized, is viewed as the right thing to do, and brings moral satisfaction (retributive approach; Carlsmith, Reference Carlsmith2008; Cushman, Reference Cushman2015). Another is that punishment may bring material benefits immediately by restoring whatever was lost or it can deter future misdeeds by the norm violator or observers (consequentialist approach; Cushman, Reference Cushman2015). People can also punish because of general conformity (if others punish, so should I) or adherence to the fairness norm (if others pay costs of punishment, so should I). These factors lead to conditional punishment based on expectation that others will punish as well (Kamei, Reference Kamei2018; Molleman et al., Reference Molleman, Kölle, Starmer and Gächter2019). There is also ‘false enforcement’ (Centola et al., Reference Centola, Willer and Macy2005) when people enforce unpopular norms to show that they have complied out of genuine conviction and not because of social pressure. People can also punish to remove the competitive advantage of the cheater (Gavrilets, Reference Gavrilets2012; Raihani & Bshary, Reference Raihani and Bshary2019) or exhibit antisocial punishment, e.g. just out of spite or to achieve a competitive advantage over others (Raihani & Bshary, Reference Raihani and Bshary2019). Raihani and Bshary (Reference Raihani and Bshary2019) stress the role of competitive punishment which is clearly important within the context of experimental economic games when subjects are motivated by monetary rewards and the desire to do better than their peers. In real-life situations meant to be described by the models studied above, a norm violation by an individual does not result in negative material consequences for others, and winning a competition with others is not a part of individual decision making. Rather in my models punishing others is a result of norm internalization, conformity and (potentially) errors.
There are a number of directions in which my approach can be extended. Rather than assuming that individuals obtain information about the state of their group as a whole, one can assume that they observe only the behaviour of their social contacts in a large social network. One can further assume that some of the contacts are more important than others introducing opinion leaders or role models (Henrich & Gil-White, Reference Henrich and Gil-White2001). One then can study how changing the behaviours and communications of the most visible and influential members of a group or community affects the group dynamics. People can also differ in whose social approval they value. This will translate into differences in their motivation to comply with the norm. Spatial structure of populations can also affect these processes. One can introduce uncertainties in individuals’ estimate of the state of their group and update their knowledge via Bayesian learning. In the models considered above, norm violation by an individual did not cause any material losses to others. One can study the effects of introducing such losses as would happen, for example, with queue jumping behaviour (Milgram et al., Reference Milgram, Liberty, Toledo and Wackenhut1986). On a more technical side, one can attempt to evaluate or approximate the corresponding integrals in two-dimensional models analytically. This might lead to more transparent and intuitive results. So far I have treated individual normative values as constant. Modelling how they evolve as individuals to adjust their preferences as a result of learning, conformity or changes in social identity will be an important next step. Also important is to consider a model extension with two competing ‘norms’ so that punishment/disapproval can go both ways. This would require an increase in the dimensionality of the model from two to three.
Social norms, values and beliefs are critically important for all aspects of our social life from the way we address each other, dress and position ourselves in an elevator to norms of conduct in family, class room, business meeting or politics, to their effects on human behaviour in violent conflicts. This is how it has been during all of our history (and most definitely in pre-historic human groups and societies). This remains true in modern societies characterized by increased connectedness and the massive flow of information often causing rapid changes in norms. Investigating the origins, maintenance and effects of social norms demands not only observational and experimental data, but also solid theoretical foundations. The latter require the building of corresponding mathematical models and testing of their predictions. Having all of these components in place will allow us not only to better understand historical and current social processes but also to develop practical policies that would make our societies better.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/ehs.2020.58
Acknowledgements
I thank A. Bentley, C. Efferson, M. Lapinski-LaFaive, P. J. Richerson, G. Shteynberg, D. Tverskoi and reviewers for comments and suggestions.
Author contributions
SG designed and performed the research and wrote the paper.
Financial support
This work was supported by the US Army Research Office grants W911NF-14-1-0637 and W911NF-18-1-0138 and the Office of Naval Research grant W911NF-17-1-0150, the National Institute for Mathematical and Biological Synthesis through NSF Award no. EF-0830858, and by the University of Tennessee, Knoxville.
Research transparency and reproducibility
All data are in the manuscript. The Matlab code used is available upon request.