Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cheng, Chuangxun
2013.
Multiplicity one of regular Serre weights.
Israel Journal of Mathematics,
Vol. 198,
Issue. 1,
p.
419.
Rozensztajn, Sandra
2015.
Potentially semi-stable deformation rings for discrete series extended types.
Journal de l’École polytechnique — Mathématiques,
Vol. 2,
Issue. ,
p.
179.
GEE, TOBY
LIU, TONG
and
SAVITT, DAVID
2015.
THE WEIGHT PART OF SERRE’S CONJECTURE FOR .
Forum of Mathematics, Pi,
Vol. 3,
Issue. ,
Paškūnas, Vytautas
2015.
On the Breuil–Mézard conjecture.
Duke Mathematical Journal,
Vol. 164,
Issue. 2,
Allen, Patrick B.
2016.
Deformations of polarized automorphic Galois representations and adjoint Selmer groups.
Duke Mathematical Journal,
Vol. 165,
Issue. 13,
Sander, Fabian
2016.
A local proof of the Breuil–Mézard conjecture in the scalar semi‐simplification case.
Journal of the London Mathematical Society,
Vol. 94,
Issue. 2,
p.
447.
Paškūnas, Vytautas
2016.
On 2-dimensional 2-adic Galois representations of local and global fields.
Algebra & Number Theory,
Vol. 10,
Issue. 6,
p.
1301.
DEMBÉLÉ, LASSINA
DIAMOND, FRED
and
ROBERTS, DAVID P.
2016.
SERRE WEIGHTS AND WILD RAMIFICATION IN TWO-DIMENSIONAL GALOIS REPRESENTATIONS.
Forum of Mathematics, Sigma,
Vol. 4,
Issue. ,
Hellmann, Eugen
and
Schraen, Benjamin
2016.
Density of potentially crystalline representations of fixed weight.
Compositio Mathematica,
Vol. 152,
Issue. 8,
p.
1609.
LUDWIG, JUDITH
2017.
A QUOTIENT OF THE LUBIN–TATE TOWER.
Forum of Mathematics, Sigma,
Vol. 5,
Issue. ,
Park, Chol
2017.
Reduction modulo 𝑝 of certain semi-stable representations.
Transactions of the American Mathematical Society,
Vol. 369,
Issue. 8,
p.
5425.
Morra, Stefano
and
Park, Chol
2017.
Serre weights for three-dimensional ordinary Galois representations.
Journal of the London Mathematical Society,
Vol. 96,
Issue. 2,
p.
394.
Shotton, Jack
2018.
The Breuil–Mézard conjecture when l≠p.
Duke Mathematical Journal,
Vol. 167,
Issue. 4,
Le, Daniel
Morra, Stefano
and
Park, Chol
2018.
On mod p local-global compatibility for GL3(Qp) in the non-ordinary case.
Proceedings of the London Mathematical Society,
Vol. 117,
Issue. 4,
p.
790.
Le, Daniel
Le Hung, Bao V.
Levin, Brandon
and
Morra, Stefano
2018.
Potentially crystalline deformation rings and Serre weight conjectures: shapes and shadows.
Inventiones mathematicae,
Vol. 212,
Issue. 1,
p.
1.
Caraiani, Ana
Emerton, Matthew
Gee, Toby
Geraghty, David
Paškūnas, Vytautas
and
Shin, Sug Woo
2018.
Patching and the -adic Langlands program for .
Compositio Mathematica,
Vol. 154,
Issue. 3,
p.
503.
Guerberoff, Lucio
and
Park, Chol
2019.
Semistable deformation rings in even
Hodge–Tate weights.
Pacific Journal of Mathematics,
Vol. 298,
Issue. 2,
p.
299.
Le, Daniel
Le Hung, Bao V.
and
Levin, Brandon
2019.
Weight elimination in Serre-type conjectures.
Duke Mathematical Journal,
Vol. 168,
Issue. 13,
Hu, Yongquan
and
Paškūnas, Vytautas
2019.
On crystabelline deformation rings of $$\mathrm {Gal}(\overline{\mathbb {Q}}_p/\mathbb {Q}_p)$$ Gal ( Q ¯ p / Q p ) (with an appendix by Jack Shotton).
Mathematische Annalen,
Vol. 373,
Issue. 1-2,
p.
421.
Bellovin, Rebecca
and
Gee, Toby
2019.
G-valued local deformation rings and global
lifts.
Algebra & Number Theory,
Vol. 13,
Issue. 2,
p.
333.
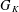 $G_{K}$,
$G_{K}$, 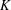 $K$ a finite extension of
$K$ a finite extension of 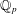 $\mathbb{Q}_{p}$, for any
$\mathbb{Q}_{p}$, for any 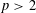 $p>2$ (up to the question of determining precise values
for the multiplicities that occur). In the case that
$p>2$ (up to the question of determining precise values
for the multiplicities that occur). In the case that 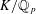 $K/\mathbb{Q}_{p}$ is unramified, we also determine most of the
multiplicities. We then apply these results to the weight part of Serre’s
conjecture, proving a variety of results including the
Buzzard–Diamond–Jarvis conjecture.
$K/\mathbb{Q}_{p}$ is unramified, we also determine most of the
multiplicities. We then apply these results to the weight part of Serre’s
conjecture, proving a variety of results including the
Buzzard–Diamond–Jarvis conjecture.




