Hostname: page-component-77c89778f8-5wvtr Total loading time: 0 Render date: 2024-07-22T03:17:12.453Z Has data issue: false hasContentIssue false
  • English
  • Français

ENUMERATION OF MEANDERS AND MASUR–VEECH VOLUMES

Part of: Deformations of analytic structures Riemann surfaces Graph theory Low-dimensional topology

Published online by Cambridge University Press:  23 March 2020

VINCENT DELECROIX ,
ÉLISE GOUJARD ,
PETER ZOGRAF  and
ANTON ZORICH
VINCENT DELECROIX
Affiliation:
Laboratoire Bordelais de Recherche en Informatique, 33405Talence, France; vincent.delecroix@u-bordeaux.fr
ÉLISE GOUJARD
Affiliation:
Institut de Mathématiques de Bordeaux, 33405Talence, France; elise.goujard@gmail.com
PETER ZOGRAF
Affiliation:
Steklov Math. Institute and Chebyshev Laboratory, St. Petersburg199178, Russia; zograf@pdmi.ras.ru
ANTON ZORICH
Affiliation:
Center for Advanced Studies, Skoltech, Institut Mathématique de Jussieu, 75205 Paris, France; anton.zorich@gmail.com

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A meander is a topological configuration of a line and a simple closed curve in the plane (or a pair of simple closed curves on the 2-sphere) intersecting transversally. Meanders can be traced back to H. Poincaré and naturally appear in various areas of mathematics, theoretical physics and computational biology (in particular, they provide a model of polymer folding). Enumeration of meanders is an important open problem. The number of meanders with 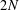$2N$ crossings grows exponentially when 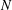$N$ grows, but the long-standing problem on the precise asymptotics is still out of reach.

We show that the situation becomes more tractable if one additionally fixes the topological type (or the total number of minimal arcs) of a meander. Then we are able to derive simple asymptotic formulas for the numbers of meanders as 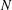$N$ tends to infinity. We also compute the asymptotic probability of getting a simple closed curve on a sphere by identifying the endpoints of two arc systems (one on each of the two hemispheres) along the common equator.

The new tools we bring to bear are based on interpretation of meanders as square-tiled surfaces with one horizontal and one vertical cylinder. The proofs combine recent results on Masur–Veech volumes of moduli spaces of meromorphic quadratic differentials in genus zero with our new observation that horizontal and vertical separatrix diagrams of integer quadratic differentials are asymptotically uncorrelated. The additional combinatorial constraints we impose in this article yield explicit polynomial asymptotics.

MSC classification

Primary: 32G15: Moduli of Riemann surfaces, Teichmüller theory
Secondary: 57M50: Geometric structures on low-dimensional manifolds 30F30: Differentials on Riemann surfaces 05C30: Enumeration in graph theory
Type
Topology
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e4
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - SA
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© The Author(s) 2020

References

Andersen, J. E., Chekhov, L. O., Penner, R. C., Reidys, C. M. and Sułkowski, P., ‘Topological recursion for chord diagrams, RNA complexes, and cells in moduli spaces’, Nuclear Phys. B 866(3) (2013), 414–443.CrossRefGoogle Scholar
Arnold, V. I., ‘Ramified covering ℂP2 → S 4 , hyperbolicity and projective topology’, Sib. Math. J. 29(5) (1988), 36–47.Google Scholar
Athreya, J., Eskin, A. and Zorich, A., ‘Counting generalized Jenkins–Strebel differentials’, Geom. Dedicata 170(1) (2014), 195–217.CrossRefGoogle Scholar
Athreya, J., Eskin, A. and Zorich, A., ‘Right-angled billiards and volumes of moduli spaces of quadratic differentials on ℂP1’, Ann. Sci. Éc. Norm. Supér. (4) 49 (2016), 1307–1381.Google Scholar
Delecroix, V., Goujard, E., Zograf, P. and Zorich, A., ‘Contribution of one-cylinder square-tiled surfaces to Masur-Veech volumes’, Astérisque 415(1) (2020), with an Appendix by P. Engel, to appear.Google Scholar
Delecroix, V., Goujard, E., Zograf, P. and Zorich, A., ‘Square-tiled surfaces with fixed combinatorics in invariant arithmetic suborbifolds: density, equidistribution, non-correlation’, in preparation.Google Scholar
Delecroix, V., Goujard, E., Zograf, P. and Zorich, A., ‘Masur-Veech volumes, frequencies of simple closed geodesics and intersection numbers of moduli spaces of curves’, Preprint, 2019, arXiv:1908.08611.Google Scholar
Di Francesco, P., Golinelli, O. and Guitter, E., ‘Meander, folding, and arch statistics’, Math. Comput. Model. 26(8–10) (1997), 97–147.CrossRefGoogle Scholar
Di Francesco, P., Golinelli, O. and Guitter, E., ‘Meanders: exact asymptotics’, Nuclear Phys. B 570(3) (2000), 699–712.CrossRefGoogle Scholar
Douady, A. and Hubbard, J., ‘On the density of Strebel differentials’, Invent. Math. 30(2) (1975), 175–179.CrossRefGoogle Scholar
El-Baz, D., Huang, B. and Lee, M., ‘Effective equidistribution of primitive rational points on expanding horospheres’, Preprint, 2018, arXiv:1811.04019.Google Scholar
Eskin, A. and Mirzakhani, M., ‘Invariant and stationary measures for the SL2(ℝ) action on moduli space’, Publ. Inst. Hautes Etudes Sci. 127 (2018), 95–324.CrossRefGoogle Scholar
Eskin, A., Mirzakhani, M. and Mohammadi, A., ‘Isolation, equidistribution, and orbit closures for the SL2(ℝ)-action on moduli space’, Ann. of Math. (2) 182(2) (2015), 673–721.CrossRefGoogle Scholar
Eskin, A., Mirzakhani, M. and Mohammadi, A., ‘Effective counting of simple closed geodesics on hyperbolic surfaces’, Preprint 2019, arXiv:1905.04435.Google Scholar
Eskin, A. and Okounkov, A., ‘Pillowcases and quasimodular forms’, inAlgebraic Geometry and Number Theory, Honor of Vladimir Drinfeld’s 50th Birthday, (ed. Victor, G.) Progress in Mathematics, 253 (Birkhäuser, Basel, 2006), 1–25.Google Scholar
Goujard, E., ‘Siegel–Veech constants for strata of moduli spaces of quadratic differentials’, GAFA 25(5) (2015), 1440–1492.Google Scholar
Goujard, E., ‘Volumes of strata of moduli spaces of quadratic differentials: getting explicit values’, Ann. Inst. Fourier (Grenoble) 66(6) (2016), 2203–2251.CrossRefGoogle Scholar
Gould, H. W., ‘Combinatorial identities. A standardized set of tables listing 500 binomial coefficient summations’ Rev. ed. (English) Morgantown (1972).Google Scholar
Jensen, I., ‘A transfer matrix approach to the enumeration of plane meanders’, J. Phys. A 33(34) (2000), 5953–5963.CrossRefGoogle Scholar
Kontsevich, M. and Zorich, A., ‘Connected components of the moduli spaces of Abelian differentials with prescribed singularities’, Invent. Math. 153(3) (2003), 631–678.CrossRefGoogle Scholar
Lando, S. K. and Zvonkin, A. K., ‘Plane and projective meanders’, Theoret. Comput. Sci. 117 (1993), 227–241.CrossRefGoogle Scholar
Lanneau, E., Nguyen, D.-M. and Wright, A., ‘Finiteness of Teichmüller curves in non-arithmetic rank 1 orbit closures’, Amer. J. Math. 139(6) (2017), 1449–1463.CrossRefGoogle Scholar
Masur, H., ‘Interval exchange transformations and measured foliations’, Ann. of Math. (2) 115 (1982), 169–200.CrossRefGoogle Scholar
Mirzakhani, M., ‘Growth of the number of simple closed geodesics on hyperbolic surfaces’, Ann. of Math. (2) 168(1) (2008), 97–125.CrossRefGoogle Scholar
Mirzakhani, M. and Wright, A., ‘The boundary of an affine invariant submanifold’, Invent. Math. 209(3) (2017), 927–984.CrossRefGoogle Scholar
Moon, J. W., Counting Labelled Trees, Canadian Mathematical Monographs, 1 (Canadian Mathematical Congress, Montreal, 1970), 113.Google Scholar
Nevo, A., Rühr, R. and Weiss, B., ‘Effective counting on translation surfaces’, Adv. Math. 360 (2020), 106890.CrossRefGoogle Scholar
Poincaré, H., ‘Sur un téorème de géométrie’, Rend. Circ. Mat. Palermo (2) 33 (1912), 375–407. (Oeuvres, T.VI, 499–538).CrossRefGoogle Scholar
Strebel, K., Quadratic Differentials, Ergebnisse der Mathematik und ihrer Grenzgebiete (Springer, Berlin, 1984), 184.CrossRefGoogle Scholar
Veech, W., ‘Gauss measures for transformations on the space of interval exchange maps’, Ann. of Math. (2) 115 (1982), 201–242.CrossRefGoogle Scholar
Wright, A., ‘The field of definition of affine invariant submanifolds of the moduli space of Abelian differentials’, Geom. Topol. 18(3) (2014), 1323–1341.CrossRefGoogle Scholar
Wright, A., ‘Cylinder deformations in orbit closures of translation surfaces’, Geom. Topol. 19(1) (2015), 413–438.CrossRefGoogle Scholar
Zimmer, R. J., Ergodic Theory and Semisimple Groups, Monographs in Mathematics, 81 (Birkhäuser, Boston–Basel–Stuttgart, 1984), 209.CrossRefGoogle Scholar
Zorich, A., ‘Flat surfaces’, inFrontiers in Number Theory, Physics, and Geometry. I (Springer, Berlin, 2006), 437–583.CrossRefGoogle Scholar
Zorich, A., ‘Square-tiled surfaces and Teichmüller volumes of the moduli spaces of Abelian differentials’, inRigidity in Dynamics and Geometry (Springer, Berlin, 2002), 459–471, (Cambridge, 2000).CrossRefGoogle Scholar
Zorich, A., ‘Explicit Jenkins–Strebel representatives of all strata of Abelian and quadratic differentials’, J. Mod. Dyn. 2(1) (2008), 139–185.CrossRefGoogle Scholar