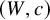1. Introduction
1.1. Polypositroids
The aim of this work is to study a new class of polytopes, which we call polypositroids. These are polytopes which are simultaneously generalized permutohedra (or polymatroids) and alcoved polytopes.
A permutohedron is the convex hull of the orbit of a point in
![]() $\mathbb {R}^n$
under the action of the symmetric group
$\mathbb {R}^n$
under the action of the symmetric group
![]() $S_n$
. A generalized permutohedron is obtained from a permutohedron by parallel translation of some of the facets. The class of generalized permutohedra include many classical polytopes: the usual permutohedron, the associahedron, hypersimplices, matroid polytopes, and many others. Generalized permutohedra are polytopal analogues of matroids, and are essentially equivalent to the polymatroids of Edmonds and the closely related submodular functions [Reference EdmondsEdm, Reference PostnikovPo09, Reference Castillo and LiuCL].
$S_n$
. A generalized permutohedron is obtained from a permutohedron by parallel translation of some of the facets. The class of generalized permutohedra include many classical polytopes: the usual permutohedron, the associahedron, hypersimplices, matroid polytopes, and many others. Generalized permutohedra are polytopal analogues of matroids, and are essentially equivalent to the polymatroids of Edmonds and the closely related submodular functions [Reference EdmondsEdm, Reference PostnikovPo09, Reference Castillo and LiuCL].
An alcoved polytope is a polytope whose facets are normal to roots in the type
![]() $A_{n-1}$
root system. In [Reference Lam and PostnikovLP07], we studied the class of integer alcoved polytopes, which are (convex) unions of alcoves in the affine Coxeter arrangement of type A. In the present paper, we work with alcoved polytopes that may not be integral.
$A_{n-1}$
root system. In [Reference Lam and PostnikovLP07], we studied the class of integer alcoved polytopes, which are (convex) unions of alcoves in the affine Coxeter arrangement of type A. In the present paper, we work with alcoved polytopes that may not be integral.
Our initial motivation for studying polypositroids as a subclass of polymatroids comes from the theory of total positivity. Lusztig [Reference LusztigLus] and Postnikov [Reference PostnikovPo06] have defined the totally nonnegative Grassmannian
![]() $\mathrm {Gr}(k,n)_{\geq 0}$
, a subspace of the real Grassmannian
$\mathrm {Gr}(k,n)_{\geq 0}$
, a subspace of the real Grassmannian
![]() $\mathrm {Gr}(k,n)$
of k-planes in
$\mathrm {Gr}(k,n)$
of k-planes in
![]() $\mathbb {R}^n$
. Any point
$\mathbb {R}^n$
. Any point
![]() $X \in \mathrm {Gr}(k,n)$
gives rise to a (realizable) matroid
$X \in \mathrm {Gr}(k,n)$
gives rise to a (realizable) matroid
![]() $M_X$
. When
$M_X$
. When
![]() $X \in \mathrm {Gr}(k,n)_{\geq 0}$
is totally nonnegative, the matroid
$X \in \mathrm {Gr}(k,n)_{\geq 0}$
is totally nonnegative, the matroid
![]() $M_X$
is called a positroid, short for “positive matroid.” Positroids were classified in [Reference PostnikovPo06] and [Reference OhOh], and the geometry of positroid varieties in the Grassmannian was studied by Knutson-Lam-Speyer [Reference Knutson, Lam and SpeyerKLS].
$M_X$
is called a positroid, short for “positive matroid.” Positroids were classified in [Reference PostnikovPo06] and [Reference OhOh], and the geometry of positroid varieties in the Grassmannian was studied by Knutson-Lam-Speyer [Reference Knutson, Lam and SpeyerKLS].
To a matroid M on the set
![]() $\{1,2,\ldots ,n\}$
, one has an associated matroid polytope
$\{1,2,\ldots ,n\}$
, one has an associated matroid polytope
![]() $P_M \subset \mathbb {R}^n$
. Our investigations began with the observation that a matroid M is a positroid if and only if
$P_M \subset \mathbb {R}^n$
. Our investigations began with the observation that a matroid M is a positroid if and only if
![]() $P_M$
is an alcoved polytope (Theorem 2.1). Polypositroids are thus “positive polymatroids.” In the present work, we study polypositroids from a discrete geometer’s perspective, leaving aside potential connections to Grassmannians, and so on.
$P_M$
is an alcoved polytope (Theorem 2.1). Polypositroids are thus “positive polymatroids.” In the present work, we study polypositroids from a discrete geometer’s perspective, leaving aside potential connections to Grassmannians, and so on.
Whereas matroids are notoriously difficult to parametrize, the subclass of positroids were parametrized in [Reference PostnikovPo06, Reference OhOh]. In Theorem 6.12, we give a parametrization of polypositroids, showing that they are in bijection with Coxeter necklaces and with balanced graphs. Coxeter necklaces and balanced graphs are generalizations of the Grassmann necklaces and decorated permutations of [Reference PostnikovPo06]. The set of generalized permutohedra attains a cone structure under the Minkowski sum, and the corresponding cone is the cone of submodular functions
![]() ${\mathcal {C}}_{\mathrm {sub}}$
[Reference EdmondsEdm]. Alcoved polytopes and polypositroids also form cones
${\mathcal {C}}_{\mathrm {sub}}$
[Reference EdmondsEdm]. Alcoved polytopes and polypositroids also form cones
![]() ${\mathcal {C}}_{\mathrm {alc}}$
and
${\mathcal {C}}_{\mathrm {alc}}$
and
![]() ${\mathcal {C}}_{\mathrm { pol}}$
. There is a (projection) map of cones
${\mathcal {C}}_{\mathrm { pol}}$
. There is a (projection) map of cones
![]() ${\mathcal {C}}_{\mathrm {sub}} \to {\mathcal {C}}_{\mathrm {alc}}$
, and we show in Theorem 4.8 that the image of this map is
${\mathcal {C}}_{\mathrm {sub}} \to {\mathcal {C}}_{\mathrm {alc}}$
, and we show in Theorem 4.8 that the image of this map is
![]() ${\mathcal {C}}_{\mathrm {pol}}$
. In Corollary 6.14 and Theorem 4.9, we describe the extremal rays and give defining inequalities for the cone
${\mathcal {C}}_{\mathrm {pol}}$
. In Corollary 6.14 and Theorem 4.9, we describe the extremal rays and give defining inequalities for the cone
![]() ${\mathcal {C}}_{\mathrm {pol}}$
. For example, the extremal rays of
${\mathcal {C}}_{\mathrm {pol}}$
. For example, the extremal rays of
![]() ${\mathcal {C}}_{\mathrm {pol}}$
are indexed by directed cycles on
${\mathcal {C}}_{\mathrm {pol}}$
are indexed by directed cycles on
![]() $\{1,2,\ldots ,n\}$
.
$\{1,2,\ldots ,n\}$
.
The normal fan of the permutohedron is the braid fan associated to the arrangement of hyperplanes
![]() $\{x_i-x_j =0\}$
. Generalized permutohedra are exactly the polytopes with a normal fan, a coarsening of the braid fan. In Section 8, we study the possible normal fans
$\{x_i-x_j =0\}$
. Generalized permutohedra are exactly the polytopes with a normal fan, a coarsening of the braid fan. In Section 8, we study the possible normal fans
![]() ${\mathcal {N}}(P)$
for a generic simple polypositroid P. In contrast to generalized permutohedra, there is more than one such normal fan, and each such
${\mathcal {N}}(P)$
for a generic simple polypositroid P. In contrast to generalized permutohedra, there is more than one such normal fan, and each such
![]() ${\mathcal {N}}(P)$
is a coarsening of the braid fan.
${\mathcal {N}}(P)$
is a coarsening of the braid fan.
We show in Lemma 8.2 that each maximal cone
![]() $C_T$
of
$C_T$
of
![]() ${\mathcal {N}}(P)$
is labeled by an alternating noncrossing tree. The maximal cones
${\mathcal {N}}(P)$
is labeled by an alternating noncrossing tree. The maximal cones
![]() $C_w$
,
$C_w$
,
![]() $w \in S_n$
satisfying
$w \in S_n$
satisfying
![]() $C_w \subset C_T$
are described in Proposition 8.22 in terms of a dual noncrossing circular-alternating tree. In Theorem 8.4, we show that the normal fan
$C_w \subset C_T$
are described in Proposition 8.22 in terms of a dual noncrossing circular-alternating tree. In Theorem 8.4, we show that the normal fan
![]() ${\mathcal {N}}(P)$
is characterized by a matching ensemble, a collection of perfect matchings, one for each bipartite subgraph of the complete graph, satisfying certain axioms. Our matching ensembles are a variant of the matching ensembles of Oh and Yoo [Reference Oh and YooOY], and the matching fields of Sturmfels and Zelevinsky [Reference Sturmfels and ZelevinskySZ]. In Theorem 8.1, we show that all generic simple polypositroids have the same f-vector, identical to that of the cyclohedron.
${\mathcal {N}}(P)$
is characterized by a matching ensemble, a collection of perfect matchings, one for each bipartite subgraph of the complete graph, satisfying certain axioms. Our matching ensembles are a variant of the matching ensembles of Oh and Yoo [Reference Oh and YooOY], and the matching fields of Sturmfels and Zelevinsky [Reference Sturmfels and ZelevinskySZ]. In Theorem 8.1, we show that all generic simple polypositroids have the same f-vector, identical to that of the cyclohedron.
1.2. Coxeter polypositroids
In the second part of this work, we generalize the theory of polypositroids to the root-system theoretic setting. Let V be a real vector space,
![]() $R \subset V$
be a crystallographic root system with Weyl group W, and
$R \subset V$
be a crystallographic root system with Weyl group W, and
![]() $R^+ \subset R$
be a choice of positive roots. A generalized W-permutohedron is a polytope
$R^+ \subset R$
be a choice of positive roots. A generalized W-permutohedron is a polytope
![]() $P \subset V$
whose edges are in the directions of R.
$P \subset V$
whose edges are in the directions of R.
Now fix the choice of a Coxeter element c. Define the twisted root system
![]() ${\tilde R}:= (I-c)^{-1} R$
. We define a
${\tilde R}:= (I-c)^{-1} R$
. We define a
![]() $(W,c)$
-twisted alcoved polytope to be a polytope
$(W,c)$
-twisted alcoved polytope to be a polytope
![]() $P \subset V$
whose facet normals belong to the twisted roots
$P \subset V$
whose facet normals belong to the twisted roots
![]() ${\tilde R}$
. These polytopes are c-twisted variants of the alcoved polytopes we studied in [Reference Lam, Postnikov, Kac and PopovLP18]. A
${\tilde R}$
. These polytopes are c-twisted variants of the alcoved polytopes we studied in [Reference Lam, Postnikov, Kac and PopovLP18]. A
![]() $(W,c)$
-polypositroid is a polytope that is simultaneously a generalized W-permutohedron and a
$(W,c)$
-polypositroid is a polytope that is simultaneously a generalized W-permutohedron and a
![]() $(W,c)$
-twisted alcoved polytope. When R is of type
$(W,c)$
-twisted alcoved polytope. When R is of type
![]() $A_{n-1}$
and c is the long cycle
$A_{n-1}$
and c is the long cycle
![]() $(12 \cdots n)$
, this definition reduces to the earlier one.
$(12 \cdots n)$
, this definition reduces to the earlier one.
In general, the class of
![]() $(W,c)$
-polypositroids cannot be parametrized in the same manner that we did for polypositroids. We introduce a larger class of
$(W,c)$
-polypositroids cannot be parametrized in the same manner that we did for polypositroids. We introduce a larger class of
![]() $(W,c)$
-prepolypositroids as a compromise. The set of
$(W,c)$
-prepolypositroids as a compromise. The set of
![]() $(W,c)$
-prepolypositroids is defined as a cone, by giving the facet inequalities (16.1) satisfied by the support function. We define
$(W,c)$
-prepolypositroids is defined as a cone, by giving the facet inequalities (16.1) satisfied by the support function. We define
![]() $(W,R^+,c)$
-Coxeter necklaces and
$(W,R^+,c)$
-Coxeter necklaces and
![]() $(W,c)$
-balanced arrays and show in Theorem 16.5 that these objects are in bijection with
$(W,c)$
-balanced arrays and show in Theorem 16.5 that these objects are in bijection with
![]() $(W,c)$
-prepolypositroids. We also show that there is a projection map from the cone
$(W,c)$
-prepolypositroids. We also show that there is a projection map from the cone
![]() ${\mathcal {C}}_{\mathrm {sub}}^W$
of W-submodular functions (see [Reference Ardila, Castillo, Eur and PostnikovACEP]) to the cone
${\mathcal {C}}_{\mathrm {sub}}^W$
of W-submodular functions (see [Reference Ardila, Castillo, Eur and PostnikovACEP]) to the cone
![]() ${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
of
${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
of
![]() $(W,c)$
-prepolypositroids, and we conjecture (Conjecture 17.2) that this map is surjective.
$(W,c)$
-prepolypositroids, and we conjecture (Conjecture 17.2) that this map is surjective.
In Section 18, we connect the theory of
![]() $(W,c)$
-prepolypositroids to cluster algebras. Let
$(W,c)$
-prepolypositroids to cluster algebras. Let
![]() ${\mathcal {A}}(W,R^+,c)$
be the cluster algebra of finite type associated to the Coxeter element c, as studied by Yang and Zelevinsky [Reference Yang and ZelevinskyYZ]. We show, using the work of Padrol et al. [Reference Padrol, Palu, Pilaud and PlamondonP4], in Theorem 18.5 that each exchange relation of
${\mathcal {A}}(W,R^+,c)$
be the cluster algebra of finite type associated to the Coxeter element c, as studied by Yang and Zelevinsky [Reference Yang and ZelevinskyYZ]. We show, using the work of Padrol et al. [Reference Padrol, Palu, Pilaud and PlamondonP4], in Theorem 18.5 that each exchange relation of
![]() ${\mathcal {A}}(W,R^+,c)$
gives rise to an inequality satisfied by the cone
${\mathcal {A}}(W,R^+,c)$
gives rise to an inequality satisfied by the cone
![]() ${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
of
${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
of
![]() $(W,c)$
-prepolypositroids. We show that
$(W,c)$
-prepolypositroids. We show that
![]() $(W,c)$
-prepolypositroids are closely related to generalized associahedra, one of our main examples of
$(W,c)$
-prepolypositroids are closely related to generalized associahedra, one of our main examples of
![]() $(W,c)$
-polypositroids.
$(W,c)$
-polypositroids.
In Section 19, with the aim of studying the normal fans of
![]() $(W,c)$
-prepolypositroids, we develop notions of alternating and c-noncrossing for root systems, and a notion of c-noncrossing tree. These notions are related to the theory of finite type cluster algebras, and to the theory of reflection factorizations of Coxeter elements.
$(W,c)$
-prepolypositroids, we develop notions of alternating and c-noncrossing for root systems, and a notion of c-noncrossing tree. These notions are related to the theory of finite type cluster algebras, and to the theory of reflection factorizations of Coxeter elements.
1.3. Membranes
The third part of the paper is devoted to membranes. In Section 20, we define R-membranes, for a root system
![]() $R\subset V$
, which are essentially triangulated 2-dimensional surfaces in V homeomorphic to wedges of disks, such that every edge of every triangle in them is a parallel translation of a root from R. An R-membrane is minimal if it has minimal possible surface area among all membranes with the same boundary loop. We view the problem of describing minimal membranes as a discrete version of Plateau’s problem from geometric measure theory concerning the existence of a minimal surface with a given boundary. In the rest of the paper, we discuss membranes of type A. In Section 21, we show that membranes of type A are closely related to Postnikov’s plabic graphs, introduced in the study of the totally nonnegative Grassmannian
$R\subset V$
, which are essentially triangulated 2-dimensional surfaces in V homeomorphic to wedges of disks, such that every edge of every triangle in them is a parallel translation of a root from R. An R-membrane is minimal if it has minimal possible surface area among all membranes with the same boundary loop. We view the problem of describing minimal membranes as a discrete version of Plateau’s problem from geometric measure theory concerning the existence of a minimal surface with a given boundary. In the rest of the paper, we discuss membranes of type A. In Section 21, we show that membranes of type A are closely related to Postnikov’s plabic graphs, introduced in the study of the totally nonnegative Grassmannian
![]() $\mathrm {Gr}(k,n)_{\geq 0}$
[Reference PostnikovPo06]. For each positroid, there is a class of reduced plabic graphs connected with each other by local moves. Each reduced plabic graph gives a parametrization of the associated positroid cell in
$\mathrm {Gr}(k,n)_{\geq 0}$
[Reference PostnikovPo06]. For each positroid, there is a class of reduced plabic graphs connected with each other by local moves. Each reduced plabic graph gives a parametrization of the associated positroid cell in
![]() $\mathrm {Gr}(k,n)_{\geq 0}$
.
$\mathrm {Gr}(k,n)_{\geq 0}$
.
Membranes (of type A) are in bijection with plabic graphs with faces labelled by integer vectors. In Section 22, we show that local moves of plabic graphs correspond to octahedron and tetrahedron moves of membranes. In Section 23, we show that minimal membranes correspond to reduced plabic graphs.
In Sections 24, 25, and 26, we discuss special classes of membranes associated with positroids and polypositroids. In Section 27, we define semisimple membranes as membranes that project bijectively onto the Coxeter plane. We show that notions of semisimple membranes and minimal membranes are equivalent to each other (for a particular class of boundary loops).
The structures that we study in this paper are related to the theory of cluster algebras in several different ways. While in Section 18, we connect
![]() $(W,c)$
-prepolypositroids to cluster algebras of finite type, in Section 28, we connect membranes (of type A) to a certain class of cluster algebras, which, in general, are not of finite type. We discuss the higher octahedron recurrence as a certain rational recurrence relation on variables
$(W,c)$
-prepolypositroids to cluster algebras of finite type, in Section 28, we connect membranes (of type A) to a certain class of cluster algebras, which, in general, are not of finite type. We discuss the higher octahedron recurrence as a certain rational recurrence relation on variables
![]() $x_{\lambda }$
labelled by integer vectors
$x_{\lambda }$
labelled by integer vectors
![]() $\lambda $
. This relation naturally extends the octahedron recurrence on
$\lambda $
. This relation naturally extends the octahedron recurrence on
![]() $\mathbb {Z}^3$
[Reference SpeyerSpe] to a higher dimensional integer lattice. With each polypositroid P, we associate a cluster algebra
$\mathbb {Z}^3$
[Reference SpeyerSpe] to a higher dimensional integer lattice. With each polypositroid P, we associate a cluster algebra
![]() ${\mathcal {A}}_P$
generated by some finite subset of variables
${\mathcal {A}}_P$
generated by some finite subset of variables
![]() $x_{\lambda }$
. Minimal membranes for the polypositroid P correspond to a class of clusters of this cluster algebra, and local moves of membranes correspond to cluster mutations. Remarkably, the class of cluster algebras
$x_{\lambda }$
. Minimal membranes for the polypositroid P correspond to a class of clusters of this cluster algebra, and local moves of membranes correspond to cluster mutations. Remarkably, the class of cluster algebras
![]() ${\mathcal {A}}_P$
is the same as the subclass associated to positroids, which Galashin and Lam have shown [Reference Galashin and LamGL] to be isomorphic to the coordinate rings of open positroid varieties [Reference Knutson, Lam and SpeyerKLS].
${\mathcal {A}}_P$
is the same as the subclass associated to positroids, which Galashin and Lam have shown [Reference Galashin and LamGL] to be isomorphic to the coordinate rings of open positroid varieties [Reference Knutson, Lam and SpeyerKLS].
Finally, in Section 29, we propose an area of study, which we dub the “Asymptotic Cluster Algebra.” We pose a problem related to asymptotics of membranes under dilations. The setup of membranes extends several models from statistical physics.
Part I Polypositroids
Throughout the paper, we use the following notation. Let
![]() $[n]:=\{1,2,\ldots ,n\}$
. Let
$[n]:=\{1,2,\ldots ,n\}$
. Let
![]() $\binom {[n]}{k}$
denote the set of k-element subsets of
$\binom {[n]}{k}$
denote the set of k-element subsets of
![]() $[n]$
. Also, let
$[n]$
. Also, let
![]() $e_1,\dots ,e_n$
denote the standard basis of
$e_1,\dots ,e_n$
denote the standard basis of
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
2. Positroid polytopes
The material of this section serves as motivation, and is largely independent of the rest of the work.
Let
![]() $\mathrm {Gr}(k,n)$
denote the Grassmannian of k-planes in
$\mathrm {Gr}(k,n)$
denote the Grassmannian of k-planes in
![]() $\mathbb {R}^n$
. We may represent a point
$\mathbb {R}^n$
. We may represent a point
![]() $X \in \mathrm {Gr}(k,n)$
as a
$X \in \mathrm {Gr}(k,n)$
as a
![]() $k \times n$
matrix. For a k-element subset
$k \times n$
matrix. For a k-element subset
![]() $I\in \binom {[n]}{k}$
, the Plücker coordinate
$I\in \binom {[n]}{k}$
, the Plücker coordinate
![]() $\Delta _I(X)$
is defined to be the
$\Delta _I(X)$
is defined to be the
![]() $k \times k$
minor indexed by the columns I. The matroid
$k \times k$
minor indexed by the columns I. The matroid
![]() ${\mathcal {M}}_X$
is given by
${\mathcal {M}}_X$
is given by
![]() ${\mathcal {M}}_X:= \{I \in \binom {[n]}{k} \mid \Delta _I(X) \neq 0\}$
. The totally nonnegative Grassmannian [Reference PostnikovPo06]
${\mathcal {M}}_X:= \{I \in \binom {[n]}{k} \mid \Delta _I(X) \neq 0\}$
. The totally nonnegative Grassmannian [Reference PostnikovPo06]
![]() $\mathrm {Gr}(k,n)_{\geq 0}$
is the subspace of
$\mathrm {Gr}(k,n)_{\geq 0}$
is the subspace of
![]() $\mathrm {Gr}(k,n)$
represented by matrices, all of whose Plücker coordinates are nonnegative. The matroid of a totally nonnegative point
$\mathrm {Gr}(k,n)$
represented by matrices, all of whose Plücker coordinates are nonnegative. The matroid of a totally nonnegative point
![]() $X \in \mathrm {Gr}(k,n)_{\geq 0}$
is called a positroid.
$X \in \mathrm {Gr}(k,n)_{\geq 0}$
is called a positroid.
The matroid polytope
![]() $P_{\mathcal {M}}$
of a matroid
$P_{\mathcal {M}}$
of a matroid
![]() ${\mathcal {M}}$
is the convex hull of the vectors
${\mathcal {M}}$
is the convex hull of the vectors
![]() $e_I$
,
$e_I$
,
![]() $I \in {\mathcal {M}}$
, where
$I \in {\mathcal {M}}$
, where
![]() $e_I:=e_{i_1} + \cdots + e_{i_k} \in \mathbb {R}^n$
if
$e_I:=e_{i_1} + \cdots + e_{i_k} \in \mathbb {R}^n$
if
![]() $I = \{i_1,\ldots ,i_k\}$
. By [Reference Gelfand, Goresky, Macpherson and SerganovaG2MS], matroid polytopes are exactly those polytopes whose vertices belong to
$I = \{i_1,\ldots ,i_k\}$
. By [Reference Gelfand, Goresky, Macpherson and SerganovaG2MS], matroid polytopes are exactly those polytopes whose vertices belong to
![]() $\{e_I \mid I \in \binom {[n]}{k}\}$
and whose edges are parallel to vectors of the form
$\{e_I \mid I \in \binom {[n]}{k}\}$
and whose edges are parallel to vectors of the form
![]() $e_i - e_j$
. We have the following characterization of the matroid polytopes of positroids.
$e_i - e_j$
. We have the following characterization of the matroid polytopes of positroids.
Theorem 2.1. A matroid
![]() ${\mathcal {M}}$
is a positroid if and only if the matroid polytope
${\mathcal {M}}$
is a positroid if and only if the matroid polytope
![]() $P_{\mathcal {M}}$
is an alcoved polytope, that is, it is given by inequalities of the form
$P_{\mathcal {M}}$
is an alcoved polytope, that is, it is given by inequalities of the form
![]() $c_{ij} \leq x_i + x_{i+1} + \cdots + x_j \leq b_{ij}$
, for
$c_{ij} \leq x_i + x_{i+1} + \cdots + x_j \leq b_{ij}$
, for
![]() $1 \leq i < j \leq n$
, where
$1 \leq i < j \leq n$
, where
![]() $c_{ij}, b_{ij} \in \mathbb {R}$
.
$c_{ij}, b_{ij} \in \mathbb {R}$
.
We discovered Theorem 2.1 over a decade ago, and it has since found a number of applications, for example, to positively oriented matroids [Reference Ardila, Rincón and WilliamsARW17] (see [Reference Arkani-Hamed, Lam and SpradlinALS, Reference EarlyEar, Reference Lukowski, Parisi and WilliamsLPW] for other appearances of positroid polytopes).
To prove Theorem 2.1, we use a classification of positroids due to Oh [Reference OhOh] (see also [Reference LamLam, Section 8.2]). The Bruhat partial order on
![]() $\binom {[n]}{k}$
is defined as follows. For two subsets
$\binom {[n]}{k}$
is defined as follows. For two subsets
![]() $I, J \in \binom {[n]}{k}$
, we write
$I, J \in \binom {[n]}{k}$
, we write
![]() $I \leq J$
if
$I \leq J$
if
![]() $I = \{i_1 < i_2 <\cdots < i_k\}$
,
$I = \{i_1 < i_2 <\cdots < i_k\}$
,
![]() $J = \{j_1 < j_2 < \cdots < j_k\}$
, and we have
$J = \{j_1 < j_2 < \cdots < j_k\}$
, and we have
![]() $i_r \leq j_r$
for
$i_r \leq j_r$
for
![]() $r = 1,2,\ldots ,k$
. For
$r = 1,2,\ldots ,k$
. For
![]() $I \in \binom {[n]}{k}$
, the Schubert matroid
$I \in \binom {[n]}{k}$
, the Schubert matroid
![]() ${\mathcal {S}}_I$
is defined as
${\mathcal {S}}_I$
is defined as
 $$ \begin{align*}{\mathcal{S}}_I:= \{J \in {\binom{[n]}{k}} \mid I \leq J\} \end{align*} $$
$$ \begin{align*}{\mathcal{S}}_I:= \{J \in {\binom{[n]}{k}} \mid I \leq J\} \end{align*} $$
and has minimal element I in the Bruhat order. For
![]() $a \in [n]$
, let
$a \in [n]$
, let
![]() $<_a$
denote the cyclically rotated order on
$<_a$
denote the cyclically rotated order on
![]() $[n]$
with minimum a, that is,
$[n]$
with minimum a, that is,
![]() $a<_a (a+1) <_a\cdots <_a n <_a 1 <_a\cdots <_a (a-1)$
, which induces a partial order
$a<_a (a+1) <_a\cdots <_a n <_a 1 <_a\cdots <_a (a-1)$
, which induces a partial order
![]() $\leq _a$
on
$\leq _a$
on
![]() $\binom {[n]}{k}$
. Let
$\binom {[n]}{k}$
. Let
![]() ${\mathcal {S}}_{I,a} := \{J \in \binom {[n]}{k} \mid I \leq _a J\}$
denote the cyclically rotated Schubert matroid. Equivalently,
${\mathcal {S}}_{I,a} := \{J \in \binom {[n]}{k} \mid I \leq _a J\}$
denote the cyclically rotated Schubert matroid. Equivalently,
![]() ${\mathcal {S}}_{I,a} := c^{a-1}({\mathcal {S}}_{c^{-a+1}(I)})$
, where c is the long cycle
${\mathcal {S}}_{I,a} := c^{a-1}({\mathcal {S}}_{c^{-a+1}(I)})$
, where c is the long cycle
![]() $(1,2,\dots ,n)$
in the symmetric group
$(1,2,\dots ,n)$
in the symmetric group
![]() $S_n$
naturally acting on
$S_n$
naturally acting on
![]() $[n]$
and
$[n]$
and
![]() ${[n]\choose k}$
.
${[n]\choose k}$
.
A
![]() $(k,n)$
-Grassmann necklace
$(k,n)$
-Grassmann necklace
![]() ${\mathcal {I}} = (I_1,I_2,\ldots ,I_n)$
is an n-tuple of k-element subsets of
${\mathcal {I}} = (I_1,I_2,\ldots ,I_n)$
is an n-tuple of k-element subsets of
![]() $[n]$
satisfying the following condition: for each
$[n]$
satisfying the following condition: for each
![]() $a \in [n]$
, we have
$a \in [n]$
, we have
-
1. if
 $a \notin I_a$
, then
$a \notin I_a$
, then
 $I_{a+1} = I_a$
,
$I_{a+1} = I_a$
, -
2. otherwise,
 $a \in I_a$
and
$a \in I_a$
and
 $I_{a+1} = (I_a \setminus \{a\}) \cup \{a'\}$
for some
$I_{a+1} = (I_a \setminus \{a\}) \cup \{a'\}$
for some
 $a' \in [n]$
,
$a' \in [n]$
,
with indices taken modulo n.
Theorem 2.2 [Reference OhOh, Reference PostnikovPo06]
Let
![]() ${\mathcal {I}}= (I_1,I_2,\ldots ,I_n)$
be a
${\mathcal {I}}= (I_1,I_2,\ldots ,I_n)$
be a
![]() $(k,n)$
-Grassmann necklace. Then the intersection of cyclically rotated Schubert matroids
$(k,n)$
-Grassmann necklace. Then the intersection of cyclically rotated Schubert matroids
is a positroid, and the map
![]() ${\mathcal {I}} \mapsto {\mathcal {M}}_{\mathcal {I}}$
gives a bijection between
${\mathcal {I}} \mapsto {\mathcal {M}}_{\mathcal {I}}$
gives a bijection between
![]() $(k,n)$
-Grassmann necklaces and positroids of rank k on
$(k,n)$
-Grassmann necklaces and positroids of rank k on
![]() $[n]$
.
$[n]$
.
Proof of Theorem 2.1
Let
![]() $\Delta (k,n)$
denote the hypersimplex, the convex hull of all points
$\Delta (k,n)$
denote the hypersimplex, the convex hull of all points
![]() $e_I$
, for
$e_I$
, for
![]() $I \in \binom {[n]}{k}$
. The matroid polytope
$I \in \binom {[n]}{k}$
. The matroid polytope
![]() $P_{{\mathcal {S}}_{I,a}}$
is the intersection of the hypersimplex
$P_{{\mathcal {S}}_{I,a}}$
is the intersection of the hypersimplex
![]() $\Delta (k,n)$
with the inequalities
$\Delta (k,n)$
with the inequalities
for
![]() $i = 1,2,\ldots ,n$
. In particular,
$i = 1,2,\ldots ,n$
. In particular,
![]() $P_{{\mathcal {S}}_{I,a}}$
is an alcoved polytope.
$P_{{\mathcal {S}}_{I,a}}$
is an alcoved polytope.
Let
![]() ${\mathcal {M}}$
be an arbitrary matroid. Recall, that any matroid has a unique minimal base in the Bruhat partial order
${\mathcal {M}}$
be an arbitrary matroid. Recall, that any matroid has a unique minimal base in the Bruhat partial order
![]() $\leq $
on
$\leq $
on
![]() ${[n]\choose k}$
, and thus in any cyclically rotated partial order
${[n]\choose k}$
, and thus in any cyclically rotated partial order
![]() $\leq _a$
. Denote by
$\leq _a$
. Denote by
![]() $I_a({\mathcal {M}})$
the minimal base of
$I_a({\mathcal {M}})$
the minimal base of
![]() ${\mathcal {M}}$
with respect to
${\mathcal {M}}$
with respect to
![]() $\leq _a$
. Let
$\leq _a$
. Let
![]() $Q = \mathrm {env}(P_{\mathcal {M}})$
be the alcoved envelope of
$Q = \mathrm {env}(P_{\mathcal {M}})$
be the alcoved envelope of
![]() $P_{\mathcal {M}}$
, that is, the smallest alcoved polytope that contains
$P_{\mathcal {M}}$
, that is, the smallest alcoved polytope that contains
![]() $P_{\mathcal {M}}$
. Then Q is given by the intersection of the rotated Schubert matroid polytopes
$P_{\mathcal {M}}$
. Then Q is given by the intersection of the rotated Schubert matroid polytopes
![]() $P_{{\mathcal {S}}_{I_a({\mathcal {M}}),a}}$
for
$P_{{\mathcal {S}}_{I_a({\mathcal {M}}),a}}$
for
![]() $a =1,2,\ldots ,n$
(see Lemma 5.1). It is known [Reference PostnikovPo06, Lemma 16.3] that for any matroid
$a =1,2,\ldots ,n$
(see Lemma 5.1). It is known [Reference PostnikovPo06, Lemma 16.3] that for any matroid
![]() ${\mathcal {M}}$
, the n-tuple
${\mathcal {M}}$
, the n-tuple
![]() ${\mathcal {I}}({\mathcal {M}})=(I_1({\mathcal {M}}),I_2({\mathcal {M}}),\ldots ,I_n({\mathcal {M}}))$
is a
${\mathcal {I}}({\mathcal {M}})=(I_1({\mathcal {M}}),I_2({\mathcal {M}}),\ldots ,I_n({\mathcal {M}}))$
is a
![]() $(k,n)$
-Grassmann necklace, and
$(k,n)$
-Grassmann necklace, and
![]() ${\mathcal {M}}_{\mathcal {I}}$
is called the positroid envelope of
${\mathcal {M}}_{\mathcal {I}}$
is called the positroid envelope of
![]() ${\mathcal {M}}$
[Reference Knutson, Lam and SpeyerKLS]. Thus, Q is the matroid polytope of the positroid envelope of
${\mathcal {M}}$
[Reference Knutson, Lam and SpeyerKLS]. Thus, Q is the matroid polytope of the positroid envelope of
![]() ${\mathcal {M}}$
. In particular,
${\mathcal {M}}$
. In particular,
![]() $P_{\mathcal {M}}$
is alcoved if and only if
$P_{\mathcal {M}}$
is alcoved if and only if
![]() $Q = P_{\mathcal {M}}$
if and only if
$Q = P_{\mathcal {M}}$
if and only if
![]() ${\mathcal {M}}$
is a positroid.
${\mathcal {M}}$
is a positroid.
A decorated permutation on
![]() $[n]$
is a pair
$[n]$
is a pair
![]() $\pi ^: = (\pi ,\mathrm {col})$
, where
$\pi ^: = (\pi ,\mathrm {col})$
, where
![]() $\pi $
is a permutation of
$\pi $
is a permutation of
![]() $[n]$
and
$[n]$
and
![]() $\mathrm {col}$
is an assignment of one of two colors “black” and “white” to each of the fixed points
$\mathrm {col}$
is an assignment of one of two colors “black” and “white” to each of the fixed points
![]() $\{i \in [n] \mid \pi (i) = i\}$
. We say that
$\{i \in [n] \mid \pi (i) = i\}$
. We say that
![]() $i \in [n]$
is an antiexceedance of
$i \in [n]$
is an antiexceedance of
![]() $\pi ^:$
if
$\pi ^:$
if
![]() $\pi ^{-1}(i)> i$
or
$\pi ^{-1}(i)> i$
or
![]() $\pi (i) = i$
and i is colored white. Given a
$\pi (i) = i$
and i is colored white. Given a
![]() $(k,n)$
-Grassmann necklace
$(k,n)$
-Grassmann necklace
![]() ${\mathcal {I}} = (I_1,I_2,\ldots ,I_n)$
, we define a decorated permutation
${\mathcal {I}} = (I_1,I_2,\ldots ,I_n)$
, we define a decorated permutation
![]() $\pi ^:({\mathcal {I}})$
by
$\pi ^:({\mathcal {I}})$
by
-
1. if
 $I_{a+1} = I_a - \{a\} \cup \{a'\}, a' \neq a$
, then
$I_{a+1} = I_a - \{a\} \cup \{a'\}, a' \neq a$
, then
 $\pi (a) = a'$
;
$\pi (a) = a'$
; -
2. if
 $I_{a+1} = I_a$
and
$I_{a+1} = I_a$
and
 $a \notin I_a$
, then
$a \notin I_a$
, then
 $\pi (i) =i$
and i is colored black;
$\pi (i) =i$
and i is colored black; -
3. if
 $I_{a+1} = I_a$
and
$I_{a+1} = I_a$
and
 $a \in I_a$
, then
$a \in I_a$
, then
 $\pi (i) = i$
and i is colored white.
$\pi (i) = i$
and i is colored white.
[Reference PostnikovPo06, Lemma 16.2] states that the map
![]() ${\mathcal {I}} \to \pi ^:({\mathcal {I}})$
is a bijection between
${\mathcal {I}} \to \pi ^:({\mathcal {I}})$
is a bijection between
![]() $(k,n)$
-Grassmann necklaces and decorated permutations on
$(k,n)$
-Grassmann necklaces and decorated permutations on
![]() $[n]$
with k antiexceedances.
$[n]$
with k antiexceedances.
3. Polypositroids
In this paper, we consider several classes of convex polytopes in
![]() $\mathbb {R}^n$
. All polytopes lie in an affine hyperplane
$\mathbb {R}^n$
. All polytopes lie in an affine hyperplane
![]() $H=H_k:=\{x \in \mathbb {R}^n \mid x_1 + \cdots + x_n = k\}$
, for some constant k. For the majority of this work, the reader may assume that the hyperplane H has been fixed.
$H=H_k:=\{x \in \mathbb {R}^n \mid x_1 + \cdots + x_n = k\}$
, for some constant k. For the majority of this work, the reader may assume that the hyperplane H has been fixed.
3.1. Generalized permutohedra
Definition 3.1 [Reference PostnikovPo09]
A polytope
![]() $P\subset \mathbb {R}^n$
is called a generalized permutohedron if all edges of P are parallel to a vector of the form
$P\subset \mathbb {R}^n$
is called a generalized permutohedron if all edges of P are parallel to a vector of the form
![]() $e_i-e_j$
.
$e_i-e_j$
.
The class of generalized permutohedra include many classical polytopes: the usual permutohedron, the associahedron, hypersimplices, and many others (see [Reference PostnikovPo09]). Let us give several alternative ways to describe the class of generalized permutohedra. Let
![]() $(\mathbb {R}^n)^*$
denote the vector space of linear functions on
$(\mathbb {R}^n)^*$
denote the vector space of linear functions on
![]() $\mathbb {R}^n$
. For a face F of a polytope P, the normal cone
$\mathbb {R}^n$
. For a face F of a polytope P, the normal cone
![]() $C_F \subset (\mathbb {R}^n)^*$
to F is given by
$C_F \subset (\mathbb {R}^n)^*$
to F is given by
The normal fan
![]() ${\mathcal F}_P$
is the complete fan in
${\mathcal F}_P$
is the complete fan in
![]() $(\mathbb {R}^n)^*$
consisting of all cones
$(\mathbb {R}^n)^*$
consisting of all cones
![]() $C_F$
as F varies over all the faces of P. We say that a complete fan
$C_F$
as F varies over all the faces of P. We say that a complete fan
![]() ${\mathcal F}'$
is a coarsening of a complete fan
${\mathcal F}'$
is a coarsening of a complete fan
![]() ${\mathcal F}$
if the maximal cones of
${\mathcal F}$
if the maximal cones of
![]() ${\mathcal F}'$
are unions of the maximal cones of
${\mathcal F}'$
are unions of the maximal cones of
![]() ${\mathcal F}$
.
${\mathcal F}$
.
For a permutation
![]() $w\in S_n$
, let
$w\in S_n$
, let
![]() $v_w = -(w^{-1}(1),\dots ,w^{-1}(n))\in \mathbb {R}^n$
, and let
$v_w = -(w^{-1}(1),\dots ,w^{-1}(n))\in \mathbb {R}^n$
, and let
![]() $P_n := \mathrm {conv}(v_w\mid w\in S_n)$
be the standard permutohedron in
$P_n := \mathrm {conv}(v_w\mid w\in S_n)$
be the standard permutohedron in
![]() $\mathbb {R}^n$
. For the following result, see [Reference Postnikov, Reiner and WilliamsPRW, Theorem 15.3] and [Reference Castillo and LiuCL].
$\mathbb {R}^n$
. For the following result, see [Reference Postnikov, Reiner and WilliamsPRW, Theorem 15.3] and [Reference Castillo and LiuCL].
Theorem 3.2. The following are equivalent for a polytope P in
![]() $\mathbb {R}^n$
:
$\mathbb {R}^n$
:
-
1. The polytope P is a generalized permutohedron.
-
2. The normal fan of P is a coarsening of the normal fan of the standard permutohedron
 $P_n$
.
$P_n$
. -
3. The vertices of P can be (possibly redundantly) labelled
 $v_w'$
,
$v_w'$
,
 $w\in S_n$
, such that for any edge
$w\in S_n$
, such that for any edge
 $(v_u,v_w)$
in
$(v_u,v_w)$
in
 $P_n$
, there is a nonnegative real t, such that
$P_n$
, there is a nonnegative real t, such that
 $(v_u' - v_w') = t(v_u-v_w)$
.
$(v_u' - v_w') = t(v_u-v_w)$
.
For a polytope P, we define the support function
![]() $f_P: (\mathbb {R}^n)^* \to \mathbb {R}$
given by
$f_P: (\mathbb {R}^n)^* \to \mathbb {R}$
given by
The function
![]() $f_P$
is a piecewise linear function on
$f_P$
is a piecewise linear function on
![]() $(\mathbb {R}^n)^*$
whose maximal domains of linearity are exactly the top-dimensional cones of the normal fan of P.
$(\mathbb {R}^n)^*$
whose maximal domains of linearity are exactly the top-dimensional cones of the normal fan of P.
The normal fan of the standard permutohedron
![]() $P_n$
is the braid fan (see Section 8.5), and by Theorem 3.2(2), a generalized permutohedron P is uniquely determined by the values
$P_n$
is the braid fan (see Section 8.5), and by Theorem 3.2(2), a generalized permutohedron P is uniquely determined by the values
![]() $f_P(S):= f_P(h_S)$
, where
$f_P(S):= f_P(h_S)$
, where
![]() $h_S(x_1,\ldots ,x_n)= \sum _{i \in S} x_i$
, and S varies over proper nonempty subsets of
$h_S(x_1,\ldots ,x_n)= \sum _{i \in S} x_i$
, and S varies over proper nonempty subsets of
![]() $[n]$
. The polytope P is then given by
$[n]$
. The polytope P is then given by
We write
![]() $f_P|_{2^{[n]}}$
for the function sending a subset
$f_P|_{2^{[n]}}$
for the function sending a subset
![]() $S \subset [n]$
to
$S \subset [n]$
to
![]() $f_P(S)$
, and, more generally, we will use notation, such as
$f_P(S)$
, and, more generally, we will use notation, such as
![]() $f_P|_{\mathcal {S}}$
for a collection
$f_P|_{\mathcal {S}}$
for a collection
![]() ${\mathcal {S}} \subseteq 2^{[n]}$
of subsets.
${\mathcal {S}} \subseteq 2^{[n]}$
of subsets.
3.2. Alcoved polytopes
Let
![]() $h_1,\dots ,h_n$
be the basis of
$h_1,\dots ,h_n$
be the basis of
![]() $(\mathbb {R}^n)^*$
, such that
$(\mathbb {R}^n)^*$
, such that
![]() $h_i(x) = x_1 + x_2 + \cdots + x_i$
. Thus,
$h_i(x) = x_1 + x_2 + \cdots + x_i$
. Thus,
![]() $h_i:= h_{[1,i]}$
.
$h_i:= h_{[1,i]}$
.
Definition 3.3 [Reference Lam and PostnikovLP07]
A polytope
![]() $P\subset \mathbb {R}^n$
is called an alcoved polytope if it is given by inequalities of the form
$P\subset \mathbb {R}^n$
is called an alcoved polytope if it is given by inequalities of the form
and the equation
![]() $x_1 + \cdots + x_n = k$
, for some realFootnote 1 numbers
$x_1 + \cdots + x_n = k$
, for some realFootnote 1 numbers
![]() $a_{ij}$
and k.
$a_{ij}$
and k.
Alcoved polytopes are also called polytropes in [Reference Joswig and KulasJK]. We will always assume in (3.2) that the
![]() $a_{ij}$
have been chosen to be minimal, that is, they are values of the support function.
$a_{ij}$
have been chosen to be minimal, that is, they are values of the support function.
Lemma 3.4. The set of alcoved polytopes in the affine hyperplane
![]() $H_k$
and the set of alcoved polytopes in
$H_k$
and the set of alcoved polytopes in
![]() $H_{\ell }$
are in natural bijection via the isomorphism
$H_{\ell }$
are in natural bijection via the isomorphism
![]() $+(\ell {-}k) e_1: H_k \to H_{\ell }$
adding
$+(\ell {-}k) e_1: H_k \to H_{\ell }$
adding
![]() $(\ell -k)$
to the first coordinate. This bijection preserves the values of
$(\ell -k)$
to the first coordinate. This bijection preserves the values of
![]() $a_{ij}$
.
$a_{ij}$
.
An alcoved polytope P is called generic if it is full-dimensional in H, and each equality
![]() $(h_i - h_j)(x) = a_{ij}$
defines a facet of P, for all
$(h_i - h_j)(x) = a_{ij}$
defines a facet of P, for all
![]() $i,j\in [n]$
,
$i,j\in [n]$
,
![]() $i \neq j$
.
$i \neq j$
.
Definition 3.5. Let
![]() $Q \subset H$
be a bounded subset. The alcoved envelope
$Q \subset H$
be a bounded subset. The alcoved envelope
![]() $\mathrm {env}(Q)\subset H$
is defined to be the smallest alcoved polytope containing Q. Equivalently,
$\mathrm {env}(Q)\subset H$
is defined to be the smallest alcoved polytope containing Q. Equivalently,
![]() $\mathrm {env}(Q)$
is given by inequalities (3.2), where
$\mathrm {env}(Q)$
is given by inequalities (3.2), where
![]() $a_{ij}=\mathrm {supremum}_{x\in Q} (h_i-h_j)(x)$
.
$a_{ij}=\mathrm {supremum}_{x\in Q} (h_i-h_j)(x)$
.
Example 3.6. For
![]() $n=3$
, the class of generalized permutohedra coincides with the class of alcoved polytopes. However, for
$n=3$
, the class of generalized permutohedra coincides with the class of alcoved polytopes. However, for
![]() $n\geq 4$
, neither of these two classes of polytopes contains the other. For example, the standard permutohedron
$n\geq 4$
, neither of these two classes of polytopes contains the other. For example, the standard permutohedron
![]() $P_4 = \mathrm {conv}((w(1),w(2),w(3),w(4))\mid w\in S_4)\subset \mathbb {R}^4$
is a generalized permutohedron, but it is not an alcoved polytope, because one of its facets is given by
$P_4 = \mathrm {conv}((w(1),w(2),w(3),w(4))\mid w\in S_4)\subset \mathbb {R}^4$
is a generalized permutohedron, but it is not an alcoved polytope, because one of its facets is given by
![]() $x_1 + x_3 \leq 7$
. On the other hand, the simplex
$x_1 + x_3 \leq 7$
. On the other hand, the simplex
![]() $\mathrm {conv}(e_1 + e_3,\, e_2 + e_3,\, e_2+e_4,\, e_3+e_4)\subset \mathbb {R}^4$
is an alcoved polytope, but it is not a generalized permutohedron, because it has the edge
$\mathrm {conv}(e_1 + e_3,\, e_2 + e_3,\, e_2+e_4,\, e_3+e_4)\subset \mathbb {R}^4$
is an alcoved polytope, but it is not a generalized permutohedron, because it has the edge
![]() $(e_1+e_3,\,e_2 + e_4)$
. Here, “conv” means the convex hull of points.
$(e_1+e_3,\,e_2 + e_4)$
. Here, “conv” means the convex hull of points.
Define the cyclic interval
![]() $[r,s]$
in
$[r,s]$
in
![]() $[n]$
as
$[n]$
as
 $$ \begin{align*}[r,s]:=\left\{\begin{array}{ll} \{r,r+1,\dots,s\}&\text{if } 1\leq r\leq s \leq n,\\ \{r,r+1,\dots,n,1,2,\dots,s\}&\text{if } 1\leq s < r \leq n. \end{array} \right\} ,\end{align*} $$
$$ \begin{align*}[r,s]:=\left\{\begin{array}{ll} \{r,r+1,\dots,s\}&\text{if } 1\leq r\leq s \leq n,\\ \{r,r+1,\dots,n,1,2,\dots,s\}&\text{if } 1\leq s < r \leq n. \end{array} \right\} ,\end{align*} $$
and set
![]() $h_{[r,s]}:= \sum _{i \in [r,s]} x_i \in (\mathbb {R}^n)^*$
. Alcoved polytopes P are exactly all polytopes of the form
$h_{[r,s]}:= \sum _{i \in [r,s]} x_i \in (\mathbb {R}^n)^*$
. Alcoved polytopes P are exactly all polytopes of the form
for cyclic intervals
![]() $[r,s]\subset [n]$
, where
$[r,s]\subset [n]$
, where
![]() $f_{[r,s]}= f_P([r,s]):= f_P(h_{[r,s]})$
. Note that we have
$f_{[r,s]}= f_P([r,s]):= f_P(h_{[r,s]})$
. Note that we have
 $$ \begin{align} a_{ij} = \begin{cases} f_{[j+1,i]} &\mbox{if } i> j \\ f_{[j+1,i]} -f_{[n]} = f_{[j+1,i]} -k& \mbox{if } i < j ,\end{cases} \end{align} $$
$$ \begin{align} a_{ij} = \begin{cases} f_{[j+1,i]} &\mbox{if } i> j \\ f_{[j+1,i]} -f_{[n]} = f_{[j+1,i]} -k& \mbox{if } i < j ,\end{cases} \end{align} $$
and it will be convenient to use both sets of parameters
![]() $f_{[r,s]}$
and
$f_{[r,s]}$
and
![]() $a_{ij}$
.
$a_{ij}$
.
If
![]() $x =(x_1,x_2,\ldots ,x_n) \in \mathbb {R}^n$
, we shall use the shorthands
$x =(x_1,x_2,\ldots ,x_n) \in \mathbb {R}^n$
, we shall use the shorthands
![]() $x_{[r,s]} := h_{[r,s]}(x)= \sum _{i \in [r,s]} x_i$
and
$x_{[r,s]} := h_{[r,s]}(x)= \sum _{i \in [r,s]} x_i$
and
![]() $x_S:= h_S(x) = \sum _{i \in S} x_i$
.
$x_S:= h_S(x) = \sum _{i \in S} x_i$
.
Remark 3.7. The class of generalized permutohedra in
![]() $\mathbb {R}^n$
is closed under the operation of taking the Minkowski sum polytopes, but is not closed under the operation of taking the intersection of polytopes. On the other hand, the class of alcoved polytopes in
$\mathbb {R}^n$
is closed under the operation of taking the Minkowski sum polytopes, but is not closed under the operation of taking the intersection of polytopes. On the other hand, the class of alcoved polytopes in
![]() $\mathbb {R}^n$
is closed under the operation of taking the intersection of polytopes (if it is nonempty), but is not closed under the operation of taking the Minkowski sum of polytopes.
$\mathbb {R}^n$
is closed under the operation of taking the intersection of polytopes (if it is nonempty), but is not closed under the operation of taking the Minkowski sum of polytopes.
3.3. Polypositroids
Definition 3.8. A polypositroid is a polytope
![]() $P\subset H_k$
which is both a generalized permutohedron and an alcoved polytope.
$P\subset H_k$
which is both a generalized permutohedron and an alcoved polytope.
As for alcoved polytopes, polypositroids in
![]() $H_k$
and in
$H_k$
and in
![]() $H_{\ell }$
are naturally in bijection. One of the main results of this paper is an explicit parametrization of all polypositroids.
$H_{\ell }$
are naturally in bijection. One of the main results of this paper is an explicit parametrization of all polypositroids.
We give some examples of polypositroids. For
![]() $a \in \mathbb {R}$
and P a polytope, the notation
$a \in \mathbb {R}$
and P a polytope, the notation
![]() $aP$
denotes the polytope
$aP$
denotes the polytope
![]() $\{ax \mid x \in P\}$
. For a cyclic interval
$\{ax \mid x \in P\}$
. For a cyclic interval
![]() $[r,s]$
, let
$[r,s]$
, let
denote the corresponding coordinate simplex.
The cyclohedron is the Minkowski sum of simplices
where each
![]() $c_{r,s}> 0$
and
$c_{r,s}> 0$
and
![]() $b> 0$
. By [Reference PostnikovPo09, Theorem 7.4], the cyclohedron P is both an alcoved polytope and a generalized permutohedron, and in addition, P is simple. The
$b> 0$
. By [Reference PostnikovPo09, Theorem 7.4], the cyclohedron P is both an alcoved polytope and a generalized permutohedron, and in addition, P is simple. The
![]() $f_{[r,s]}$
from (3.3) are given by
$f_{[r,s]}$
from (3.3) are given by
and we also set
![]() $k:= b+ \sum c_{r,s}$
so that
$k:= b+ \sum c_{r,s}$
so that
![]() $P \subset H_k$
.
$P \subset H_k$
.
If we set
![]() $c_{r,s} = 0$
whenever
$c_{r,s} = 0$
whenever
![]() $r>s$
(i.e., whenever
$r>s$
(i.e., whenever
![]() $[r,s]$
is not an honest interval), then we obtain the associahedron, which is also a polypositroid. Another possibility is to consider the polytope
$[r,s]$
is not an honest interval), then we obtain the associahedron, which is also a polypositroid. Another possibility is to consider the polytope
![]() $P(b,c_{r,s})$
defined by (3.5), where we allow
$P(b,c_{r,s})$
defined by (3.5), where we allow
![]() $b \in \mathbb {R}$
and
$b \in \mathbb {R}$
and
![]() $c_{r,s} \geq 0$
. When
$c_{r,s} \geq 0$
. When
![]() $b < 0$
, we use the Minkowski difference:
$b < 0$
, we use the Minkowski difference:
It is not hard to see that the deformed cyclohedron
![]() $P(b,c_{r,s})$
is either empty, or a polypositroid. When
$P(b,c_{r,s})$
is either empty, or a polypositroid. When
![]() $b \geq 0$
, the polytope
$b \geq 0$
, the polytope
![]() $P(b,c_{r,s})$
is a deformation of a cyclohedron: the normal fan of
$P(b,c_{r,s})$
is a deformation of a cyclohedron: the normal fan of
![]() $P(b,c_{r,s})$
is a coarsening of that of the cyclohedron. However, when
$P(b,c_{r,s})$
is a coarsening of that of the cyclohedron. However, when
![]() $b < 0$
, this may no longer be the case.
$b < 0$
, this may no longer be the case.
4. The cone of polypositroids
The numbers
![]() $f_P(S)$
in (3.1) are not arbitrary. It is well-known that support functions of generalized permutohedra are exactly the submodular functions, for example, see [Reference Morton, Pachter, Shiu, Sturmfels and WienandMPS2W, Proposition 12], [Reference Aguiar and ArdilaA2, Section 12], [Reference Castillo and LiuCL, Theorem 3.11].
$f_P(S)$
in (3.1) are not arbitrary. It is well-known that support functions of generalized permutohedra are exactly the submodular functions, for example, see [Reference Morton, Pachter, Shiu, Sturmfels and WienandMPS2W, Proposition 12], [Reference Aguiar and ArdilaA2, Section 12], [Reference Castillo and LiuCL, Theorem 3.11].
Theorem 4.1. The polytope P given by (3.1
) is a generalized permutohedron if and only if
![]() $f_P$
is submodular, that is
$f_P$
is submodular, that is
for any subsets
![]() $S,T \subset [n]$
, where we assume that
$S,T \subset [n]$
, where we assume that
![]() $f_P(\emptyset ) = 0$
.
$f_P(\emptyset ) = 0$
.
Definition 4.2. The submodular cone, or the cone of generalized permutohedra, is the cone
![]() ${\mathcal {C}}_{\mathrm {sub}}$
of all functions
${\mathcal {C}}_{\mathrm {sub}}$
of all functions
![]() $f :2^{[n]} \to \mathbb {R}$
satisfying (4.1).
$f :2^{[n]} \to \mathbb {R}$
satisfying (4.1).
The cone structure of
![]() ${\mathcal {C}}_{\mathrm {sub}}$
corresponds to taking Minkowski sums of generalized permutohedra. Let us now turn to alcoved polytopes.
${\mathcal {C}}_{\mathrm {sub}}$
corresponds to taking Minkowski sums of generalized permutohedra. Let us now turn to alcoved polytopes.
Theorem 4.3. Suppose
![]() $n \geq 3$
. Let P be an alcoved polytope given by (3.2) (with
$n \geq 3$
. Let P be an alcoved polytope given by (3.2) (with
![]() $a_{ij}$
minimal). Then the
$a_{ij}$
minimal). Then the
![]() $a_{ij}$
satisfy the triangle inequality
$a_{ij}$
satisfy the triangle inequality
for distinct
![]() $i,j,k \in [n]$
. Conversely, any
$i,j,k \in [n]$
. Conversely, any
![]() $a_{ij}$
satisfying (4.2) define a (nonempty) alcoved polytope in
$a_{ij}$
satisfying (4.2) define a (nonempty) alcoved polytope in
![]() $H_k$
.
$H_k$
.
For example, for
![]() $n = 3$
, we have six inequalities (4.2):
$n = 3$
, we have six inequalities (4.2):
![]() $a_{12}+a_{23} \geq a_{13}$
,
$a_{12}+a_{23} \geq a_{13}$
,
![]() $a_{13}+a_{32} \geq a_{12}$
,
$a_{13}+a_{32} \geq a_{12}$
,
![]() $a_{21}+a_{13} \geq a_{23}$
,
$a_{21}+a_{13} \geq a_{23}$
,
![]() $a_{23}+a_{31} \geq a_{21}$
,
$a_{23}+a_{31} \geq a_{21}$
,
![]() $a_{31}+a_{12} \geq a_{32}$
, and
$a_{31}+a_{12} \geq a_{32}$
, and
![]() $a_{32}+a_{21} \geq a_{31}$
.
$a_{32}+a_{21} \geq a_{31}$
.
We thank Michael Joswig for pointing out that Theorem 4.3 is known to the optimization community (see [Reference Joswig and LohoJL, Reference JoswigJos] and the references therein).
Proposition 4.4. Let
![]() $n \geq 3$
. Let P be an alcoved polytope given by the inequalities
$n \geq 3$
. Let P be an alcoved polytope given by the inequalities
![]() $(h_i - h_j)(x) \leq a_{ij}$
. Then P is generic if and only if, for any three pairwise distinct indices
$(h_i - h_j)(x) \leq a_{ij}$
. Then P is generic if and only if, for any three pairwise distinct indices
![]() $i, j, k \in [n]$
, we have the strict triangle inequality
$i, j, k \in [n]$
, we have the strict triangle inequality
![]() $a_{ij} + a_{jk}> a_{ik}$
.
$a_{ij} + a_{jk}> a_{ik}$
.
Proof. The “only if” direction is trivial. We prove the “if” direction. Let P denote the “alcoved polyhedron” inside
![]() $\mathbb {R}^n$
given by the inequalities
$\mathbb {R}^n$
given by the inequalities
![]() $(h_i - h_j)(x) \leq a_{ij}$
. The intersections
$(h_i - h_j)(x) \leq a_{ij}$
. The intersections
![]() $P \cap H_k$
for varying k are linearly isomorphic via Lemma 3.4. Thus, it suffices to show that P itself is generic.
$P \cap H_k$
for varying k are linearly isomorphic via Lemma 3.4. Thus, it suffices to show that P itself is generic.
Since
![]() $n \geq 3$
, summing
$n \geq 3$
, summing
![]() $a_{cd}+a_{de}> a_{ce}$
and
$a_{cd}+a_{de}> a_{ce}$
and
![]() $a_{dc}+a_{ce}> a_{de}$
for distinct
$a_{dc}+a_{ce}> a_{de}$
for distinct
![]() $c,d,e$
, we obtain
$c,d,e$
, we obtain
![]() $a_{cd} + a_{dc}> 0$
. It follows that P is not strictly contained in any hyperplane
$a_{cd} + a_{dc}> 0$
. It follows that P is not strictly contained in any hyperplane
![]() $(h_c-h_d)(x) = a_{cd}$
, and therefore P is full-dimensional.
$(h_c-h_d)(x) = a_{cd}$
, and therefore P is full-dimensional.
Fix
![]() $ c\neq d$
, and let
$ c\neq d$
, and let
![]() $A = \{x \in \mathbb {R}^n \mid (h_c-h_d)(x) = a_{cd}\}$
. To show that
$A = \{x \in \mathbb {R}^n \mid (h_c-h_d)(x) = a_{cd}\}$
. To show that
![]() $P \cap A$
is a facet of P, it suffices to show that
$P \cap A$
is a facet of P, it suffices to show that
![]() $P \cap A \neq \emptyset $
because, by the same reasoning as above,
$P \cap A \neq \emptyset $
because, by the same reasoning as above,
![]() $P \cap A$
would be full-dimensional in A.
$P \cap A$
would be full-dimensional in A.
For
![]() $x \in \mathbb {R}^n$
, define
$x \in \mathbb {R}^n$
, define
Thus,
![]() $x \in P$
if and only if
$x \in P$
if and only if
![]() $d_P(x) = 0$
. Since the function
$d_P(x) = 0$
. Since the function
![]() $d_P$
is continuous, it is straightforward to see that it achieves a minimum on A. Let
$d_P$
is continuous, it is straightforward to see that it achieves a minimum on A. Let
![]() $v \in A$
be such a minimum, and assume
$v \in A$
be such a minimum, and assume
![]() $d_P(v)> 0$
. We also assume that v is chosen so that
$d_P(v)> 0$
. We also assume that v is chosen so that
is minimal. Note that since
![]() $v \in A$
, we have
$v \in A$
, we have
![]() $(c,d) \notin R(v)$
. It follows from
$(c,d) \notin R(v)$
. It follows from
![]() $a_{cd} + a_{dc}> 0$
that
$a_{cd} + a_{dc}> 0$
that
![]() $(d,c) \notin R(v)$
.
$(d,c) \notin R(v)$
.
Suppose
![]() $(e,f) \in R(v)$
. Assume that
$(e,f) \in R(v)$
. Assume that
![]() $e \notin \{c,d\}$
; the case
$e \notin \{c,d\}$
; the case
![]() $f \notin \{c,d\}$
is similar. If there does not exist
$f \notin \{c,d\}$
is similar. If there does not exist
![]() $(g,e) \in R(v)$
, then we can modify v slightly so that
$(g,e) \in R(v)$
, then we can modify v slightly so that
![]() $h_e(v)$
decreases but the other
$h_e(v)$
decreases but the other
![]() $h_{e'}(v)$
remain unchanged, and reducing the size of
$h_{e'}(v)$
remain unchanged, and reducing the size of
![]() $R(v)$
. This would contradict the construction of v. But if
$R(v)$
. This would contradict the construction of v. But if
![]() $(g,e) \in R(v)$
, then using the condition of the proposition, we have
$(g,e) \in R(v)$
, then using the condition of the proposition, we have
![]() $(h_g-h_f)(v) = (h_g-h_e)(v) + (h_e-h_f)(v) = a_{ge}+a_{ef} + 2d_P(v)> a_{gf}+d_P(v)$
, contradicting the definition of
$(h_g-h_f)(v) = (h_g-h_e)(v) + (h_e-h_f)(v) = a_{ge}+a_{ef} + 2d_P(v)> a_{gf}+d_P(v)$
, contradicting the definition of
![]() $d_P(v)$
. Thus, we conclude that
$d_P(v)$
. Thus, we conclude that
![]() $d_P(v) = 0$
, as desired.
$d_P(v) = 0$
, as desired.
Proof of Theorem 4.3
By our assumption that the
![]() $a_{ij}$
-s are taken minimal, it is clear that (4.2) holds for any alcoved polytope. By Proposition 4.4, the inequalities
$a_{ij}$
-s are taken minimal, it is clear that (4.2) holds for any alcoved polytope. By Proposition 4.4, the inequalities
![]() $a_{ij} + a_{jk}> a_{ik}$
define an open cone
$a_{ij} + a_{jk}> a_{ik}$
define an open cone
![]() $C \subset \mathbb {R}^{n(n-1)}$
, each point of which represents a generic alcoved polytope. It follows from (3.6) that C is nonempty: the cyclohedron is a generic alcoved polytope. The closure of C is thus the closed cone cut out by (4.2). The corresponding limits of generic alcoved polytopes are nonempty alcoved polytopes, finishing the proof of the theorem.
$C \subset \mathbb {R}^{n(n-1)}$
, each point of which represents a generic alcoved polytope. It follows from (3.6) that C is nonempty: the cyclohedron is a generic alcoved polytope. The closure of C is thus the closed cone cut out by (4.2). The corresponding limits of generic alcoved polytopes are nonempty alcoved polytopes, finishing the proof of the theorem.
Definition 4.5. The triangle inequality cone, or the cone of alcoved polytopes, is the cone
![]() ${\mathcal {C}}_{\mathrm {alc}} \subset \mathbb {R}^{n(n-1)}$
of all
${\mathcal {C}}_{\mathrm {alc}} \subset \mathbb {R}^{n(n-1)}$
of all
![]() $a_{ij}$
satisfying (4.2).
$a_{ij}$
satisfying (4.2).
Remark 4.6. We caution the reader that the cone
![]() ${\mathcal {C}}_{\mathrm {sub}}$
contains the information
${\mathcal {C}}_{\mathrm {sub}}$
contains the information
![]() $f_P([n]) = k$
and thus parametrizes generalized permutohedra in various affine hyperplanes
$f_P([n]) = k$
and thus parametrizes generalized permutohedra in various affine hyperplanes
![]() $H_k$
. In contrast, an alcoved polytope is determined by a point in
$H_k$
. In contrast, an alcoved polytope is determined by a point in
![]() ${\mathcal {C}}_{\mathrm {alc}}$
together with the value of k. Equivalently,
${\mathcal {C}}_{\mathrm {alc}}$
together with the value of k. Equivalently,
![]() ${\mathcal {C}}_{\mathrm {alc}}$
is the cone of alcoved polytopes inside
${\mathcal {C}}_{\mathrm {alc}}$
is the cone of alcoved polytopes inside
![]() $H_0$
.
$H_0$
.
The cone structure of
![]() ${\mathcal {C}}_{\mathrm {alc}}$
corresponds to the composition of the following two operations: first take the Minkowski sum
${\mathcal {C}}_{\mathrm {alc}}$
corresponds to the composition of the following two operations: first take the Minkowski sum
![]() $P_1 + P_2$
of two alcoved polytopes, and then take the alcoved envelope
$P_1 + P_2$
of two alcoved polytopes, and then take the alcoved envelope
![]() $\mathrm {env}(P_1+P_2)$
(see Definition 3.5).
$\mathrm {env}(P_1+P_2)$
(see Definition 3.5).
Definition 4.7. The polypositroid cone
![]() ${\mathcal {C}}_{\mathrm {pol}} \subset {\mathcal {C}}_{\mathrm {alc}}$
is the subset of
${\mathcal {C}}_{\mathrm {pol}} \subset {\mathcal {C}}_{\mathrm {alc}}$
is the subset of
![]() ${\mathcal {C}}_{\mathrm {alc}}$
representing alcoved polytopes that are polypositroids.
${\mathcal {C}}_{\mathrm {alc}}$
representing alcoved polytopes that are polypositroids.
The fact that
![]() ${\mathcal {C}}_{\mathrm {pol}}$
is closed under the addition and positive scalar multiplication is a consequence of Theorems 4.8 or 4.9 below. Let
${\mathcal {C}}_{\mathrm {pol}}$
is closed under the addition and positive scalar multiplication is a consequence of Theorems 4.8 or 4.9 below. Let
![]() $\mathcal {I} \subset 2^{[n]}$
denote the collection of all nonempty cyclic intervals, including
$\mathcal {I} \subset 2^{[n]}$
denote the collection of all nonempty cyclic intervals, including
![]() $[n]$
itself. We define a map
$[n]$
itself. We define a map
![]() $\pi _{\mathcal {I}}: \mathbb {R}^{2^{[n]}} \to \mathbb {R}^{\mathcal {I}} \simeq \mathbb {R}^{n(n-1)}$
by first projecting to cyclic intervals, and then applying the transformation (3.4). If
$\pi _{\mathcal {I}}: \mathbb {R}^{2^{[n]}} \to \mathbb {R}^{\mathcal {I}} \simeq \mathbb {R}^{n(n-1)}$
by first projecting to cyclic intervals, and then applying the transformation (3.4). If
![]() $f_P$
is the support function of a generalized permutohedron P, considered as an element of
$f_P$
is the support function of a generalized permutohedron P, considered as an element of
![]() $\mathbb {R}^{2^{[n]}}$
, then
$\mathbb {R}^{2^{[n]}}$
, then
![]() $\pi _{\mathcal {I}}(f_P)$
represents the alcoved envelope
$\pi _{\mathcal {I}}(f_P)$
represents the alcoved envelope
![]() $\mathrm {env}(P)$
of P (Definition 3.5).
$\mathrm {env}(P)$
of P (Definition 3.5).
Theorem 4.8. We have
![]() $\pi _{\mathcal {I}}({\mathcal {C}}_{\mathrm {sub}}) = {\mathcal {C}}_{\mathrm {pol}}$
.
$\pi _{\mathcal {I}}({\mathcal {C}}_{\mathrm {sub}}) = {\mathcal {C}}_{\mathrm {pol}}$
.
Theorem 4.8 will be proved in Section 6.6. Note that
![]() $\pi _{\mathcal {I}}: {\mathcal {C}}_{\mathrm {sub}} \to {\mathcal {C}}_{\mathrm {pol}}$
is a homomorphism of cones: it commutes with addition and with scalar multiplication, and sends
$\pi _{\mathcal {I}}: {\mathcal {C}}_{\mathrm {sub}} \to {\mathcal {C}}_{\mathrm {pol}}$
is a homomorphism of cones: it commutes with addition and with scalar multiplication, and sends
![]() $0$
to
$0$
to
![]() $0$
.
$0$
.
Theorem 4.9. The cone
![]() ${\mathcal {C}}_{\mathrm {pol}}$
is the subcone of
${\mathcal {C}}_{\mathrm {pol}}$
is the subcone of
![]() ${\mathcal {C}}_{\mathrm {alc}}$
satisfying
${\mathcal {C}}_{\mathrm {alc}}$
satisfying
for any four indices
![]() $i,j,k,l$
in cyclic order.
$i,j,k,l$
in cyclic order.
Theorem 4.9 will be proved in Section 8.3.
Remark 4.11. We have described the three cones
![]() ${\mathcal {C}}_{\mathrm {sub}}, {\mathcal {C}}_{\mathrm {alc}}, {\mathcal {C}}_{\mathrm { pol}}$
in terms of defining (possibly redundant) inequalities. The extremal rays of
${\mathcal {C}}_{\mathrm {sub}}, {\mathcal {C}}_{\mathrm {alc}}, {\mathcal {C}}_{\mathrm { pol}}$
in terms of defining (possibly redundant) inequalities. The extremal rays of
![]() ${\mathcal {C}}_{\mathrm {sub}}$
(modulo translation) are hard to describe explicitly (see, e.g. [Reference NguyenNg, Reference Morton, Pachter, Shiu, Sturmfels and WienandMPS2W, Reference Ardila, Castillo, Eur and PostnikovACEP] for discussions of the rays). Among the rays of
${\mathcal {C}}_{\mathrm {sub}}$
(modulo translation) are hard to describe explicitly (see, e.g. [Reference NguyenNg, Reference Morton, Pachter, Shiu, Sturmfels and WienandMPS2W, Reference Ardila, Castillo, Eur and PostnikovACEP] for discussions of the rays). Among the rays of
![]() ${\mathcal {C}}_{\mathrm {sub}}$
are all connected matroids [Reference NguyenNg].
${\mathcal {C}}_{\mathrm {sub}}$
are all connected matroids [Reference NguyenNg].
However, we will give in Corollary 6.14 an explicit description of the rays of
![]() ${\mathcal {C}}_{\mathrm { pol}}$
(modulo translation).
${\mathcal {C}}_{\mathrm { pol}}$
(modulo translation).
5. Alcoved envelopes
Let
![]() $C \subset H_0 \subset \mathbb {R}^n$
denote the following polyhedral
$C \subset H_0 \subset \mathbb {R}^n$
denote the following polyhedral
![]() $(n-1)$
-dimensional pointed cone
$(n-1)$
-dimensional pointed cone
Define the dominance order on the hyperplane
![]() $H=H_k$
as the partial order
$H=H_k$
as the partial order
![]() $x \preceq y$
if and only if
$x \preceq y$
if and only if
![]() $x_1 \leq y_1$
,
$x_1 \leq y_1$
,
![]() $x_1 + x_2 \leq y_1 + y_2$
,
$x_1 + x_2 \leq y_1 + y_2$
,
![]() $\ldots $
, or equivalently,
$\ldots $
, or equivalently,
![]() $x-y \in C$
. For any bounded subset
$x-y \in C$
. For any bounded subset
![]() $Q\subset H$
, there is a unique maximal in the dominance order point
$Q\subset H$
, there is a unique maximal in the dominance order point
![]() $v=v(Q)\in H$
, such that
$v=v(Q)\in H$
, such that
![]() $Q\subset v + C$
. Informally,
$Q\subset v + C$
. Informally,
![]() $v+C$
is the cone containing Q, such that every facet of
$v+C$
is the cone containing Q, such that every facet of
![]() $v+C$
touches Q. Note that the cone C is an alcoved polyhedron: its facets have normals given by
$v+C$
touches Q. Note that the cone C is an alcoved polyhedron: its facets have normals given by
![]() $h_i-h_n$
.
$h_i-h_n$
.
Let
![]() $c = (12\cdots n) \in S_n$
be the long cycle, with
$c = (12\cdots n) \in S_n$
be the long cycle, with
![]() $c = 23 \cdots n1$
in one-line notation. The permutations
$c = 23 \cdots n1$
in one-line notation. The permutations
![]() $w \in S_n$
act on
$w \in S_n$
act on
![]() $\mathbb {R}^n$
by the formula
$\mathbb {R}^n$
by the formula
Then c acts on
![]() $\mathbb {R}^n$
as the cyclic shift linear operator given by
$\mathbb {R}^n$
as the cyclic shift linear operator given by
![]() $c(e_i) = e_{i+1}$
, for
$c(e_i) = e_{i+1}$
, for
![]() $i=1,\dots ,n$
(here and below, we assume that indices i are taken modulo n). For
$i=1,\dots ,n$
(here and below, we assume that indices i are taken modulo n). For
![]() $i \in \mathbb {Z}/n\mathbb {Z}$
, define the cyclically shifted cone
$i \in \mathbb {Z}/n\mathbb {Z}$
, define the cyclically shifted cone
![]() $C_i := c^{i-1}(C)$
. Thus,
$C_i := c^{i-1}(C)$
. Thus,
![]() $C_1 = C$
.
$C_1 = C$
.
If
![]() $\mathbf {v} = (v^{(1)},\ldots ,v^{(n)})$
is a sequence of points in H, we denote by
$\mathbf {v} = (v^{(1)},\ldots ,v^{(n)})$
is a sequence of points in H, we denote by
![]() $Q(\mathbf {v})$
the intersection
$Q(\mathbf {v})$
the intersection
It is clear that
![]() $Q(\mathbf {v})$
is an alcoved polytope whenever it is nonempty.
$Q(\mathbf {v})$
is an alcoved polytope whenever it is nonempty.
For a bounded subset
![]() $Q\subset H$
, define
$Q\subset H$
, define
Again, the cone
![]() $v^{(i)} + C_i$
contains Q, and every facet of
$v^{(i)} + C_i$
contains Q, and every facet of
![]() $v^{(i)} + C_i$
touches Q. Recall the alcoved envelope
$v^{(i)} + C_i$
touches Q. Recall the alcoved envelope
![]() $\mathrm {env}(Q)$
defined in Definition 3.5.
$\mathrm {env}(Q)$
defined in Definition 3.5.
Lemma 5.1. For the cones
![]() $C_i$
and points
$C_i$
and points
![]() $v^{(i)}$
,
$v^{(i)}$
,
![]() $i \in \mathbb {Z}/n\mathbb {Z}$
, as above, the alcoved envelope of Q is the intersection of the following cones
$i \in \mathbb {Z}/n\mathbb {Z}$
, as above, the alcoved envelope of Q is the intersection of the following cones
Proof. Let
![]() $f_{[r,s]}$
be the minimal number, such that Q belongs to the halfspace
$f_{[r,s]}$
be the minimal number, such that Q belongs to the halfspace
![]() $S_{[r,s]}=\{x\in H\mid \sum _{i\in [r,s]} x_i \leq f_{[r,s]}\}$
, that is the (unique) facet of
$S_{[r,s]}=\{x\in H\mid \sum _{i\in [r,s]} x_i \leq f_{[r,s]}\}$
, that is the (unique) facet of
![]() $S_{[r,s]}$
touches Q. Then the alcoved envelope of Q is the alcoved polytope
$S_{[r,s]}$
touches Q. Then the alcoved envelope of Q is the alcoved polytope
![]() $\mathrm {env}(Q) = \bigcap _{r,s} S_{[r,s]}$
. For fixed r, the intersection
$\mathrm {env}(Q) = \bigcap _{r,s} S_{[r,s]}$
. For fixed r, the intersection
![]() $\bigcap _{s} S_{[r,s]}$
is the affine translation
$\bigcap _{s} S_{[r,s]}$
is the affine translation
![]() $v^{(r)} + C_r$
of the cone
$v^{(r)} + C_r$
of the cone
![]() $C_r$
that satisfies the conditions of the lemma. So
$C_r$
that satisfies the conditions of the lemma. So
![]() $\mathrm {env}(Q) = \bigcap _{r \in \mathbb {Z}/n\mathbb {Z}} (v^{(r)}+C_r)$
, as needed.
$\mathrm {env}(Q) = \bigcap _{r \in \mathbb {Z}/n\mathbb {Z}} (v^{(r)}+C_r)$
, as needed.
6. Parametrization of polypositroids
6.1. Coxeter necklaces
As before, we fix an affine plane
![]() $H=H_k:=\{x \in \mathbb {R}^n \mid x_1 + \cdots + x_n = k\}$
.
$H=H_k:=\{x \in \mathbb {R}^n \mid x_1 + \cdots + x_n = k\}$
.
Definition 6.1. Let
![]() $\mathbf {v} = (v^{(1)},v^{(2)},\ldots ,v^{(n)})$
be a sequence of points in H. We say that
$\mathbf {v} = (v^{(1)},v^{(2)},\ldots ,v^{(n)})$
be a sequence of points in H. We say that
![]() $\mathbf {v}$
is a Coxeter necklace if, for each i, we have
$\mathbf {v}$
is a Coxeter necklace if, for each i, we have
Here, the superscript i is taken modulo n. Since
![]() $\mathbf {v} \subset H$
, (6.1) implies that the i-th coordinate of
$\mathbf {v} \subset H$
, (6.1) implies that the i-th coordinate of
![]() $v^{(i+1)} - v^{(i)}$
is nonpositive.
$v^{(i+1)} - v^{(i)}$
is nonpositive.
Remark 6.2. The set of
![]() $(k,n)$
-Grassmann necklaces (see Section 2) is exactly the set of Coxeter necklaces
$(k,n)$
-Grassmann necklaces (see Section 2) is exactly the set of Coxeter necklaces
![]() $\mathbf {v}= (v^{(1)},v^{(2)},\ldots ,v^{(n)})$
in
$\mathbf {v}= (v^{(1)},v^{(2)},\ldots ,v^{(n)})$
in
![]() $H_k$
, such that each
$H_k$
, such that each
![]() $v^{(i)}$
is a
$v^{(i)}$
is a
![]() $01$
-vector.
$01$
-vector.
The sum of two Coxeter necklaces
![]() $\mathbf {v} \in H_k$
and
$\mathbf {v} \in H_k$
and
![]() $\mathbf {v}'\in H_{k'}$
is a Coxeter necklace
$\mathbf {v}'\in H_{k'}$
is a Coxeter necklace
![]() $\mathbf {v}"\in H_{k+k'}$
. Recall that the polytope
$\mathbf {v}"\in H_{k+k'}$
. Recall that the polytope
![]() $Q(\mathbf {v})$
was defined in (5.2).
$Q(\mathbf {v})$
was defined in (5.2).
Lemma 6.3. The space of Coxeter necklaces for varying
![]() $H=H_k$
form a cone. The map
$H=H_k$
form a cone. The map
![]() $\mathbf {v} \to Q(\mathbf {v})$
induces a homomorphism of cones from Coxeter necklaces to
$\mathbf {v} \to Q(\mathbf {v})$
induces a homomorphism of cones from Coxeter necklaces to
![]() ${\mathcal {C}}_{\mathrm {alc}}$
.
${\mathcal {C}}_{\mathrm {alc}}$
.
It will follow from Theorem 6.12 below that the image of this homomorphism of cones is
![]() ${\mathcal {C}}_{\mathrm {pol}}$
.
${\mathcal {C}}_{\mathrm {pol}}$
.
Lemma 6.4. Suppose that
![]() $\mathbf {v}=(v^{(1)},v^{(2)},\ldots ,v^{(n)})$
is a Coxeter necklace. Then each
$\mathbf {v}=(v^{(1)},v^{(2)},\ldots ,v^{(n)})$
is a Coxeter necklace. Then each
![]() $v^{(i)}$
is a vertex of
$v^{(i)}$
is a vertex of
![]() $Q(\mathbf {v})$
.
$Q(\mathbf {v})$
.
Proof. It suffices to show that
![]() $v^{(i)} \in Q(\mathbf {v})$
. We will show that
$v^{(i)} \in Q(\mathbf {v})$
. We will show that
![]() $v^{(i)}_{[1,j]} \leq v^{(1)}_{[1,j]}$
; the full set of inequalities follows by cyclic symmetry. Suppose
$v^{(i)}_{[1,j]} \leq v^{(1)}_{[1,j]}$
; the full set of inequalities follows by cyclic symmetry. Suppose
![]() $i \leq j+1$
. Then
$i \leq j+1$
. Then
using the definition (6.1) and the fact
![]() $k-1 \in [1,j]$
. Suppose
$k-1 \in [1,j]$
. Suppose
![]() $i> j +1$
. Then
$i> j +1$
. Then
using the definition (6.1) and the fact that
![]() $k-1 \notin [1,j]$
.
$k-1 \notin [1,j]$
.
It follows from Lemma 6.4 that the map
![]() $\mathbf {v} \to Q(\mathbf {v})$
is injective.
$\mathbf {v} \to Q(\mathbf {v})$
is injective.
Proposition 6.5. Suppose P is a generalized permutohedron in H with vertices
![]() $\{v_w \mid w \in S_n\}$
. Then
$\{v_w \mid w \in S_n\}$
. Then
-
1. the sequence
 $(v_{\mathrm {id}}, v_{c}, v_{c^{2}},\ldots ,v_{c^{n-1}})$
is a Coxeter necklace,
$(v_{\mathrm {id}}, v_{c}, v_{c^{2}},\ldots ,v_{c^{n-1}})$
is a Coxeter necklace, -
2. one has
 $v_{c^{i-1}} = v^{(i)}(P)$
for
$v_{c^{i-1}} = v^{(i)}(P)$
for
 $i = 1, \ldots , n$
, where
$i = 1, \ldots , n$
, where
 $v^{(i)}$
is defined in (5.3).
$v^{(i)}$
is defined in (5.3).
Proof. For (1), we show that all but the first coordinate of
![]() $v_{c} - v_{\mathrm {id}}$
is nonnegative, and a similar argument shows that the entire sequence is a Coxeter necklace. We have
$v_{c} - v_{\mathrm {id}}$
is nonnegative, and a similar argument shows that the entire sequence is a Coxeter necklace. We have
![]() $c = 23 \cdots 1$
in one-line notation. By Theorem 3.2(3),
$c = 23 \cdots 1$
in one-line notation. By Theorem 3.2(3),
 $$ \begin{align*} v_{213 \cdots n} - v_{123\cdots n} &\in &&\mathbb{R}_{\geq 0}((-2,-1,-3,\ldots) - (-1,-2,-3,\ldots)) = \mathbb{R}_{\geq0}(e_2-e_1) \\ v_{2314 \cdots n} - v_{213\cdots n} &\in&& \mathbb{R}_{\geq 0}((-3,-1,-2,\ldots) - (-2,-1,-3,\ldots)) = \mathbb{R}_{\geq 0}(e_3-e_1) \\ \cdots \\ v_{23 \cdots (n-1) n 1}-v_{23 \cdots(n-1) 1 n} &\in &&\mathbb{R}_{\geq0}((-n,-1,-2,\ldots,1-n) - (1-n,-1,-2,\ldots,-n)) \\ &&& =\mathbb{R}_{\geq 0}(e_n-e_1). \end{align*} $$
$$ \begin{align*} v_{213 \cdots n} - v_{123\cdots n} &\in &&\mathbb{R}_{\geq 0}((-2,-1,-3,\ldots) - (-1,-2,-3,\ldots)) = \mathbb{R}_{\geq0}(e_2-e_1) \\ v_{2314 \cdots n} - v_{213\cdots n} &\in&& \mathbb{R}_{\geq 0}((-3,-1,-2,\ldots) - (-2,-1,-3,\ldots)) = \mathbb{R}_{\geq 0}(e_3-e_1) \\ \cdots \\ v_{23 \cdots (n-1) n 1}-v_{23 \cdots(n-1) 1 n} &\in &&\mathbb{R}_{\geq0}((-n,-1,-2,\ldots,1-n) - (1-n,-1,-2,\ldots,-n)) \\ &&& =\mathbb{R}_{\geq 0}(e_n-e_1). \end{align*} $$
It follows that all but the first coordinate of
![]() $v_{c} - v_{\mathrm {id}}$
is nonnegative.
$v_{c} - v_{\mathrm {id}}$
is nonnegative.
For (2), we note that all edges of P incident to
![]() $v_{c^{i-1}}$
are in the same direction as an edge of the cone
$v_{c^{i-1}}$
are in the same direction as an edge of the cone
![]() $C_{i}$
. It follows that
$C_{i}$
. It follows that
![]() $P \subset v_{c^{i-1}} + C_i$
, so that
$P \subset v_{c^{i-1}} + C_i$
, so that
![]() $v_{c^{i-1}} = v^{(i)}(P)$
.
$v_{c^{i-1}} = v^{(i)}(P)$
.
6.2. Balanced digraphs
Definition 6.6. Let G be a real-weighted directed graph on the vertex set
![]() $[n]$
. Let
$[n]$
. Let
![]() $m_{ij} \in \mathbb {R}$
denote the weight of the edge
$m_{ij} \in \mathbb {R}$
denote the weight of the edge
![]() $i \to j$
of G (we assume that
$i \to j$
of G (we assume that
![]() $m_{ij}=0$
if G does not contain the edge
$m_{ij}=0$
if G does not contain the edge
![]() $i\to j$
). We say that G is balanced if
$i\to j$
). We say that G is balanced if
-
1. the weight of nonloop edges are nonnegative, that is,
 $m_{ij} \in \mathbb {R}_{\geq 0}$
when
$m_{ij} \in \mathbb {R}_{\geq 0}$
when
 $i \neq j$
;
$i \neq j$
; -
2. the total outdegree is equal to the total indegree of each vertex; that is, for each i one has
(6.2) $$ \begin{align} \sum_{j=1}^n m_{ij} = \sum_{j =1}^n m_{ji}. \end{align} $$
$$ \begin{align} \sum_{j=1}^n m_{ij} = \sum_{j =1}^n m_{ji}. \end{align} $$
Remark 6.7. The set of decorated permutations (see Section 2) is the same as the set of balanced graphs satisfying the following two conditions: (a) every vertex has one nonzero incoming edge and one nonzero outgoing edge, and (b) all edges have weight
![]() $\pm 1$
(only loop edges can have weight
$\pm 1$
(only loop edges can have weight
![]() $-1$
).
$-1$
).
Lemma 6.8. Suppose G is a balanced digraph. Then the quantity
 $$ \begin{align*}S_i(G) := \sum_{j \in [n]} (m_{j,j} + m_{j+1,j} + \cdots + m_{i,j}) \end{align*} $$
$$ \begin{align*}S_i(G) := \sum_{j \in [n]} (m_{j,j} + m_{j+1,j} + \cdots + m_{i,j}) \end{align*} $$
does not depend on
![]() $i \in [n]$
(indices are taken modulo n in the sum
$i \in [n]$
(indices are taken modulo n in the sum
![]() $m_{j,j} + m_{j+1,j} + \cdots + m_{i,j}$
).
$m_{j,j} + m_{j+1,j} + \cdots + m_{i,j}$
).
Proof. We have
![]() $S_i - S_{i+1} = \sum _{j \in [n]} m_{j,i+1} - \sum _{j \in [n]} m_{i+1,j} = 0. $
$S_i - S_{i+1} = \sum _{j \in [n]} m_{j,i+1} - \sum _{j \in [n]} m_{i+1,j} = 0. $
For a balanced digraph G, we define
![]() $S(G) = S_i(G)$
to be the sum of Lemma 6.8.
$S(G) = S_i(G)$
to be the sum of Lemma 6.8.
Note that the space of balanced graphs forms a cone in a natural way:
![]() $G= \alpha G' + \beta G"$
has weights given by
$G= \alpha G' + \beta G"$
has weights given by
![]() $m_{ij}= \alpha m^{\prime }_{ij} + \beta m^{\prime \prime }_{ij}$
.
$m_{ij}= \alpha m^{\prime }_{ij} + \beta m^{\prime \prime }_{ij}$
.
Proposition 6.9. Every balanced graph G is a linear combination of balanced directed cycles (including loops and cycles of length
![]() $2$
), such that the coefficients of those cycles that are not loops are nonnegative.
$2$
), such that the coefficients of those cycles that are not loops are nonnegative.
Proof. Let G be a balanced graph. We may assume that
![]() $m_{ii}=0$
for all
$m_{ii}=0$
for all
![]() $i \in [n]$
. Let
$i \in [n]$
. Let
![]() $m_{ij}>0$
be minimal amongst the positive weights. Then the unweighted graph underlying G must contain a directed cycle C containing the edge
$m_{ij}>0$
be minimal amongst the positive weights. Then the unweighted graph underlying G must contain a directed cycle C containing the edge
![]() $i \to j$
. All the weights
$i \to j$
. All the weights
![]() $m_e$
for e an edge of C satisfy
$m_e$
for e an edge of C satisfy
![]() $m_e \geq m_{ij}$
. Thus, we may write
$m_e \geq m_{ij}$
. Thus, we may write
![]() $G = G' + C(m_{ij})$
, where
$G = G' + C(m_{ij})$
, where
![]() $C(m_{ij})$
is the balanced directed cycle, where all edges have weight
$C(m_{ij})$
is the balanced directed cycle, where all edges have weight
![]() $m_{ij}$
, and
$m_{ij}$
, and
![]() $G'$
is still a balanced graph. But
$G'$
is still a balanced graph. But
![]() $G'$
has fewer edges (with nonzero weight) than G, so repeating this reduction, we deduce the proposition.
$G'$
has fewer edges (with nonzero weight) than G, so repeating this reduction, we deduce the proposition.
Let
![]() $\mathbf {v} = (v^{(1)},v^{(2)},\ldots ,v^{(n)})$
be a balanced sequence of points in H. We define a weighted directed graph
$\mathbf {v} = (v^{(1)},v^{(2)},\ldots ,v^{(n)})$
be a balanced sequence of points in H. We define a weighted directed graph
![]() $G(\mathbf {v})$
by the formula
$G(\mathbf {v})$
by the formula
 $$ \begin{align} m_{ij} = \begin{cases} (v^{(i+1)}- v^{(i)})_j &\mbox{ if } j \neq i, \\ v^{(i+1)}_i & \mbox{if } j = i. \end{cases} \end{align} $$
$$ \begin{align} m_{ij} = \begin{cases} (v^{(i+1)}- v^{(i)})_j &\mbox{ if } j \neq i, \\ v^{(i+1)}_i & \mbox{if } j = i. \end{cases} \end{align} $$
Lemma 6.10. The map
![]() $\mathbf {v} \mapsto G(\mathbf {v})$
is a bijection between Coxeter necklaces in H, and balanced graphs G satisfying
$\mathbf {v} \mapsto G(\mathbf {v})$
is a bijection between Coxeter necklaces in H, and balanced graphs G satisfying
![]() $S(G) = k$
. Furthermore, allowing k to vary, we obtain an isomorphism of cones.
$S(G) = k$
. Furthermore, allowing k to vary, we obtain an isomorphism of cones.
Proof. We first check that
![]() $G(\mathbf {v})$
is a balanced graph. By definition of a balanced sequence,
$G(\mathbf {v})$
is a balanced graph. By definition of a balanced sequence,
![]() $m_{ij} \in \mathbb {R}_{\geq 0}$
. We have for each
$m_{ij} \in \mathbb {R}_{\geq 0}$
. We have for each
![]() $i \in [n]$
,
$i \in [n]$
,
 $$ \begin{align*} \sum_{j \in [n]} m_{ij} &=\sum_{j \in [n]} (v^{(i+1)} - v^{(i)})_j + v^{(i)}_i = v^{(i)}_i = \sum_{j \in [n]} (v^{(j+1)} - v^{(j)})_i + v^{(i)}_i = \sum_{j \in [n]} m_{ji}, \end{align*} $$
$$ \begin{align*} \sum_{j \in [n]} m_{ij} &=\sum_{j \in [n]} (v^{(i+1)} - v^{(i)})_j + v^{(i)}_i = v^{(i)}_i = \sum_{j \in [n]} (v^{(j+1)} - v^{(j)})_i + v^{(i)}_i = \sum_{j \in [n]} m_{ji}, \end{align*} $$
so
![]() $G(\mathbf {v})$
is balanced. Finally, using
$G(\mathbf {v})$
is balanced. Finally, using
![]() $v^{(i+1)}_j = m_{j,j}+ \cdots + m_{i,j}$
, one obtains
$v^{(i+1)}_j = m_{j,j}+ \cdots + m_{i,j}$
, one obtains
![]() $S(G) = \sum _j v^{(i+1)}_j = k$
.
$S(G) = \sum _j v^{(i+1)}_j = k$
.
Conversely, suppose we are given a balanced graph satisfying
![]() $S(G) = k$
. Then we define a sequence
$S(G) = k$
. Then we define a sequence
![]() $\mathbf {v}$
by
$\mathbf {v}$
by
![]() $v^{(i+1)}_j = m_{j,j}+ \cdots + m_{i,j}$
. It is easy to verify that
$v^{(i+1)}_j = m_{j,j}+ \cdots + m_{i,j}$
. It is easy to verify that
![]() $\mathbf {v}$
is a balanced sequence in H, and that this is inverse to
$\mathbf {v}$
is a balanced sequence in H, and that this is inverse to
![]() $\mathbf {v} \mapsto G(\mathbf {v})$
.
$\mathbf {v} \mapsto G(\mathbf {v})$
.
The last statement follows immediately from the linearity of (6.3).
We write
![]() $\mathbf {v}(G)$
for the Coxeter necklace associated to a balanced digraph G.
$\mathbf {v}(G)$
for the Coxeter necklace associated to a balanced digraph G.
Example 6.11. Let G be the balanced digraph on
![]() $[4]$
, such that
$[4]$
, such that
![]() $m_{ij} = 1$
for all
$m_{ij} = 1$
for all
![]() $i \neq j$
. Then
$i \neq j$
. Then
![]() $S(G) = 6$
and
$S(G) = 6$
and
![]() $\mathbf {v}(G)$
is given by
$\mathbf {v}(G)$
is given by
6.3. Parametrization
Theorem 6.12. There are natural bijections between the following sets:
-
1. The set of all polypositroids
 $P \subset H_k$
.
$P \subset H_k$
. -
2. The set of all Coxeter necklaces in
 $H_k$
.
$H_k$
. -
3. The set of all balanced digraphs G with
 $S(G) = k$
.
$S(G) = k$
.
Furthermore, these bijections are compatible with the respective cone structures on the three sets.
After Lemma 6.10, it suffices to show that the map
![]() $\mathbf {v} \to Q(\mathbf {v})$
is a bijection between Coxeter necklaces and polypositroids. We delay the proof of Theorem 6.12 to Section 6.5.
$\mathbf {v} \to Q(\mathbf {v})$
is a bijection between Coxeter necklaces and polypositroids. We delay the proof of Theorem 6.12 to Section 6.5.
The following result follows easily from the definition of the cone of balanced digraphs.
Corollary 6.13. The cone of balanced digraphs G satisfying
![]() $S(G) = 0$
has
$S(G) = 0$
has
![]() $n(n-1)$
facets, given by the inequalities
$n(n-1)$
facets, given by the inequalities
![]() $m_{ij} \geq 0$
for
$m_{ij} \geq 0$
for
![]() $i \neq j$
. Thus, the cone
$i \neq j$
. Thus, the cone
![]() ${\mathcal {C}}_{\mathrm {pol}}$
also has
${\mathcal {C}}_{\mathrm {pol}}$
also has
![]() $n(n-1)$
facets.
$n(n-1)$
facets.
The group
![]() $H_0=\mathbb {R}^{n-1}$
of translations preserves the affine hyperplane
$H_0=\mathbb {R}^{n-1}$
of translations preserves the affine hyperplane
![]() $H_k$
and acts on the cone
$H_k$
and acts on the cone
![]() ${\mathcal {C}}_{\mathrm {pol}}$
of polypositroids via the formula
${\mathcal {C}}_{\mathrm {pol}}$
of polypositroids via the formula
![]() $z: (a_{ij}) \mapsto (a_{ij} + (h_i-h_j)(z))$
, where
$z: (a_{ij}) \mapsto (a_{ij} + (h_i-h_j)(z))$
, where
![]() $z = (z_1,z_2,\ldots ,z_n) \in H_0$
. The lineality space of the cone
$z = (z_1,z_2,\ldots ,z_n) \in H_0$
. The lineality space of the cone
![]() ${\mathcal {C}}_{\mathrm {pol}}$
can be identified with
${\mathcal {C}}_{\mathrm {pol}}$
can be identified with
![]() $\mathbb {R}^{n-1}$
. Let
$\mathbb {R}^{n-1}$
. Let
![]() ${\mathcal {C}}_{\mathrm {pol}}' := {\mathcal {C}}_{\mathrm { pol}}/\mathbb {R}^{n-1}$
denote the quotient cone, which may be identified with the set of polypositroids inside
${\mathcal {C}}_{\mathrm {pol}}' := {\mathcal {C}}_{\mathrm { pol}}/\mathbb {R}^{n-1}$
denote the quotient cone, which may be identified with the set of polypositroids inside
![]() $H_0$
, modulo translations.
$H_0$
, modulo translations.
Corollary 6.14. The cone
![]() ${\mathcal {C}}_{\mathrm {pol}}'$
is a pointed cone, with extremal rays corresponding to the polypositroids
${\mathcal {C}}_{\mathrm {pol}}'$
is a pointed cone, with extremal rays corresponding to the polypositroids
![]() $Q(\mathbf {v}(G))$
, where G is a balanced directed cycle (including cycles of length
$Q(\mathbf {v}(G))$
, where G is a balanced directed cycle (including cycles of length
![]() $2$
).
$2$
).
Proof. By Theorem 6.12, we are equivalently considering the cone of balanced digraphs with
![]() $S(G) = 0$
. The translation action of
$S(G) = 0$
. The translation action of
![]() $\mathbb {R}^{n-1}$
on
$\mathbb {R}^{n-1}$
on
![]() $H_0$
corresponds to changing the weight of the n loop edges of G. Ignoring the weights of the loops, the statement then follows from Proposition 6.9.
$H_0$
corresponds to changing the weight of the n loop edges of G. Ignoring the weights of the loops, the statement then follows from Proposition 6.9.
6.4. Face graphs
Let P be an alcoved polytope and F a face of P. We define the graph
![]() $T_F$
of P at F to be the directed graph on
$T_F$
of P at F to be the directed graph on
![]() $[n]$
with a directed edge
$[n]$
with a directed edge
![]() $(i \to j)$
whenever F lies on the hyperplane
$(i \to j)$
whenever F lies on the hyperplane
![]() $(h_j- h_i)(x) \leq a_{ji}$
, or equivalently, on the hyperplane
$(h_j- h_i)(x) \leq a_{ji}$
, or equivalently, on the hyperplane
![]() $x_{[i+1,j]} = f_{[i+1,j]}$
. We say that a digraph T on
$x_{[i+1,j]} = f_{[i+1,j]}$
. We say that a digraph T on
![]() $[n]$
is noncrossing if, when the graph is drawn inside a circle with the vertices
$[n]$
is noncrossing if, when the graph is drawn inside a circle with the vertices
![]() $[n]$
arranged in clockwise order, there are no intersections in the interior of the circle. We say that a digraph T on
$[n]$
arranged in clockwise order, there are no intersections in the interior of the circle. We say that a digraph T on
![]() $[n]$
is alternating if no vertex has both incoming and outgoing edges.
$[n]$
is alternating if no vertex has both incoming and outgoing edges.
Lemma 6.15. Suppose E is an edge of an alcoved polytope P, with a noncrossing graph
![]() $T_E$
. Then E is parallel to
$T_E$
. Then E is parallel to
![]() $e_i - e_j$
for some i and j.
$e_i - e_j$
for some i and j.
Proof. Let us take a minimal subgraph
![]() $T \subset T_E$
, such that the corresponding
$T \subset T_E$
, such that the corresponding
![]() $(n-2)$
facets still define (the affine span of) E. We claim that T is a forest with two components. It is enough to show that the underlying undirected graph of T has no cycles. A cycle in T would correspond to a linear dependence in the equations defining E, contradicting the minimality of T. For the remainder of the proof, it is enough to think of T as an undirected forest.
$(n-2)$
facets still define (the affine span of) E. We claim that T is a forest with two components. It is enough to show that the underlying undirected graph of T has no cycles. A cycle in T would correspond to a linear dependence in the equations defining E, contradicting the minimality of T. For the remainder of the proof, it is enough to think of T as an undirected forest.
Let the two components of T be
![]() $T_1$
and
$T_1$
and
![]() $T_2$
. By the noncrossing assumption, it is clear that
$T_2$
. By the noncrossing assumption, it is clear that
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are induced subgraphs of T on cyclic intervals
$T_2$
are induced subgraphs of T on cyclic intervals
![]() $[i,j-1]$
and
$[i,j-1]$
and
![]() $[j,i-1]$
.
$[j,i-1]$
.
Let
![]() $x = (x_1,\ldots ,x_n)$
lie on E. We claim that if
$x = (x_1,\ldots ,x_n)$
lie on E. We claim that if
![]() $k \notin \{i, j\}$
, then
$k \notin \{i, j\}$
, then
![]() $x_k$
is fixed (that is, constant on E). For simplicity, we shall assume that
$x_k$
is fixed (that is, constant on E). For simplicity, we shall assume that
![]() $x_k$
lies in a component
$x_k$
lies in a component
![]() $T_1$
of T which is an induced subgraph on a usual interval (no wraparound). First, note that an edge of the form
$T_1$
of T which is an induced subgraph on a usual interval (no wraparound). First, note that an edge of the form
![]() $(r, r+1) \in T_1$
completely determines
$(r, r+1) \in T_1$
completely determines
![]() $x_{r+1}$
. Also, if
$x_{r+1}$
. Also, if
![]() $(r, s) \in T$
is an edge, and all but one of the coordinates
$(r, s) \in T$
is an edge, and all but one of the coordinates
![]() $\{x_{r+1}, x_{r+2}, \ldots , x_{s}\}$
is determined, then the last coordinate is also determined. By induction on the length of edges, we thus see that for each edge
$\{x_{r+1}, x_{r+2}, \ldots , x_{s}\}$
is determined, then the last coordinate is also determined. By induction on the length of edges, we thus see that for each edge
![]() $(r,s) \in T_1$
, all of
$(r,s) \in T_1$
, all of
![]() $\{x_{r+1}, x_{r+2}, \ldots , x_{s}\}$
are determined, proving our claim that
$\{x_{r+1}, x_{r+2}, \ldots , x_{s}\}$
are determined, proving our claim that
![]() $x_k$
is fixed for
$x_k$
is fixed for
![]() $k \notin \{i,j\}$
.
$k \notin \{i,j\}$
.
Thus, only the coordinates
![]() $x_i$
and
$x_i$
and
![]() $x_j$
vary on E. Since
$x_j$
vary on E. Since
![]() $E \in H$
, we deduce that E is parallel to
$E \in H$
, we deduce that E is parallel to
![]() $e_i - e_j$
.
$e_i - e_j$
.
Remark 6.16. The converse of Lemma 6.15 is false. For example, consider an alcoved polytope P in
![]() $H = \{x \in \mathbb {R}^5 \mid x_1 + x_2 + \cdots + x_5 = 0\}$
, where
$H = \{x \in \mathbb {R}^5 \mid x_1 + x_2 + \cdots + x_5 = 0\}$
, where
![]() $x_2 \leq 0$
,
$x_2 \leq 0$
,
![]() $x_2 + x_3 \leq 0$
, and
$x_2 + x_3 \leq 0$
, and
![]() $x_3+x_4 \geq 0$
are all facets, and so that
$x_3+x_4 \geq 0$
are all facets, and so that
![]() $x_2 = x_2+x_3 = x_3+x_4 = 0$
defines an edge E of P. Then
$x_2 = x_2+x_3 = x_3+x_4 = 0$
defines an edge E of P. Then
![]() $T_E$
contains the directed edges
$T_E$
contains the directed edges
![]() $(1 \to 2), (1 \to 3), (2 \to 4)$
and is alternating but not noncrossing. However, the edge E is clearly in the direction
$(1 \to 2), (1 \to 3), (2 \to 4)$
and is alternating but not noncrossing. However, the edge E is clearly in the direction
![]() $e_1 - e_5$
.
$e_1 - e_5$
.
Let us say that a Coxeter necklace
![]() $(v^{(1)},\ldots ,v^{(n)})$
is generic if every coordinate of
$(v^{(1)},\ldots ,v^{(n)})$
is generic if every coordinate of
![]() $v^{(i+1)} - v^{(i)}$
is nonzero, for every i. This is equivalent to saying that all the nonloop edges of the graph
$v^{(i+1)} - v^{(i)}$
is nonzero, for every i. This is equivalent to saying that all the nonloop edges of the graph
![]() $G(\mathbf {v})$
are nonzero.
$G(\mathbf {v})$
are nonzero.
Lemma 6.17. Let
![]() $(v^{(1)},\ldots ,v^{(n)})$
be a generic Coxeter necklace in H. Then any face F of the alcoved polytope
$(v^{(1)},\ldots ,v^{(n)})$
be a generic Coxeter necklace in H. Then any face F of the alcoved polytope
![]() $Q = \bigcap _{i\in \mathbb {Z}/n\mathbb {Z}} (v^{(i)} + C_{i})$
has a noncrossing and alternating graph
$Q = \bigcap _{i\in \mathbb {Z}/n\mathbb {Z}} (v^{(i)} + C_{i})$
has a noncrossing and alternating graph
![]() $T_F$
.
$T_F$
.
Proof. Let F be a face, such that
![]() $T_F$
is either not noncrossing or not alternating.
$T_F$
is either not noncrossing or not alternating.
Suppose
![]() $[r,s]$
and
$[r,s]$
and
![]() $[r',s']$
are cyclic intervals so that the corresponding directed edges
$[r',s']$
are cyclic intervals so that the corresponding directed edges
![]() $(r-1) \to s$
and
$(r-1) \to s$
and
![]() $(r'-1) \to s'$
in
$(r'-1) \to s'$
in
![]() $T_F$
are either crossing or form a directed path
$T_F$
are either crossing or form a directed path
![]() $(r-1) \to s = (r'-1) \to s'$
. In the crossing case, we may assume that
$(r-1) \to s = (r'-1) \to s'$
. In the crossing case, we may assume that
![]() $r < r' \leq s < s'< r$
(interpreted in a cyclic manner). We have the following equations and inequalities
$r < r' \leq s < s'< r$
(interpreted in a cyclic manner). We have the following equations and inequalities
for points
![]() $x = (x_1,x_2,\ldots ,x_n)$
on the face F. By (6.4) and (6.7), we have
$x = (x_1,x_2,\ldots ,x_n)$
on the face F. By (6.4) and (6.7), we have
and by (6.5) and (6.6), we have
Equating the two expressions for
![]() $x_{[r,r'-1]}$
, we obtain
$x_{[r,r'-1]}$
, we obtain
This is impossible because
![]() $\mathbf {v}$
is generic balanced, implying that the coordinates in the positions
$\mathbf {v}$
is generic balanced, implying that the coordinates in the positions
![]() $[s+1,s']$
of
$[s+1,s']$
of
![]() $v^{(r')}- v^{(r)}$
are all positive.
$v^{(r')}- v^{(r)}$
are all positive.
6.5. Proof of Theorem 6.12
Let
![]() $\mathbf {v} = (v^{(1)},\ldots ,v^{(n)})$
be a Coxeter necklace in H. We show that
$\mathbf {v} = (v^{(1)},\ldots ,v^{(n)})$
be a Coxeter necklace in H. We show that
![]() $Q(\mathbf {v})$
is a polypositroid. First, suppose that
$Q(\mathbf {v})$
is a polypositroid. First, suppose that
![]() $\mathbf {v}$
is generic. Then by Lemmas 6.15 and 6.17,
$\mathbf {v}$
is generic. Then by Lemmas 6.15 and 6.17,
![]() $Q(\mathbf {v})$
is a generalized permutohedron, and thus a polypositroid.
$Q(\mathbf {v})$
is a generalized permutohedron, and thus a polypositroid.
Now suppose that
![]() $\mathbf {v}$
is not generic, and let
$\mathbf {v}$
is not generic, and let
![]() $G(\mathbf {v})$
be the balanced digraph under the bijection of Lemma 6.10. Let
$G(\mathbf {v})$
be the balanced digraph under the bijection of Lemma 6.10. Let
![]() $G_{\varepsilon }$
be obtained from
$G_{\varepsilon }$
be obtained from
![]() $G(\mathbf {v})$
by adding
$G(\mathbf {v})$
by adding
![]() $\varepsilon>0$
to every nonloop edge. It is immediate that
$\varepsilon>0$
to every nonloop edge. It is immediate that
![]() $G(\varepsilon )$
is again a balanced digraph, and we define the Coxeter necklace
$G(\varepsilon )$
is again a balanced digraph, and we define the Coxeter necklace
![]() $\mathbf {v}_{\varepsilon }$
by
$\mathbf {v}_{\varepsilon }$
by
![]() $G(\mathbf {v}_{\varepsilon }) = G_{\varepsilon }$
. Then
$G(\mathbf {v}_{\varepsilon }) = G_{\varepsilon }$
. Then
![]() $\mathbf {v} = \lim _{\varepsilon \to 0} \mathbf {v}_{\varepsilon }$
is a limit of the generic balanced sequences
$\mathbf {v} = \lim _{\varepsilon \to 0} \mathbf {v}_{\varepsilon }$
is a limit of the generic balanced sequences
![]() $\mathbf {v}_{\varepsilon }$
. For sufficiently small but nonzero
$\mathbf {v}_{\varepsilon }$
. For sufficiently small but nonzero
![]() $\varepsilon $
, the combinatorial type of the polytope
$\varepsilon $
, the combinatorial type of the polytope
![]() $Q(\mathbf {v}_{\varepsilon })$
corresponding to
$Q(\mathbf {v}_{\varepsilon })$
corresponding to
![]() $\mathbf {v}_{\varepsilon }$
does not change. The alcoved polytope Q is thus a deformation of such a
$\mathbf {v}_{\varepsilon }$
does not change. The alcoved polytope Q is thus a deformation of such a
![]() $Q(\mathbf {v}_{\varepsilon })$
, in the sense of moving facets. Since
$Q(\mathbf {v}_{\varepsilon })$
, in the sense of moving facets. Since
![]() $Q(\mathbf {v}_{\varepsilon })$
is a generalized permutohedron, so is
$Q(\mathbf {v}_{\varepsilon })$
is a generalized permutohedron, so is
![]() $Q(\mathbf {v})$
(see, for example [Reference Castillo and LiuCL]).
$Q(\mathbf {v})$
(see, for example [Reference Castillo and LiuCL]).
Now suppose P is a polypositroid with vertices
![]() $v_w$
. Since P is a generalized permutohedron, by Proposition 6.5 and Lemma 5.1,
$v_w$
. Since P is a generalized permutohedron, by Proposition 6.5 and Lemma 5.1,
![]() $\mathbf {v} = (v_{\mathrm {id}}, v_{c}, v_{c^{2}},\ldots ,v_{c^{n-1}})$
is balanced, and we have
$\mathbf {v} = (v_{\mathrm {id}}, v_{c}, v_{c^{2}},\ldots ,v_{c^{n-1}})$
is balanced, and we have
![]() $\mathrm {env}(P) = Q(\mathbf {v})$
. But P is also alcoved, so we have
$\mathrm {env}(P) = Q(\mathbf {v})$
. But P is also alcoved, so we have
![]() $P = \mathrm {env}(P) = Q(\mathbf {v})$
. Thus, the map
$P = \mathrm {env}(P) = Q(\mathbf {v})$
. Thus, the map
![]() $\mathbf {v} \mapsto Q(\mathbf {v})$
is surjective. Finally, it follows from Lemma 6.4 that
$\mathbf {v} \mapsto Q(\mathbf {v})$
is surjective. Finally, it follows from Lemma 6.4 that
![]() $\mathbf {v} \mapsto Q(\mathbf {v})$
is injective. This proves the equivalence of (1) and (2) in Theorem 6.12.
$\mathbf {v} \mapsto Q(\mathbf {v})$
is injective. This proves the equivalence of (1) and (2) in Theorem 6.12.
6.6. Proof of Theorem 4.8
The following result follows immediately from Proposition 6.5(1) and Theorem 6.12.
Proposition 6.18. The alcoved envelope of a generalized permutohedron is a generalized permutohedron, and thus a polypositroid.
Recall that
![]() $\pi _{\mathcal {I}}$
denotes the composition of the restriction map
$\pi _{\mathcal {I}}$
denotes the composition of the restriction map
![]() $f_P \mapsto f_P|_{\mathcal {I}}$
with the transformation (3.4) from
$f_P \mapsto f_P|_{\mathcal {I}}$
with the transformation (3.4) from
![]() $f_{[r,s]}$
-coordinates to
$f_{[r,s]}$
-coordinates to
![]() $a_{ij}$
coordinates. Let P be a generalized permutohedron and
$a_{ij}$
coordinates. Let P be a generalized permutohedron and
![]() $f_P|_{2^{[n]}} \in {\mathcal {C}}_{\mathrm {sub}}$
be its support function. Then
$f_P|_{2^{[n]}} \in {\mathcal {C}}_{\mathrm {sub}}$
be its support function. Then
![]() $\pi _{\mathcal {I}}(f_P)$
represents the alcoved polytope
$\pi _{\mathcal {I}}(f_P)$
represents the alcoved polytope
![]() $\mathrm {env}(P)$
. By Proposition 6.18, we thus have
$\mathrm {env}(P)$
. By Proposition 6.18, we thus have
![]() $\pi _I({\mathcal {C}}_{\mathrm {sub}}) \subseteq {\mathcal {C}}_{\mathrm { pol}}$
. But if P is a polypositroid, then
$\pi _I({\mathcal {C}}_{\mathrm {sub}}) \subseteq {\mathcal {C}}_{\mathrm { pol}}$
. But if P is a polypositroid, then
![]() $\mathrm {env}(P) = P$
. It follows that
$\mathrm {env}(P) = P$
. It follows that
![]() $\pi _{\mathcal {I}}({\mathcal {C}}_{\mathrm {sub}}) = {\mathcal {C}}_{\mathrm {pol}}$
.
$\pi _{\mathcal {I}}({\mathcal {C}}_{\mathrm {sub}}) = {\mathcal {C}}_{\mathrm {pol}}$
.
7. Components of a polypositroid
A noncrossing partition
![]() $\tau = (\tau _1|\tau _2|\cdots |\tau _{\ell })$
of
$\tau = (\tau _1|\tau _2|\cdots |\tau _{\ell })$
of
![]() $[n]$
is a partition of
$[n]$
is a partition of
![]() $[n]$
, such that there do not exist
$[n]$
, such that there do not exist
![]() $1 \leq i < j < k <l \leq n$
, such that
$1 \leq i < j < k <l \leq n$
, such that
![]() $i,k \in \tau _a$
and
$i,k \in \tau _a$
and
![]() $j,l \in \tau _b$
for
$j,l \in \tau _b$
for
![]() $a \neq b$
. Let G be a graph on
$a \neq b$
. Let G be a graph on
![]() $[n]$
. Then there exists a finest noncrossing partition
$[n]$
. Then there exists a finest noncrossing partition
![]() $\tau (G)= (\tau _1|\tau _2|\cdots |\tau _{\ell })$
of
$\tau (G)= (\tau _1|\tau _2|\cdots |\tau _{\ell })$
of
![]() $[n]$
, such that G is the disjoint union of the induced subgraphs
$[n]$
, such that G is the disjoint union of the induced subgraphs
![]() $G|_{\tau _a}$
,
$G|_{\tau _a}$
,
![]() $a = 1,2,\ldots ,\ell $
. Note that the graphs
$a = 1,2,\ldots ,\ell $
. Note that the graphs
![]() $G|_{\tau _a}$
need not be connected.
$G|_{\tau _a}$
need not be connected.
If
![]() $x = (x_1,x_2,\ldots ,x_n) \in \mathbb {R}^n$
, then
$x = (x_1,x_2,\ldots ,x_n) \in \mathbb {R}^n$
, then
![]() $x|_{\tau _a} \in \mathbb {R}^{\tau _a}$
denotes the vector obtained by projecting x to the components indexed by
$x|_{\tau _a} \in \mathbb {R}^{\tau _a}$
denotes the vector obtained by projecting x to the components indexed by
![]() $\tau _a$
. Given
$\tau _a$
. Given
![]() $\mathbf {v} = (v^{(1)},\ldots ,v^{(n)})$
and
$\mathbf {v} = (v^{(1)},\ldots ,v^{(n)})$
and
![]() $\tau _a = \{i_1,i_2,\ldots ,i_t\}$
, we define
$\tau _a = \{i_1,i_2,\ldots ,i_t\}$
, we define
The following result should be compared to [Reference Ardila, Rincón and WilliamsARW16, Theorem 7.6] in the positroid case.
Lemma 7.1. Let
![]() $\mathbf {v}$
be a Coxeter necklace, and let
$\mathbf {v}$
be a Coxeter necklace, and let
![]() $\tau (G(\mathbf {v}))= (\tau _1|\tau _2|\cdots |\tau _{\ell })$
. Then
$\tau (G(\mathbf {v}))= (\tau _1|\tau _2|\cdots |\tau _{\ell })$
. Then
![]() $\mathbf {v}|_{\tau _a}$
,
$\mathbf {v}|_{\tau _a}$
,
![]() $a =1,2,\ldots , k$
are Coxeter necklaces satisfying
$a =1,2,\ldots , k$
are Coxeter necklaces satisfying
![]() $G(\mathbf {v}|_{\tau _a}) = G|_{\tau _a}$
, and we have
$G(\mathbf {v}|_{\tau _a}) = G|_{\tau _a}$
, and we have
where
![]() $Q(\mathbf {v}|_{\tau _a})$
lies inside
$Q(\mathbf {v}|_{\tau _a})$
lies inside
![]() $\mathbb {R}^{\tau _a}$
.
$\mathbb {R}^{\tau _a}$
.
Proof. The lemma holds more generally for
![]() $\tau $
any noncrossing partition, such that G is the disjoint union of the induced subgraphs
$\tau $
any noncrossing partition, such that G is the disjoint union of the induced subgraphs
![]() $G|_{\tau _a}$
, that is,
$G|_{\tau _a}$
, that is,
![]() $\tau $
need not be chosen finest. The sums
$\tau $
need not be chosen finest. The sums
![]() $k_a:= v^{(j)}_{\tau _a} = \sum _{i \in \tau _a} v^{(j)}_i$
(not to be confused with the projection
$k_a:= v^{(j)}_{\tau _a} = \sum _{i \in \tau _a} v^{(j)}_i$
(not to be confused with the projection
![]() $v^{(j)}|_{\tau _a}$
) do not depend on
$v^{(j)}|_{\tau _a}$
) do not depend on
![]() $j \in [n]$
. It follows that
$j \in [n]$
. It follows that
![]() $Q(\mathbf {v})$
lies in the hyperplane
$Q(\mathbf {v})$
lies in the hyperplane
![]() $\sum _{i \in \tau _a} x_i= k_a$
, and
$\sum _{i \in \tau _a} x_i= k_a$
, and
![]() $Q(\mathbf {v}_{\tau _a})$
lies in the same hyperplane intersected with
$Q(\mathbf {v}_{\tau _a})$
lies in the same hyperplane intersected with
![]() $\mathbb {R}^{\tau _a}$
.
$\mathbb {R}^{\tau _a}$
.
The first statement of the lemma is straightforward. For the second statement, we may assume by induction that
![]() $\tau = (\tau _1|\tau _2)$
, where
$\tau = (\tau _1|\tau _2)$
, where
![]() $\tau _a$
are cyclic intervals. The polytope
$\tau _a$
are cyclic intervals. The polytope
![]() $Q(\mathbf {v})$
is cut out by the inequalities
$Q(\mathbf {v})$
is cut out by the inequalities
![]() $x_{[r,s]} \leq v^{(r)}_{[r,s]}$
. Suppose that
$x_{[r,s]} \leq v^{(r)}_{[r,s]}$
. Suppose that
![]() $[r,s] \cap \tau _1$
and
$[r,s] \cap \tau _1$
and
![]() $[r,s] \cap \tau _2$
are both nonempty. For simplicity, we suppose that
$[r,s] \cap \tau _2$
are both nonempty. For simplicity, we suppose that
![]() $[r,s] \cap \tau _1 = [r,t]$
and
$[r,s] \cap \tau _1 = [r,t]$
and
![]() $[r,s] \cap \tau _2 = [t+1,s]$
. The assumption that there are no edges in
$[r,s] \cap \tau _2 = [t+1,s]$
. The assumption that there are no edges in
![]() $G(\mathbf {v})$
between
$G(\mathbf {v})$
between
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
implies that
$\tau _2$
implies that
![]() $v^{(r)}|_{[t+1,s]}= v^{(t+1)}|_{[t+1,s]}$
. Thus,
$v^{(r)}|_{[t+1,s]}= v^{(t+1)}|_{[t+1,s]}$
. Thus,
![]() $v^{(r)}_{[r,s]} = v^{(r)}_{[r,t]} + v^{(t+1)}|_{[t+1,s]}$
. It follows that the inequality
$v^{(r)}_{[r,s]} = v^{(r)}_{[r,t]} + v^{(t+1)}|_{[t+1,s]}$
. It follows that the inequality
![]() $x_{[r,s]} \leq v^{(r)}_{[r,s]}$
is implied by the inequalities
$x_{[r,s]} \leq v^{(r)}_{[r,s]}$
is implied by the inequalities
![]() $x_{[r,t]} \leq v^{(r)}_{[r,t]} $
and
$x_{[r,t]} \leq v^{(r)}_{[r,t]} $
and
![]() $x_{[t+1,s]} \leq v^{(t+1)}|_{[t+1,s]}$
. The latter inequalities are among those cutting out
$x_{[t+1,s]} \leq v^{(t+1)}|_{[t+1,s]}$
. The latter inequalities are among those cutting out
![]() $Q(\mathbf {v}_{\tau _1})$
and
$Q(\mathbf {v}_{\tau _1})$
and
![]() $Q(\mathbf {v}_{\tau _2})$
, respectively. It follows that
$Q(\mathbf {v}_{\tau _2})$
, respectively. It follows that
![]() $Q(\mathbf {v}) = Q(\mathbf {v}_{\tau _1}) \times Q(\mathbf {v}_{\tau _2})$
.
$Q(\mathbf {v}) = Q(\mathbf {v}_{\tau _1}) \times Q(\mathbf {v}_{\tau _2})$
.
Proposition 7.2. Let
![]() $\mathbf {v}$
be a Coxeter necklace. The dimension of the polypositroid
$\mathbf {v}$
be a Coxeter necklace. The dimension of the polypositroid
![]() $Q(\mathbf {v})$
is equal to
$Q(\mathbf {v})$
is equal to
![]() $n - \#\{\text {parts in } \tau (G)\}$
.
$n - \#\{\text {parts in } \tau (G)\}$
.
Proof. By induction and Lemma 7.1, it suffices to show
![]() $\dim (Q(\mathbf {v})) = n-1$
whenever
$\dim (Q(\mathbf {v})) = n-1$
whenever
![]() $\tau (G)=([n])$
has a single part.
$\tau (G)=([n])$
has a single part.
Assume that
![]() $\tau (G) = ([n])$
and that
$\tau (G) = ([n])$
and that
![]() $Q(\mathbf {v})$
has dimension less than
$Q(\mathbf {v})$
has dimension less than
![]() $n-1$
. Then since
$n-1$
. Then since
![]() $Q(\mathbf {v})$
is alcoved, it must lie in some hyperplane
$Q(\mathbf {v})$
is alcoved, it must lie in some hyperplane
![]() $(h_i - h_j)(x) = a_{ij}$
. This implies that
$(h_i - h_j)(x) = a_{ij}$
. This implies that
![]() $v^{(j+1)}_{[j+1,i]} = a_{ij} = v^{(i+1)}_{[j+1,i]}$
. But
$v^{(j+1)}_{[j+1,i]} = a_{ij} = v^{(i+1)}_{[j+1,i]}$
. But
 $$ \begin{align*}(v^{(i+1)}-v^{(j+1)})_{[j+1,i]} = \sum_{k \in [j+2,i+1]} (v^{(k)}-v^{(k-1)})_{[j+1,i]} \leq 0 \end{align*} $$
$$ \begin{align*}(v^{(i+1)}-v^{(j+1)})_{[j+1,i]} = \sum_{k \in [j+2,i+1]} (v^{(k)}-v^{(k-1)})_{[j+1,i]} \leq 0 \end{align*} $$
with equality if and only if there are no edges in
![]() $G(\mathbf {v})$
from the vertices
$G(\mathbf {v})$
from the vertices
![]() $[j+1,i]$
to
$[j+1,i]$
to
![]() $[i+1,j]$
. The same argument shows that there are no edges from
$[i+1,j]$
. The same argument shows that there are no edges from
![]() $[i+1,j]$
to
$[i+1,j]$
to
![]() $[j+1,i]$
, so
$[j+1,i]$
, so
![]() $\tau (G)$
must be a refinement of the partition
$\tau (G)$
must be a refinement of the partition
![]() $\tau = ([i+1,j]|[j+1,i])$
, contradicting our assumption.
$\tau = ([i+1,j]|[j+1,i])$
, contradicting our assumption.
8. Normal fans of polypositroids
8.1. Normal fans to generic simple alcoved polytopes
Recall that we say that an alcoved polytope is generic if every inequality
![]() $(h_i-h_j)(x) \leq a_{ij}$
determines a facet. The f-vector
$(h_i-h_j)(x) \leq a_{ij}$
determines a facet. The f-vector
![]() $(f_0,f_1,\ldots ,f_{d})$
of a d-dimensional polytope P is given by
$(f_0,f_1,\ldots ,f_{d})$
of a d-dimensional polytope P is given by
Theorem 8.1. The f-vectors of any two generic simple alcoved polytopes
![]() $P\subset \mathbb {R}^n$
are the same. The face numbers are given by
$P\subset \mathbb {R}^n$
are the same. The face numbers are given by
 $$ \begin{align} f_{i}= \binom{n-1}{i} \binom{2n-i-2}{n-1} \qquad \mbox{ for } i=0,1,\dots,n-1. \end{align} $$
$$ \begin{align} f_{i}= \binom{n-1}{i} \binom{2n-i-2}{n-1} \qquad \mbox{ for } i=0,1,\dots,n-1. \end{align} $$
The root polytope R is the convex hull of the vectors
![]() $\{ h_i - h_j \mid i, j \in \{1,2,\ldots ,n\}\}$
, which we think of as lying inside
$\{ h_i - h_j \mid i, j \in \{1,2,\ldots ,n\}\}$
, which we think of as lying inside
![]() $(\mathbb {R}^n)^*/h_n$
. If T is a directed tree on
$(\mathbb {R}^n)^*/h_n$
. If T is a directed tree on
![]() $[n]$
(or, more generally, a directed graph on
$[n]$
(or, more generally, a directed graph on
![]() $[n]$
), we let
$[n]$
), we let
![]() $\Delta _T \subset (\mathbb {R}^n)^*$
denote the convex hull of the points
$\Delta _T \subset (\mathbb {R}^n)^*$
denote the convex hull of the points
![]() $\{h_i - h_j \mid j \to i \; \text {is an edge of } T\} \cup \{0\}$
. A local triangulation of R is a triangulation, such that every simplex is one of the
$\{h_i - h_j \mid j \to i \; \text {is an edge of } T\} \cup \{0\}$
. A local triangulation of R is a triangulation, such that every simplex is one of the
![]() $\Delta _T$
.
$\Delta _T$
.
Let P be a generic simple alcoved polytope. The normal fan
![]() ${\mathcal F}_P$
of P lies in
${\mathcal F}_P$
of P lies in
![]() $(\mathbb {R}^n)^*/h_n$
. The condition that P is generic implies that every root
$(\mathbb {R}^n)^*/h_n$
. The condition that P is generic implies that every root
![]() $h_i - h_j \neq 0$
is an edge of
$h_i - h_j \neq 0$
is an edge of
![]() ${\mathcal F}_P$
. The condition that P is simple implies that each maximal cone
${\mathcal F}_P$
. The condition that P is simple implies that each maximal cone
![]() $C_v$
of P is spanned by
$C_v$
of P is spanned by
![]() $(n-1)$
roots. Thus, the collection of maximal cones of
$(n-1)$
roots. Thus, the collection of maximal cones of
![]() ${\mathcal F}_P$
induces a local triangulation of P. Let
${\mathcal F}_P$
induces a local triangulation of P. Let
![]() $C_T := \mathrm {span}_{\geq 0} \Delta _T$
be the cone spanned by
$C_T := \mathrm {span}_{\geq 0} \Delta _T$
be the cone spanned by
![]() $\Delta _T$
.
$\Delta _T$
.
Proof of Theorem 8.1
The f-vector of P is given by counting the number of cones of each dimension of
![]() ${\mathcal F}_P$
, which is the same as counting the number of simplices (with the origin as a vertex) of each dimension in the corresponding local triangulation of the root polytope R.
${\mathcal F}_P$
, which is the same as counting the number of simplices (with the origin as a vertex) of each dimension in the corresponding local triangulation of the root polytope R.
We claim that every local triangulation of R has the same number of simplices of each dimension. To see this, we note that since the type A root system is unimodular, every simplex
![]() $\Delta _T$
has the same volume (in fact, normalized volume 1). The number
$\Delta _T$
has the same volume (in fact, normalized volume 1). The number
![]() $\#\{\mathrm {Int}(m\Delta ) \cap \mathbb {Z}^r\}$
of integer points lying in the interior of an integer scalar multiple of a normalized volume 1 simplex
$\#\{\mathrm {Int}(m\Delta ) \cap \mathbb {Z}^r\}$
of integer points lying in the interior of an integer scalar multiple of a normalized volume 1 simplex
![]() $\Delta $
with integer coordinates depends only on the scalar multiple m and the dimension
$\Delta $
with integer coordinates depends only on the scalar multiple m and the dimension
![]() $\dim (\Delta )$
of the simplex.
$\dim (\Delta )$
of the simplex.
It follows easily from this that the Ehrhart polynomial of R can be written in terms of, and in fact determines, the number of simplices (with the origin as a vertex) in each dimension of a local triangulation. But clearly, the Ehrhart polynomial of R does not depend on the triangulation of R.
The cyclohedron (defined in (3.5)) is a generic and simple polypositroid. Thus, every generic simple polypositroid has the same f-vector as the cyclohedron. According to [Reference SimionSim], the f-vector of the cyclohedron is given by (8.1). For example, the
![]() $2$
-dimensional cyclohedron is a hexagon with face numbers
$2$
-dimensional cyclohedron is a hexagon with face numbers
![]() $(f_0,f_1,f_2) = (6,6,1)$
.
$(f_0,f_1,f_2) = (6,6,1)$
.
8.2. Matching ensembles
Let P be a generic simple alcoved polytope. Recall that in Section 6.4, we have defined the graph
![]() $T_F$
for any face F of P. When
$T_F$
for any face F of P. When
![]() $F=v$
is a vertex of P, the graph
$F=v$
is a vertex of P, the graph
![]() $T_v$
is a tree that we call a vertex tree. Let
$T_v$
is a tree that we call a vertex tree. Let
![]() ${\mathcal {T}}(P)$
denote the set of vertex trees of P. The data of
${\mathcal {T}}(P)$
denote the set of vertex trees of P. The data of
![]() ${\mathcal {T}}(P)$
are equivalent to the knowledge of the normal fan
${\mathcal {T}}(P)$
are equivalent to the knowledge of the normal fan
![]() ${\mathcal F}_P$
. Thus, the fan
${\mathcal F}_P$
. Thus, the fan
![]() ${\mathcal F}_P$
is complete, and the maximal cones
${\mathcal F}_P$
is complete, and the maximal cones
![]() $C_v$
of
$C_v$
of
![]() ${\mathcal F}_P$
are indexed by vertices v, such that
${\mathcal F}_P$
are indexed by vertices v, such that
![]() $C_v$
is the positive span of the vectors
$C_v$
is the positive span of the vectors
![]() $h_i - h_j$
for
$h_i - h_j$
for
![]() $j \to i$
an edge of
$j \to i$
an edge of
![]() $T_v$
.
$T_v$
.
The first part of the following result is similar to [Reference PostnikovPo09, Lemma 13.2].
Lemma 8.2. Let P be a generic simple alcoved polytope, and v a vertex of P. Then the tree
![]() $T_v$
is alternating. Furthermore, if P is a polypositroid, then
$T_v$
is alternating. Furthermore, if P is a polypositroid, then
![]() $T_v$
is in addition noncrossing.
$T_v$
is in addition noncrossing.
Proof. If
![]() $j \to i$
and
$j \to i$
and
![]() $k \to j$
both belong to
$k \to j$
both belong to
![]() $T_v$
, then
$T_v$
, then
![]() $h_i - h_k \in C_v$
and is not one of the edges of
$h_i - h_k \in C_v$
and is not one of the edges of
![]() $C_v$
, contradicting the assumption that all roots are edges of
$C_v$
, contradicting the assumption that all roots are edges of
![]() ${\mathcal F}_P$
. We conclude that
${\mathcal F}_P$
. We conclude that
![]() $T_v$
is alternating.
$T_v$
is alternating.
Now suppose that P is a polypositroid. Since P is generic and simple, the polytope
![]() $P'$
obtained from a small perturbation of the facets of P will have the same combinatorial type as P. We can pick such a
$P'$
obtained from a small perturbation of the facets of P will have the same combinatorial type as P. We can pick such a
![]() $P'$
to be a polypositroid
$P'$
to be a polypositroid
![]() $Q(\mathbf {v})$
for a generic Coxeter necklace
$Q(\mathbf {v})$
for a generic Coxeter necklace
![]() $\mathbf {v}$
. It follows from Lemma 6.17 that the trees
$\mathbf {v}$
. It follows from Lemma 6.17 that the trees
![]() $T_v$
are noncrossing.
$T_v$
are noncrossing.
Suppose T is an alternating tree
![]() $[n]$
. A matching of
$[n]$
. A matching of
![]() $(I,J)$
in T is a collection of edges of T which form a matching of I with J, such that vertices in I are sources, and the vertices in J are sinks. Say that two directed alternating trees
$(I,J)$
in T is a collection of edges of T which form a matching of I with J, such that vertices in I are sources, and the vertices in J are sinks. Say that two directed alternating trees
![]() $T,T'$
on
$T,T'$
on
![]() $[n]$
are compatible if there do not exist disjoint subsets
$[n]$
are compatible if there do not exist disjoint subsets
![]() $I, J \subset [n]$
of the same cardinality, such that both T and
$I, J \subset [n]$
of the same cardinality, such that both T and
![]() $T'$
contain matchings of
$T'$
contain matchings of
![]() $(I,J)$
, and these matchings disagree.
$(I,J)$
, and these matchings disagree.
Lemma 8.3 (cf. [Reference PostnikovPo09, Lemma 12.6])
Let
![]() $T, T'$
be distinct directed alternating trees on
$T, T'$
be distinct directed alternating trees on
![]() $[n]$
. The intersection
$[n]$
. The intersection
![]() $C_T \cap C_{T'}$
is a common face of both
$C_T \cap C_{T'}$
is a common face of both
![]() $C_T$
and
$C_T$
and
![]() $C_{T'}$
if and only if T and
$C_{T'}$
if and only if T and
![]() $T'$
are compatible.
$T'$
are compatible.
Proof. Suppose T and
![]() $T'$
are not compatible. Let
$T'$
are not compatible. Let
![]() $I, J \subset [n]$
be disjoint, such that T (respectively,
$I, J \subset [n]$
be disjoint, such that T (respectively,
![]() $T'$
) contains a matching M (respectively,
$T'$
) contains a matching M (respectively,
![]() $M'$
) from I to J, such that
$M'$
) from I to J, such that
![]() $M \neq M'$
. We assume that I and J are chosen to be minimal, so that
$M \neq M'$
. We assume that I and J are chosen to be minimal, so that
![]() $M \cap M' = \emptyset $
. Let
$M \cap M' = \emptyset $
. Let
 $$ \begin{align*}x=\sum_{j \in J} h_j - \sum_{i \in I} h_i = \sum_{(i \to j) \in M} h_j - h_i = \sum_{(i \to j) \in M'} h_j - h_i. \end{align*} $$
$$ \begin{align*}x=\sum_{j \in J} h_j - \sum_{i \in I} h_i = \sum_{(i \to j) \in M} h_j - h_i = \sum_{(i \to j) \in M'} h_j - h_i. \end{align*} $$
Clearly,
![]() $x \in C_T \cap C_{T'}$
. The minimal face of
$x \in C_T \cap C_{T'}$
. The minimal face of
![]() $C_T$
containing x is
$C_T$
containing x is
![]() $C_M$
. The minimal face of
$C_M$
. The minimal face of
![]() $C_{T'}$
containing x is
$C_{T'}$
containing x is
![]() $C_{M'}$
. Since
$C_{M'}$
. Since
![]() $M \neq M'$
, we conclude that
$M \neq M'$
, we conclude that
![]() $C_T \cap C_{T'}$
is not a common face.
$C_T \cap C_{T'}$
is not a common face.
Conversely, suppose that T and
![]() $T'$
are compatible. Let
$T'$
are compatible. Let
![]() $F = T \cap T'$
be the intersection, a directed forest on
$F = T \cap T'$
be the intersection, a directed forest on
![]() $[n]$
. Define a partial order
$[n]$
. Define a partial order
![]() $\prec $
on the connected components (denoted A) of F, by letting
$\prec $
on the connected components (denoted A) of F, by letting
![]() $A \prec A'$
if there is a (necessarily unique) sequence
$A \prec A'$
if there is a (necessarily unique) sequence
![]() $A=A_0, A_1, \ldots ,A_{\ell } = A'$
of distinct components of F, such that T has a (unique) directed edge
$A=A_0, A_1, \ldots ,A_{\ell } = A'$
of distinct components of F, such that T has a (unique) directed edge
![]() $f_i$
joining
$f_i$
joining
![]() $A_i$
to
$A_i$
to
![]() $A_{i+1}$
for
$A_{i+1}$
for
![]() $i \in [0,\ell -1]$
. Similarly, define
$i \in [0,\ell -1]$
. Similarly, define
![]() $\prec '$
using
$\prec '$
using
![]() $T'$
. We claim that
$T'$
. We claim that
![]() $A \prec A'$
if and only if
$A \prec A'$
if and only if
![]() $A' \prec ' A$
. Assuming otherwise, the sequence of components from A to
$A' \prec ' A$
. Assuming otherwise, the sequence of components from A to
![]() $A'$
for T and from
$A'$
for T and from
![]() $A'$
to A for
$A'$
to A for
![]() $T'$
can be assumed to be distinct except for A and
$T'$
can be assumed to be distinct except for A and
![]() $A'$
. Using the directed edges
$A'$
. Using the directed edges
![]() $f_i \in T$
from A to
$f_i \in T$
from A to
![]() $A'$
and
$A'$
and
![]() $g_i \in T'$
from
$g_i \in T'$
from
![]() $A'$
to A, together with some of the edges in F, one obtains an alternating cycle of even length, such that (picking an orientation) the clockwise edges belong to T, and the counterclockwise edges belong to
$A'$
to A, together with some of the edges in F, one obtains an alternating cycle of even length, such that (picking an orientation) the clockwise edges belong to T, and the counterclockwise edges belong to
![]() $T'$
. This immediately contradicts the compatibility of T and
$T'$
. This immediately contradicts the compatibility of T and
![]() $T'$
.
$T'$
.
Now, let
![]() $f:[n] \to \mathbb {R}$
be a function with the following properties: it is constant with value
$f:[n] \to \mathbb {R}$
be a function with the following properties: it is constant with value
![]() $f(A)$
on the components A of F, and such that
$f(A)$
on the components A of F, and such that
![]() $f(A) < f(A')$
if and only if
$f(A) < f(A')$
if and only if
![]() $A \prec A'$
if and only if
$A \prec A'$
if and only if
![]() $A' \prec ' A$
. Assume that
$A' \prec ' A$
. Assume that
![]() $f(n) = 0$
. Then f extends to a linear function
$f(n) = 0$
. Then f extends to a linear function
![]() $\phi _f: (\mathbb {R}^n)^*/h_n \mapsto \mathbb {R}$
, by setting
$\phi _f: (\mathbb {R}^n)^*/h_n \mapsto \mathbb {R}$
, by setting
![]() $h_i \mapsto f(i)$
. It follows by construction that
$h_i \mapsto f(i)$
. It follows by construction that
![]() $\phi _f(C_T) \geq 0$
,
$\phi _f(C_T) \geq 0$
,
![]() $\phi _f(C_{T'}) \leq 0$
, and
$\phi _f(C_{T'}) \leq 0$
, and
![]() $\phi _f(C_F) = 0$
. It follows that
$\phi _f(C_F) = 0$
. It follows that
![]() $C_T \cap C_{T'} = C_F$
is a common face of both cones.
$C_T \cap C_{T'} = C_F$
is a common face of both cones.
A matching field on
![]() $[n]$
is a collection
$[n]$
is a collection
![]() ${\mathcal {E}} = \{M_{I,J}\}$
of matchings, one for each pair
${\mathcal {E}} = \{M_{I,J}\}$
of matchings, one for each pair
![]() $(I,J)$
of disjoint subsets of
$(I,J)$
of disjoint subsets of
![]() $[n]$
of equal size, such that for each
$[n]$
of equal size, such that for each
![]() $I' \subset I$
and
$I' \subset I$
and
![]() $J' \subset J$
, where
$J' \subset J$
, where
![]() $I'$
is matched to
$I'$
is matched to
![]() $J'$
in
$J'$
in
![]() $M_{I,J}$
, we have
$M_{I,J}$
, we have
![]() $M_{I',J'}$
is the restriction of
$M_{I',J'}$
is the restriction of
![]() $M_{I,J}$
to
$M_{I,J}$
to
![]() $(I',J')$
. If
$(I',J')$
. If
![]() $M_{I',J'}$
is a restriction of
$M_{I',J'}$
is a restriction of
![]() $M_{I,J}$
, we shall say that
$M_{I,J}$
, we shall say that
![]() $M_{I,J}$
contains
$M_{I,J}$
contains
![]() $M_{I',J'}$
.
$M_{I',J'}$
.
We shall call a matching field noncrossing, if every matching
![]() $M_{I,J}$
is noncrossing when drawn on the circle.
$M_{I,J}$
is noncrossing when drawn on the circle.
Theorem 8.4. For each generic simple alcoved polytope P, there is a unique matching field
![]() ${\mathcal {E}}(P)$
, such that
${\mathcal {E}}(P)$
, such that
![]() ${\mathcal {E}}(P)$
and the set of vertex trees
${\mathcal {E}}(P)$
and the set of vertex trees
![]() ${\mathcal {T}}(P)$
are related by the condition:
${\mathcal {T}}(P)$
are related by the condition:
![]() $T \in {\mathcal {T}}(P)$
if and only if all matchings in T belong to the
$T \in {\mathcal {T}}(P)$
if and only if all matchings in T belong to the
![]() ${\mathcal {E}}(P)$
.
${\mathcal {E}}(P)$
.
Furthermore, if P is a polypositroid, then
![]() ${\mathcal {E}}(P)$
consists of noncrossing trees.
${\mathcal {E}}(P)$
consists of noncrossing trees.
Proof. Let P be a generic simple alcoved polytope, and
![]() ${\mathcal {T}}(P)$
be its set of vertex trees. We claim that for each pair
${\mathcal {T}}(P)$
be its set of vertex trees. We claim that for each pair
![]() $(I,J)$
of disjoint subsets of
$(I,J)$
of disjoint subsets of
![]() $[n]$
of equal cardinality, some tree
$[n]$
of equal cardinality, some tree
![]() $T \in {\mathcal {T}}(P)$
contains a matching of
$T \in {\mathcal {T}}(P)$
contains a matching of
![]() $(I,J)$
. To see this, consider the point
$(I,J)$
. To see this, consider the point
![]() $x_{I,J}=\sum _{j \in J} h_j - \sum _{i \in I} h_i$
. Since
$x_{I,J}=\sum _{j \in J} h_j - \sum _{i \in I} h_i$
. Since
![]() $\{C_T \mid T \in {\mathcal {T}}(P)\}$
are the maximal cones of a complete fan, it belongs to
$\{C_T \mid T \in {\mathcal {T}}(P)\}$
are the maximal cones of a complete fan, it belongs to
![]() $C_T$
for some
$C_T$
for some
![]() $T \in {\mathcal {T}}(P)$
. But T is alternating by Lemma 8.2, and it follows that T contains a unique matching of
$T \in {\mathcal {T}}(P)$
. But T is alternating by Lemma 8.2, and it follows that T contains a unique matching of
![]() $(I,J)$
. It follows from Lemma 8.3 that
$(I,J)$
. It follows from Lemma 8.3 that
![]() ${\mathcal {T}}(P)$
determines a unique matching ensemble
${\mathcal {T}}(P)$
determines a unique matching ensemble
![]() ${\mathcal {E}}(P)$
. Furthermore,
${\mathcal {E}}(P)$
. Furthermore,
![]() ${\mathcal {T}}(P)$
is exactly the set of trees T, such that all matchings in T belong to
${\mathcal {T}}(P)$
is exactly the set of trees T, such that all matchings in T belong to
![]() ${\mathcal {E}}(P)$
: if
${\mathcal {E}}(P)$
: if
![]() $T'$
is another tree satisfying this condition, then, by Lemma 8.3,
$T'$
is another tree satisfying this condition, then, by Lemma 8.3,
![]() $C_{T'}$
can be added to the complete fan
$C_{T'}$
can be added to the complete fan
![]() $\{C_T \mid T \in {\mathcal {T}}(P)\}$
, which is a contradiction.
$\{C_T \mid T \in {\mathcal {T}}(P)\}$
, which is a contradiction.
The last sentence follows from Lemma 8.2.
Definition 8.5 (cf. [Reference Oh and YooOY, Reference Sturmfels and ZelevinskySZ])
Let
![]() ${\mathcal {E}}$
be a matching field. Then we say that
${\mathcal {E}}$
be a matching field. Then we say that
![]() ${\mathcal {E}}$
satisfies the linkage axiom if
${\mathcal {E}}$
satisfies the linkage axiom if
-
1. for any disjoint
 $(I,J)$
of equal size, and
$(I,J)$
of equal size, and
 $j' \in [n] \setminus (I \cup J)$
, there is an edge
$j' \in [n] \setminus (I \cup J)$
, there is an edge
 $(i,j) \in M_{I,J}$
, such that the matching
$(i,j) \in M_{I,J}$
, such that the matching
 $M^{\prime }_{I,J'} := M_{I,J} \setminus \{(i,j)\} \cup \{(i,j')\}$
belongs to
$M^{\prime }_{I,J'} := M_{I,J} \setminus \{(i,j)\} \cup \{(i,j')\}$
belongs to
 ${\mathcal {E}}$
, where
${\mathcal {E}}$
, where
 $J' = J \setminus \{j\} \cup \{j'\}$
;
$J' = J \setminus \{j\} \cup \{j'\}$
; -
2. for any disjoint
 $(I,J)$
of equal size, and
$(I,J)$
of equal size, and
 $i'\, \in [n] \setminus (I \cup J)$
, there is an edge
$i'\, \in [n] \setminus (I \cup J)$
, there is an edge
 $(i,j) \in M_{I,J}$
, such that the matching
$(i,j) \in M_{I,J}$
, such that the matching
 $M^{\prime }_{I',J} := M_{I,J} \setminus \{(i,j)\} \cup \{(i',j)\}$
belongs to
$M^{\prime }_{I',J} := M_{I,J} \setminus \{(i,j)\} \cup \{(i',j)\}$
belongs to
 ${\mathcal {E}}$
, where
${\mathcal {E}}$
, where
 $I' = I \setminus \{i\} \cup \{i'\}$
;
$I' = I \setminus \{i\} \cup \{i'\}$
;
If
![]() ${\mathcal {E}}$
satisfies the linkage axiom, we say that
${\mathcal {E}}$
satisfies the linkage axiom, we say that
![]() ${\mathcal {E}}$
is a matching ensemble.
${\mathcal {E}}$
is a matching ensemble.
Proposition 8.6. Let P be a generic simple alcoved polytope, and let
![]() ${\mathcal {E}}(P)$
be the appearing in Theorem 8.4. Then
${\mathcal {E}}(P)$
be the appearing in Theorem 8.4. Then
![]() ${\mathcal {E}}(P)$
satisfies the linkage axiom, and is a matching ensemble.
${\mathcal {E}}(P)$
satisfies the linkage axiom, and is a matching ensemble.
Proof. Let
![]() $k = |I| = |J|$
. Consider the vector
$k = |I| = |J|$
. Consider the vector
 $$ \begin{align*}x = \left(1+ \frac{1}{k}\right)\sum_{i \in I} h_i + \sum_{j \in J \cup\{j'\}} h_j. \end{align*} $$
$$ \begin{align*}x = \left(1+ \frac{1}{k}\right)\sum_{i \in I} h_i + \sum_{j \in J \cup\{j'\}} h_j. \end{align*} $$
Then x lies in the cone
![]() $C_T$
for some
$C_T$
for some
![]() $T \in {\mathcal {T}}(P)$
. Let
$T \in {\mathcal {T}}(P)$
. Let
![]() $\tilde T = T|_{I \cup J \cup \{j'\}}$
denote the induced subgraph on
$\tilde T = T|_{I \cup J \cup \{j'\}}$
denote the induced subgraph on
![]() $I \cup J \cup \{j'\}$
. It is not difficult to see that
$I \cup J \cup \{j'\}$
. It is not difficult to see that
![]() $\tilde T$
must be connected, and thus itself a tree. Let
$\tilde T$
must be connected, and thus itself a tree. Let
![]() $A_1,A_2,\ldots ,A_r \subset I \cup J$
be the (vertex sets of the) connected components of the forest
$A_1,A_2,\ldots ,A_r \subset I \cup J$
be the (vertex sets of the) connected components of the forest
![]() $\tilde T \setminus \{j'\}$
obtained by removing
$\tilde T \setminus \{j'\}$
obtained by removing
![]() $j'$
. Looking at the coefficients of
$j'$
. Looking at the coefficients of
![]() $h_t$
,
$h_t$
,
![]() $t \in A_s$
in x, we deduce that
$t \in A_s$
in x, we deduce that
![]() $|A_s \cap I| = |A_s \cap J|$
for each
$|A_s \cap I| = |A_s \cap J|$
for each
![]() $s = 1,2,\ldots ,r$
. It follows that the matching
$s = 1,2,\ldots ,r$
. It follows that the matching
![]() $M_{I,J} \in {\mathcal {E}}(P)$
restricts to a matching on
$M_{I,J} \in {\mathcal {E}}(P)$
restricts to a matching on
![]() $(A_s \cap I, A_s \cap J)$
for each
$(A_s \cap I, A_s \cap J)$
for each
![]() $s = 1,2,\ldots ,r$
.
$s = 1,2,\ldots ,r$
.
Now let
![]() $i \in (A_1 \cap I)$
be the vertex in
$i \in (A_1 \cap I)$
be the vertex in
![]() $A_1$
connected to
$A_1$
connected to
![]() $j'$
and let
$j'$
and let
![]() $(i,j) \in M_{I,J}$
be the edge of
$(i,j) \in M_{I,J}$
be the edge of
![]() $M_{I,J}$
incident to i. Then T also contains the matching
$M_{I,J}$
incident to i. Then T also contains the matching
![]() $M_{I,J} \setminus \{(i,j)\} \cup \{(i,j')\}$
, and, by Theorem 8.4, so does
$M_{I,J} \setminus \{(i,j)\} \cup \{(i,j')\}$
, and, by Theorem 8.4, so does
![]() ${\mathcal {E}}(P)$
. This establishes condition (1) of the linkage axiom for
${\mathcal {E}}(P)$
. This establishes condition (1) of the linkage axiom for
![]() ${\mathcal {E}}(P)$
. Condition (2) is similar.
${\mathcal {E}}(P)$
. Condition (2) is similar.
Conjecture 8.7. Every noncrossing matching ensemble appears as
![]() ${\mathcal {E}}(P)$
for some generic simple polypositroid P.
${\mathcal {E}}(P)$
for some generic simple polypositroid P.
Remark 8.8. In some way, matching ensembles are analogous to matroids, and matching ensembles of the form
![]() ${\mathcal {E}}(P)$
are analogous to realizable matroids. So Conjecture 8.7 is similar in spirit to the result of [Reference Ardila, Rincón and WilliamsARW17] that positive oriented matroids are positroids, that is, they are realizable.
${\mathcal {E}}(P)$
are analogous to realizable matroids. So Conjecture 8.7 is similar in spirit to the result of [Reference Ardila, Rincón and WilliamsARW17] that positive oriented matroids are positroids, that is, they are realizable.
The following examples support Conjecture 8.7.
Example 8.9. Let
![]() $n =3$
. In this case, every alcoved polytope is automatically a polypositroid. Indeed, there is a single matching field on
$n =3$
. In this case, every alcoved polytope is automatically a polypositroid. Indeed, there is a single matching field on
![]() $\{1,2,3\}$
, it satisfies the linkage axiom, and it is noncrossing. Thus, there is only one possible normal fan for a generic simple polypositroid.
$\{1,2,3\}$
, it satisfies the linkage axiom, and it is noncrossing. Thus, there is only one possible normal fan for a generic simple polypositroid.
Example 8.10. Let
![]() $n = 4$
. Let P be a generic simple polypositroid. We use Theorem 8.4 to understand the possible choices for
$n = 4$
. Let P be a generic simple polypositroid. We use Theorem 8.4 to understand the possible choices for
![]() ${\mathcal {T}}(P)$
. By the noncrossing condition, a matching field
${\mathcal {T}}(P)$
. By the noncrossing condition, a matching field
![]() ${\mathcal {E}}(P)$
is uniquely determined except for matchings on
${\mathcal {E}}(P)$
is uniquely determined except for matchings on
![]() $(I,J) = (\{1,3\},\{2,4\})$
and
$(I,J) = (\{1,3\},\{2,4\})$
and
![]() $(I,J) = (\{2,4\},\{1,3\})$
, each of which there are two choices of matchings, giving four possibilities for
$(I,J) = (\{2,4\},\{1,3\})$
, each of which there are two choices of matchings, giving four possibilities for
![]() ${\mathcal {E}}(P)$
, all of which satisfy the linkage axiom. By an explicit calculation, for example, by computing whether putative vertices
${\mathcal {E}}(P)$
, all of which satisfy the linkage axiom. By an explicit calculation, for example, by computing whether putative vertices
![]() $v_T$
lie inside P, we find that the matching
$v_T$
lie inside P, we find that the matching
![]() $M_{\{1,3\},\{2,4\}}$
(respectively,
$M_{\{1,3\},\{2,4\}}$
(respectively,
![]() $M_{\{2,4\},\{1,3\}}$
) depends on the sign of
$M_{\{2,4\},\{1,3\}}$
) depends on the sign of
![]() $a_{41}+a_{23}- a_{43}-a_{21}$
(respectively,
$a_{41}+a_{23}- a_{43}-a_{21}$
(respectively,
![]() $a_{12}+a_{34} - a_{14}-a_{32}$
) (if
$a_{12}+a_{34} - a_{14}-a_{32}$
) (if
![]() $a_{41}+a_{23}- a_{43}-a_{21} = 0$
, then P is not simple). Suppose that P arises from the balanced graph G via Theorem 6.12. Then we have
$a_{41}+a_{23}- a_{43}-a_{21} = 0$
, then P is not simple). Suppose that P arises from the balanced graph G via Theorem 6.12. Then we have
(using (6.2), the right hand side (RHS) can be written in a number of equivalent ways). It is easy to construct generic balanced G, such that the RHS has any of the four possible ordered pairs of signs. For example, a balanced directed cycle
![]() $(1 \to 4 \to 3 \to 1)$
(respectively,
$(1 \to 4 \to 3 \to 1)$
(respectively,
![]() $(4 \to 3 \to 2 \to 4)$
) makes the first (respectively, second) quantity in (8.2) positive and the second (respectively, first) 0. It follows that there are exactly four normal fans of generic simple polypositroids for
$(4 \to 3 \to 2 \to 4)$
) makes the first (respectively, second) quantity in (8.2) positive and the second (respectively, first) 0. It follows that there are exactly four normal fans of generic simple polypositroids for
![]() $n = 4$
.
$n = 4$
.
We consider the cyclohedron defined in (3.5).
Proposition 8.11. Let P be a cyclohedron. Then the set
![]() ${\mathcal {T}}(P)$
of vertex trees of P is the set of noncrossing, alternating trees on
${\mathcal {T}}(P)$
of vertex trees of P is the set of noncrossing, alternating trees on
![]() $[n]$
with the following additional property: there is a cyclic rotation
$[n]$
with the following additional property: there is a cyclic rotation
![]() $i \prec i+1 \prec \cdots \prec n \prec 1 \prec \cdots \prec i-1$
of the usual order on
$i \prec i+1 \prec \cdots \prec n \prec 1 \prec \cdots \prec i-1$
of the usual order on
![]() $[n]$
, such that every edge
$[n]$
, such that every edge
![]() $(i,j)$
of
$(i,j)$
of
![]() $T_v$
satisfies
$T_v$
satisfies
![]() $i \prec j$
.
$i \prec j$
.
Proof. Let
![]() $r,s,r',s'$
be four indices in cyclic order. Then it follows from (3.6) that
$r,s,r',s'$
be four indices in cyclic order. Then it follows from (3.6) that
![]() $f_{[r,s]}+f_{[r',s']}> f_{[r,s']}+f_{[r',s]} - k $
, so that in any vertex tree
$f_{[r,s]}+f_{[r',s']}> f_{[r,s']}+f_{[r',s]} - k $
, so that in any vertex tree
![]() $T_v$
, the directed edges
$T_v$
, the directed edges
![]() $(r-1) \to s$
and
$(r-1) \to s$
and
![]() $(r'-1) \to s'$
cannot both be present. The set of trees satisfying this condition is exactly the set of trees stated in the proposition. To complete the proof, it suffices to note from (8.1) that the cyclohedron has
$(r'-1) \to s'$
cannot both be present. The set of trees satisfying this condition is exactly the set of trees stated in the proposition. To complete the proof, it suffices to note from (8.1) that the cyclohedron has
![]() $\binom {2n-2}{n-1}$
vertices, and that the number of noncrossing, decreasing (every edge
$\binom {2n-2}{n-1}$
vertices, and that the number of noncrossing, decreasing (every edge
![]() $(i \to j)$
satisfies
$(i \to j)$
satisfies
![]() $j < i$
), alternating trees on
$j < i$
), alternating trees on
![]() $[n]$
is equal to the Catalan number
$[n]$
is equal to the Catalan number
![]() $\frac {1}{n}\binom {2n-2}{n-1}$
(see [Reference PostnikovPo09] or Remark 8.21 below).
$\frac {1}{n}\binom {2n-2}{n-1}$
(see [Reference PostnikovPo09] or Remark 8.21 below).
For example, let
![]() $n = 4$
. Then the cyclohedron has
$n = 4$
. Then the cyclohedron has
![]() $20$
vertices, and each vertex tree is a rotation of one of the trees in Figure 1.
$20$
vertices, and each vertex tree is a rotation of one of the trees in Figure 1.
Figure 1 Noncrossing, decreasing, alternating trees on
![]() $\{1,2,3,4\}$
.
$\{1,2,3,4\}$
.
Remark 8.12. The decomposition in Proposition 8.11 of
![]() ${\mathcal {T}}(P)$
into the n cyclic rotations of the set of noncrossing, alternating, decreasing trees has the following geometric interpretation: the cones
${\mathcal {T}}(P)$
into the n cyclic rotations of the set of noncrossing, alternating, decreasing trees has the following geometric interpretation: the cones
![]() $C, c(C), c^2(C),\ldots ,c^{n-1}(C)$
cover all of
$C, c(C), c^2(C),\ldots ,c^{n-1}(C)$
cover all of
![]() $H_0$
and intersect in lower-dimensional faces.
$H_0$
and intersect in lower-dimensional faces.
8.3. Proof of Theorem 4.9
Proposition 8.13. Let P be a generic simple alcoved polytope given by the inequalities (3.2). Then P is a polypositroid if and only if, for any four indices
![]() $i,j,k,l$
in cyclic order, we have
$i,j,k,l$
in cyclic order, we have
![]() $a_{ik} + a_{jl}> a_{il} + a_{jk}$
.
$a_{ik} + a_{jl}> a_{il} + a_{jk}$
.
Proof. Suppose P is a generic simple polypositroid. By the uniqueness part of Theorem 8.4 (or directly from the proof), there is a vertex tree
![]() $T_v$
of P, which contains a noncrossing matching of
$T_v$
of P, which contains a noncrossing matching of
![]() $(\{k,l\},\{i,j\})$
. Since
$(\{k,l\},\{i,j\})$
. Since
![]() $i,j,k,l$
are in cyclic order, the matching must match i with l and match j with k. We thus have
$i,j,k,l$
are in cyclic order, the matching must match i with l and match j with k. We thus have
 $$ \begin{align*} a_{il} + a_{jk} &= (h_{i}-h_{l})(v) +(h_j - h_k)(v) \\ &= (h_i - h_k)(v) + (h_j - h_l)(v) \\ &\leq a_{ik} + a_{jl}. \end{align*} $$
$$ \begin{align*} a_{il} + a_{jk} &= (h_{i}-h_{l})(v) +(h_j - h_k)(v) \\ &= (h_i - h_k)(v) + (h_j - h_l)(v) \\ &\leq a_{ik} + a_{jl}. \end{align*} $$
Equality cannot occur, for otherwise,
![]() $T_v$
will contain a cycle. Conversely, if P is a generic simple alcoved polytope and
$T_v$
will contain a cycle. Conversely, if P is a generic simple alcoved polytope and
![]() $a_{ik} + a_{jl}> a_{il} + a_{jk}$
holds for any four indices
$a_{ik} + a_{jl}> a_{il} + a_{jk}$
holds for any four indices
![]() $i,j,k,l$
in cyclic order, then we deduce that
$i,j,k,l$
in cyclic order, then we deduce that
![]() ${\mathcal {E}}(P)$
is noncrossing, so
${\mathcal {E}}(P)$
is noncrossing, so
![]() ${\mathcal {T}}(P)$
consists of noncrossing trees, and, by Lemma 6.15, we conclude that P is a polypositroid.
${\mathcal {T}}(P)$
consists of noncrossing trees, and, by Lemma 6.15, we conclude that P is a polypositroid.
Now, the inequalities
![]() $a_{ik} + a_{jl}> a_{il} + a_{jk}$
define an open subcone C of
$a_{ik} + a_{jl}> a_{il} + a_{jk}$
define an open subcone C of
![]() ${\mathcal {C}}_{\mathrm { alc}}$
, each point of which represents a generic alcoved polytope. It follows from Proposition 8.11 that the cyclohedron is a generic simple polypositroid and thus C is nonempty. An open dense subset of
${\mathcal {C}}_{\mathrm { alc}}$
, each point of which represents a generic alcoved polytope. It follows from Proposition 8.11 that the cyclohedron is a generic simple polypositroid and thus C is nonempty. An open dense subset of
![]() $C' \subseteq C$
corresponds to generic alcoved polytopes that are simple. Applying Proposition 8.13, we see that these polytopes are generic simple polypositroids. The closure of
$C' \subseteq C$
corresponds to generic alcoved polytopes that are simple. Applying Proposition 8.13, we see that these polytopes are generic simple polypositroids. The closure of
![]() $C'$
is the closed cone cut out by (4.3). The corresponding limits of generic simple polypositroids are nonempty (possibly not generic, possibly not simple) polypositroids, finishing the proof of the Theorem 4.9.
$C'$
is the closed cone cut out by (4.3). The corresponding limits of generic simple polypositroids are nonempty (possibly not generic, possibly not simple) polypositroids, finishing the proof of the Theorem 4.9.
8.4. Duality for alternating trees
A noncrossing tree T on
![]() $[n]$
is called circular-alternating if for each vertex v, the edges incident to v alternate between incoming and outgoing as they are read in order when
$[n]$
is called circular-alternating if for each vertex v, the edges incident to v alternate between incoming and outgoing as they are read in order when
![]() $T_v$
is drawn on a circle. Thus, for example, if v is incident to
$T_v$
is drawn on a circle. Thus, for example, if v is incident to
![]() $u_1,u_2,u_3,u_4$
with
$u_1,u_2,u_3,u_4$
with
![]() $u_1<v<u_2<u_3<u_4$
, then the edges
$u_1<v<u_2<u_3<u_4$
, then the edges
![]() $(v,u_1)$
,
$(v,u_1)$
,
![]() $(v,u_4)$
,
$(v,u_4)$
,
![]() $(v,u_3)$
,
$(v,u_3)$
,
![]() $(v,u_2)$
alternate in direction.
$(v,u_2)$
alternate in direction.
Let
![]() ${\mathcal {T}}_{\mathrm {alt}}$
denote the set of alternating, noncrossing trees, and let
${\mathcal {T}}_{\mathrm {alt}}$
denote the set of alternating, noncrossing trees, and let
![]() ${\mathcal {T}}_{\mathrm {cir}}$
denote the set of noncrossing, circular-alternating trees. For
${\mathcal {T}}_{\mathrm {cir}}$
denote the set of noncrossing, circular-alternating trees. For
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
, let
$T \in {\mathcal {T}}_{\mathrm {alt}}$
, let
![]() $T'$
be obtained from T as follows: place the numbers
$T'$
be obtained from T as follows: place the numbers
![]() $1',1,2',2,\ldots ,n',n$
in clockwise order around a circle, and draw T using the numbers
$1',1,2',2,\ldots ,n',n$
in clockwise order around a circle, and draw T using the numbers
![]() $1,2,\ldots ,n$
. Then
$1,2,\ldots ,n$
. Then
![]() $T'$
is the unique tree on the numbers
$T'$
is the unique tree on the numbers
![]() $1',2',\ldots ,n'$
, such that each directed edge
$1',2',\ldots ,n'$
, such that each directed edge
![]() $c' \to d'$
of
$c' \to d'$
of
![]() $T'$
intersects a unique directed edge
$T'$
intersects a unique directed edge
![]() $a \to b$
of T, and furthermore,
$a \to b$
of T, and furthermore,
![]() $a, d', b, c'$
are in clockwise order.
$a, d', b, c'$
are in clockwise order.
Proposition 8.14. The map
![]() $T \mapsto T'$
gives a bijection
$T \mapsto T'$
gives a bijection
![]() $\varphi : {\mathcal {T}}_{\mathrm {alt}} \to {\mathcal {T}}_{\mathrm { cir}}$
.
$\varphi : {\mathcal {T}}_{\mathrm {alt}} \to {\mathcal {T}}_{\mathrm { cir}}$
.
Proof. The tree T cuts the disk up into n pieces, each containing exactly one of
![]() $1',2',\ldots ,n'$
. Let D be one of these components. Then D is bounded by an arc of the circle and a number of edges of T. When read in order around the boundary of D, these edges of T alternate in direction. It follows that
$1',2',\ldots ,n'$
. Let D be one of these components. Then D is bounded by an arc of the circle and a number of edges of T. When read in order around the boundary of D, these edges of T alternate in direction. It follows that
![]() $T' \in {\mathcal {T}}_{\mathrm {cir}}$
.
$T' \in {\mathcal {T}}_{\mathrm {cir}}$
.
In the other direction, let
![]() $D'$
be one of the components that
$D'$
be one of the components that
![]() $T' \in {\mathcal {T}}_{\mathrm {cir}}$
divides the disk into. Then the edges of
$T' \in {\mathcal {T}}_{\mathrm {cir}}$
divides the disk into. Then the edges of
![]() $T'$
along the boundary of
$T'$
along the boundary of
![]() $D'$
are all in the same direction. It follows that there is unique
$D'$
are all in the same direction. It follows that there is unique
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
, such that
$T \in {\mathcal {T}}_{\mathrm {alt}}$
, such that
![]() $\varphi (T) = T'$
.
$\varphi (T) = T'$
.
For a tree T, let
![]() $C^{\prime }_T$
denote the cone in
$C^{\prime }_T$
denote the cone in
![]() $\mathbb {R}^n$
spanned by
$\mathbb {R}^n$
spanned by
![]() $e_i - e_j$
for each directed edge
$e_i - e_j$
for each directed edge
![]() $j \to i$
in T.
$j \to i$
in T.
Proposition 8.15. For
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
, the cones
$T \in {\mathcal {T}}_{\mathrm {alt}}$
, the cones
![]() $C_T$
and
$C_T$
and
![]() $C^{\prime }_{\varphi (T)}$
are dual cones.
$C^{\prime }_{\varphi (T)}$
are dual cones.
Proof. We have
 $$ \begin{align*}(h_b - h_a)(e_{d}-e_{c}) = \begin{cases} 0 & \mbox{if } \overline{ab} \mbox{ and } \overline{d'a'} \mbox{ are noncrossing,} \\ 1 & \mbox{if } a,d',b,c' \mbox{ are in clockwise order,} \\ -1 & \mbox{if } a,d',b,c' \mbox{ are in anticlockwise order.} \end{cases} \end{align*} $$
$$ \begin{align*}(h_b - h_a)(e_{d}-e_{c}) = \begin{cases} 0 & \mbox{if } \overline{ab} \mbox{ and } \overline{d'a'} \mbox{ are noncrossing,} \\ 1 & \mbox{if } a,d',b,c' \mbox{ are in clockwise order,} \\ -1 & \mbox{if } a,d',b,c' \mbox{ are in anticlockwise order.} \end{cases} \end{align*} $$
The result then follows from the definition of
![]() $\varphi $
.
$\varphi $
.
Example 8.16. A noncrossing alternating tree
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
and the corresponding noncrossing, circular-alternating tree
$T \in {\mathcal {T}}_{\mathrm {alt}}$
and the corresponding noncrossing, circular-alternating tree
![]() ${\mathcal {T}}'=\varphi (T)$
is given in Figure 2. One can check that the cones
${\mathcal {T}}'=\varphi (T)$
is given in Figure 2. One can check that the cones
![]() $C_T = \mathrm {span}_{\geq 0}(h_3-h_4, h_2-h_4,h_2-h_6,h_2-h_1,h_5-h_6)$
and
$C_T = \mathrm {span}_{\geq 0}(h_3-h_4, h_2-h_4,h_2-h_6,h_2-h_1,h_5-h_6)$
and
![]() $C^{\prime }_{T'}=\mathrm { span}_{\geq 0}(e_3-e_4, e_5-e_3,e_1-e_5,e_2-e_1,e_5-e_6)$
are dual, in agreement with Proposition 8.15.
$C^{\prime }_{T'}=\mathrm { span}_{\geq 0}(e_3-e_4, e_5-e_3,e_1-e_5,e_2-e_1,e_5-e_6)$
are dual, in agreement with Proposition 8.15.

Figure 2 The bijection of Proposition 8.14: when T is the graph consisting of the solid arrows,
![]() $T' = \varphi (T)$
is the graph consisting of the dashed arrows.
$T' = \varphi (T)$
is the graph consisting of the dashed arrows.
Let T be a directed tree on
![]() $[n]$
. An edge is directed away from n if it is directed away from n as part of some path connected to n. Define two statistics on T by
$[n]$
. An edge is directed away from n if it is directed away from n as part of some path connected to n. Define two statistics on T by
 $$ \begin{align*} \mathrm{up}(T) &= \#\{ \text{edges directed away from } n\} \\ \mathrm{des}(T) &= \#\{ \text{edges } i \to j \text{ with } i> j\}. \end{align*} $$
$$ \begin{align*} \mathrm{up}(T) &= \#\{ \text{edges directed away from } n\} \\ \mathrm{des}(T) &= \#\{ \text{edges } i \to j \text{ with } i> j\}. \end{align*} $$
The edges counted by
![]() $\mathrm {des}(T)$
are called descent edges.
$\mathrm {des}(T)$
are called descent edges.
Proposition 8.17. Let
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
and
$T \in {\mathcal {T}}_{\mathrm {alt}}$
and
![]() $T' = \varphi (T) \in {\mathcal {T}}_{\mathrm {cir}}$
. Suppose that
$T' = \varphi (T) \in {\mathcal {T}}_{\mathrm {cir}}$
. Suppose that
![]() $e \in T$
is the unique edge intersecting
$e \in T$
is the unique edge intersecting
![]() $e' \in T' $
. Then e is directed away from n in T if and only if
$e' \in T' $
. Then e is directed away from n in T if and only if
![]() $e'$
is a descent edge in
$e'$
is a descent edge in
![]() $T'$
. In particular, we have
$T'$
. In particular, we have
![]() $\mathrm {up}(T) = \mathrm {des}(T')$
.
$\mathrm {up}(T) = \mathrm {des}(T')$
.
Let P be a generic simple polypositroid. Let
![]() ${\mathcal {T}}(P) = \{T_v\}$
be the collection of its vertex trees: by Lemma 8.2,
${\mathcal {T}}(P) = \{T_v\}$
be the collection of its vertex trees: by Lemma 8.2,
![]() ${\mathcal {T}}(P) \subset {\mathcal {T}}_{\mathrm {alt}}$
.
${\mathcal {T}}(P) \subset {\mathcal {T}}_{\mathrm {alt}}$
.
We now describe the 1-skeleton of P in terms of the trees
![]() $T_v$
. Suppose
$T_v$
. Suppose
![]() $E = (v,v')$
is an edge of P. The forest
$E = (v,v')$
is an edge of P. The forest
![]() $T_E$
has two components and one has
$T_E$
has two components and one has
![]() $T_v = T_E \cup \{e\}$
and
$T_v = T_E \cup \{e\}$
and
![]() $T_{v'} = T_E \cup \{e'\}$
for distinct directed edges
$T_{v'} = T_E \cup \{e'\}$
for distinct directed edges
![]() $e,e'$
. The graph
$e,e'$
. The graph
![]() $T_E \cup \{e,e'\}$
has a unique (nondirected) cycle containing both e and
$T_E \cup \{e,e'\}$
has a unique (nondirected) cycle containing both e and
![]() $e'$
.
$e'$
.
Lemma 8.18. The edges e and
![]() $e'$
have the same direction along this cycle.
$e'$
have the same direction along this cycle.
Proof. The edges e and
![]() $e'$
correspond to facets intersecting the edge E, and the direction corresponds to a choice of one infinite direction along the affine span of E, which we assume to be parallel to
$e'$
correspond to facets intersecting the edge E, and the direction corresponds to a choice of one infinite direction along the affine span of E, which we assume to be parallel to
![]() $e_i - e_j$
. The direction is determined by which of the two components
$e_i - e_j$
. The direction is determined by which of the two components
![]() $T_1$
and
$T_1$
and
![]() $T_2$
of
$T_2$
of
![]() $T_E$
the source (and hence sink) of e (respectively,
$T_E$
the source (and hence sink) of e (respectively,
![]() $e'$
) lies in. Indeed, if e goes from
$e'$
) lies in. Indeed, if e goes from
![]() $T_1$
to
$T_1$
to
![]() $T_2$
, and
$T_2$
, and
![]() $i \in T_1$
while
$i \in T_1$
while
![]() $j \in T_2$
, then the facet corresponding to e bounds the coordinate
$j \in T_2$
, then the facet corresponding to e bounds the coordinate
![]() $x_j$
above. It follows that the ray in the direction of
$x_j$
above. It follows that the ray in the direction of
![]() $v'$
emitting from v goes in the direction
$v'$
emitting from v goes in the direction
![]() $\mathbb {R}_{\geq 0}(e_i - e_j)$
.
$\mathbb {R}_{\geq 0}(e_i - e_j)$
.
But the two infinite directions corresponding to e and
![]() $e'$
are opposite, so e must go from
$e'$
are opposite, so e must go from
![]() $T_1$
to
$T_1$
to
![]() $T_2$
(without loss of generality), and
$T_2$
(without loss of generality), and
![]() $e'$
must go from
$e'$
must go from
![]() $T_2$
to
$T_2$
to
![]() $T_1$
. But this implies that e and
$T_1$
. But this implies that e and
![]() $e'$
have the same direction along the cycle containing them both.
$e'$
have the same direction along the cycle containing them both.
For a vertex v of a generalized permutohedron P, define the tree
![]() $T^{\prime }_v$
as follows (cf. [Reference Postnikov, Reiner and WilliamsPRW]):
$T^{\prime }_v$
as follows (cf. [Reference Postnikov, Reiner and WilliamsPRW]):
![]() $T^{\prime }_v$
has a directed edge
$T^{\prime }_v$
has a directed edge
![]() $j \to i$
if there is an edge incident with v which goes in the direction
$j \to i$
if there is an edge incident with v which goes in the direction
![]() $\mathbb {R}_{\geq 0}(e_i - e_j)$
. When P is a polypositroid, we thus have two directed trees
$\mathbb {R}_{\geq 0}(e_i - e_j)$
. When P is a polypositroid, we thus have two directed trees
![]() $T_v$
and
$T_v$
and
![]() $T^{\prime }_v$
on
$T^{\prime }_v$
on
![]() $[n]$
for each vertex
$[n]$
for each vertex
![]() $v \in P$
.
$v \in P$
.
Theorem 8.19. Let P be a generic simple polypositroid. Then for each vertex v of P, we have
![]() $T^{\prime }_v = \varphi (T_v)$
.
$T^{\prime }_v = \varphi (T_v)$
.
Proof. Suppose
![]() $e = (a \to b)$
is a directed edge of
$e = (a \to b)$
is a directed edge of
![]() $T_v$
, such that
$T_v$
, such that
![]() $T_v \backslash \{e\}$
has two components
$T_v \backslash \{e\}$
has two components
![]() $T_1 \ni a$
and
$T_1 \ni a$
and
![]() $T_2 \ni b$
. Let c be the cyclic minimum of
$T_2 \ni b$
. Let c be the cyclic minimum of
![]() $T_1$
and d the cyclic minimum of
$T_1$
and d the cyclic minimum of
![]() $T_2$
. It follows from the discussion in the proof of Lemma 8.18 that
$T_2$
. It follows from the discussion in the proof of Lemma 8.18 that
![]() $T^{\prime }_v$
has a directed edge from
$T^{\prime }_v$
has a directed edge from
![]() $c'$
to
$c'$
to
![]() $d'$
. One can check that
$d'$
. One can check that
![]() $c' \to d'$
intersects only
$c' \to d'$
intersects only
![]() $a \to b$
, and that the four vertices are in the stated order.
$a \to b$
, and that the four vertices are in the stated order.
Let
![]() $h_P(t)$
denote the h-polynomial of a simple d-dimensional polytope P. It is given by the equality
$h_P(t)$
denote the h-polynomial of a simple d-dimensional polytope P. It is given by the equality
![]() $\sum _{i=0}^d f_i(P) t^i = h_P(t+1)$
.
$\sum _{i=0}^d f_i(P) t^i = h_P(t+1)$
.
Corollary 8.20. Suppose P is a generic simple polypositroid. The h-polynomial of P is
 $$ \begin{align*}h_P(t) = \sum_{T^{\prime}_v \in {\mathcal{T}}(P)} t^{\mathrm{des}(T^{\prime}_v)} = \sum_{T_v \in {\mathcal{T}}(P)} t^{\mathrm{up}(T_v)}. \end{align*} $$
$$ \begin{align*}h_P(t) = \sum_{T^{\prime}_v \in {\mathcal{T}}(P)} t^{\mathrm{des}(T^{\prime}_v)} = \sum_{T_v \in {\mathcal{T}}(P)} t^{\mathrm{up}(T_v)}. \end{align*} $$
Proof. The first equality is shown in [Reference Postnikov, Reiner and WilliamsPRW, Theorem 4.2], and the second follows from Proposition 8.17, or it can be proved in the same way as the first.
Remark 8.21. The bijection of Theorem 8.19 gives a bijection between noncrossing, decreasing, alternating trees on
![]() $[n]$
, and rooted plane binary trees on
$[n]$
, and rooted plane binary trees on
![]() $[n]$
equipped with the depth-first search labeling.
$[n]$
equipped with the depth-first search labeling.
8.5. Coarsenings of braid arrangements
Recall that the braid arrangement
![]() ${\mathcal B}_n \subset (\mathbb {R}^n)^*/h_n$
is the central arrangement which is the union of all hyperplanes of the form
${\mathcal B}_n \subset (\mathbb {R}^n)^*/h_n$
is the central arrangement which is the union of all hyperplanes of the form
![]() $y_i - y_j = 0$
,
$y_i - y_j = 0$
,
![]() $i \neq j \in [n]$
, where
$i \neq j \in [n]$
, where
![]() $y = (y_1,y_2,\ldots ,y_n)$
is identified with the linear function
$y = (y_1,y_2,\ldots ,y_n)$
is identified with the linear function
![]() $y_1x_1 + y_2x_2 + \cdots + y_n x_n \in (\mathbb {R}^n)^*$
. We shall consider the hyperplane arrangement
$y_1x_1 + y_2x_2 + \cdots + y_n x_n \in (\mathbb {R}^n)^*$
. We shall consider the hyperplane arrangement
![]() ${\mathcal B}_n$
as a complete fan, the braid fan. The maximal cones of
${\mathcal B}_n$
as a complete fan, the braid fan. The maximal cones of
![]() ${\mathcal B}_n$
are indexed by
${\mathcal B}_n$
are indexed by
![]() $w \in S_n$
:
$w \in S_n$
:
and the rays of
![]() ${\mathcal B}_n$
are the
${\mathcal B}_n$
are the
![]() $h_S= \sum _{i \in S} x_i \in (\mathbb {R}^n)^*/h_n$
for
$h_S= \sum _{i \in S} x_i \in (\mathbb {R}^n)^*/h_n$
for
![]() $S \in 2^{[n]}-\{\emptyset ,[n]\}$
.
$S \in 2^{[n]}-\{\emptyset ,[n]\}$
.
The normal fan to the permutohedron
![]() $P_n \subset H$
is the braid fan
$P_n \subset H$
is the braid fan
![]() ${\mathcal B}_n$
. More generally, any generalized permutohedron P that is sufficiently generic has
${\mathcal B}_n$
. More generally, any generalized permutohedron P that is sufficiently generic has
![]() ${\mathcal B}_n$
as its normal fan (see [Reference Postnikov, Reiner and WilliamsPRW, Proposition 3.2]).
${\mathcal B}_n$
as its normal fan (see [Reference Postnikov, Reiner and WilliamsPRW, Proposition 3.2]).
Now, let P be a generic simple polypositroid and
![]() ${\mathcal F} = {\mathcal F}(P) \subset (\mathbb {R}^n)^*/h_n$
be its normal fan. The rays of
${\mathcal F} = {\mathcal F}(P) \subset (\mathbb {R}^n)^*/h_n$
be its normal fan. The rays of
![]() ${\mathcal F}$
are the
${\mathcal F}$
are the
![]() $h_{[r,s]}$
,
$h_{[r,s]}$
,
![]() $[r,s] \in \mathcal {I}$
. While there are many possibilities for
$[r,s] \in \mathcal {I}$
. While there are many possibilities for
![]() ${\mathcal F}$
, as we saw in Theorem 8.1, all such
${\mathcal F}$
, as we saw in Theorem 8.1, all such
![]() ${\mathcal F}$
have the same f-vector. By definition, P is a generalized permutohedron, so
${\mathcal F}$
have the same f-vector. By definition, P is a generalized permutohedron, so
![]() ${\mathcal F}$
is a coarsening of the fan
${\mathcal F}$
is a coarsening of the fan
![]() ${\mathcal B}_n$
. In particular, each maximal cone
${\mathcal B}_n$
. In particular, each maximal cone
![]() $C_T$
,
$C_T$
,
![]() $T \in {\mathcal {T}}(P)$
in
$T \in {\mathcal {T}}(P)$
in
![]() ${\mathcal F}$
is a union of a number of the cones
${\mathcal F}$
is a union of a number of the cones
![]() $C_w$
.
$C_w$
.
Proposition 8.22. Let
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
and
$T \in {\mathcal {T}}_{\mathrm {alt}}$
and
![]() $w \in S_n$
. We have
$w \in S_n$
. We have
![]() $C_w \subset C_T$
if and only if for each edge
$C_w \subset C_T$
if and only if for each edge
![]() $j \to i$
of
$j \to i$
of
![]() $T' = \varphi (T)$
, we have
$T' = \varphi (T)$
, we have
![]() $w^{-1}(i)> w^{-1}(j)$
.
$w^{-1}(i)> w^{-1}(j)$
.
Proof. By Proposition 8.15, the inclusion
![]() $C_w \subset C_T$
is equivalent to the condition that for all
$C_w \subset C_T$
is equivalent to the condition that for all
![]() $y \in C_w$
and
$y \in C_w$
and
![]() $x \in C^{\prime }_{T'}$
we have
$x \in C^{\prime }_{T'}$
we have
![]() $y(x) \geq 0$
. This is equivalent to the condition that
$y(x) \geq 0$
. This is equivalent to the condition that
![]() $y(e_i - e_j) = y_i - y_j \geq 0$
for edges
$y(e_i - e_j) = y_i - y_j \geq 0$
for edges
![]() $j\to i$
of
$j\to i$
of
![]() $T'$
.
$T'$
.
Corollary 8.23. Let
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
. We have
$T \in {\mathcal {T}}_{\mathrm {alt}}$
. We have
![]() $C_T = C_w$
for some
$C_T = C_w$
for some
![]() $w \in S_n$
if and only if
$w \in S_n$
if and only if
![]() $\varphi (T) \in {\mathcal {T}}_{\mathrm {cir}}$
is a path. Furthermore, for such T, we have
$\varphi (T) \in {\mathcal {T}}_{\mathrm {cir}}$
is a path. Furthermore, for such T, we have
![]() $T \in {\mathcal {T}}(P)$
for any generic simple polypositroid.
$T \in {\mathcal {T}}(P)$
for any generic simple polypositroid.
Proof. Let
![]() $T' \in {\mathcal {T}}_{\mathrm {cir}}$
. If the underlying graph of
$T' \in {\mathcal {T}}_{\mathrm {cir}}$
. If the underlying graph of
![]() $T'$
is a path, then
$T'$
is a path, then
![]() $T'$
itself is a directed path. In such a case, the condition of Proposition 8.22 uniquely determines
$T'$
itself is a directed path. In such a case, the condition of Proposition 8.22 uniquely determines
![]() $w \in S_n$
, and conversely, w being uniquely determined implies that
$w \in S_n$
, and conversely, w being uniquely determined implies that
![]() $T'$
is a directed path. The last sentence follows from Theorem 8.4: the sources (respectively, the sinks) of T form cyclic intervals when
$T'$
is a directed path. The last sentence follows from Theorem 8.4: the sources (respectively, the sinks) of T form cyclic intervals when
![]() $T'$
is a path.
$T'$
is a path.
Example 8.24. Let
![]() $n =3$
. In this case, the normal fan of a generic simple polypositroid is the braid arrangement. There are six trees in
$n =3$
. In this case, the normal fan of a generic simple polypositroid is the braid arrangement. There are six trees in
![]() ${\mathcal {T}}_{\mathrm {alt}}$
:
${\mathcal {T}}_{\mathrm {alt}}$
:
and six in
![]() ${\mathcal {T}}_{\mathrm {cir}}$
:
${\mathcal {T}}_{\mathrm {cir}}$
:
Since the underlying graph of every
![]() $T' \in {\mathcal {T}}_{\mathrm {cir}}$
is a path, there is a unique
$T' \in {\mathcal {T}}_{\mathrm {cir}}$
is a path, there is a unique
![]() $w = w_{T'} \in S_n$
satisfying the condition of Proposition 8.22. This gives a bijection between
$w = w_{T'} \in S_n$
satisfying the condition of Proposition 8.22. This gives a bijection between
![]() ${\mathcal {T}}_{\mathrm {alt}}$
and
${\mathcal {T}}_{\mathrm {alt}}$
and
![]() $S_n$
, identifying
$S_n$
, identifying
![]() $C_T$
,
$C_T$
,
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
, and
$T \in {\mathcal {T}}_{\mathrm {alt}}$
, and
![]() $C_w$
,
$C_w$
,
![]() $w \in S_n$
.
$w \in S_n$
.
Example 8.25. Let
![]() $n = 4$
. We have
$n = 4$
. We have
![]() $|{\mathcal {T}}_{\mathrm {alt}}|=24$
, consisting of
$|{\mathcal {T}}_{\mathrm {alt}}|=24$
, consisting of
![]() $8$
trees that are stars and 16 trees that are paths. For a generic simple polypositroid P, we have
$8$
trees that are stars and 16 trees that are paths. For a generic simple polypositroid P, we have
![]() $|{\mathcal {T}}(P)| = f_0(P) = \binom {6}{3} = 20$
by Theorem 8.1. There are 16 trees in
$|{\mathcal {T}}(P)| = f_0(P) = \binom {6}{3} = 20$
by Theorem 8.1. There are 16 trees in
![]() $T \in {\mathcal {T}}_{\mathrm {alt}}$
, such that
$T \in {\mathcal {T}}_{\mathrm {alt}}$
, such that
![]() $\varphi (T)$
is a directed path. By Corollary 8.23, these trees belong to
$\varphi (T)$
is a directed path. By Corollary 8.23, these trees belong to
![]() ${\mathcal {T}}(P)$
, for any P.
${\mathcal {T}}(P)$
, for any P.
There are eight trees in
![]() ${\mathcal {T}}_{\mathrm {alt}}$
, such that
${\mathcal {T}}_{\mathrm {alt}}$
, such that
![]() $\varphi (T)$
is a (circular-alternating) star. These eight trees are the four cyclic rotations of the following two trees
$\varphi (T)$
is a (circular-alternating) star. These eight trees are the four cyclic rotations of the following two trees
For each of these trees,
![]() $C_T$
is a union of two of the cones
$C_T$
is a union of two of the cones
![]() $C_w$
. For example, take
$C_w$
. For example, take
![]() $T = (2 \to 1 \leftarrow 4 \to 3)$
with dual tree
$T = (2 \to 1 \leftarrow 4 \to 3)$
with dual tree
![]() $T' = (2,4 \to 3 \to 1)$
. According to Proposition 8.22, we have
$T' = (2,4 \to 3 \to 1)$
. According to Proposition 8.22, we have
![]() $C_{2 \to 1 \leftarrow 4 \to 3} = C_{2431} \cup C_{4231}$
. Similarly, we obtain
$C_{2 \to 1 \leftarrow 4 \to 3} = C_{2431} \cup C_{4231}$
. Similarly, we obtain
Thus, we have
Each
![]() ${\mathcal {T}}(P)$
contains either both
${\mathcal {T}}(P)$
contains either both
![]() $(2 \to 1 \leftarrow 4 \to 3)$
and
$(2 \to 1 \leftarrow 4 \to 3)$
and
![]() $(4\to 3 \leftarrow 2 \to 1)$
or both
$(4\to 3 \leftarrow 2 \to 1)$
or both
![]() $(4\to 1 \leftarrow 2 \to 3)$
and
$(4\to 1 \leftarrow 2 \to 3)$
and
![]() $(2\to 3 \leftarrow 4 \to 1)$
. Switching between these two choices corresponds to switching the matching
$(2\to 3 \leftarrow 4 \to 1)$
. Switching between these two choices corresponds to switching the matching
![]() $M_{\{2.4\},\{1,3\}}$
in
$M_{\{2.4\},\{1,3\}}$
in
![]() ${\mathcal {E}}(P)$
.
${\mathcal {E}}(P)$
.
9. Integer points in polypositroids
We assume in this section that
![]() $H = \{x \in \mathbb {R}^n \mid x_1+x_2+ \cdots + x_n = k\}$
, where k is an integer. A polytope
$H = \{x \in \mathbb {R}^n \mid x_1+x_2+ \cdots + x_n = k\}$
, where k is an integer. A polytope
![]() $P \subset H$
is an integer polytope if its vertices have integer coordinates. By translating P and H, we may and will assume that
$P \subset H$
is an integer polytope if its vertices have integer coordinates. By translating P and H, we may and will assume that
![]() $S := P \cap \mathbb {Z}^n \subset \mathbb {N}^n$
, so that to each integer point
$S := P \cap \mathbb {Z}^n \subset \mathbb {N}^n$
, so that to each integer point
![]() $p = (p_1,p_2,\ldots ,p_n) \in P$
, one may associate a multiset
$p = (p_1,p_2,\ldots ,p_n) \in P$
, one may associate a multiset
![]() $I_p$
of size k which contains
$I_p$
of size k which contains
![]() $p_1$
1’s,
$p_1$
1’s,
![]() $p_2$
2’s, and so on. Thus, if P is the matroid polytope of a matroid M, then the multisets
$p_2$
2’s, and so on. Thus, if P is the matroid polytope of a matroid M, then the multisets
![]() $I_p$
are honest sets, equal to the bases of M.
$I_p$
are honest sets, equal to the bases of M.
If
![]() $I = \{i_1\leq i_2 \leq \cdots \leq i_k\}$
and
$I = \{i_1\leq i_2 \leq \cdots \leq i_k\}$
and
![]() $J = \{j_1 \leq j_2 \leq \cdots \leq j_k\}$
are two multisets consisting of elements in
$J = \{j_1 \leq j_2 \leq \cdots \leq j_k\}$
are two multisets consisting of elements in
![]() $\{1,2,\ldots ,n\}$
, we define two multisets
$\{1,2,\ldots ,n\}$
, we define two multisets
![]() $\mathrm {sort}_1(I,J)$
and
$\mathrm {sort}_1(I,J)$
and
![]() $\mathrm {sort}_2(I,J)$
of the same size as follows. Let
$\mathrm {sort}_2(I,J)$
of the same size as follows. Let
![]() $I \cup J = \{a_1 \leq a_2 \leq \cdots \leq a_{2k}\}$
. Then
$I \cup J = \{a_1 \leq a_2 \leq \cdots \leq a_{2k}\}$
. Then
![]() $\mathrm {sort}_1(I,J) := \{a_1,a_3,\ldots ,a_{2k-1}\}$
and
$\mathrm {sort}_1(I,J) := \{a_1,a_3,\ldots ,a_{2k-1}\}$
and
![]() $\mathrm {sort}_2(I,J) := \{a_2,a_4,\ldots ,a_{2k}\}$
. For example, suppose
$\mathrm {sort}_2(I,J) := \{a_2,a_4,\ldots ,a_{2k}\}$
. For example, suppose
![]() $I = \{1,1,3,4,4,5\}$
and
$I = \{1,1,3,4,4,5\}$
and
![]() $J = \{1,2,2,2,3,4\}$
. Then
$J = \{1,2,2,2,3,4\}$
. Then
![]() $\mathrm {sort}_1(I,J) = \{1,1,2,3,4,4\}$
and
$\mathrm {sort}_1(I,J) = \{1,1,2,3,4,4\}$
and
![]() $\mathrm {sort}_2(I,J)=\{1,2,2,3,4,5\}$
.
$\mathrm {sort}_2(I,J)=\{1,2,2,3,4,5\}$
.
The following characterization of integer alcoved polytopes is given in [Reference Lam and PostnikovLP07].
Theorem 9.1 [Reference Lam and PostnikovLP07, Theorem 3.1]
Suppose
![]() $P \subset H$
is an integer polytope, such that
$P \subset H$
is an integer polytope, such that
![]() $S:= P \cap \mathbb {Z}^n \subset \mathbb {N}^n$
. Then P is an alcoved polytope if and only if for any
$S:= P \cap \mathbb {Z}^n \subset \mathbb {N}^n$
. Then P is an alcoved polytope if and only if for any
![]() $p,p' \in S$
, there exist
$p,p' \in S$
, there exist
![]() $q,q' \in S$
so that
$q,q' \in S$
so that
![]() $I_q = \mathrm {sort}_1(I_p,I_{p'})$
and
$I_q = \mathrm {sort}_1(I_p,I_{p'})$
and
![]() $I_{q'}=\mathrm {sort}_2(I_p,I_{p'})$
.
$I_{q'}=\mathrm {sort}_2(I_p,I_{p'})$
.
If a collection S of nonnegative integer points satisfies the condition in Theorem 9.1, then we call S sort-closed.
Murota [Reference MurotaMur] studies certain collections of lattice points called M-convex sets, which are essentially equivalent to the discrete polymatroids of Herzog and Hibi [Reference Herzog and HibiHH]. We use the terminology of the latter. A base polymatroid is a generalized permutohedron P, such that all the values
![]() $f_P(S)$
of the support function are nonnegative (see, for example [Reference Castillo and LiuCL, Section 3]). Any generalized permutohedron can be translated so that the nonnegativity condition holds. A discrete (base) polymatroid is a collection of multisubsets of
$f_P(S)$
of the support function are nonnegative (see, for example [Reference Castillo and LiuCL, Section 3]). Any generalized permutohedron can be translated so that the nonnegativity condition holds. A discrete (base) polymatroid is a collection of multisubsets of
![]() $[n]= \{1,2,\ldots ,n\}$
satisfying an exchange criterion. The exchange criterion can be formulated in the language of generalized permutohedra as follows.
$[n]= \{1,2,\ldots ,n\}$
satisfying an exchange criterion. The exchange criterion can be formulated in the language of generalized permutohedra as follows.
Theorem 9.2 [Reference Herzog and HibiHH, Theorem 2.3]
Suppose
![]() $P \subset H$
is an integer polytope. Let
$P \subset H$
is an integer polytope. Let
![]() $S:= P \cap \mathbb {Z}^n$
. Then P is a generalized permutohedron if and only if for any
$S:= P \cap \mathbb {Z}^n$
. Then P is a generalized permutohedron if and only if for any
![]() $p, q \in S$
, we have:
$p, q \in S$
, we have:
whenever
![]() $p_i> q_i$
, we can find j, so that
$p_i> q_i$
, we can find j, so that
![]() $p_j < q_j$
and
$p_j < q_j$
and
![]() $p_i -e_i+e_j \in S$
.
$p_i -e_i+e_j \in S$
.
If a collection S of integer points satisfies the condition in Theorem 9.2, we say S satisfies the Exchange Lemma. Combining Theorems 9.1 and 9.2, we obtain the following characterization of integer polypositroids:
Theorem 9.3. Suppose
![]() $P \subset H$
is an integer polytope, such that
$P \subset H$
is an integer polytope, such that
![]() $S:= P \cap \mathbb {Z}^n \subset \mathbb {N}^n$
. Then P is an integer polypositroid if and only if S is sort-closed, and S satisfies the Exchange Lemma.
$S:= P \cap \mathbb {Z}^n \subset \mathbb {N}^n$
. Then P is an integer polypositroid if and only if S is sort-closed, and S satisfies the Exchange Lemma.
Example 9.4. Let
![]() $P = P(\mathbf {v})$
for the Coxeter necklace
$P = P(\mathbf {v})$
for the Coxeter necklace
![]() $\mathbf {v}$
of Example 6.11. Then the set
$\mathbf {v}$
of Example 6.11. Then the set
![]() $S:= P\cap \mathbb {Z}^4$
consists of the integer vectors
$S:= P\cap \mathbb {Z}^4$
consists of the integer vectors
![]() $(p_1,p_2,p_3,p_4)$
satisfying
$(p_1,p_2,p_3,p_4)$
satisfying
![]() $0 \leq p_i \leq 3$
and
$0 \leq p_i \leq 3$
and
![]() $1 \leq p_i + p_{i+1} \leq 5$
, with indices taken modulo
$1 \leq p_i + p_{i+1} \leq 5$
, with indices taken modulo
![]() $4$
. In particular, the integer points
$4$
. In particular, the integer points
![]() $(3,0,3,0)$
and
$(3,0,3,0)$
and
![]() $(0,3,0,3)$
belong to S. If we removed these two integer points from S, the Exchange Lemma would still be satisfied. However, S would not be sort-closed, for example, by considering
$(0,3,0,3)$
belong to S. If we removed these two integer points from S, the Exchange Lemma would still be satisfied. However, S would not be sort-closed, for example, by considering
![]() $p = (3,1,2,0)$
and
$p = (3,1,2,0)$
and
![]() $q=(2,0,3,1)$
.
$q=(2,0,3,1)$
.
In the case that P consists of
![]() $0$
-
$0$
-
![]() $1$
vectors, Theorem 9.3 characterizes positroids as those collections
$1$
vectors, Theorem 9.3 characterizes positroids as those collections
![]() $M \subset \binom {[n]}{k}$
of k-element subsets that are both sort-closed and satisfies the Exchange Lemma.
$M \subset \binom {[n]}{k}$
of k-element subsets that are both sort-closed and satisfies the Exchange Lemma.
Corollary 9.5. Positroids are exactly the sort-closed matroids.
Remark 9.6. Corollary 9.5 can also be deduced directly from the characterization of positroids as matroids associated to points
![]() $X \in \mathrm {Gr}(k,n)_{\geq 0}$
in the totally nonnegative Grassmannian. Namely, the Plücker coordinates
$X \in \mathrm {Gr}(k,n)_{\geq 0}$
in the totally nonnegative Grassmannian. Namely, the Plücker coordinates
![]() $\Delta _I(X)$
of such a point satisfy inequalities that give a sort-closed matroid (see [Reference LamLam, Proposition 8.7]).
$\Delta _I(X)$
of such a point satisfy inequalities that give a sort-closed matroid (see [Reference LamLam, Proposition 8.7]).
Part II Coxeter polypositroids
Generalized permutohedra are defined by specifying the possible directions of edges. Alcoved polytopes are defined by specifying the possible directions of normal vectors to facets. The set of allowed edge directions and the set of allowed facet normal directions are related by the linear transformation
![]() $e_i \mapsto h_i$
. We give this linear transformation a root-system theoretic interpretation, and develop the theory of Coxeter polypositroids.
$e_i \mapsto h_i$
. We give this linear transformation a root-system theoretic interpretation, and develop the theory of Coxeter polypositroids.
10. Coxeter elements
10.1. Root systems
First, we recall some terminology and a few well-known facts related to root systems and Weyl groups (see [Reference BourbakiBou, Reference HumphreysHum] for more details).
Let
![]() $V\simeq \mathbb {R}^r$
be a vector space of dimension
$V\simeq \mathbb {R}^r$
be a vector space of dimension
![]() $r \geq 2$
equipped with a symmetric positive definite bilinear form
$r \geq 2$
equipped with a symmetric positive definite bilinear form
![]() $(x,y)$
. Let
$(x,y)$
. Let
![]() $R\subset V$
be an irreducible and reduced crystallographic root system of rank r. For a root
$R\subset V$
be an irreducible and reduced crystallographic root system of rank r. For a root
![]() $\alpha \in R$
, the corresponding coroot is
$\alpha \in R$
, the corresponding coroot is
![]() $\alpha ^{\vee } = 2\alpha /(\alpha ,\alpha )$
, and the reflection
$\alpha ^{\vee } = 2\alpha /(\alpha ,\alpha )$
, and the reflection
![]() $s_{\alpha }\in GL(V)$
with respect to
$s_{\alpha }\in GL(V)$
with respect to
![]() $\alpha $
is given by
$\alpha $
is given by
The Weyl group
![]() $W\subset GL(V)$
is the group generated by the reflections
$W\subset GL(V)$
is the group generated by the reflections
![]() $s_{\alpha }$
,
$s_{\alpha }$
,
![]() $\alpha \in R$
. Let us fix a choice of positive roots
$\alpha \in R$
. Let us fix a choice of positive roots
![]() $R^+\subset R$
and the corresponding choice of simple roots
$R^+\subset R$
and the corresponding choice of simple roots
![]() $\alpha _1,\dots ,\alpha _r$
in R and simple coroots
$\alpha _1,\dots ,\alpha _r$
in R and simple coroots
![]() $\alpha _1^{\vee },\ldots ,\alpha _r^{\vee }$
. The Cartan matrix
$\alpha _1^{\vee },\ldots ,\alpha _r^{\vee }$
. The Cartan matrix
![]() $A = (A_{ij})$
is given by
$A = (A_{ij})$
is given by
Let
![]() $s_i = s_{\alpha _i}$
be the simple reflections. It is well-known that all possible choices of positive roots are conjugate to each other by the action of the Weyl group W.
$s_i = s_{\alpha _i}$
be the simple reflections. It is well-known that all possible choices of positive roots are conjugate to each other by the action of the Weyl group W.
Let
![]() $\omega _1,\dots ,\omega _r\in V$
be the basis of V dual to the basis of simple coroots
$\omega _1,\dots ,\omega _r\in V$
be the basis of V dual to the basis of simple coroots
![]() $\alpha _1^{\vee },\dots , \alpha _r^{\vee }$
, that is,
$\alpha _1^{\vee },\dots , \alpha _r^{\vee }$
, that is,
![]() $(\alpha _j^{\vee },\omega _i)=\delta _{ij}$
for any
$(\alpha _j^{\vee },\omega _i)=\delta _{ij}$
for any
![]() $i,j\in \{1,\dots ,r\}$
. The vectors
$i,j\in \{1,\dots ,r\}$
. The vectors
![]() $\omega _1,\dots ,\omega _r$
are called fundamental weights. Let
$\omega _1,\dots ,\omega _r$
are called fundamental weights. Let
![]() $\Lambda \subset V$
denote the weight lattice spanned by
$\Lambda \subset V$
denote the weight lattice spanned by
![]() $\omega _1,\dots ,\omega _r$
.
$\omega _1,\dots ,\omega _r$
.
Remark 10.1. Many of our results hold even for noncrystallographic root systems. However, for the connections to cluster algebras in Section 18, we must use a crystallographic root system.
10.2. Coxeter elements
A standard Coxeter element
![]() $c=s_{i_1} s_{i_2}\cdots s_{i_r} \in W$
is the product of the simple reflections
$c=s_{i_1} s_{i_2}\cdots s_{i_r} \in W$
is the product of the simple reflections
![]() $s_1,\dots ,s_r$
written in some order
$s_1,\dots ,s_r$
written in some order
![]() $s_{i_1},\dots ,s_{i_r}$
. More generally, a Coxeter element
$s_{i_1},\dots ,s_{i_r}$
. More generally, a Coxeter element
![]() $c'= s_{i_1}'s_{i_2}'\cdots s_{i_r}'\in W$
is a similar product for some (possibly different) choice of simple reflections
$c'= s_{i_1}'s_{i_2}'\cdots s_{i_r}'\in W$
is a similar product for some (possibly different) choice of simple reflections
![]() $s_1',\dots ,s_r'$
. In other words, Coxeter elements are Weyl group conjugates
$s_1',\dots ,s_r'$
. In other words, Coxeter elements are Weyl group conjugates
![]() $c'=wcw^{-1}$
,
$c'=wcw^{-1}$
,
![]() $w\in W$
, of standard Coxeter elements c. Moreover, any two Coxeter elements are conjugates of each other. Thus, all Coxeter elements have the same order, called the Coxeter number h.
$w\in W$
, of standard Coxeter elements c. Moreover, any two Coxeter elements are conjugates of each other. Thus, all Coxeter elements have the same order, called the Coxeter number h.
The eigenvalues of a Coxeter element are
![]() $e^{2\pi \sqrt {-1}\, m_i /h}$
, where
$e^{2\pi \sqrt {-1}\, m_i /h}$
, where
![]() $m_1,\dots ,m_r\in \{1,\dots ,h-1\}$
are the exponents of the root system. In particular,
$m_1,\dots ,m_r\in \{1,\dots ,h-1\}$
are the exponents of the root system. In particular,
![]() $1$
is not an eigenvalue of c. This implies the following claim.
$1$
is not an eigenvalue of c. This implies the following claim.
Lemma 10.2. For any Coxeter element c, the transformation
![]() $I-c$
is an invertible element of
$I-c$
is an invertible element of
![]() $GL(V)$
, and the inverse is given by
$GL(V)$
, and the inverse is given by
![]() $ (I-c)^{-1} = -{1\over h} \sum _{j=1}^{h-1} j\, c^j$
.
$ (I-c)^{-1} = -{1\over h} \sum _{j=1}^{h-1} j\, c^j$
.
Proof. Since all eigenvalues of c are h-th roots of unity, not including the identity, we have
![]() $I+c+c^2+ \cdots + c^{h-1} = 0$
. Thus
$I+c+c^2+ \cdots + c^{h-1} = 0$
. Thus
 $$ \begin{align*} (I-c) ( \sum_{j=1}^{h-1} j\, c^j) =(\sum_{j=1}^{h-1} c^j) - (h-1)I = -hI.\\[-40pt] \end{align*} $$
$$ \begin{align*} (I-c) ( \sum_{j=1}^{h-1} j\, c^j) =(\sum_{j=1}^{h-1} c^j) - (h-1)I = -hI.\\[-40pt] \end{align*} $$
We say that a choice of positive roots
![]() $R^+$
is compatible with c if c is a standard Coxeter element with respect to
$R^+$
is compatible with c if c is a standard Coxeter element with respect to
![]() $R^+$
.
$R^+$
.
Let
![]() $\Gamma = \{1,c,c^2,\ldots ,c^{h-1}\} \subset W$
be the subgroup generated by c. Given
$\Gamma = \{1,c,c^2,\ldots ,c^{h-1}\} \subset W$
be the subgroup generated by c. Given
![]() $R^+$
compatible with c, and a reduced factorization
$R^+$
compatible with c, and a reduced factorization
![]() $c = s_1 s_2 \cdots s_r$
, we obtain a total ordering of the root system R: set
$c = s_1 s_2 \cdots s_r$
, we obtain a total ordering of the root system R: set
![]() $\beta _1 =\alpha _1$
,
$\beta _1 =\alpha _1$
,
![]() $\beta _2 = s_1 \alpha _2$
,
$\beta _2 = s_1 \alpha _2$
,
![]() $\ldots $
,
$\ldots $
,
![]() $\beta _r = s_1 s_2 \cdots s_{r-1} \alpha _r$
. Then define
$\beta _r = s_1 s_2 \cdots s_{r-1} \alpha _r$
. Then define
![]() $\beta _i$
for
$\beta _i$
for
![]() $i \in \mathbb {Z}$
recursively by
$i \in \mathbb {Z}$
recursively by
![]() $\beta _{i+r}:= c \beta _i$
. For each
$\beta _{i+r}:= c \beta _i$
. For each
![]() $i = 1,2,\ldots ,r$
, the roots
$i = 1,2,\ldots ,r$
, the roots
![]() $\beta _i, \beta _{i+r},\ldots ,\beta _{i+(h-1)r}$
is a
$\beta _i, \beta _{i+r},\ldots ,\beta _{i+(h-1)r}$
is a
![]() $\Gamma $
-orbit in R.
$\Gamma $
-orbit in R.
Proposition 10.3.
-
1. The set of
 $h \cdot r$
vectors
$h \cdot r$
vectors
 $ \{\beta _i \mid 1 \leq i \leq hr \}$
is exactly the set of all roots in R without repetitions. In particular,
$ \{\beta _i \mid 1 \leq i \leq hr \}$
is exactly the set of all roots in R without repetitions. In particular,
 $|R| = hr$
.
$|R| = hr$
. -
2. For each
 $i = 1,2,\ldots ,r$
, there exists a unique integer
$i = 1,2,\ldots ,r$
, there exists a unique integer
 $M(i) \in [1,h-1]$
, such that
$M(i) \in [1,h-1]$
, such that  $$ \begin{align*}\beta_{i}, c\beta_i, \ldots, c^{M(i)-1}\beta_i \in R^+, \text{ and } c^{M(i)} \beta_{i}, c^{M(i)+1} \beta_i, \ldots, c^{h-1}\beta_i \in R^-. \end{align*} $$
$$ \begin{align*}\beta_{i}, c\beta_i, \ldots, c^{M(i)-1}\beta_i \in R^+, \text{ and } c^{M(i)} \beta_{i}, c^{M(i)+1} \beta_i, \ldots, c^{h-1}\beta_i \in R^-. \end{align*} $$
Proof. Follows from [Reference BourbakiBou, Chapter VI, Section 1, n
![]() ${}^{\circ }$
11, Proposition 33].
${}^{\circ }$
11, Proposition 33].
The first part of the following result is [Reference Kirillov and ThindKiTh, Theorem 3.6]. It is stated there for simply-laced Weyl groups but holds in the multiply-laced types as well.
Proposition 10.4. Let
![]() $R_1^+$
and
$R_1^+$
and
![]() $R_2^+$
be two positive systems compatible with c. Then
$R_2^+$
be two positive systems compatible with c. Then
![]() $R_1^+$
and
$R_1^+$
and
![]() $R_2^+$
are related by a sequence of elementary transformations
$R_2^+$
are related by a sequence of elementary transformations
![]() $R^+ \mapsto (R^+)'$
of the following form: suppose
$R^+ \mapsto (R^+)'$
of the following form: suppose
![]() $s_i$
is a simple generator for
$s_i$
is a simple generator for
![]() $R^+$
and c has a reduced factorization either starting or ending in
$R^+$
and c has a reduced factorization either starting or ending in
![]() $s_i$
, then set
$s_i$
, then set
![]() $(R^+)' = s_i \cdot R^+$
.
$(R^+)' = s_i \cdot R^+$
.
If
![]() $c = s_1 \cdots s_r$
and
$c = s_1 \cdots s_r$
and
![]() $(R')^+ = s_1 R^+$
, then the total ordering of R coming from
$(R')^+ = s_1 R^+$
, then the total ordering of R coming from
![]() $((R')^+,c)$
is the cyclic shift
$((R')^+,c)$
is the cyclic shift
![]() $(\beta _2,\beta _3,\ldots ,\beta _{hr},\beta _1)$
.
$(\beta _2,\beta _3,\ldots ,\beta _{hr},\beta _1)$
.
For the remainder of this section, we fix a Coxeter element c and a choice of positive roots
![]() $R^+$
compatible with c. We extend the definition of the fundamental weights
$R^+$
compatible with c. We extend the definition of the fundamental weights
![]() $\omega _i$
by defining
$\omega _i$
by defining
![]() $\omega _i$
for
$\omega _i$
for
![]() $i \in \mathbb {Z}$
recursively by
$i \in \mathbb {Z}$
recursively by
![]() $\omega _{i+r}:= c\omega _i$
.
$\omega _{i+r}:= c\omega _i$
.
Proposition 10.5. We have
![]() $(I-c)\omega _i = \beta _i$
for all
$(I-c)\omega _i = \beta _i$
for all
![]() $i \in \mathbb {Z}$
.
$i \in \mathbb {Z}$
.
Proof. According to the definitions,
![]() $s_j(\omega _i) = \omega _i - \delta _{ij}\,\alpha _j$
. Repeatedly applying the simple reflections
$s_j(\omega _i) = \omega _i - \delta _{ij}\,\alpha _j$
. Repeatedly applying the simple reflections
![]() $s_r, s_{r-1},\dots ,s_1$
to
$s_r, s_{r-1},\dots ,s_1$
to
![]() $\omega _i$
, we get
$\omega _i$
, we get
![]() $c(\omega _i) = s_1\cdots s_r (\omega _i) = \omega _i - s_1\cdots s_{i-1}(\alpha _i)$
. Thus
$c(\omega _i) = s_1\cdots s_r (\omega _i) = \omega _i - s_1\cdots s_{i-1}(\alpha _i)$
. Thus
The statement now follows from Proposition 10.3.
For convenience, when
![]() $\beta \in R$
, we use the notation
$\beta \in R$
, we use the notation
![]() ${\tilde {\beta }}$
to denote
${\tilde {\beta }}$
to denote
![]() $(I-c)^{-1} \beta \in {\tilde R}$
. Thus,
$(I-c)^{-1} \beta \in {\tilde R}$
. Thus,
![]() $\omega _i = {\tilde {\beta }}_i$
for
$\omega _i = {\tilde {\beta }}_i$
for
![]() $i = 1,2,\ldots ,hr$
.
$i = 1,2,\ldots ,hr$
.
Let
![]() $w_0 \in W$
be the longest element, and let
$w_0 \in W$
be the longest element, and let
![]() $i \mapsto i^{\star }$
denote the bijection on
$i \mapsto i^{\star }$
denote the bijection on
![]() $\{1,2,\ldots ,r\}$
, determined by
$\{1,2,\ldots ,r\}$
, determined by
![]() $w_0 \alpha _i = - \alpha _{i^{\star }}$
. Recall that for
$w_0 \alpha _i = - \alpha _{i^{\star }}$
. Recall that for
![]() $i = 1,2,\ldots ,r$
, we have defined a positive integer
$i = 1,2,\ldots ,r$
, we have defined a positive integer
![]() $M(i)$
in Proposition 10.3.
$M(i)$
in Proposition 10.3.
Lemma 10.6. Fix
![]() $k \in I$
. We have
$k \in I$
. We have
-
1.
 $(c^m \beta ^{\vee }_i,\omega _k)\geq 0$
, for
$(c^m \beta ^{\vee }_i,\omega _k)\geq 0$
, for
 $0\leq m<M(k^{\star })$
and any
$0\leq m<M(k^{\star })$
and any
 $i=1,\dots ,r$
;
$i=1,\dots ,r$
; -
2.
 $(c^m \beta ^{\vee }_i,\omega _k) = 0$
, if
$(c^m \beta ^{\vee }_i,\omega _k) = 0$
, if
 $M(i) < M(k^{\star })$
and
$M(i) < M(k^{\star })$
and
 $M(i) \leq m<M(k^{\star })$
;
$M(i) \leq m<M(k^{\star })$
; -
3.
 $(c^m \beta ^{\vee }_i,\omega _k) = 0$
, if
$(c^m \beta ^{\vee }_i,\omega _k) = 0$
, if
 $M(k^{\star }) \leq M(i)$
and
$M(k^{\star }) \leq M(i)$
and
 $M(k^{\star }) \leq m < M(i)$
;
$M(k^{\star }) \leq m < M(i)$
; -
4.
 $(c^m \beta ^{\vee }_i,\omega _k)\leq 0$
, for
$(c^m \beta ^{\vee }_i,\omega _k)\leq 0$
, for
 $M(k^{\star })\leq m <h$
and any
$M(k^{\star })\leq m <h$
and any
 $i=1,\dots ,r$
.
$i=1,\dots ,r$
.
Define
![]() $i \prec _c j$
if i and j are connected in the Dynkin diagram, and
$i \prec _c j$
if i and j are connected in the Dynkin diagram, and
![]() $s_i$
precedes
$s_i$
precedes
![]() $s_j$
in c. Orient the Coxeter diagram of W so that an edge
$s_j$
in c. Orient the Coxeter diagram of W so that an edge
![]() $(i,j)$
is oriented
$(i,j)$
is oriented
![]() $j \to i$
if
$j \to i$
if
![]() $i \prec _c j$
. We will use the following formulae from [Reference Yang and ZelevinskyYZ].
$i \prec _c j$
. We will use the following formulae from [Reference Yang and ZelevinskyYZ].
Lemma 10.7. We have
-
1.
 $c^{M(i)}\beta _i = -\beta _{i^*}$
;
$c^{M(i)}\beta _i = -\beta _{i^*}$
; -
2.
 $M(i) + M(i^{\star }) = h$
;
$M(i) + M(i^{\star }) = h$
; -
3. If
 $j \to i$
, then we have
$j \to i$
, then we have  $$ \begin{align*}M(i) - M(j) =\begin{cases} 1 & \mbox{if } i^{\star} \to j^{\star} \\ 0 & \mbox{if } j^{\star} \to i^{\star} \end{cases}. \end{align*} $$
$$ \begin{align*}M(i) - M(j) =\begin{cases} 1 & \mbox{if } i^{\star} \to j^{\star} \\ 0 & \mbox{if } j^{\star} \to i^{\star} \end{cases}. \end{align*} $$
Proof of Lemma 10.6
Fix i and j. We prove
![]() $(c^m \beta ^{\vee }_i,\omega _j) \geq 0$
for
$(c^m \beta ^{\vee }_i,\omega _j) \geq 0$
for
![]() $0 \leq m < M(j^{\star })$
. If
$0 \leq m < M(j^{\star })$
. If
![]() $m < M(i)$
, then by definition,
$m < M(i)$
, then by definition,
![]() $c^m \beta _i \in R^+$
, so
$c^m \beta _i \in R^+$
, so
![]() $c^m \beta ^{\vee }_i \in (R^{\vee })^+$
, and the inequality is clear. Thus, we may assume that
$c^m \beta ^{\vee }_i \in (R^{\vee })^+$
, and the inequality is clear. Thus, we may assume that
![]() $M(i) < M(j^{\star })$
and
$M(i) < M(j^{\star })$
and
![]() $M(i) \leq m < M(j^{\star })$
. In particular, we are assuming that
$M(i) \leq m < M(j^{\star })$
. In particular, we are assuming that
![]() $i \neq j$
.
$i \neq j$
.
Define the support
![]() $S(\beta ^{\vee }) \subseteq I$
of a coroot
$S(\beta ^{\vee }) \subseteq I$
of a coroot
![]() $\beta ^{\vee } \in R^{\vee }$
to be the (positive or negative) simple coroots that occur in the expansion of
$\beta ^{\vee } \in R^{\vee }$
to be the (positive or negative) simple coroots that occur in the expansion of
![]() $\beta ^{\vee }$
into simple coroots. For a nonnegative integer a, let
$\beta ^{\vee }$
into simple coroots. For a nonnegative integer a, let
![]() $P_a(i) \subseteq I$
be the set of vertices
$P_a(i) \subseteq I$
be the set of vertices
![]() $j \in I$
that can be reached from
$j \in I$
that can be reached from
![]() $i \in I$
by a path where at most a edges are in the wrong direction. One can check that
$i \in I$
by a path where at most a edges are in the wrong direction. One can check that
and by induction on a, we have for
![]() $a \geq 0$
,
$a \geq 0$
,
By Lemma 10.7(1), it follows that we have
for
![]() $m \geq M(i)$
. But, by Lemma 10.7(3),
$m \geq M(i)$
. But, by Lemma 10.7(3),
![]() $M(j^{\star }) - M(i)$
is bounded above by the number of edges directed in the wrong direction on the path from
$M(j^{\star }) - M(i)$
is bounded above by the number of edges directed in the wrong direction on the path from
![]() $i^{\star }$
to j. Thus, if
$i^{\star }$
to j. Thus, if
![]() $m < M(j^{\star })$
, we have
$m < M(j^{\star })$
, we have
![]() $j \notin P_{m-M(i)}(i^{\star })$
and
$j \notin P_{m-M(i)}(i^{\star })$
and
![]() $(c^m \beta ^{\vee }_i,\omega _j) = 0 \geq 0$
. This proves statements (1) and (2). Statements (3) and (4) are similar.
$(c^m \beta ^{\vee }_i,\omega _j) = 0 \geq 0$
. This proves statements (1) and (2). Statements (3) and (4) are similar.
Example 10.8. We consider the root system of type
![]() $A_{n-1}$
. Let
$A_{n-1}$
. Let
![]() $V = H_0 = \{x \mid x_1+x_2+\cdots +x_n=0\} \subset \mathbb {R}^n$
and
$V = H_0 = \{x \mid x_1+x_2+\cdots +x_n=0\} \subset \mathbb {R}^n$
and
![]() $R = \{e_i - e_j \mid i \neq j\}$
. Then W is the symmetric group
$R = \{e_i - e_j \mid i \neq j\}$
. Then W is the symmetric group
![]() $S_n$
. We take as positive simple roots
$S_n$
. We take as positive simple roots
![]() $\alpha _i = e_{i+1}-e_i$
. Then the linear functional
$\alpha _i = e_{i+1}-e_i$
. Then the linear functional
![]() $(\cdot , \omega _k): V \to \mathbb {R}$
can be identified with the function
$(\cdot , \omega _k): V \to \mathbb {R}$
can be identified with the function
![]() $h_n - h_k \in (\mathbb {R}^n)^*$
.
$h_n - h_k \in (\mathbb {R}^n)^*$
.
Now choose the Coxeter element
![]() $c = s_1 s_2 \cdots s_{n-1}$
, which coincides with our choice in Section 5. The Dynkin diagram is oriented as follows:
$c = s_1 s_2 \cdots s_{n-1}$
, which coincides with our choice in Section 5. The Dynkin diagram is oriented as follows:
We have
![]() $\beta _i = s_1 \cdots s_{i-1} (e_{i+1}-e_r) = e_{i+1}-e_1$
for
$\beta _i = s_1 \cdots s_{i-1} (e_{i+1}-e_r) = e_{i+1}-e_1$
for
![]() $i=1,2,\ldots ,n-1$
. We have
$i=1,2,\ldots ,n-1$
. We have
![]() $c(e_i) = e_{i+1}$
, where
$c(e_i) = e_{i+1}$
, where
![]() $e_{n+1}:=e_1$
. We compute that
$e_{n+1}:=e_1$
. We compute that
![]() $i^{\star } = n-i = M(i)$
. It is straightforward to verify Lemma 10.6 directly, noting also that for
$i^{\star } = n-i = M(i)$
. It is straightforward to verify Lemma 10.6 directly, noting also that for
![]() $R= A_{n-1}$
, we have
$R= A_{n-1}$
, we have
![]() $\beta = \beta ^{\vee }$
.
$\beta = \beta ^{\vee }$
.
Example 10.9. We consider the root system of type
![]() $B_r$
with
$B_r$
with
![]() $V = \mathbb {R}^r$
and simple roots
$V = \mathbb {R}^r$
and simple roots
![]() $\alpha _1 = e_1 - e_2, \alpha _2 = e_2 - e_3, \ldots , \alpha _{r-1}=e_{r-1}-e_r, \alpha _r = e_r$
, and Coxeter element
$\alpha _1 = e_1 - e_2, \alpha _2 = e_2 - e_3, \ldots , \alpha _{r-1}=e_{r-1}-e_r, \alpha _r = e_r$
, and Coxeter element
![]() $c = s_1s_2\cdots s_r$
. Thus,
$c = s_1s_2\cdots s_r$
. Thus,
![]() $\beta _1 = e_1-e_2, \beta _2 = e_1-e_3, \ldots ,\beta _{r-1}=e_1-e_r, \beta _r = e_1$
. We have
$\beta _1 = e_1-e_2, \beta _2 = e_1-e_3, \ldots ,\beta _{r-1}=e_1-e_r, \beta _r = e_1$
. We have
![]() $c(e_1)=e_2, c(e_2) = e_3, \ldots $
, and
$c(e_1)=e_2, c(e_2) = e_3, \ldots $
, and
![]() $c(e_r) = -e_1$
. We have
$c(e_r) = -e_1$
. We have
![]() $M(i) = r$
for all i and
$M(i) = r$
for all i and
![]() $i^{\star } = i$
. Thus,
$i^{\star } = i$
. Thus,
![]() $M(i)+ M(i^{\star }) = 2r= h$
, the Coxeter number. Since all
$M(i)+ M(i^{\star }) = 2r= h$
, the Coxeter number. Since all
![]() $M(i) = r$
are equal, Lemma 10.6 follows immediately from
$M(i) = r$
are equal, Lemma 10.6 follows immediately from
![]() $c^m \beta _i^{\vee } \in (R^+)^{\vee }$
for
$c^m \beta _i^{\vee } \in (R^+)^{\vee }$
for
![]() $0 \leq m < r$
and
$0 \leq m < r$
and
![]() $c^m \beta _i^{\vee } \in (R^-)^{\vee }$
for
$c^m \beta _i^{\vee } \in (R^-)^{\vee }$
for
![]() $n \leq m < 2r=h$
.
$n \leq m < 2r=h$
.
11. Generalized W-permutohedra
A W-permutohedron P is a convex polytope in the space V which is the convex hull of an orbit
![]() $W(x)$
of the Weyl group W, for some
$W(x)$
of the Weyl group W, for some
![]() $x\in V$
not lying in any of the hyperplanes
$x\in V$
not lying in any of the hyperplanes
![]() $H_{\alpha } := \{x \in V \mid (x,\alpha ) = 0\}$
,
$H_{\alpha } := \{x \in V \mid (x,\alpha ) = 0\}$
,
![]() $\alpha \in R$
. One key property of W-permutohedra is that every edge of P is parallel to some coroot
$\alpha \in R$
. One key property of W-permutohedra is that every edge of P is parallel to some coroot
![]() $\alpha ^{\vee }\in R^{\vee }$
.
$\alpha ^{\vee }\in R^{\vee }$
.
Definition 11.1. A generalized W-permutohedron P is a convex polytope in the space V, such that every edge
![]() $[u,v]$
of P is parallel to a coroot
$[u,v]$
of P is parallel to a coroot
![]() $\alpha ^{\vee }\in R^{\vee }$
, that is,
$\alpha ^{\vee }\in R^{\vee }$
, that is,
![]() $u-v= a \alpha ^{\vee }$
, for some
$u-v= a \alpha ^{\vee }$
, for some
![]() $a\in \mathbb {R}_{> 0}$
.
$a\in \mathbb {R}_{> 0}$
.
Note that the notion of a generalized W-permutohedron is unchanged when we replace the root system R by the dual root system
![]() $R^{\vee }$
. Furthermore, the class of generalized W-permutohedra is preserved by the action of W.
$R^{\vee }$
. Furthermore, the class of generalized W-permutohedra is preserved by the action of W.
The normal fan to a W-permutohedron is the W-Coxeter fan, the fan associated to the hyperplane arrangement consisting of all hyperplanes
![]() $H_{\alpha }$
as
$H_{\alpha }$
as
![]() $\alpha \in R$
varies. The maximal cones of the W-Coxeter fan are indexed by
$\alpha \in R$
varies. The maximal cones of the W-Coxeter fan are indexed by
![]() $w \in W$
. The
$w \in W$
. The
![]() $1$
-dimensional cones, or rays, of the W-Coxeter fan are generated by the set
$1$
-dimensional cones, or rays, of the W-Coxeter fan are generated by the set
![]() $W \cdot \{\omega _1,\ldots ,\omega _r\}$
of vectors lying in the W-orbit of a fundamental weight. Generalized W-permutohedra can be equivalently defined as convex polytopes whose normal fan refines the W-Coxeter fan (see, for example [Reference Postnikov, Reiner and WilliamsPRW, Theorem 15.3]). In particular, any facet of a generalized W-permutohedron has a normal vector that lies in the W-orbit of a fundamental weight. Thus, a generalized W-permutohedron is given by a collection of inequalities
$W \cdot \{\omega _1,\ldots ,\omega _r\}$
of vectors lying in the W-orbit of a fundamental weight. Generalized W-permutohedra can be equivalently defined as convex polytopes whose normal fan refines the W-Coxeter fan (see, for example [Reference Postnikov, Reiner and WilliamsPRW, Theorem 15.3]). In particular, any facet of a generalized W-permutohedron has a normal vector that lies in the W-orbit of a fundamental weight. Thus, a generalized W-permutohedron is given by a collection of inequalities
where we always assume that
![]() $a_{\omega }$
has been taken minimal. Let
$a_{\omega }$
has been taken minimal. Let
![]() ${\mathcal {C}}_{\mathrm {sub}}^W = \{(a_{\omega })\}$
denote the cone of vectors
${\mathcal {C}}_{\mathrm {sub}}^W = \{(a_{\omega })\}$
denote the cone of vectors
![]() $(a_{\omega })$
arising from generalized W-permutohedra. This cone is studied in [Reference Ardila, Castillo, Eur and PostnikovACEP].
$(a_{\omega })$
arising from generalized W-permutohedra. This cone is studied in [Reference Ardila, Castillo, Eur and PostnikovACEP].
Let the dominant cone
be the cone of nonnegative linear combinations of the simple (equivalently, positive) roots in R. For example, with
![]() $R = A_{n-1}$
and the conventions of Example 10.8, this agrees with the cone (5.1), intersected with
$R = A_{n-1}$
and the conventions of Example 10.8, this agrees with the cone (5.1), intersected with
![]() $H_0 \simeq V$
. The cone C is the dual of the dominant Weyl chamber
$H_0 \simeq V$
. The cone C is the dual of the dominant Weyl chamber
![]() $D=\mathbb {R}_{\geq 0}\left <\omega _1,\dots ,\omega _r\right>$
. Namely,
$D=\mathbb {R}_{\geq 0}\left <\omega _1,\dots ,\omega _r\right>$
. Namely,
![]() $D=\{y\in V\mid (x,y)\geq 0\textrm { for any } x \in C\}$
and
$D=\{y\in V\mid (x,y)\geq 0\textrm { for any } x \in C\}$
and
![]() $C=\{x\in V\mid (x,y)\geq 0\textrm { for any } y \in D\}$
. The following result follows from the statement that the normal fan of a generalized W-permutohedra is a refinement of the W-Coxeter fan.
$C=\{x\in V\mid (x,y)\geq 0\textrm { for any } y \in D\}$
. The following result follows from the statement that the normal fan of a generalized W-permutohedra is a refinement of the W-Coxeter fan.
Theorem 11.2. A polytope P is a generalized W-permutohedron if and only if it has the following form
where
![]() $v_w\in V$
,
$v_w\in V$
,
![]() $w\in W$
, is a collection of points in V, such that, for any
$w\in W$
, is a collection of points in V, such that, for any
![]() $u, w\in W$
,
$u, w\in W$
,
The points
![]() $v_w, w\in W$
are exactly all vertices of the polytope P (possibly with repetitions).
$v_w, w\in W$
are exactly all vertices of the polytope P (possibly with repetitions).
Define the dominance order
![]() $\leq _C$
as the partial order on points V given by
$\leq _C$
as the partial order on points V given by
![]() $x\leq _C y$
if
$x\leq _C y$
if
![]() $y-x\in C$
. Similarly, for
$y-x\in C$
. Similarly, for
![]() $w\in W$
, the w-dominance order
$w\in W$
, the w-dominance order
![]() $\leq _{w(C)}$
is the partial order on V given by
$\leq _{w(C)}$
is the partial order on V given by
![]() $x\leq _{w(C)} y$
if
$x\leq _{w(C)} y$
if
![]() $y-x\in w(C)$
, for
$y-x\in w(C)$
, for
![]() $w\in W$
. The following result easily follows from Theorem 11.2.
$w\in W$
. The following result easily follows from Theorem 11.2.
Corollary 11.3. A polytope P is a generalized W-permutohedron if and only if for each
![]() $w\in W$
, P has a unique minimum element
$w\in W$
, P has a unique minimum element
![]() $v_w\in P$
in the w-dominance order
$v_w\in P$
in the w-dominance order
![]() $\leq _{w(C)}$
.
$\leq _{w(C)}$
.
[Reference Postnikov, Reiner and WilliamsPRW, Theorem 15.3] also implies that the condition on the points
![]() $v_w$
,
$v_w$
,
![]() $w\in W$
can be reformulated, as follows. It is enough to require the condition
$w\in W$
can be reformulated, as follows. It is enough to require the condition
![]() $v_u - v_w \in w(C)\cap (-u(C))$
only for the pairs
$v_u - v_w \in w(C)\cap (-u(C))$
only for the pairs
![]() $u,w\in W$
, such that
$u,w\in W$
, such that
![]() $u= w\, s_i$
, for a simple reflection
$u= w\, s_i$
, for a simple reflection
![]() $s_i$
. In this case, the cone
$s_i$
. In this case, the cone
![]() $w(C)\cap (-w \, s_i (C))$
is the
$w(C)\cap (-w \, s_i (C))$
is the
![]() $1$
-dimensional cone spanned by the coroot
$1$
-dimensional cone spanned by the coroot
![]() $w(\alpha ^{\vee }_i)$
:
$w(\alpha ^{\vee }_i)$
:
Theorem 11.4. A polytope P is a generalized W-permutohedron if and only if it has the following form
where
![]() $v_w\in V$
,
$v_w\in V$
,
![]() $w\in W$
is a collection of points in V, such that, for any
$w\in W$
is a collection of points in V, such that, for any
![]() $w\in W$
and
$w\in W$
and
![]() $i=1,\dots ,r$
,
$i=1,\dots ,r$
,
12. Twisted
 $(W,c)$
-alcoved polytopes
$(W,c)$
-alcoved polytopes
In [Reference Lam, Postnikov, Kac and PopovLP18], we studied the W-alcoved polytopes: polytopes in V with the property that all facet normals belong to R. Here, we introduce a twisted variant of W-alcoved polytopes that depends on the choice of a Coxeter element c.
12.1. Coxeter twisted roots
Definition 12.1. Define the c-twisted root system
![]() $\tilde R$
as the image
$\tilde R$
as the image
![]() $\tilde R = (I-c)^{-1}(R)$
of the root system R under the transformation
$\tilde R = (I-c)^{-1}(R)$
of the root system R under the transformation
![]() $(I-c)^{-1}$
. We call the elements of
$(I-c)^{-1}$
. We call the elements of
![]() $\tilde R$
the c-twisted roots, or simply twisted roots if the Coxeter element is understood.
$\tilde R$
the c-twisted roots, or simply twisted roots if the Coxeter element is understood.
We have that
![]() $\tilde R = -\tilde R$
. Note also that
$\tilde R = -\tilde R$
. Note also that
![]() $\tilde R$
does not depend on the choice of positive system
$\tilde R$
does not depend on the choice of positive system
![]() $R^+$
.
$R^+$
.
According to Lemma 10.5, the twisted root system
![]() $\tilde R$
is exactly the set of weights that lie in the
$\tilde R$
is exactly the set of weights that lie in the
![]() $\Gamma $
-orbits of the vectors
$\Gamma $
-orbits of the vectors
![]() $\omega _1,\omega _2,\ldots ,\omega _r$
:
$\omega _1,\omega _2,\ldots ,\omega _r$
:
Note that
![]() $\tilde R = \Gamma \cdot \{\omega _1,\ldots ,\omega _r\} \subset W \cdot \{\omega _1,\ldots ,\omega _r\}$
.
$\tilde R = \Gamma \cdot \{\omega _1,\ldots ,\omega _r\} \subset W \cdot \{\omega _1,\ldots ,\omega _r\}$
.
Definition 12.2. A
![]() $(W,c)$
-twisted alcoved polytope is a polytope
$(W,c)$
-twisted alcoved polytope is a polytope
![]() $P \subset V$
whose facets are normal to twisted roots. More precisely, P is a nonempty set with the presentation
$P \subset V$
whose facets are normal to twisted roots. More precisely, P is a nonempty set with the presentation
Here,
![]() $a_{\omega }$
are arbitrary real numbers which we always assume to be chosen minimal.
$a_{\omega }$
are arbitrary real numbers which we always assume to be chosen minimal.
Example 12.3. We continue Example 10.8. Applying Lemma 10.2, the twisted roots are given by
 $$ \begin{align*}{\tilde R}= \left\{-\frac{1}{n}\left(\sum_{k=1}^{n-1} k (e_{i+k}-e_{j+k}) \right) \mid i \neq j \right\} \subset V. \end{align*} $$
$$ \begin{align*}{\tilde R}= \left\{-\frac{1}{n}\left(\sum_{k=1}^{n-1} k (e_{i+k}-e_{j+k}) \right) \mid i \neq j \right\} \subset V. \end{align*} $$
For example,
![]() $(I-c)^{-1}\alpha _1 = \frac {1}{5}(-4,1,1,1,1)$
. In
$(I-c)^{-1}\alpha _1 = \frac {1}{5}(-4,1,1,1,1)$
. In
![]() $(\mathbb {R}^n)^*/h_n$
, this is equal to
$(\mathbb {R}^n)^*/h_n$
, this is equal to
![]() $h_n-h_1 =(0,1,1,1,1)$
. Identifying
$h_n-h_1 =(0,1,1,1,1)$
. Identifying
![]() ${\tilde R}$
with a subset of
${\tilde R}$
with a subset of
![]() $(\mathbb {R}^n)^*/h_n$
, we get
$(\mathbb {R}^n)^*/h_n$
, we get
![]() ${\tilde R} = \{h_i - h_j \mid i \neq j\}$
. The notion of
${\tilde R} = \{h_i - h_j \mid i \neq j\}$
. The notion of
![]() $(W,c)$
-twisted alcoved polytope here agrees with our notion of alcoved polytope in Definition 3.3.
$(W,c)$
-twisted alcoved polytope here agrees with our notion of alcoved polytope in Definition 3.3.
If W and c are understood to be fixed, we may simply use the name “twisted alcoved polytope.”
Remark 12.4. Suppose that c and
![]() $c'$
are two Coxeter elements. Then there exists
$c'$
are two Coxeter elements. Then there exists
![]() $w \in W$
so that
$w \in W$
so that
![]() $c' = wcw^{-1}$
. The c-twisted roots
$c' = wcw^{-1}$
. The c-twisted roots
![]() $\tilde R_c$
and the
$\tilde R_c$
and the
![]() $c'$
-twisted roots
$c'$
-twisted roots
![]() $\tilde R_{c'}$
are related by
$\tilde R_{c'}$
are related by
![]() $\tilde R_{c'} = w \cdot \tilde R_c$
. We have that
$\tilde R_{c'} = w \cdot \tilde R_c$
. We have that
![]() $P \subset V$
is a
$P \subset V$
is a
![]() $(W,c')$
-twisted alcoved polytope if and only if
$(W,c')$
-twisted alcoved polytope if and only if
![]() $w \cdot P \subset V$
is a
$w \cdot P \subset V$
is a
![]() $(W,c)$
-twisted alcoved polytope.
$(W,c)$
-twisted alcoved polytope.
Definition 12.5. For a compact subset
![]() $Q \subset V$
, the
$Q \subset V$
, the
![]() $(W,c)$
-twisted alcoved envelope
$(W,c)$
-twisted alcoved envelope
![]() $\mathrm {env}(Q)$
is the smallest
$\mathrm {env}(Q)$
is the smallest
![]() $(W,c)$
-twisted alcoved polytope containing Q.
$(W,c)$
-twisted alcoved polytope containing Q.
Clearly,
![]() $\mathrm {env}(P) = P$
if and only if P is a
$\mathrm {env}(P) = P$
if and only if P is a
![]() $(W,c)$
-twisted alcoved polytope. Note that the intersection of generalized W-permutohedra may not be a generalized W-permutohedron. Thus, the “generalized W-permutohedron envelope” is not a well-defined operation.
$(W,c)$
-twisted alcoved polytope. Note that the intersection of generalized W-permutohedra may not be a generalized W-permutohedron. Thus, the “generalized W-permutohedron envelope” is not a well-defined operation.
Recall that the dominant cone C was defined in (11.2). Let
![]() $Q \subset V$
be a compact subset. For
$Q \subset V$
be a compact subset. For
![]() $i = 0,1,\ldots ,h-1$
, let
$i = 0,1,\ldots ,h-1$
, let
![]() $v_i \in V$
be the minimum point in dominance order
$v_i \in V$
be the minimum point in dominance order
![]() $\leq _{c^i(C)}$
, such that
$\leq _{c^i(C)}$
, such that
![]() $Q \subset v_i + c^i(C)$
. Thus, every facet of
$Q \subset v_i + c^i(C)$
. Thus, every facet of
![]() $v_i+c^i(C)$
touches Q.
$v_i+c^i(C)$
touches Q.
Proposition 12.6. The
![]() $(W,c)$
-twisted alcoved envelope of Q is given by the following intersection:
$(W,c)$
-twisted alcoved envelope of Q is given by the following intersection:
 $$ \begin{align*}\mathrm{env}(Q) = \mathrm{env}_c(Q)= \bigcap_{i=0}^{h-1}( v_i + c^i(C)). \end{align*} $$
$$ \begin{align*}\mathrm{env}(Q) = \mathrm{env}_c(Q)= \bigcap_{i=0}^{h-1}( v_i + c^i(C)). \end{align*} $$
Proof. Since Q is compact, for each
![]() $\omega \in \tilde R$
, there is a minimal number
$\omega \in \tilde R$
, there is a minimal number
![]() $a_{\omega }$
, such that Q belongs to the half space
$a_{\omega }$
, such that Q belongs to the half space
![]() $H_{\omega }^+ := \{x \in V \mid (x,\omega ) \leq a_{\omega }\}$
. Then
$H_{\omega }^+ := \{x \in V \mid (x,\omega ) \leq a_{\omega }\}$
. Then
![]() $\mathrm {env}(Q) = \bigcap _{\omega \in \tilde R} H_{\omega }^+$
. The convex cone C has inward pointing normals given by
$\mathrm {env}(Q) = \bigcap _{\omega \in \tilde R} H_{\omega }^+$
. The convex cone C has inward pointing normals given by
![]() $\omega _1,\omega _2,\ldots ,\omega _r$
. Thus,
$\omega _1,\omega _2,\ldots ,\omega _r$
. Thus,
![]() $v_0 + C = \bigcap _{j=1}^r H_{-\omega _j}^+$
, and similarly, we have
$v_0 + C = \bigcap _{j=1}^r H_{-\omega _j}^+$
, and similarly, we have
![]() $v_i + c^i(C) = \bigcap _{j=1}^r H_{-c^i\omega _j}^+$
. The claim follows from (12.1) and the fact that
$v_i + c^i(C) = \bigcap _{j=1}^r H_{-c^i\omega _j}^+$
. The claim follows from (12.1) and the fact that
![]() ${\tilde R} = -{\tilde R}$
.
${\tilde R} = -{\tilde R}$
.
12.2. Faces of twisted alcoved polytopes
We call a
![]() $(W,c)$
-twisted alcoved polytope P generic if it is full-dimensional and every twisted root
$(W,c)$
-twisted alcoved polytope P generic if it is full-dimensional and every twisted root
![]() $\omega \in \tilde R$
defines a facet
$\omega \in \tilde R$
defines a facet
![]() $F = \{(x,\omega ) = a_{\omega }\} \cap P$
of P.
$F = \{(x,\omega ) = a_{\omega }\} \cap P$
of P.
Now let P be a
![]() $(W,c)$
-twisted alcoved polytope and F a face of P. Let
$(W,c)$
-twisted alcoved polytope and F a face of P. Let
![]() $S(F) \subset \tilde R$
be the set of twisted roots
$S(F) \subset \tilde R$
be the set of twisted roots
![]() $\omega $
, such that F lies on the hyperplane
$\omega $
, such that F lies on the hyperplane
![]() $(x,\omega ) = a_{\omega }$
and P lies in the halfspace
$(x,\omega ) = a_{\omega }$
and P lies in the halfspace
![]() $(x,\omega ) \leq a_{\omega }$
. The set
$(x,\omega ) \leq a_{\omega }$
. The set
![]() $S(F)$
is a
$S(F)$
is a
![]() $(W,c)$
-analogue of the graph
$(W,c)$
-analogue of the graph
![]() $T_F$
of Section 6.4.
$T_F$
of Section 6.4.
Suppose that
![]() $\beta $
and
$\beta $
and
![]() $\beta '$
are two distinct roots. We say that
$\beta '$
are two distinct roots. We say that
![]() $\beta $
and
$\beta $
and
![]() $\beta '$
are alternating if
$\beta '$
are alternating if
![]() $(\beta ,\beta ') \geq 0$
. Note that
$(\beta ,\beta ') \geq 0$
. Note that
![]() $\beta $
and
$\beta $
and
![]() $\beta '$
are alternating if and only if
$\beta '$
are alternating if and only if
![]() $-\beta $
and
$-\beta $
and
![]() $-\beta '$
are. Also note that this notion of alternating agrees with the notion used in the definition of alternating trees in Section 6.4. Suppose that
$-\beta '$
are. Also note that this notion of alternating agrees with the notion used in the definition of alternating trees in Section 6.4. Suppose that
![]() $\omega , \omega ' \in {\tilde R}$
are distinct twisted roots. Then we say that
$\omega , \omega ' \in {\tilde R}$
are distinct twisted roots. Then we say that
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
are alternating if
$\omega '$
are alternating if
![]() $(I-c)\omega $
and
$(I-c)\omega $
and
![]() $(I-c)\omega '$
are.
$(I-c)\omega '$
are.
Lemma 12.7. Suppose that P is a generic simple
![]() $(W,c)$
-twisted alcoved polytope and v a vertex of P. Then
$(W,c)$
-twisted alcoved polytope and v a vertex of P. Then
![]() $S(v) \subset {\tilde R}$
is a basis of V and that consists of pairwise alternating twisted roots.
$S(v) \subset {\tilde R}$
is a basis of V and that consists of pairwise alternating twisted roots.
Proof. That
![]() $S(v)$
is a basis follows from the assumption that P is generic and simple. Suppose
$S(v)$
is a basis follows from the assumption that P is generic and simple. Suppose
![]() ${\tilde {\beta }}, {\tilde {\beta }}' \in S(v)$
are not alternating. Then
${\tilde {\beta }}, {\tilde {\beta }}' \in S(v)$
are not alternating. Then
![]() $(\beta ,\beta ' ) < 0$
so there is a root of the form
$(\beta ,\beta ' ) < 0$
so there is a root of the form
![]() $\beta " = b \beta + c \beta '$
with
$\beta " = b \beta + c \beta '$
with
![]() $b,c \in \mathbb {R}_{>0}$
. Thus, there is a twisted root of the form
$b,c \in \mathbb {R}_{>0}$
. Thus, there is a twisted root of the form
![]() ${\tilde {\beta }}" = b{\tilde {\beta }} + c{\tilde {\beta }}'$
. Clearly,
${\tilde {\beta }}" = b{\tilde {\beta }} + c{\tilde {\beta }}'$
. Clearly,
![]() $a_{{\tilde {\beta }}"} = \max _{x \in P} (x,{\tilde {\beta }}") \leq b a_{{\tilde {\beta }}} + c a_{{\tilde {\beta }}'}$
. We have
$a_{{\tilde {\beta }}"} = \max _{x \in P} (x,{\tilde {\beta }}") \leq b a_{{\tilde {\beta }}} + c a_{{\tilde {\beta }}'}$
. We have
implying that
![]() $(v,{\tilde {\beta }}") \in a_{{\tilde {\beta }}"}$
and thus
$(v,{\tilde {\beta }}") \in a_{{\tilde {\beta }}"}$
and thus
![]() ${\tilde {\beta }}" \in S(v)$
, contradicting the statement that
${\tilde {\beta }}" \in S(v)$
, contradicting the statement that
![]() $S(v)$
is a basis.
$S(v)$
is a basis.
13.
 $(W,c)$
-polypositroids
$(W,c)$
-polypositroids
Definition 13.1. A convex polytope
![]() $P \subset V$
is called a
$P \subset V$
is called a
![]() $(W,c)$
-polypositroid if it is both a generalized W-permutohedron and a
$(W,c)$
-polypositroid if it is both a generalized W-permutohedron and a
![]() $(W,c)$
-twisted alcoved polytope. In other words, we require that
$(W,c)$
-twisted alcoved polytope. In other words, we require that
-
(1) every edge
 $[u,v]$
of P is parallel to a coroot
$[u,v]$
of P is parallel to a coroot
 $\alpha ^{\vee }\in R^{\vee }$
, i.e.,
$\alpha ^{\vee }\in R^{\vee }$
, i.e.,
 $u-v= a \alpha ^{\vee }$
,
$u-v= a \alpha ^{\vee }$
,
 $a\in \mathbb {R}_{>0}$
;
$a\in \mathbb {R}_{>0}$
; -
(2) every facet of P is orthogonal to a twisted root
 $(I-c)^{-1}(\beta )\in \tilde R$
,
$(I-c)^{-1}(\beta )\in \tilde R$
,
 $\beta \in R$
.
$\beta \in R$
.
By Example 12.3, Definition 13.1 agrees with the notion of “polypositroid in
![]() $H_0$
” of Definition 3.8 with the choices of Example 10.8. If W and c are understood to be fixed, we may simply use the name “polypositroid.” Let us hasten to point out that the notion of a
$H_0$
” of Definition 3.8 with the choices of Example 10.8. If W and c are understood to be fixed, we may simply use the name “polypositroid.” Let us hasten to point out that the notion of a
![]() $(W,c)$
-polypositroid does not depend on a choice of
$(W,c)$
-polypositroid does not depend on a choice of
![]() $R^+$
.
$R^+$
.
Remark 13.2. Suppose c and
![]() $c'$
are two Coxeter elements. Then there exists
$c'$
are two Coxeter elements. Then there exists
![]() $w \in W$
so that
$w \in W$
so that
![]() $c' = wcw^{-1}$
. We have that P is a
$c' = wcw^{-1}$
. We have that P is a
![]() $(W,c')$
-polypositroid if and only if
$(W,c')$
-polypositroid if and only if
![]() $w \cdot P$
is a
$w \cdot P$
is a
![]() $(W,c)$
-polypositroid.
$(W,c)$
-polypositroid.
Remark 13.3. The notion of
![]() $(W,c)$
-polypositroid is unchanged if the root and coroot vectors are dilated by scalars. In particular, the notion of
$(W,c)$
-polypositroid is unchanged if the root and coroot vectors are dilated by scalars. In particular, the notion of
![]() $(W,c)$
-polypositroid is identical for a root system R and its dual
$(W,c)$
-polypositroid is identical for a root system R and its dual
![]() $R^{\vee }$
.
$R^{\vee }$
.
14. Coxeter necklaces
Consider the cone
Since for
![]() $i = 1,2,\ldots ,r$
we have
$i = 1,2,\ldots ,r$
we have
![]() $\beta ^{\vee }_i \in R^+$
and
$\beta ^{\vee }_i \in R^+$
and
![]() $c^{-1}(\beta ^{\vee }_i) \in R^-$
, we have
$c^{-1}(\beta ^{\vee }_i) \in R^-$
, we have
![]() $A\subseteq C\cap (-c(C))$
. But, in general, these two cones are not equal to each other. Note also that A depends only on c and
$A\subseteq C\cap (-c(C))$
. But, in general, these two cones are not equal to each other. Note also that A depends only on c and
![]() $R^+$
, and not on the choice of reduced factorization of c (though the enumeration of the set
$R^+$
, and not on the choice of reduced factorization of c (though the enumeration of the set
![]() $\{\beta ^{\vee }_1,\beta ^{\vee }_2,\ldots ,\beta ^{\vee }_r\}$
does depend on the reduced factorization).
$\{\beta ^{\vee }_1,\beta ^{\vee }_2,\ldots ,\beta ^{\vee }_r\}$
does depend on the reduced factorization).
Definition 14.1. A
![]() $(W,R^+,c)$
-Coxeter necklace is a sequence
$(W,R^+,c)$
-Coxeter necklace is a sequence
![]() $(v_0,v_1,\ldots ,v_{h-1})$
of points in V, such that for any
$(v_0,v_1,\ldots ,v_{h-1})$
of points in V, such that for any
![]() $i=1,\dots ,h$
,
$i=1,\dots ,h$
,
Here, we set
![]() $v_{i+h} := v_i$
and thus,
$v_{i+h} := v_i$
and thus,
![]() $v_h:=v_0$
.
$v_h:=v_0$
.
With the choices made in Example 10.8, Definition 14.1 agrees with the notion of Coxeter necklace in Definition 6.1.
Proposition 14.2. Suppose that
![]() $\mathbf {v} = (v_0,v_1,\ldots ,v_{h-1})$
is a
$\mathbf {v} = (v_0,v_1,\ldots ,v_{h-1})$
is a
![]() $(W,R^+,c)$
-Coxeter necklace. Then each point
$(W,R^+,c)$
-Coxeter necklace. Then each point
![]() $v_i$
is a vertex of the
$v_i$
is a vertex of the
![]() $(W,c)$
-twisted alcoved polytope
$(W,c)$
-twisted alcoved polytope
 $$ \begin{align*}Q(\mathbf{v}) := \bigcap_{i=0}^{h-1}( v_i + c^i(C)). \end{align*} $$
$$ \begin{align*}Q(\mathbf{v}) := \bigcap_{i=0}^{h-1}( v_i + c^i(C)). \end{align*} $$
In particular,
![]() $\mathrm {env}_c(\mathbf {v}) = Q(\mathbf {v})$
.
$\mathrm {env}_c(\mathbf {v}) = Q(\mathbf {v})$
.
Proof. It suffices to show that
![]() $v_i \in Q(\mathbf {v})$
, or equivalently,
$v_i \in Q(\mathbf {v})$
, or equivalently,
![]() $v_j-v_i\in c^i(C)$
, for any
$v_j-v_i\in c^i(C)$
, for any
![]() $i,j\in \{0,\dots ,h-1\}$
. Rotating by a power of c, it is enough to show that
$i,j\in \{0,\dots ,h-1\}$
. Rotating by a power of c, it is enough to show that
![]() $v_j - v_0\in C$
. Equivalently, we need to show that
$v_j - v_0\in C$
. Equivalently, we need to show that
![]() $(v_j-v_0,\omega _k)\geq 0$
, for any j and any k.
$(v_j-v_0,\omega _k)\geq 0$
, for any j and any k.
We have
![]() $v_j - v_0 = (v_1- v_0) + (v_2 - v_1) + \cdots + (v_j-v_{j-1})$
. The vector
$v_j - v_0 = (v_1- v_0) + (v_2 - v_1) + \cdots + (v_j-v_{j-1})$
. The vector
![]() $v_{m+1}-v_m$
is a nonnegative linear combination of the coroots
$v_{m+1}-v_m$
is a nonnegative linear combination of the coroots
![]() $c^m\, \beta ^{\vee }_i$
, for
$c^m\, \beta ^{\vee }_i$
, for
![]() $i=1,\dots ,r$
. According to Lemma 10.6, if
$i=1,\dots ,r$
. According to Lemma 10.6, if
![]() $j\leq M(k^{\star })$
, then
$j\leq M(k^{\star })$
, then
![]() $(\beta ^{\vee },\omega _k)\geq 0$
, for all coroots
$(\beta ^{\vee },\omega _k)\geq 0$
, for all coroots
![]() $\beta ^{\vee }$
involved in the expression of
$\beta ^{\vee }$
involved in the expression of
![]() $v_{m+1}-v_m$
, for
$v_{m+1}-v_m$
, for
![]() $m=j-1,j-2,\dots ,0$
. This implies that
$m=j-1,j-2,\dots ,0$
. This implies that
![]() $(v_j-v_0,\omega _k)\geq 0$
.
$(v_j-v_0,\omega _k)\geq 0$
.
On the other hand, if
![]() $j \geq M(k^{\star })$
, we can express
$j \geq M(k^{\star })$
, we can express
![]() $v_j-v_0$
in a different way as
$v_j-v_0$
in a different way as
![]() $v_j-v_0= v_j-v_h=-((v_{j+1}-v_{j})+(v_{j+2}-v_{j+1})+\cdots +(v_{h}-v_{h-1}))$
. Now, according to Lemma 10.6, we have
$v_j-v_0= v_j-v_h=-((v_{j+1}-v_{j})+(v_{j+2}-v_{j+1})+\cdots +(v_{h}-v_{h-1}))$
. Now, according to Lemma 10.6, we have
![]() $(\beta ^{\vee },\omega _k)\leq 0$
, for any coroot
$(\beta ^{\vee },\omega _k)\leq 0$
, for any coroot
![]() $\beta ^{\vee }$
involved in the expression of
$\beta ^{\vee }$
involved in the expression of
![]() $v_{m+1}-v_m$
, for
$v_{m+1}-v_m$
, for
![]() $m=j,j+1,\dots ,h-1$
. Thus, again, we get
$m=j,j+1,\dots ,h-1$
. Thus, again, we get
![]() $(v_j-v_0,\omega _k)\geq 0$
.
$(v_j-v_0,\omega _k)\geq 0$
.
Lemma 14.3. Let
![]() $R_1^+$
and
$R_1^+$
and
![]() $R_2^+$
be two choices of positive roots for R compatible with c. Then there is a bijection
$R_2^+$
be two choices of positive roots for R compatible with c. Then there is a bijection
![]() $\mathbf {v} \mapsto \mathbf {v}'$
between
$\mathbf {v} \mapsto \mathbf {v}'$
between
![]() $(W,R_1^+,c)$
-Coxeter necklaces and
$(W,R_1^+,c)$
-Coxeter necklaces and
![]() $(W,R_2^+,c)$
-Coxeter necklaces, such that
$(W,R_2^+,c)$
-Coxeter necklaces, such that
![]() $Q(\mathbf {v}) = Q(\mathbf {v}')$
.
$Q(\mathbf {v}) = Q(\mathbf {v}')$
.
Proof. By Proposition 10.4, we may assume that
![]() $R_2^+ = s_1 \cdot R_1^+$
, and
$R_2^+ = s_1 \cdot R_1^+$
, and
![]() $c = s_1 s_2 \cdots s_r$
is a reduced factorization in
$c = s_1 s_2 \cdots s_r$
is a reduced factorization in
![]() $R_1^+$
. Letting
$R_1^+$
. Letting
![]() $s^{\prime }_i = s_1 s_i s_1$
be the simple generators of
$s^{\prime }_i = s_1 s_i s_1$
be the simple generators of
![]() $R_2^+$
, we have
$R_2^+$
, we have
![]() $c =s^{\prime }_2 \cdots s^{\prime }_r s^{\prime }_1$
. Let
$c =s^{\prime }_2 \cdots s^{\prime }_r s^{\prime }_1$
. Let
![]() $\beta _1,\beta _2,\ldots $
be the enumeration of R associated to the factorization
$\beta _1,\beta _2,\ldots $
be the enumeration of R associated to the factorization
![]() $c = s_1 s_2 \cdots s_r$
. Then the enumeration of R associated to
$c = s_1 s_2 \cdots s_r$
. Then the enumeration of R associated to
![]() $c =s^{\prime }_2 \cdots s^{\prime }_r s^{\prime }_1$
is
$c =s^{\prime }_2 \cdots s^{\prime }_r s^{\prime }_1$
is
![]() $\beta _2, \beta _3,\ldots $
.
$\beta _2, \beta _3,\ldots $
.
Let
![]() $v^{\prime }_i = v_i + [\beta ^{\vee }_{ir+1}](v_{i+1}-v_i)$
, where
$v^{\prime }_i = v_i + [\beta ^{\vee }_{ir+1}](v_{i+1}-v_i)$
, where
![]() $[\beta ^{\vee }_{ir+1}](v_{i+1}-v_i)$
denotes the coefficient of
$[\beta ^{\vee }_{ir+1}](v_{i+1}-v_i)$
denotes the coefficient of
![]() $\beta ^{\vee }_{ir+1}$
in the vector
$\beta ^{\vee }_{ir+1}$
in the vector
![]() $v_{i+1}-v_i$
which lies in the cone
$v_{i+1}-v_i$
which lies in the cone
![]() $c^i(A)$
spanned by
$c^i(A)$
spanned by
![]() $\beta ^{\vee }_{ir+1},\beta ^{\vee }_{ir+2},\ldots ,\beta ^{\vee }_{(i+1)r}$
. It is clear that
$\beta ^{\vee }_{ir+1},\beta ^{\vee }_{ir+2},\ldots ,\beta ^{\vee }_{(i+1)r}$
. It is clear that
![]() $\mathbf {v} \mapsto \mathbf {v}'$
is a bijection from
$\mathbf {v} \mapsto \mathbf {v}'$
is a bijection from
![]() $(W,R_1^+,c)$
-Coxeter necklaces to
$(W,R_1^+,c)$
-Coxeter necklaces to
![]() $(W,R_2^+,c)$
-Coxeter necklaces. We claim that
$(W,R_2^+,c)$
-Coxeter necklaces. We claim that
![]() $Q(\mathbf {v}) = Q(\mathbf {v}')$
. It suffices to show that each
$Q(\mathbf {v}) = Q(\mathbf {v}')$
. It suffices to show that each
![]() $v^{\prime }_j$
belongs to
$v^{\prime }_j$
belongs to
![]() $Q(\mathbf {v})$
, and we can reduce to showing that
$Q(\mathbf {v})$
, and we can reduce to showing that
![]() $v^{\prime }_j - v_0 = (v_j - v_0) + a \beta ^{\vee }_{jr+1} \in A$
, where
$v^{\prime }_j - v_0 = (v_j - v_0) + a \beta ^{\vee }_{jr+1} \in A$
, where
![]() $a \in \mathbb {R}_{\geq 0}$
. The proof is identical to that of Proposition 14.2, using Lemma 10.6.
$a \in \mathbb {R}_{\geq 0}$
. The proof is identical to that of Proposition 14.2, using Lemma 10.6.
Lemma 14.4. Let c and
![]() $c' = wcw^{-1}$
be two Coxeter elements. Then
$c' = wcw^{-1}$
be two Coxeter elements. Then
![]() $\mathbf {v}$
is a
$\mathbf {v}$
is a
![]() $(W,R^+,c)$
-Coxeter necklace if and only if
$(W,R^+,c)$
-Coxeter necklace if and only if
![]() $w \cdot \mathbf {v}$
is a
$w \cdot \mathbf {v}$
is a
![]() $(W,w \cdot R^+, c')$
-Coxeter necklace. We have
$(W,w \cdot R^+, c')$
-Coxeter necklace. We have
![]() $w \cdot Q(\mathbf {v}) = Q(w \cdot \mathbf {v})$
, where
$w \cdot Q(\mathbf {v}) = Q(w \cdot \mathbf {v})$
, where
![]() $Q(\mathbf {v})$
denotes a
$Q(\mathbf {v})$
denotes a
![]() $(W,c)$
-twisted alcoved polytope and
$(W,c)$
-twisted alcoved polytope and
![]() $Q(w\cdot v)$
denotes a
$Q(w\cdot v)$
denotes a
![]() $(W,c')$
-twisted alcoved polytope.
$(W,c')$
-twisted alcoved polytope.
Proof. Clear from the definitions.
We call a Coxeter necklace
![]() $\mathbf {v} = (v_0,v_1,\ldots ,v_{h-1})$
generic if each difference
$\mathbf {v} = (v_0,v_1,\ldots ,v_{h-1})$
generic if each difference
![]() $v_{i}-v_{i-1}$
belongs to the interior of the cone
$v_{i}-v_{i-1}$
belongs to the interior of the cone
![]() $c^i(A)$
.
$c^i(A)$
.
Lemma 14.5. Suppose that
![]() $\mathbf {v}$
is a generic
$\mathbf {v}$
is a generic
![]() $(W,R^+,c)$
-Coxeter necklace. Then for each twisted root
$(W,R^+,c)$
-Coxeter necklace. Then for each twisted root
![]() $\omega $
, the face
$\omega $
, the face
![]() $\{ x \in Q(\mathbf {v}) \mid (x,\omega ) =0 \}$
contains at most one of the vertices
$\{ x \in Q(\mathbf {v}) \mid (x,\omega ) =0 \}$
contains at most one of the vertices
![]() $v_0,v_1,\ldots ,v_{h-1}$
. In particular,
$v_0,v_1,\ldots ,v_{h-1}$
. In particular,
![]() $Q(\mathbf {v})$
is a generic
$Q(\mathbf {v})$
is a generic
![]() $(W,c)$
-twisted alcoved polytope.
$(W,c)$
-twisted alcoved polytope.
Proof. By acting with c, we may assume that
![]() $\omega = \omega _k$
, where
$\omega = \omega _k$
, where
![]() $k \in \{1,2,\ldots ,r\}$
. In the proof of Proposition 14.2, we note that we have the strict inequalities
$k \in \{1,2,\ldots ,r\}$
. In the proof of Proposition 14.2, we note that we have the strict inequalities
![]() $(\beta ^{\vee }_k,\omega _k)>0$
and
$(\beta ^{\vee }_k,\omega _k)>0$
and
![]() $(\beta ^{\vee }_{k-r},\omega _k) < 0$
.
$(\beta ^{\vee }_{k-r},\omega _k) < 0$
.
Whereas Theorem 11.2 describes a generalized W-permutohedron as an intersection of
![]() $|W|$
cones, our next result describes a
$|W|$
cones, our next result describes a
![]() $(W,c)$
-polypositroid as an intersection of h cones.
$(W,c)$
-polypositroid as an intersection of h cones.
Proposition 14.6. Fix a Coxeter element c. Suppose P is a W-generalized permutohedron. Then for any choice of
![]() $R^+$
, we have
$R^+$
, we have
 $$ \begin{align*}\mathrm{env}_c(P) = Q(\mathbf{v}) = \bigcap_{i=0}^{h-1} (v_i + c^i(C)), \end{align*} $$
$$ \begin{align*}\mathrm{env}_c(P) = Q(\mathbf{v}) = \bigcap_{i=0}^{h-1} (v_i + c^i(C)), \end{align*} $$
where
![]() $\mathbf {v} = (v_0,\dots ,v_{h-1})$
is a
$\mathbf {v} = (v_0,\dots ,v_{h-1})$
is a
![]() $(W,R^+,c)$
-Coxeter necklace. In particular, this holds for P a
$(W,R^+,c)$
-Coxeter necklace. In particular, this holds for P a
![]() $(W,c)$
-polypositroid, in which case,
$(W,c)$
-polypositroid, in which case,
![]() $\mathrm {env}_c(P) = P$
.
$\mathrm {env}_c(P) = P$
.
Proof. By Proposition 12.6, any
![]() $(W,c)$
-twisted alcoved polytope has the form
$(W,c)$
-twisted alcoved polytope has the form
![]() $P = \bigcap _{i=0}^{h-1} (v_i + c^i(C))$
for some uniquely determined points
$P = \bigcap _{i=0}^{h-1} (v_i + c^i(C))$
for some uniquely determined points
![]() $v_i$
, and thus this holds for
$v_i$
, and thus this holds for
![]() $\mathrm {env}_c(P)$
.
$\mathrm {env}_c(P)$
.
Since P is also a W-generalized permutohedron, by Corollary 11.3, we must have
![]() $v_i = v_{c^i}$
, the vertex of P that is the minimum in
$v_i = v_{c^i}$
, the vertex of P that is the minimum in
![]() $c^i(C)$
-dominance order. Let us show that the conditions
$c^i(C)$
-dominance order. Let us show that the conditions
![]() $v_i-v_{i-1} \in c^i(A)$
hold. It is enough to show this for
$v_i-v_{i-1} \in c^i(A)$
hold. It is enough to show this for
![]() $i=0$
(the general case is obtained by the action of
$i=0$
(the general case is obtained by the action of
![]() $c^i$
). Consider the following sequence of vertices that connect
$c^i$
). Consider the following sequence of vertices that connect
![]() $v_0=v_{id}$
with
$v_0=v_{id}$
with
![]() $v_1=v_{c}$
:
$v_1=v_{c}$
:
According to Theorem 11.4,
![]() $v_{s_1 s_2\cdots s_i}-v_{s_1 s_2 \cdots s_{i-1}} = a_i \, s_1\cdots s_{i-1}(\alpha ^{\vee }_i)$
, for
$v_{s_1 s_2\cdots s_i}-v_{s_1 s_2 \cdots s_{i-1}} = a_i \, s_1\cdots s_{i-1}(\alpha ^{\vee }_i)$
, for
![]() $a_i\in \mathbb {R}_{\geq 0}$
. Thus,
$a_i\in \mathbb {R}_{\geq 0}$
. Thus,
![]() $v_1 - v_0 = \sum _{i=1}^r a_i\, \beta ^{\vee }_i \in A$
. We conclude that
$v_1 - v_0 = \sum _{i=1}^r a_i\, \beta ^{\vee }_i \in A$
. We conclude that
![]() $\mathbf {v}=(v_0,v_1,\ldots ,v_{h-1})$
is a Coxeter necklace, as required.
$\mathbf {v}=(v_0,v_1,\ldots ,v_{h-1})$
is a Coxeter necklace, as required.
15. Balanced arrays
Definition 15.1. A W-balanced array is a collection
![]() $(m_{\alpha })_{\alpha \in R}$
of nonnegative real numbers satisfying the equality
$(m_{\alpha })_{\alpha \in R}$
of nonnegative real numbers satisfying the equality
A W-balanced pair is a pair
![]() $((m_{\alpha }),z)$
consisting of a W-balanced array
$((m_{\alpha }),z)$
consisting of a W-balanced array
![]() $(m_{\alpha })$
and a vector
$(m_{\alpha })$
and a vector
![]() $z \in V$
.
$z \in V$
.
Now let
![]() $c=s_1s_2\cdots s_r$
be a standard Coxeter element with respect to
$c=s_1s_2\cdots s_r$
be a standard Coxeter element with respect to
![]() $R^+$
and
$R^+$
and
![]() $\beta _1,\beta _2,\ldots ,$
be the corresponding ordering of roots. We define a Coxeter necklace
$\beta _1,\beta _2,\ldots ,$
be the corresponding ordering of roots. We define a Coxeter necklace
by setting
![]() $v_0 = z$
and
$v_0 = z$
and
 $$ \begin{align} v_i = v_{i-1} + \sum_{k=(i-1)r+1}^{ir} m_{\beta_k} \beta^{\vee}_k \end{align} $$
$$ \begin{align} v_i = v_{i-1} + \sum_{k=(i-1)r+1}^{ir} m_{\beta_k} \beta^{\vee}_k \end{align} $$
for
![]() $i=1,2,\ldots ,h-1$
. The equality
$i=1,2,\ldots ,h-1$
. The equality
![]() $v_h = v_0$
follows from (15.1) and Proposition 10.3.
$v_h = v_0$
follows from (15.1) and Proposition 10.3.
Proposition 15.2. The map
![]() $((m_{\alpha }),z) \mapsto \mathbf {v}((m_{\alpha }),z)$
is a bijection between W-balanced pairs and
$((m_{\alpha }),z) \mapsto \mathbf {v}((m_{\alpha }),z)$
is a bijection between W-balanced pairs and
![]() $(W,R^+,c)$
-Coxeter necklaces, for any choice of
$(W,R^+,c)$
-Coxeter necklaces, for any choice of
![]() $(R^+,c)$
.
$(R^+,c)$
.
Proof. In (15.2), the
![]() $m_{\beta }$
can be recovered from
$m_{\beta }$
can be recovered from
![]() $\mathbf {v}((m_{\alpha }),z)$
because
$\mathbf {v}((m_{\alpha }),z)$
because
![]() $\{\beta ^{\vee }_{(i-1)r+1}, \ldots ,\beta ^{\vee }_{ir}\}$
is a basis. The result easily follows.
$\{\beta ^{\vee }_{(i-1)r+1}, \ldots ,\beta ^{\vee }_{ir}\}$
is a basis. The result easily follows.
Proposition 15.3. Fix a W-balanced pair
![]() $((m_{\alpha }),z)$
. Then the
$((m_{\alpha }),z)$
. Then the
![]() $(W,R^+,c)$
-Coxeter necklace
$(W,R^+,c)$
-Coxeter necklace
![]() $\mathbf {v}((m_{\alpha }),z)$
depends on
$\mathbf {v}((m_{\alpha }),z)$
depends on
![]() $(R^+,c)$
and not on the reduced word of c.
$(R^+,c)$
and not on the reduced word of c.
Proof. Changing the reduced word of c replaces
![]() $\{\beta _1,\ldots ,\beta _r\}$
by a permutation of the same set.
$\{\beta _1,\ldots ,\beta _r\}$
by a permutation of the same set.
For a balanced pair
![]() $((m_{\alpha }),z)$
, we also define a Coxeter belt
$((m_{\alpha }),z)$
, we also define a Coxeter belt
by setting
![]() $u_0 = z$
and
$u_0 = z$
and
for
![]() $i = 1,2,\ldots ,hr-1$
. Note that given
$i = 1,2,\ldots ,hr-1$
. Note that given
![]() $((m_{\alpha }),z)$
, the Coxeter belt depends on
$((m_{\alpha }),z)$
, the Coxeter belt depends on
![]() $R^+$
, on c, and on a reduced word for c.
$R^+$
, on c, and on a reduced word for c.
Suppose
![]() $R^+$
has simple roots
$R^+$
has simple roots
![]() $\alpha _1,\ldots ,\alpha _r$
. Then
$\alpha _1,\ldots ,\alpha _r$
. Then
![]() $s_1 R^+$
is also a positive system, and its simple roots are
$s_1 R^+$
is also a positive system, and its simple roots are
![]() $-\alpha _1, s_1 \alpha _2,\ldots , s_1 \alpha _r$
.
$-\alpha _1, s_1 \alpha _2,\ldots , s_1 \alpha _r$
.
Proposition 15.4. The
![]() $(W,R^+,c)$
-Coxeter belt for the W-balanced pair
$(W,R^+,c)$
-Coxeter belt for the W-balanced pair
![]() $((m_{\alpha }),z)$
with respect to
$((m_{\alpha }),z)$
with respect to
![]() $(R^+,c=s_1s_2\cdots s_r)$
is the same, up to a cyclic shift, as the
$(R^+,c=s_1s_2\cdots s_r)$
is the same, up to a cyclic shift, as the
![]() $(W,s_1R^+,c)$
-Coxeter belt for the balanced pair
$(W,s_1R^+,c)$
-Coxeter belt for the balanced pair
![]() $((m_{\alpha }),z'=u_1)$
with respect to
$((m_{\alpha }),z'=u_1)$
with respect to
![]() $(s_1 R^+,c = (s_1s_2s_1) \cdots (s_1s_r s_1) s_1)$
.
$(s_1 R^+,c = (s_1s_2s_1) \cdots (s_1s_r s_1) s_1)$
.
Proof. Follows from Proposition 10.4.
Given a balanced pair
![]() $((m_{\alpha }),z)$
, let
$((m_{\alpha }),z)$
, let
![]() $Q((m_{\alpha }),z):=Q(\mathbf {v}((m_{\alpha }),z))$
.
$Q((m_{\alpha }),z):=Q(\mathbf {v}((m_{\alpha }),z))$
.
Corollary 15.5. Let
![]() $((m_{\alpha }),z)$
be a balanced pair. Then
$((m_{\alpha }),z)$
be a balanced pair. Then
![]() $\mathrm {env}_c(\mathbf {u}((m_{\alpha }),z)) = Q((m_{\alpha }),z)$
, and each point of the Coxeter belt
$\mathrm {env}_c(\mathbf {u}((m_{\alpha }),z)) = Q((m_{\alpha }),z)$
, and each point of the Coxeter belt
![]() $\mathbf {u}((m_{\alpha }),z)$
is a vertex of
$\mathbf {u}((m_{\alpha }),z)$
is a vertex of
![]() $Q((m_{\alpha }),z)$
.
$Q((m_{\alpha }),z)$
.
Proof. By Proposition 14.2, we have
![]() $\mathrm {env}_c(\mathbf {v}((m_{\alpha }),z)) = Q((m_{\alpha }),z)$
. Since the Coxeter necklace
$\mathrm {env}_c(\mathbf {v}((m_{\alpha }),z)) = Q((m_{\alpha }),z)$
. Since the Coxeter necklace
![]() $\mathbf {v}((m_{\alpha }),z)$
is a subset of the Coxeter belt
$\mathbf {v}((m_{\alpha }),z)$
is a subset of the Coxeter belt
![]() $\mathbf {u}((m_{\alpha }),z)$
, we have
$\mathbf {u}((m_{\alpha }),z)$
, we have
![]() $\mathrm {env}_c(\mathbf {u}((m_{\alpha }),z)) \supseteq \mathrm {env}_c(\mathbf {v}((m_{\alpha }),z))$
. To establish equality, it suffices to show that each
$\mathrm {env}_c(\mathbf {u}((m_{\alpha }),z)) \supseteq \mathrm {env}_c(\mathbf {v}((m_{\alpha }),z))$
. To establish equality, it suffices to show that each
![]() $u_i$
belongs to
$u_i$
belongs to
![]() $Q((m_{\alpha }),z)$
. By combining the action of c with Proposition 15.4, it suffices to show that
$Q((m_{\alpha }),z)$
. By combining the action of c with Proposition 15.4, it suffices to show that
![]() $u_1 \in Q(\mathbf {v}((m_{\alpha }),z))$
. This follows from Lemma 14.3.
$u_1 \in Q(\mathbf {v}((m_{\alpha }),z))$
. This follows from Lemma 14.3.
The claim that every point on the Coxeter belt is a vertex of
![]() $Q((m_{\alpha }),z)$
follows from applying Proposition 14.2 to the
$Q((m_{\alpha }),z)$
follows from applying Proposition 14.2 to the
![]() $(W,s_1R^+,c)$
-Coxeter necklace appearing in Proposition 15.4.
$(W,s_1R^+,c)$
-Coxeter necklace appearing in Proposition 15.4.
Definition 15.6. A
![]() $(W,c)$
-balancedtope is a polytope of the form
$(W,c)$
-balancedtope is a polytope of the form
![]() $Q((m_{\alpha }),z)$
.
$Q((m_{\alpha }),z)$
.
By Propositions 15.3 and 15.4 and Corollary 15.5, up to changing z (or equivalently, up to a translation), the
![]() $(W,c)$
-balancedtope
$(W,c)$
-balancedtope
![]() $Q((m_{\alpha }),z)$
does not depend on the choice of reduced word of c, or on the choice of
$Q((m_{\alpha }),z)$
does not depend on the choice of reduced word of c, or on the choice of
![]() $R^+$
.
$R^+$
.
16. Prepolypositroids
Let
![]() $\mathbb {R}^{{\tilde R}} = \{(a_{\omega })_{\omega \in {\tilde R}}\}$
denote the vector space whose coordinates are labeled by the set
$\mathbb {R}^{{\tilde R}} = \{(a_{\omega })_{\omega \in {\tilde R}}\}$
denote the vector space whose coordinates are labeled by the set
![]() ${\tilde R}$
of twisted roots. Let
${\tilde R}$
of twisted roots. Let
![]() ${\mathcal {C}}_{\mathrm {pre}}^{W,c} \subset \mathbb {R}^{{\tilde R}}$
denote the cone cut out by the inequalities
${\mathcal {C}}_{\mathrm {pre}}^{W,c} \subset \mathbb {R}^{{\tilde R}}$
denote the cone cut out by the inequalities
for
![]() $k \in \mathbb {Z}$
and
$k \in \mathbb {Z}$
and
![]() $1 \leq m \leq r$
. Recall that
$1 \leq m \leq r$
. Recall that
![]() $j \to i$
if i and j are connected in the Dynkin diagram and i occurs before j in all reduced words of c. The twisted roots appearing in (16.1) all belong to the set
$j \to i$
if i and j are connected in the Dynkin diagram and i occurs before j in all reduced words of c. The twisted roots appearing in (16.1) all belong to the set
![]() $\{c^{m-1}\omega _k = {\tilde {\beta }}_{k+(m-1)r},{\tilde {\beta }}_{k+(m-1)r+1},\ldots ,{\tilde {\beta }}_{k+mr}= c^m \omega _k\}$
.
$\{c^{m-1}\omega _k = {\tilde {\beta }}_{k+(m-1)r},{\tilde {\beta }}_{k+(m-1)r+1},\ldots ,{\tilde {\beta }}_{k+mr}= c^m \omega _k\}$
.
Proposition 16.1. The inequalities (16.1) depend on c and not on the choice of reduced word of c, or on the choice of
![]() $R^+$
.
$R^+$
.
Proof. That the inequalities (16.1) do not depend on the reduced word of c is apparent. For the second part, using Proposition 10.4, we need to check what happens if we replace
![]() $R^+$
by
$R^+$
by
![]() $s_1 R^+$
, where
$s_1 R^+$
, where
![]() $c = s_1s_2 \cdots s_r$
. If
$c = s_1s_2 \cdots s_r$
. If
![]() $j \to _{c,R^+} i$
, then we also have
$j \to _{c,R^+} i$
, then we also have
![]() $j \to _{c,s_1R^+} i$
unless one of
$j \to _{c,s_1R^+} i$
unless one of
![]() $i,j$
is equal to 1, in which case, the relation reverses. This is exactly the required condition for the inequalities (16.1) to be preserved when
$i,j$
is equal to 1, in which case, the relation reverses. This is exactly the required condition for the inequalities (16.1) to be preserved when
![]() $R^+$
is changed to
$R^+$
is changed to
![]() $s_1 R^+$
.
$s_1 R^+$
.
Example 16.2. Let us take
![]() $(W,R^+,c)$
, as in Examples 10.8 and 12.3. In the notation of Part I, we have
$(W,R^+,c)$
, as in Examples 10.8 and 12.3. In the notation of Part I, we have
![]() $a_{ij} = a_{h_i - h_j}$
. The inequalities (16.1) are of three types: (1)
$a_{ij} = a_{h_i - h_j}$
. The inequalities (16.1) are of three types: (1)
![]() $a_{i, i+1} + a_{i+1,i+2} \geq a_{i,i+2}$
, (2)
$a_{i, i+1} + a_{i+1,i+2} \geq a_{i,i+2}$
, (2)
![]() $a_{i+1, i} + a_{i+2,i+1} \geq a_{i+2,i}$
, and (3)
$a_{i+1, i} + a_{i+2,i+1} \geq a_{i+2,i}$
, and (3)
![]() $a_{i,j} + a_{i+1,j+1} \geq a_{i,j+1} + a_{j,j+1}$
, where
$a_{i,j} + a_{i+1,j+1} \geq a_{i,j+1} + a_{j,j+1}$
, where
![]() $i,i+1,j,j+1$
are distinct. The inequalities (1) and (2) are special cases of the triangle inequality (4.2), while (3) is a special case of (4.3). It will follow from Theorem 17.3, and can be verified directly, that the inequalities (4.2) and (4.3) are consequences of the smaller set of inequalities (16.1). Indeed, the
$i,i+1,j,j+1$
are distinct. The inequalities (1) and (2) are special cases of the triangle inequality (4.2), while (3) is a special case of (4.3). It will follow from Theorem 17.3, and can be verified directly, that the inequalities (4.2) and (4.3) are consequences of the smaller set of inequalities (16.1). Indeed, the
![]() $n(n-1) = |R|$
inequalities in (16.1) are exactly the facet inequalities appearing in Corollary 6.13.
$n(n-1) = |R|$
inequalities in (16.1) are exactly the facet inequalities appearing in Corollary 6.13.
Example 16.3. Let us take
![]() $(W,R^+,c)$
as in Example 10.9. Using Proposition 10.5, we have
$(W,R^+,c)$
as in Example 10.9. Using Proposition 10.5, we have
![]() $\omega _1 = e_1, \omega _2= e_1+e_2,\ldots ,\omega _{r-1} = e_1+e_2+\cdots +e_{r-1}$
, and
$\omega _1 = e_1, \omega _2= e_1+e_2,\ldots ,\omega _{r-1} = e_1+e_2+\cdots +e_{r-1}$
, and
![]() $\omega _r = \frac {1}{2}(e_1+e_2+\cdots +e_r)$
. The inequalities (16.1) are:
$\omega _r = \frac {1}{2}(e_1+e_2+\cdots +e_r)$
. The inequalities (16.1) are:
 $$ \begin{align*} a_{c^{m-1}\omega_1}+ a_{c^m\omega_1} &\geq a_{c^{m-1} \omega_2} \\ a_{c^{m-1}\omega_i}+ a_{c^m\omega_i} &\geq a_{c^m \omega_{i-1}}+ a_{c^{m-1} \omega_{i+1}} &\mbox{for } i=2,\ldots,r-2\\ a_{c^{m-1}\omega_{r-1}}+ a_{c^m\omega_{r-1}} &\geq a_{c^m \omega_{r-2}}+ a_{c^{m-1} \omega_{r}} \\ a_{c^{m-1}\omega_{r}}+ a_{c^m\omega_{r}} &\geq 2a_{c^m \omega_{r-1}}. \end{align*} $$
$$ \begin{align*} a_{c^{m-1}\omega_1}+ a_{c^m\omega_1} &\geq a_{c^{m-1} \omega_2} \\ a_{c^{m-1}\omega_i}+ a_{c^m\omega_i} &\geq a_{c^m \omega_{i-1}}+ a_{c^{m-1} \omega_{i+1}} &\mbox{for } i=2,\ldots,r-2\\ a_{c^{m-1}\omega_{r-1}}+ a_{c^m\omega_{r-1}} &\geq a_{c^m \omega_{r-2}}+ a_{c^{m-1} \omega_{r}} \\ a_{c^{m-1}\omega_{r}}+ a_{c^m\omega_{r}} &\geq 2a_{c^m \omega_{r-1}}. \end{align*} $$
Definition 16.4. A
![]() $(W,c)$
-prepolypositroid is a
$(W,c)$
-prepolypositroid is a
![]() $(W,c)$
-twisted alcoved polytope cut out by the halfspaces
$(W,c)$
-twisted alcoved polytope cut out by the halfspaces
![]() $(x,\omega ) \leq a_{\omega }$
,
$(x,\omega ) \leq a_{\omega }$
,
![]() $\omega \in {\tilde R}$
, where
$\omega \in {\tilde R}$
, where
![]() $a_{\omega } \in {\mathcal {C}}_{\mathrm {pre}}^{W,c}$
.
$a_{\omega } \in {\mathcal {C}}_{\mathrm {pre}}^{W,c}$
.
We call
![]() ${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
the cone of
${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
the cone of
![]() $(W,c)$
-prepolypositroids.
$(W,c)$
-prepolypositroids.
Theorem 16.5. There are natural isomorphisms between the following three cones:
-
1. the cone of
 $(W,c)$
-prepolypositroids.
$(W,c)$
-prepolypositroids. -
2. the cone of W-balanced pairs
 $((m_{\alpha }), z)$
;
$((m_{\alpha }), z)$
; -
3. the cone of
 $(W,R^+,c)$
-Coxeter necklaces for any choice of
$(W,R^+,c)$
-Coxeter necklaces for any choice of
 $R^+$
.
$R^+$
.
Furthermore, if a
![]() $(W,c)$
-prepolypositroid P arises from
$(W,c)$
-prepolypositroid P arises from
![]() $(a_{\omega }) \in {\mathcal {C}}_{\mathrm {pre}}^{W,c}$
, then each
$(a_{\omega }) \in {\mathcal {C}}_{\mathrm {pre}}^{W,c}$
, then each
![]() $a_{\omega } \in \mathbb {R}$
is minimal, that is, is a value of the support function of P.
$a_{\omega } \in \mathbb {R}$
is minimal, that is, is a value of the support function of P.
Proposition 15.2 gives the isomorphism between (2) and (3). For the remainder of this section, our aim is to show that
![]() $((m_{\alpha }), z) \mapsto Q((m_{\alpha }), z)$
is a bijection between balanced pairs and
$((m_{\alpha }), z) \mapsto Q((m_{\alpha }), z)$
is a bijection between balanced pairs and
![]() $(W,c)$
-prepolypositroids.
$(W,c)$
-prepolypositroids.
Proposition 16.6. We have
for any k and any m.
Proof. By Proposition 16.1, to verify the claim, we can assume that
![]() $c = s_1s_2 \cdots s_r$
and verify the equality
$c = s_1s_2 \cdots s_r$
and verify the equality
where the sum is over all j connected to
![]() $1$
in the Dynkin diagram. The left hand side is equal to
$1$
in the Dynkin diagram. The left hand side is equal to
![]() $2\omega _1 - \alpha _1$
, and we check that
$2\omega _1 - \alpha _1$
, and we check that
 $$ \begin{align*}(\alpha_j^{\vee}, 2\omega_1 - \alpha_1) = \begin{cases} -A_{j1} & \mbox{if } j \mbox{ is connected to } i \mbox{ in the Dynkin diagram} \\ 0 & \mbox{otherwise.} \end{cases}\\[-34pt] \end{align*} $$
$$ \begin{align*}(\alpha_j^{\vee}, 2\omega_1 - \alpha_1) = \begin{cases} -A_{j1} & \mbox{if } j \mbox{ is connected to } i \mbox{ in the Dynkin diagram} \\ 0 & \mbox{otherwise.} \end{cases}\\[-34pt] \end{align*} $$
Given a
![]() $(W,c)$
-balancedtope
$(W,c)$
-balancedtope
![]() $Q((m_{\alpha }),z)$
, we define a collection
$Q((m_{\alpha }),z)$
, we define a collection
![]() $(a_{\omega })$
of real numbers, one for each twisted root
$(a_{\omega })$
of real numbers, one for each twisted root
![]() $\omega \in {\tilde R}$
by
$\omega \in {\tilde R}$
by
Proposition 16.7. For any
![]() $(W,c)$
-balancedtope
$(W,c)$
-balancedtope
![]() $Q((m_{\alpha }),z)$
, the collection
$Q((m_{\alpha }),z)$
, the collection
![]() $(a_{\omega })$
satisfies the inequalities (16.1).
$(a_{\omega })$
satisfies the inequalities (16.1).
Proof. It follows from Lemma 10.7 that the inequalities (16.1) are equivalent to the set of “negated” inequalities
for all k and m. By Proposition 16.1, to verify the claim, we can assume that
![]() $c = s_1s_2 \cdots s_r$
and verify just one of the inequalities (16.4), say
$c = s_1s_2 \cdots s_r$
and verify just one of the inequalities (16.4), say
where the sum is over all j connected to
![]() $1$
in the Dynkin diagram. By Proposition 16.6, the claim is translation invariant. Thus, we may assume that
$1$
in the Dynkin diagram. By Proposition 16.6, the claim is translation invariant. Thus, we may assume that
![]() $v_0 = 0$
, that is,
$v_0 = 0$
, that is,
![]() $z = 0$
.
$z = 0$
.
The maximum of
![]() $-\omega _1,\ldots ,-\omega _r$
on
$-\omega _1,\ldots ,-\omega _r$
on
![]() $Q((m_{\alpha }),z)$
occurs at the vertex
$Q((m_{\alpha }),z)$
occurs at the vertex
![]() $v_0$
. The maximum of
$v_0$
. The maximum of
![]() $-c\omega _1$
occurs at vertex
$-c\omega _1$
occurs at vertex
![]() $v_1$
, where the value taken is greater than or equal to
$v_1$
, where the value taken is greater than or equal to
![]() $(-c\omega _1, v_0) = 0$
. The required inequality now follows from
$(-c\omega _1, v_0) = 0$
. The required inequality now follows from
![]() $a_{-c\omega _1} \geq 0$
.
$a_{-c\omega _1} \geq 0$
.
By Proposition 16.7, we have an injective and linear map
![]() $((m_{\alpha }),z) \mapsto (a_{\omega })$
from the cone of W-balanced pairs to the cone
$((m_{\alpha }),z) \mapsto (a_{\omega })$
from the cone of W-balanced pairs to the cone
![]() ${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
of
${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
of
![]() $(W,c)$
-prepolypositroids. The cone of balanced pairs has exactly
$(W,c)$
-prepolypositroids. The cone of balanced pairs has exactly
![]() $|R|$
facets, given by
$|R|$
facets, given by
![]() $m_{\alpha } = 0$
, for
$m_{\alpha } = 0$
, for
![]() $\alpha \in R$
. Each equality
$\alpha \in R$
. Each equality
![]() $a_{-c^{m-1}\omega _k}+ a_{-c^m\omega _k} = \sum _{k \to i} -A_{ik} a_{-c^m \omega _i}+ \sum _{i \to k} -A_{ik} a_{-c^{m-1} \omega _i}$
defines a face of
$a_{-c^{m-1}\omega _k}+ a_{-c^m\omega _k} = \sum _{k \to i} -A_{ik} a_{-c^m \omega _i}+ \sum _{i \to k} -A_{ik} a_{-c^{m-1} \omega _i}$
defines a face of
![]() ${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
.
${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
.
Lemma 16.8. The map
![]() $((m_{\alpha }),z) \mapsto (a_{\omega })$
sends the facet
$((m_{\alpha }),z) \mapsto (a_{\omega })$
sends the facet
![]() $\{m_{\alpha } = 0\}$
of the cone of W-balanced pairs to the face
$\{m_{\alpha } = 0\}$
of the cone of W-balanced pairs to the face
![]() $\{a_{-c^{m-1}\omega _k}+ a_{-c^m\omega _k} = \sum _{k \to i} -A_{ik} a_{-c^m \omega _i}+ \sum _{i \to k} -A_{ik} a_{-c^{m-1} \omega _i}\}$
of
$\{a_{-c^{m-1}\omega _k}+ a_{-c^m\omega _k} = \sum _{k \to i} -A_{ik} a_{-c^m \omega _i}+ \sum _{i \to k} -A_{ik} a_{-c^{m-1} \omega _i}\}$
of
![]() ${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
, where
${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
, where
![]() $\alpha $
satisfies
$\alpha $
satisfies
![]() $\tilde {\alpha } = (I-c)^{-1} \alpha = c^{m-1} \omega _k$
.
$\tilde {\alpha } = (I-c)^{-1} \alpha = c^{m-1} \omega _k$
.
Proof. In the end of the proof of Proposition 16.7, it suffices to note that
![]() $a_{-c\omega _1} = m_{\alpha _1}$
. Indeed, for
$a_{-c\omega _1} = m_{\alpha _1}$
. Indeed, for
![]() $i \in [2,r]$
, we have
$i \in [2,r]$
, we have
but
![]() $(\beta ^{\vee }_1,c\omega _1) = (\alpha ^{\vee }_1,\omega _1-\alpha _1) = -1$
.
$(\beta ^{\vee }_1,c\omega _1) = (\alpha ^{\vee }_1,\omega _1-\alpha _1) = -1$
.
It follows that each equality
![]() $\{a_{-c^{m-1}\omega _k}+ a_{-c^m\omega _k} = \sum _{k \to i} -A_{ik} a_{-c^m \omega _i}+ \sum _{i \to k} -A_{ik} a_{-c^{m-1} \omega _i}\}$
defines a facet of
$\{a_{-c^{m-1}\omega _k}+ a_{-c^m\omega _k} = \sum _{k \to i} -A_{ik} a_{-c^m \omega _i}+ \sum _{i \to k} -A_{ik} a_{-c^{m-1} \omega _i}\}$
defines a facet of
![]() ${\mathcal {C}}_{\mathrm { pre}}^{W,c}$
.
${\mathcal {C}}_{\mathrm { pre}}^{W,c}$
.
Proof of Theorem 16.5
We compare (1) and (2). It follows from Lemma 16.8 that each equality
![]() $a_{-c^{m-1}\omega _k}+ a_{-c^m\omega _k} = \sum _{k \to i} -A_{ik} a_{-c^m \omega _i}+ \sum _{i \to k} -A_{ik} a_{-c^{m-1} \omega _i}$
defines a facet of the cone of
$a_{-c^{m-1}\omega _k}+ a_{-c^m\omega _k} = \sum _{k \to i} -A_{ik} a_{-c^m \omega _i}+ \sum _{i \to k} -A_{ik} a_{-c^{m-1} \omega _i}$
defines a facet of the cone of
![]() $(W,c)$
-prepolypositroids. It then follows from the same lemma that the map
$(W,c)$
-prepolypositroids. It then follows from the same lemma that the map
![]() $((m_{\alpha }),z) \mapsto (a_{\omega })$
is a linear isomorphism, completing the proof of the isomorphism between the three cones.
$((m_{\alpha }),z) \mapsto (a_{\omega })$
is a linear isomorphism, completing the proof of the isomorphism between the three cones.
17. From prepolypositroids to polypositroids
17.1. Alcoved envelope of generalized W-permutohedra
Theorem 17.1.
-
1. The cone of generalized W-permutohedra
 ${\mathcal {C}}_{\mathrm {sub}}^W$
projects to the cone of
${\mathcal {C}}_{\mathrm {sub}}^W$
projects to the cone of
 $(W,c)$
-prepolypositroids
$(W,c)$
-prepolypositroids
 ${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
by projecting the vector
${\mathcal {C}}_{\mathrm {pre}}^{W,c}$
by projecting the vector
 $(a_{w\omega _i}) \in \mathbb {R}^{W \cdot \{\omega _1,\ldots ,\omega _r\}}$
of (11.1) to
$(a_{w\omega _i}) \in \mathbb {R}^{W \cdot \{\omega _1,\ldots ,\omega _r\}}$
of (11.1) to
 $(a_{c^m \omega _i}) \in \mathbb {R}^{{\tilde R}}$
.
$(a_{c^m \omega _i}) \in \mathbb {R}^{{\tilde R}}$
. -
2. The
 $(W,c)$
-twisted alcoved envelope of a generalized W-permutohedron is a
$(W,c)$
-twisted alcoved envelope of a generalized W-permutohedron is a
 $(W,c)$
-prepolypositroid.
$(W,c)$
-prepolypositroid. -
3. The vertices
 $(v_{\mathrm {id}}, v_c, v_{c^2},\ldots , v_{c^{h-1}})$
of a generalized W-permutohedron are a
$(v_{\mathrm {id}}, v_c, v_{c^2},\ldots , v_{c^{h-1}})$
of a generalized W-permutohedron are a
 $(W,c)$
-Coxeter necklace.
$(W,c)$
-Coxeter necklace.
Proof. (3) was established in the proof of Proposition 14.6. (1) and (2) thus follow from Theorem 16.5.
Conjecture 17.2. The maps in Theorem 17.1(1) are surjective.
17.2. Type A
Theorem 17.3. Suppose R is of type A. Then every
![]() $(W,c)$
-prepolypositroid is also a generalized W-permutohedron. Thus, the class of
$(W,c)$
-prepolypositroid is also a generalized W-permutohedron. Thus, the class of
![]() $(W,c)$
-prepolypositroids is identical to the class of
$(W,c)$
-prepolypositroids is identical to the class of
![]() $(W,c)$
-polypositroids.
$(W,c)$
-polypositroids.
Proof. Let c be the Coxeter element of Example 10.8. Then by Theorems 16.5 and 6.12, the class of
![]() $(W,c)$
-prepolypositroids is exactly the class of polypositroids. Thus, the result holds in this case. Now, let
$(W,c)$
-prepolypositroids is exactly the class of polypositroids. Thus, the result holds in this case. Now, let
![]() $c' = wcw^{-1}$
be an arbitrary Coxeter element. Since the class of generalized W-permutohedra is preserved under the action of W, the result holds by Remark 13.2.
$c' = wcw^{-1}$
be an arbitrary Coxeter element. Since the class of generalized W-permutohedra is preserved under the action of W, the result holds by Remark 13.2.
It follows from Theorem 17.3 that Conjecture 17.2 holds in type A.
17.3. A prepolypositroid that is not a polypositroid
We give an example of a
![]() $(W,c)$
-prepolypositroid that is not a
$(W,c)$
-prepolypositroid that is not a
![]() $(W,c)$
-polypositroid. Let
$(W,c)$
-polypositroid. Let
![]() $R = D_4$
. We take as positive simple roots
$R = D_4$
. We take as positive simple roots
and let
![]() $c = s_1s_2s_3s_4$
, so that the Dynkin diagram is oriented
$c = s_1s_2s_3s_4$
, so that the Dynkin diagram is oriented

The ordering of the 24 roots of R is given by (here,
![]() $r=4$
and
$r=4$
and
![]() $h=6$
)
$h=6$
)
 $$ \begin{align*} &(1, -1, 0, 0), &&(1, 0, -1, 0), &&(1, 0, 0, -1), &&(1, 0, 0, 1), \\ &(0, 1, -1,0), &&(1, 1, 0, 0), &&(0, 1, 0, 1), &&(0, 1, 0, -1), \\ &(1, 0, 1, 0), &&(0, 1,1, 0), &&(0, 0, 1, -1), &&(0, 0, 1, 1), \\ &(-1, 1, 0, 0), &&(-1, 0, 1, 0), &&(-1, 0, 0, 1), &&(-1, 0, 0, -1), \\ &(0, -1, 1, 0), &&(-1, -1, 0, 0), &&(0, -1, 0, -1), &&(0, -1, 0, 1), \\ &(-1, 0, -1, 0), &&(0, -1, -1, 0), &&(0, 0, -1, 1), &&(0, 0, -1, -1), \end{align*} $$
$$ \begin{align*} &(1, -1, 0, 0), &&(1, 0, -1, 0), &&(1, 0, 0, -1), &&(1, 0, 0, 1), \\ &(0, 1, -1,0), &&(1, 1, 0, 0), &&(0, 1, 0, 1), &&(0, 1, 0, -1), \\ &(1, 0, 1, 0), &&(0, 1,1, 0), &&(0, 0, 1, -1), &&(0, 0, 1, 1), \\ &(-1, 1, 0, 0), &&(-1, 0, 1, 0), &&(-1, 0, 0, 1), &&(-1, 0, 0, -1), \\ &(0, -1, 1, 0), &&(-1, -1, 0, 0), &&(0, -1, 0, -1), &&(0, -1, 0, 1), \\ &(-1, 0, -1, 0), &&(0, -1, -1, 0), &&(0, 0, -1, 1), &&(0, 0, -1, -1), \end{align*} $$
and we see that
![]() $M(k) = 3$
for
$M(k) = 3$
for
![]() $k=1,2,3,4$
. The twisted roots
$k=1,2,3,4$
. The twisted roots
![]() ${\tilde R}$
are, in the same order,
${\tilde R}$
are, in the same order,
 $$ \begin{align*} &(1, 0, 0, 0), &&(1, 1, 0, 0), &&(\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}), &&(\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2},\tfrac{1}{2}), \\ &(0, 1, 0, 0), &&(0, 1, 1, 0), &&(-\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}), &&(-\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}), \\ &(0, 0, 1, 0), &&(-1, 0, 1, 0), &&(-\tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}), &&(-\tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}),\\ &(-1, 0, 0, 0), &&(-1, -1, 0, 0), &&(-\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}), &&(-\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}), \\ &(0, -1, 0, 0), &&(0, -1, -1, 0), &&(\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}), &&(\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}), \\ &(0, 0, -1, 0), &&(1, 0, -1, 0), &&(\tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}), &&(\tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}). \end{align*} $$
$$ \begin{align*} &(1, 0, 0, 0), &&(1, 1, 0, 0), &&(\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}), &&(\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2},\tfrac{1}{2}), \\ &(0, 1, 0, 0), &&(0, 1, 1, 0), &&(-\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}), &&(-\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}), \\ &(0, 0, 1, 0), &&(-1, 0, 1, 0), &&(-\tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}), &&(-\tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}, \tfrac{1}{2}),\\ &(-1, 0, 0, 0), &&(-1, -1, 0, 0), &&(-\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}), &&(-\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}), \\ &(0, -1, 0, 0), &&(0, -1, -1, 0), &&(\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}), &&(\tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}), \\ &(0, 0, -1, 0), &&(1, 0, -1, 0), &&(\tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}, \tfrac{1}{2}), &&(\tfrac{1}{2}, \tfrac{1}{2}, -\tfrac{1}{2}, -\tfrac{1}{2}). \end{align*} $$
We consider the Coxeter necklace
The polytope
![]() $Q(\mathbf {v})$
is a
$Q(\mathbf {v})$
is a
![]() $(W,c)$
-prepolypositroid, and the
$(W,c)$
-prepolypositroid, and the
![]() $a_{\omega }$
are given by
$a_{\omega }$
are given by
in the same order as
![]() ${\tilde R}$
. The inequalities (16.1) can be verified directly. For example, we have
${\tilde R}$
. The inequalities (16.1) can be verified directly. For example, we have
Now, one computes (for example, by [Reference Gawrilow and JoswigGJ]) that
![]() $Q(\mathbf {v})$
has seven vertices
$Q(\mathbf {v})$
has seven vertices
and that there is an edge connecting
![]() $(1,0,1,2)$
and
$(1,0,1,2)$
and
![]() $(1,0,1,0)$
. Indeed, one can check that this edge is the intersection of the three facets indexed by
$(1,0,1,0)$
. Indeed, one can check that this edge is the intersection of the three facets indexed by
![]() $(1,0,0,0)$
,
$(1,0,0,0)$
,
![]() $(0,0,1,0)$
, and
$(0,0,1,0)$
, and
![]() $(0,-1,0,0)$
. This edge is in the direction
$(0,-1,0,0)$
. This edge is in the direction
![]() $(0,0,0,1)$
, which is not a root direction. Thus,
$(0,0,0,1)$
, which is not a root direction. Thus,
![]() $Q(\mathbf {v})$
is not a generalized W-permutohedron.
$Q(\mathbf {v})$
is not a generalized W-permutohedron.
It turns out that
![]() $Q(\mathbf {v})$
is the
$Q(\mathbf {v})$
is the
![]() $(W,c)$
-twisted alcoved envelope of a generalized permutohedron, namely, one with vertices
$(W,c)$
-twisted alcoved envelope of a generalized permutohedron, namely, one with vertices
consistent with Conjecture 17.2.
18. Prepolypositroids and finite type cluster algebras
We briefly recall some basic facts concerning finite type cluster algebras, following [Reference Yang and ZelevinskyYZ]. Let
![]() ${\mathcal {A}}(W,R^+,c)$
denote the finite type cluster algebra with principal coefficients of type R and associated to a compatible pair
${\mathcal {A}}(W,R^+,c)$
denote the finite type cluster algebra with principal coefficients of type R and associated to a compatible pair
![]() $(R^+,c)$
. Usually, the choice of positive system
$(R^+,c)$
. Usually, the choice of positive system
![]() $R^+$
is not made explicit in the theory of cluster algebras, but for our purposes, it is necessary.
$R^+$
is not made explicit in the theory of cluster algebras, but for our purposes, it is necessary.
The cluster algebra
![]() ${\mathcal {A}}(W,R^+,c)$
is a commutative subring of the field of rational functions
${\mathcal {A}}(W,R^+,c)$
is a commutative subring of the field of rational functions
![]() $\mathbb {C}(x_1,x_2,\ldots ,x_r,y_1,y_2,\ldots ,y_r)$
, where
$\mathbb {C}(x_1,x_2,\ldots ,x_r,y_1,y_2,\ldots ,y_r)$
, where
![]() $x_i$
(respectively,
$x_i$
(respectively,
![]() $y_i$
) are called initial mutable cluster variables (respectively, coefficient variables). The choice of c determines an initial exchange matrix B, given by the formula [Reference Yang and ZelevinskyYZ, (1.4)]. The cluster algebra
$y_i$
) are called initial mutable cluster variables (respectively, coefficient variables). The choice of c determines an initial exchange matrix B, given by the formula [Reference Yang and ZelevinskyYZ, (1.4)]. The cluster algebra
![]() ${\mathcal {A}}(W,R^+,c)$
contains a distinguished set of cluster variables, and associated to each cluster variable is a g-vector which belongs to V.
${\mathcal {A}}(W,R^+,c)$
contains a distinguished set of cluster variables, and associated to each cluster variable is a g-vector which belongs to V.
Theorem 18.1 [Reference Yang and ZelevinskyYZ, Theorems 1.4 and 1.10]
The cluster variablesFootnote 2
![]() $x_{{\tilde {\beta }}}$
of
$x_{{\tilde {\beta }}}$
of
![]() ${\mathcal {A}}(W,R^+,c)$
are labeled by the set
${\mathcal {A}}(W,R^+,c)$
are labeled by the set
where
![]() $M(i)$
is defined in Proposition 10.3. Furthermore,
$M(i)$
is defined in Proposition 10.3. Furthermore,
![]() ${\tilde {\beta }}$
is the g-vector of
${\tilde {\beta }}$
is the g-vector of
![]() $x_{{\tilde {\beta }}}$
.
$x_{{\tilde {\beta }}}$
.
It follows from Lemma 10.7 that
![]() $\pm \omega _i \in \Pi (c)$
. The cluster variables
$\pm \omega _i \in \Pi (c)$
. The cluster variables
![]() $x_{{\tilde {\beta }}}$
are arranged into clusters. We say that
$x_{{\tilde {\beta }}}$
are arranged into clusters. We say that
![]() ${\tilde {\beta }}$
and
${\tilde {\beta }}$
and
![]() ${\tilde {\gamma }}$
(or
${\tilde {\gamma }}$
(or
![]() $x_{{\tilde {\beta }}}$
and
$x_{{\tilde {\beta }}}$
and
![]() $x_{{\tilde {\gamma }}}$
) are
$x_{{\tilde {\gamma }}}$
) are
![]() $(R^+,c)$
-compatible, or simply compatible, if they belong to the same cluster; the clusters are exactly the collections of r pairwise-compatible cluster variables. The
$(R^+,c)$
-compatible, or simply compatible, if they belong to the same cluster; the clusters are exactly the collections of r pairwise-compatible cluster variables. The
![]() $(W,R^+,c)$
-cluster fan (also called the c-Cambrian fan) is the complete fan in V with cones
$(W,R^+,c)$
-cluster fan (also called the c-Cambrian fan) is the complete fan in V with cones
![]() $\mathrm {span}_{\geq 0}({\tilde {\gamma }}_1,{\tilde {\gamma }}_2,\ldots ,{\tilde {\gamma }}_s)$
, where
$\mathrm {span}_{\geq 0}({\tilde {\gamma }}_1,{\tilde {\gamma }}_2,\ldots ,{\tilde {\gamma }}_s)$
, where
![]() $\{{\tilde {\gamma }}_1,{\tilde {\gamma }}_2,\ldots ,{\tilde {\gamma }}_s\} \subset \Pi (c)$
is a set of pairwise
$\{{\tilde {\gamma }}_1,{\tilde {\gamma }}_2,\ldots ,{\tilde {\gamma }}_s\} \subset \Pi (c)$
is a set of pairwise
![]() $(R^+,c)$
-compatible vectors. A polytope with normal fan equal to the
$(R^+,c)$
-compatible vectors. A polytope with normal fan equal to the
![]() $(W,R^+,c)$
-cluster fan is called a
$(W,R^+,c)$
-cluster fan is called a
![]() $(W,R^+,c)$
-generalized associahedron. The following result combines work of Hohlweg et al. [Reference Hohlweg, Lange and ThomasHLT], Reading and Speyer [Reference Reading and SpeyerRS], and Yang and Zelevinsky [Reference Yang and ZelevinskyYZ, Remark 6.1].
$(W,R^+,c)$
-generalized associahedron. The following result combines work of Hohlweg et al. [Reference Hohlweg, Lange and ThomasHLT], Reading and Speyer [Reference Reading and SpeyerRS], and Yang and Zelevinsky [Reference Yang and ZelevinskyYZ, Remark 6.1].
Theorem 18.2. The
![]() $(W,R^+,c)$
-cluster fan is a refinement of the W-Coxeter fan. Furthermore,
$(W,R^+,c)$
-cluster fan is a refinement of the W-Coxeter fan. Furthermore,
![]() $(W,R^+,c)$
-generalized associahedra exist and are generalized W-permutohedra.
$(W,R^+,c)$
-generalized associahedra exist and are generalized W-permutohedra.
The W-Coxeter fan has maximal cones
![]() $C_w$
labeled by Weyl group elements
$C_w$
labeled by Weyl group elements
![]() $w \in W$
. By Theorem 18.2, every maximal cone of the
$w \in W$
. By Theorem 18.2, every maximal cone of the
![]() $(W,R^+,c)$
-cluster fan is a union of the cones
$(W,R^+,c)$
-cluster fan is a union of the cones
![]() $C_w$
. A
$C_w$
. A
![]() $(W,R^+,c)$
-singleton [Reference Hohlweg, Lange and ThomasHLT] is a Weyl group element w, such that
$(W,R^+,c)$
-singleton [Reference Hohlweg, Lange and ThomasHLT] is a Weyl group element w, such that
![]() $C_w$
is itself a maximal cone of the
$C_w$
is itself a maximal cone of the
![]() $(W,R^+,c)$
-cluster fan. Hohlweg et al. [Reference Hohlweg, Lange and ThomasHLT, Theorem 1.2] characterize the set of
$(W,R^+,c)$
-cluster fan. Hohlweg et al. [Reference Hohlweg, Lange and ThomasHLT, Theorem 1.2] characterize the set of
![]() $(W,R^+,c)$
-singletons as prefixes (up to commutation relations) of a particular reduced word of
$(W,R^+,c)$
-singletons as prefixes (up to commutation relations) of a particular reduced word of
![]() $w_0$
that depends on
$w_0$
that depends on
![]() $R^+$
and c.
$R^+$
and c.
The following result should be compared with Corollary 8.23.
Proposition 18.3. Let P be a generic simple
![]() $(W,c)$
-polypositroid. For any choice of
$(W,c)$
-polypositroid. For any choice of
![]() $R^+$
, and any
$R^+$
, and any
![]() $(W,R^+,c)$
-singleton w, the cone
$(W,R^+,c)$
-singleton w, the cone
![]() $C_w$
is a maximal cone of the normal fan
$C_w$
is a maximal cone of the normal fan
![]() ${\mathcal {N}}(P)$
.
${\mathcal {N}}(P)$
.
Proof. By definition, the normal fan
![]() ${\mathcal {N}}(P)$
is a coarsening of the W-Coxeter fan. It follows that there exists a maximal cone C of
${\mathcal {N}}(P)$
is a coarsening of the W-Coxeter fan. It follows that there exists a maximal cone C of
![]() ${\mathcal {N}}(P)$
that contains the simplicial cone
${\mathcal {N}}(P)$
that contains the simplicial cone
![]() $C_w$
. But each generating ray of
$C_w$
. But each generating ray of
![]() $C_w$
must be a generating ray of C, for otherwise, P would not be generic. But then we must have
$C_w$
must be a generating ray of C, for otherwise, P would not be generic. But then we must have
![]() $C = C_w$
, since both are simplicial cones.
$C = C_w$
, since both are simplicial cones.
The cluster variables are related by exchange relations. A distinguished subset of the exchange relations are called primitive exchange relations in [Reference Yang and ZelevinskyYZ].
Theorem 18.4 [Reference Yang and ZelevinskyYZ, Theorem 1.5]
The primitive exchange relations of
![]() ${\mathcal {A}}(W,R^+,c)$
are of the form
${\mathcal {A}}(W,R^+,c)$
are of the form
for
![]() $k = 1,2,\ldots ,r$
and
$k = 1,2,\ldots ,r$
and
for
![]() $k = 1,2,\ldots ,r$
and
$k = 1,2,\ldots ,r$
and
![]() $1 \leq m \leq M(k)$
, where Y is some monomial in the
$1 \leq m \leq M(k)$
, where Y is some monomial in the
![]() $y_i$
.
$y_i$
.
The relations (18.1) and (18.2) are homogeneous with respect to the g-vector grading. In particular, we have for each
![]() $k =1,2,\ldots ,r$
,
$k =1,2,\ldots ,r$
,
and for each
![]() $ 1 \leq m \leq M(k)$
,
$ 1 \leq m \leq M(k)$
,
The latter we recognize as a special case of Proposition 16.7.
More generally, we say that
![]() ${\tilde {\beta }}, {\tilde {\gamma }} \in \Gamma (c)$
are an exchangeable pair if we have a (necessarily unique) exchange relation that exchanges
${\tilde {\beta }}, {\tilde {\gamma }} \in \Gamma (c)$
are an exchangeable pair if we have a (necessarily unique) exchange relation that exchanges
![]() $x_{{\tilde {\beta }}}$
for
$x_{{\tilde {\beta }}}$
for
![]() $x_{{\tilde {\gamma }}}$
. This exchange relation takes the form
$x_{{\tilde {\gamma }}}$
. This exchange relation takes the form
 $$ \begin{align} x_{{\tilde{\beta}}} x_{{\tilde{\gamma}}} = \prod_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} x_{\tilde{\delta}}^{c_{\beta,\gamma;\delta}} + \text{ other monomial}, \end{align} $$
$$ \begin{align} x_{{\tilde{\beta}}} x_{{\tilde{\gamma}}} = \prod_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} x_{\tilde{\delta}}^{c_{\beta,\gamma;\delta}} + \text{ other monomial}, \end{align} $$
where
![]() $c_{\beta ,\gamma ;\delta }> 0$
, and
$c_{\beta ,\gamma ;\delta }> 0$
, and
![]() $E(\beta ,\gamma ) \subset \Pi (c)$
consists of elements that are pairwise compatible, and compatible with both
$E(\beta ,\gamma ) \subset \Pi (c)$
consists of elements that are pairwise compatible, and compatible with both
![]() ${\tilde {\beta }}$
and
${\tilde {\beta }}$
and
![]() ${\tilde {\gamma }}$
. Here, the key point is that one of the two monomials on the RHS of the exchange relation (18.5) does not involve any of the coefficient variables, known as sign-coherence. For a description of all the exchange relations in a principal coefficient finite-type cluster algebra, see [Reference Stella and TumarkinST]. Note that in type A, any incompatible pair
${\tilde {\gamma }}$
. Here, the key point is that one of the two monomials on the RHS of the exchange relation (18.5) does not involve any of the coefficient variables, known as sign-coherence. For a description of all the exchange relations in a principal coefficient finite-type cluster algebra, see [Reference Stella and TumarkinST]. Note that in type A, any incompatible pair
![]() $({\tilde {\beta }},{\tilde {\gamma }})$
is automatically exchangeable, but this is not the case in general type.
$({\tilde {\beta }},{\tilde {\gamma }})$
is automatically exchangeable, but this is not the case in general type.
The following is the main result of this section.
Theorem 18.5. Let P be a
![]() $(W,c)$
-prepolypositroid defined by the inequalities
$(W,c)$
-prepolypositroid defined by the inequalities
![]() $(x,\omega ) \leq a_{\omega }$
, where
$(x,\omega ) \leq a_{\omega }$
, where
![]() $(a_{\omega }) \in {\mathcal {C}}_{\mathrm {pre}}^{W,c}$
. Then for any choice of
$(a_{\omega }) \in {\mathcal {C}}_{\mathrm {pre}}^{W,c}$
. Then for any choice of
![]() $R^+$
compatible with c, and any pair
$R^+$
compatible with c, and any pair
![]() $(x_{{\tilde {\beta }}},x_{{\tilde {\gamma }}})$
of exchangeable cluster variables, we have
$(x_{{\tilde {\beta }}},x_{{\tilde {\gamma }}})$
of exchangeable cluster variables, we have
 $$ \begin{align} a_{{\tilde{\beta}}} + a_{{\tilde{\gamma}}} \geq \sum_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} c_{\beta,\gamma;\delta} a_{{\tilde{\delta}}} ,\end{align} $$
$$ \begin{align} a_{{\tilde{\beta}}} + a_{{\tilde{\gamma}}} \geq \sum_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} c_{\beta,\gamma;\delta} a_{{\tilde{\delta}}} ,\end{align} $$
where
![]() $E({\tilde {\beta }},{\tilde {\gamma }})$
and
$E({\tilde {\beta }},{\tilde {\gamma }})$
and
![]() $c_{\beta ,\gamma ;\delta }$
are defined in (18.5).
$c_{\beta ,\gamma ;\delta }$
are defined in (18.5).
Proof. We begin by noting that (18.5) is homogeneous with respect to the g-vector grading, so
 $$ \begin{align} {\tilde{\beta}} + {\tilde{\gamma}} = \sum_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} c_{\beta,\gamma;\delta} {\tilde{\delta}} \end{align} $$
$$ \begin{align} {\tilde{\beta}} + {\tilde{\gamma}} = \sum_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} c_{\beta,\gamma;\delta} {\tilde{\delta}} \end{align} $$
(see [Reference Stella and TumarkinST, Reference Padrol, Palu, Pilaud and PlamondonP4]). In [Reference Padrol, Palu, Pilaud and PlamondonP4, Proposition 2.22], it is shown that any linear dependence (18.7) is a positive sum of linear dependencies of the form (18.4). Replacing a linear dependence (18.4) by the corresponding inequality (16.1), we deduce that the inequality (18.6) is a positive sum of the inequalities (16.1).
Example 18.6. Pick
![]() $(W,R^+,c)$
as in Example 10.8. Then the inequalities (18.7) are all of the form (4.2) or (4.3).
$(W,R^+,c)$
as in Example 10.8. Then the inequalities (18.7) are all of the form (4.2) or (4.3).
The following is a variant of the noncrossing condition of Lemma 8.2.
Corollary 18.7. Let P be a generic simple
![]() $(W,c)$
-prepolypositroid and F be a face of P. Let
$(W,c)$
-prepolypositroid and F be a face of P. Let
![]() $S(F) \subset {\tilde R}$
be as defined in Section 12.2. Then for any choice of
$S(F) \subset {\tilde R}$
be as defined in Section 12.2. Then for any choice of
![]() $R^+$
compatible with c, and any exchangeable pair
$R^+$
compatible with c, and any exchangeable pair
![]() $({\tilde {\beta }},\gamma ) \in \Gamma (c)$
, we have that
$({\tilde {\beta }},\gamma ) \in \Gamma (c)$
, we have that
![]() $S(F)$
can contain at most one of
$S(F)$
can contain at most one of
![]() ${\tilde {\beta }}$
and
${\tilde {\beta }}$
and
![]() ${\tilde {\gamma }}$
.
${\tilde {\gamma }}$
.
Proof. Suppose we have an exchangeable pair
![]() ${\tilde {\beta }},{\tilde {\gamma }} \in S(F)$
. Let
${\tilde {\beta }},{\tilde {\gamma }} \in S(F)$
. Let
![]() $x \in F$
. Then, by (18.7), we have
$x \in F$
. Then, by (18.7), we have
 $$ \begin{align*}a_{{\tilde{\beta}}} + a_{{\tilde{\gamma}}} =(x,{\tilde{\beta}} + {\tilde{\gamma}}) = (x, \sum_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} c_{\beta,\gamma;\delta} {\tilde{\delta}}) \leq \sum_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} c_{\beta,\gamma;\delta} a_{{\tilde{\delta}}}. \end{align*} $$
$$ \begin{align*}a_{{\tilde{\beta}}} + a_{{\tilde{\gamma}}} =(x,{\tilde{\beta}} + {\tilde{\gamma}}) = (x, \sum_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} c_{\beta,\gamma;\delta} {\tilde{\delta}}) \leq \sum_{{\tilde{\delta}} \in E({\tilde{\beta}},{\tilde{\gamma}})} c_{\beta,\gamma;\delta} a_{{\tilde{\delta}}}. \end{align*} $$
By (18.6), we must have equality, giving
![]() ${\tilde {\delta }} \in S(F)$
for
${\tilde {\delta }} \in S(F)$
for
![]() ${\tilde {\delta }} \in E({\tilde {\beta }},{\tilde {\gamma }})$
. But then
${\tilde {\delta }} \in E({\tilde {\beta }},{\tilde {\gamma }})$
. But then
![]() $S(F)$
contains twisted roots that are not linearly independent, contradicting the assumption that P is generic simple.
$S(F)$
contains twisted roots that are not linearly independent, contradicting the assumption that P is generic simple.
Corollary 18.7 has the following defect: while
![]() $(W,c)$
-prepolypositroids depend only on the choice of c, the notion of an exchangeable pair
$(W,c)$
-prepolypositroids depend only on the choice of c, the notion of an exchangeable pair
![]() $({\tilde {\beta }},{\tilde {\gamma }})$
depends additionally on a choice of
$({\tilde {\beta }},{\tilde {\gamma }})$
depends additionally on a choice of
![]() $R^+$
. We thus pose the following question:
$R^+$
. We thus pose the following question:
Question 18.8. Which pairs of c-twisted roots are exchangeable for some choice of
![]() $R^+$
compatible with c?
$R^+$
compatible with c?
Corollary 18.9. Let P be a generic simple
![]() $(W,c)$
-prepolypositroid, and
$(W,c)$
-prepolypositroid, and
![]() $R^+$
be a positive system compatible with c. Then removing the facets
$R^+$
be a positive system compatible with c. Then removing the facets
![]() $(x,\omega ) \leq a_{\omega }$
indexed by facet normals
$(x,\omega ) \leq a_{\omega }$
indexed by facet normals
![]() $\omega \notin \Pi (c)$
gives a
$\omega \notin \Pi (c)$
gives a
![]() $(W,R^+,c)$
-generalized associahedron.
$(W,R^+,c)$
-generalized associahedron.
Proof. Removing the stated facets gives the polytope cut out by the inequalities
![]() $(x,\omega ) \leq a_{\omega }$
for
$(x,\omega ) \leq a_{\omega }$
for
![]() $\omega \in \Pi (c)$
. These
$\omega \in \Pi (c)$
. These
![]() $a_{\omega }$
satisfy
$a_{\omega }$
satisfy
for each
![]() $ 1 \leq m \leq M(k)$
. According to [Reference Padrol, Palu, Pilaud and PlamondonP4, Theorem 2.23], these inequalities cut out the deformation cone of the
$ 1 \leq m \leq M(k)$
. According to [Reference Padrol, Palu, Pilaud and PlamondonP4, Theorem 2.23], these inequalities cut out the deformation cone of the
![]() $(W,R^+,c)$
-generalized associahedron. In other words, the inequalities
$(W,R^+,c)$
-generalized associahedron. In other words, the inequalities
![]() $(x,\omega ) \leq a_{\omega }$
,
$(x,\omega ) \leq a_{\omega }$
,
![]() $\omega \in \Pi (c)$
define a
$\omega \in \Pi (c)$
define a
![]() $(W,R^+,c)$
-generalized associahedron.
$(W,R^+,c)$
-generalized associahedron.
On the other hand, not every maximal cone in the normal fan of a generic simple
![]() $(W,c)$
-prepolypositroid P is a maximal cone in some
$(W,c)$
-prepolypositroid P is a maximal cone in some
![]() $(W,R^+,c)$
-cluster fan, as the following example shows.
$(W,R^+,c)$
-cluster fan, as the following example shows.
Example 18.10. We continue the example from Section 17.3. By slightly perturbing the W-balanced pair associated to
![]() $\mathbf {v}$
, we obtain a generic simple
$\mathbf {v}$
, we obtain a generic simple
![]() $(W,c)$
-prepolypositroid
$(W,c)$
-prepolypositroid
![]() $Q(\mathbf {v}')$
whose normal fan is a refinement of that of
$Q(\mathbf {v}')$
whose normal fan is a refinement of that of
![]() $Q(\mathbf {v})$
but not a refinement of the W-Coxeter fan. There is a vertex v of
$Q(\mathbf {v})$
but not a refinement of the W-Coxeter fan. There is a vertex v of
![]() $Q(\mathbf {v}')$
with
$Q(\mathbf {v}')$
with
![]() $S(v)$
given by
$S(v)$
given by
The roots in
![]() $S(v)$
are pairwise c-noncrossing in the sense of Section 19.1. The dual cone is spanned by the vectors
$S(v)$
are pairwise c-noncrossing in the sense of Section 19.1. The dual cone is spanned by the vectors
the last of which is not in a direction of a root. Since the
![]() $(W,R^+,c)$
-cluster fan is a refinement of the W-Coxeter fan (Theorem 18.2), the vertex cone
$(W,R^+,c)$
-cluster fan is a refinement of the W-Coxeter fan (Theorem 18.2), the vertex cone
![]() $C_v$
in the normal fan of P is not a maximal cone for any cluster fan associated to
$C_v$
in the normal fan of P is not a maximal cone for any cluster fan associated to
![]() $(W,c)$
.
$(W,c)$
.
19. Normal fans of
 $(W,c)$
-prepolypositroids
$(W,c)$
-prepolypositroids
19.1. Coxeter noncrossing roots
Recall that a pair of distinct roots
![]() $(\beta ,\gamma ) \in R$
is said to be alternating if
$(\beta ,\gamma ) \in R$
is said to be alternating if
![]() $(\beta ,\gamma ) = (\gamma ,\beta )\geq 0$
. Let us say that
$(\beta ,\gamma ) = (\gamma ,\beta )\geq 0$
. Let us say that
![]() $(\beta ,\gamma ) \in R$
are c-noncrossing if either
$(\beta ,\gamma ) \in R$
are c-noncrossing if either
![]() $( \gamma ^{\vee },{\tilde {\beta }}) = 0$
or
$( \gamma ^{\vee },{\tilde {\beta }}) = 0$
or
![]() $(\beta ^{\vee },{\tilde {\gamma }}) = 0$
. We say that
$(\beta ^{\vee },{\tilde {\gamma }}) = 0$
. We say that
![]() $({\tilde {\beta }},{\tilde {\gamma }}) \in {\tilde R}$
are alternating (respectively, c-noncrossing) if
$({\tilde {\beta }},{\tilde {\gamma }}) \in {\tilde R}$
are alternating (respectively, c-noncrossing) if
![]() $(\beta ,\gamma ) \in R$
are. It is straightforward to see that with the choices in Example 10.8, “alternating” and “c-noncrossing” agrees with the corresponding notions in Part I.
$(\beta ,\gamma ) \in R$
are. It is straightforward to see that with the choices in Example 10.8, “alternating” and “c-noncrossing” agrees with the corresponding notions in Part I.
Lemma 19.1. Two roots
![]() $\beta ,\gamma $
are alternating (respectively, c-noncrossing) if and only if
$\beta ,\gamma $
are alternating (respectively, c-noncrossing) if and only if
![]() $c\beta ,c\gamma $
are alternating (respectively, c-noncrossing).
$c\beta ,c\gamma $
are alternating (respectively, c-noncrossing).
Lemma 19.2. Let c be a Coxeter element and
![]() $c' = wcw^{-1}$
. Then
$c' = wcw^{-1}$
. Then
![]() $(\beta ,\beta ')$
are c-noncrossing if and only if
$(\beta ,\beta ')$
are c-noncrossing if and only if
![]() $(w\beta ,w\beta ')$
are
$(w\beta ,w\beta ')$
are
![]() $c'$
-noncrossing.
$c'$
-noncrossing.
Conjecture 19.3. Let P be a generic simple
![]() $(W,c)$
-prepolypositroid, and suppose that
$(W,c)$
-prepolypositroid, and suppose that
![]() $({\tilde {\beta }},{\tilde {\gamma }}) \in {\tilde R}$
span a
$({\tilde {\beta }},{\tilde {\gamma }}) \in {\tilde R}$
span a
![]() $2$
-dimensional face of the normal fan of P. Then
$2$
-dimensional face of the normal fan of P. Then
![]() $(\beta ,\gamma )$
must be alternating and c-noncrossing.
$(\beta ,\gamma )$
must be alternating and c-noncrossing.
By Lemma 12.7, the alternating part of Conjecture 19.3 holds. By Lemma 8.2, Conjecture 19.3 holds when R is of type A. We will show in Proposition 19.12 that the condition “alternating and c-noncrossing” is essentially the same as cluster compatibility. Thus, Conjecture 19.3 is consistent with Corollary 18.7, since exchangeable pairs of cluster variables are incompatible (and the converse holds in type A).
Remark 19.4. The notion of c-noncrossing depends only on the choice of c, and not of
![]() $R^+$
. Furthermore,
$R^+$
. Furthermore,
![]() $(\beta ,\gamma )$
is c-noncrossing if and only if
$(\beta ,\gamma )$
is c-noncrossing if and only if
![]() $(-\beta ,\gamma )$
,
$(-\beta ,\gamma )$
,
![]() $(\beta ,-\gamma )$
, and
$(\beta ,-\gamma )$
, and
![]() $(-\beta ,-\gamma )$
are. This is consistent with our usage of “noncrossing” in type A for directed edges: two directed edges are noncrossing if the underlying undirected edges are.
$(-\beta ,-\gamma )$
are. This is consistent with our usage of “noncrossing” in type A for directed edges: two directed edges are noncrossing if the underlying undirected edges are.
19.2. Reflection factorizations
For
![]() $w \in W$
, write
$w \in W$
, write
![]() $\ell _R(w)$
for the length of the shortest factorization of w into reflections
$\ell _R(w)$
for the length of the shortest factorization of w into reflections
![]() $s_{\gamma } \in W$
,
$s_{\gamma } \in W$
,
![]() $\gamma \in R$
. We define a partial order
$\gamma \in R$
. We define a partial order
![]() $\leq _R$
on W by
$\leq _R$
on W by
Note that
![]() $\ell _R$
and
$\ell _R$
and
![]() $\leq _R$
do not depend on the choice of
$\leq _R$
do not depend on the choice of
![]() $R^+$
. It is wellknown that for any Coxeter element c, we have
$R^+$
. It is wellknown that for any Coxeter element c, we have
![]() $\ell _R(c) = r$
. We refer the reader to [Reference BessisBes, Reference Brady and WattBW] for general background on reflection factorizations and reflection order.
$\ell _R(c) = r$
. We refer the reader to [Reference BessisBes, Reference Brady and WattBW] for general background on reflection factorizations and reflection order.
19.3. Bipartite positive systems
We say that
![]() $(R^+,c)$
is bipartite, or c (respectively,
$(R^+,c)$
is bipartite, or c (respectively,
![]() $R^+$
) is bipartite with respect to
$R^+$
) is bipartite with respect to
![]() $R^+$
(respectively, c), if
$R^+$
(respectively, c), if
![]() $R^+$
is compatible with c, and, in addition,
$R^+$
is compatible with c, and, in addition,
where the partition
![]() $I = \{1,2,\ldots ,r\} = I_+ \sqcup I_-$
, with
$I = \{1,2,\ldots ,r\} = I_+ \sqcup I_-$
, with
![]() $I_+:= \{i_1, \ldots , i_t\}$
and
$I_+:= \{i_1, \ldots , i_t\}$
and
![]() $I_-:= \{i_{t+1},\ldots ,i_r\}$
makes the Dynkin diagram bipartite.
$I_-:= \{i_{t+1},\ldots ,i_r\}$
makes the Dynkin diagram bipartite.
Lemma 19.5. Let c be a fixed Coxeter element. Then a choice of
![]() $R^+$
bipartite with respect to c exists. There are exactly
$R^+$
bipartite with respect to c exists. There are exactly
![]() $2h$
bipartite
$2h$
bipartite
![]() $(R')^+$
with respect to c, and they are of the form
$(R')^+$
with respect to c, and they are of the form
![]() $\tau _+ \tau _- \tau _+ \cdots \tau _- \tau _+ R^+$
or
$\tau _+ \tau _- \tau _+ \cdots \tau _- \tau _+ R^+$
or
![]() $\tau _- \tau _+ \cdots \tau _- \tau _+ R^+$
.
$\tau _- \tau _+ \cdots \tau _- \tau _+ R^+$
.
Proof. There are exactly two orientations of the Dynkin diagram that correspond to bipartite
![]() $(R^+,c)$
. The claim thus follows from [Reference Kirillov and ThindKiTh, Theorem 3.6]. This theorem is stated for simply-laced root systems, but the statement and proof are valid also for multiply-laced Weyl groups.
$(R^+,c)$
. The claim thus follows from [Reference Kirillov and ThindKiTh, Theorem 3.6]. This theorem is stated for simply-laced root systems, but the statement and proof are valid also for multiply-laced Weyl groups.
When
![]() $(R^+,c)$
is bipartite, the ordering of Proposition 10.3 induces an ordering of R of the form
$(R^+,c)$
is bipartite, the ordering of Proposition 10.3 induces an ordering of R of the form
![]() $(A_1 \prec A_2 \prec \cdots \prec A_{2h}=A_0)$
, where
$(A_1 \prec A_2 \prec \cdots \prec A_{2h}=A_0)$
, where
![]() $|A_i| = t$
or
$|A_i| = t$
or
![]() $|A_i|=r-t$
depending on whether i is odd or i is even. The ordering within each
$|A_i|=r-t$
depending on whether i is odd or i is even. The ordering within each
![]() $A_i$
depends on the choice of a reduced word of c, but the sets
$A_i$
depends on the choice of a reduced word of c, but the sets
![]() $A_i$
themselves do not. We have
$A_i$
themselves do not. We have
 $$ \begin{align*}R^+ = \bigsqcup_{i=1}^h A_i \qquad R^- = \bigsqcup_{i=h+1}^{2h} A_i \qquad R_{\geq -1} = \bigsqcup_{i=0}^{h+1}A_i. \end{align*} $$
$$ \begin{align*}R^+ = \bigsqcup_{i=1}^h A_i \qquad R^- = \bigsqcup_{i=h+1}^{2h} A_i \qquad R_{\geq -1} = \bigsqcup_{i=0}^{h+1}A_i. \end{align*} $$
By Lemma 19.5, the ordering of R corresponding to another bipartite
![]() $(R')^+$
is of the form
$(R')^+$
is of the form
![]() $(A_k \prec A_{k+1} \prec A_{k+2} \prec \cdots \prec A_{k-1})$
.
$(A_k \prec A_{k+1} \prec A_{k+2} \prec \cdots \prec A_{k-1})$
.
We say that
![]() $\beta ,\gamma \in R$
are c-opposed if
$\beta ,\gamma \in R$
are c-opposed if
![]() $\beta \in A_i$
and
$\beta \in A_i$
and
![]() $\gamma \in A_{i+h}$
for some choice of bipartite
$\gamma \in A_{i+h}$
for some choice of bipartite
![]() $R^+$
with respect to c. The notion of c-opposed does not depend on the choice of bipartite
$R^+$
with respect to c. The notion of c-opposed does not depend on the choice of bipartite
![]() $R^+$
.
$R^+$
.
If
![]() $R^+$
and c are fixed, we write
$R^+$
and c are fixed, we write
![]() $\alpha \prec _{R^+,c} \alpha '$
(or simply
$\alpha \prec _{R^+,c} \alpha '$
(or simply
![]() $\alpha \prec \alpha '$
) if
$\alpha \prec \alpha '$
) if
![]() $\alpha $
precedes
$\alpha $
precedes
![]() $\alpha '$
in the ordering of R from Proposition 10.3.
$\alpha '$
in the ordering of R from Proposition 10.3.
Lemma 19.6 [Reference Brady and WattBW, Lemma 3.9]
Suppose that
![]() $\beta \prec _{R^+,c} \gamma $
are distinct positive roots. Then the following are equivalent:
$\beta \prec _{R^+,c} \gamma $
are distinct positive roots. Then the following are equivalent:
-
1.
 $s_{\beta } s_{\gamma } \leq _R c^{-1}$
;
$s_{\beta } s_{\gamma } \leq _R c^{-1}$
; -
2.
 $(\beta ^{\vee }, {\tilde {\gamma }}) = 0$
.
$(\beta ^{\vee }, {\tilde {\gamma }}) = 0$
.
Lemma 19.7 [Reference Brady and WattBW, Lemma 5.6]
Suppose that
![]() $\beta \prec _{R^+,c} \gamma $
are distinct positive roots. Then:
$\beta \prec _{R^+,c} \gamma $
are distinct positive roots. Then:
-
1. if
 $s_{\beta } s_{\gamma } \leq _R c^{-1}$
, we have
$s_{\beta } s_{\gamma } \leq _R c^{-1}$
, we have
 $(\beta ,\gamma ) \geq 0$
;
$(\beta ,\gamma ) \geq 0$
; -
2. if
 $s_{\gamma } s_{\beta } \leq _R c^{-1}$
, we have
$s_{\gamma } s_{\beta } \leq _R c^{-1}$
, we have
 $(\beta ,\gamma ) \leq 0$
.
$(\beta ,\gamma ) \leq 0$
.
Lemma 19.8. Suppose that
![]() $\beta ,\gamma \in R$
are c-opposed and
$\beta ,\gamma \in R$
are c-opposed and
![]() $\beta \neq -\gamma $
. Then:
$\beta \neq -\gamma $
. Then:
-
1.
 $(\beta ,\gamma ) = (\gamma ^{\vee },{\tilde {\beta }}) = (\beta ^{\vee },{\tilde {\gamma }}) = 0$
;
$(\beta ,\gamma ) = (\gamma ^{\vee },{\tilde {\beta }}) = (\beta ^{\vee },{\tilde {\gamma }}) = 0$
; -
2.
 $s_{\beta } s_{\gamma } =s_{\gamma } s_{\beta } \leq _R c^{-1}$
.
$s_{\beta } s_{\gamma } =s_{\gamma } s_{\beta } \leq _R c^{-1}$
.
Proof. We have
![]() $A_{i+h} = -A_i$
. Suppose that
$A_{i+h} = -A_i$
. Suppose that
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
are c-opposed. Then we may choose bipartite
$\gamma $
are c-opposed. Then we may choose bipartite
![]() $R^+$
so that
$R^+$
so that
![]() $\beta \in A_1$
and
$\beta \in A_1$
and
![]() $\gamma \in A_{1+h}$
. Then
$\gamma \in A_{1+h}$
. Then
![]() $\beta = \alpha _i$
and
$\beta = \alpha _i$
and
![]() $\gamma = -\alpha _j$
, where
$\gamma = -\alpha _j$
, where
![]() $i,j \in I_+$
. Since
$i,j \in I_+$
. Since
![]() $i,j$
are not adjacent,
$i,j$
are not adjacent,
![]() $(\beta ,\gamma )=0$
follows. Also,
$(\beta ,\gamma )=0$
follows. Also,
![]() ${\tilde {\beta }} = \omega _i$
and
${\tilde {\beta }} = \omega _i$
and
![]() ${\tilde {\gamma }} = -\omega _j$
, so (1) follows. (2) is also clear from (19.1).
${\tilde {\gamma }} = -\omega _j$
, so (1) follows. (2) is also clear from (19.1).
Proposition 19.9. Let
![]() $(R^+,c)$
be bipartite and
$(R^+,c)$
be bipartite and
![]() $\beta \prec _{R^+,c} \gamma $
be distinct positive roots. Then
$\beta \prec _{R^+,c} \gamma $
be distinct positive roots. Then
![]() $s_{\beta } s_{\gamma } \leq _R c^{-1}$
if and only if
$s_{\beta } s_{\gamma } \leq _R c^{-1}$
if and only if
![]() $\beta ,\gamma $
are alternating c-noncrossing.
$\beta ,\gamma $
are alternating c-noncrossing.
Proof. If
![]() $s_{\beta } s_{\gamma } \leq _R c^{-1}$
, then by Lemma 19.7, we have
$s_{\beta } s_{\gamma } \leq _R c^{-1}$
, then by Lemma 19.7, we have
![]() $(\beta ,\gamma ) \geq 0$
, and by Lemma 19.6, we have
$(\beta ,\gamma ) \geq 0$
, and by Lemma 19.6, we have
![]() $(\beta ^{\vee },{\tilde {\gamma }})=0$
. Thus,
$(\beta ^{\vee },{\tilde {\gamma }})=0$
. Thus,
![]() $(\beta ,\gamma )$
is alternating c-noncrossing.
$(\beta ,\gamma )$
is alternating c-noncrossing.
Conversely, suppose that
![]() $(\beta ,\gamma )$
is alternating and c-noncrossing. If
$(\beta ,\gamma )$
is alternating and c-noncrossing. If
![]() $(\beta ^{\vee },{\tilde {\gamma }}) =0$
, then by Lemma 19.6, we have
$(\beta ^{\vee },{\tilde {\gamma }}) =0$
, then by Lemma 19.6, we have
![]() $s_{\beta } s_{\gamma } \leq c^{-1}$
, and we are done. Next, suppose that we have
$s_{\beta } s_{\gamma } \leq c^{-1}$
, and we are done. Next, suppose that we have
![]() $(\gamma ^{\vee }, {\tilde {\beta }}) = 0$
. We claim that
$(\gamma ^{\vee }, {\tilde {\beta }}) = 0$
. We claim that
![]() $(\beta ,\gamma ) = 0$
. To see this, we assume that
$(\beta ,\gamma ) = 0$
. To see this, we assume that
![]() $R^+$
has been chosen so that
$R^+$
has been chosen so that
![]() $\beta \in A_1$
while
$\beta \in A_1$
while
![]() $\gamma \in \bigcup _{i=1}^h A_i$
. Thus,
$\gamma \in \bigcup _{i=1}^h A_i$
. Thus,
![]() $\beta = \alpha _i$
and
$\beta = \alpha _i$
and
![]() ${\tilde {\beta }}= \omega _i$
. The condition
${\tilde {\beta }}= \omega _i$
. The condition
![]() $(\gamma ^{\vee },\omega _i) = 0$
implies that
$(\gamma ^{\vee },\omega _i) = 0$
implies that
![]() $(\gamma ^{\vee },\alpha _i) \leq 0$
, and the alternating condition gives
$(\gamma ^{\vee },\alpha _i) \leq 0$
, and the alternating condition gives
![]() $(\gamma ^{\vee },\alpha _i) \geq 0$
. Thus,
$(\gamma ^{\vee },\alpha _i) \geq 0$
. Thus,
![]() $(\beta ,\gamma ) = 0$
, establishing our claim.
$(\beta ,\gamma ) = 0$
, establishing our claim.
We are thus in the situation that
![]() $(\gamma ^{\vee }, {\tilde {\beta }}) = 0$
and
$(\gamma ^{\vee }, {\tilde {\beta }}) = 0$
and
![]() $(\beta ,\gamma ) = 0$
. If
$(\beta ,\gamma ) = 0$
. If
![]() $\beta ,\gamma \in A_i$
for some i (that is, they are close together in the ordering), then by Lemma 19.16, we have
$\beta ,\gamma \in A_i$
for some i (that is, they are close together in the ordering), then by Lemma 19.16, we have
![]() $\prod _{\delta \in A_i}s_{\delta } \prod _{\delta ' \in A_{i+1}} s_{\delta '} = c^{-1}$
, so we know that
$\prod _{\delta \in A_i}s_{\delta } \prod _{\delta ' \in A_{i+1}} s_{\delta '} = c^{-1}$
, so we know that
![]() $s_{\beta } s_{\gamma } \leq c^{-1}$
, and we are done. Now, if
$s_{\beta } s_{\gamma } \leq c^{-1}$
, and we are done. Now, if
![]() $\beta \in A_i$
, then
$\beta \in A_i$
, then
![]() $-\beta \in A_{i+h}$
. Thus, we may find a different positive system
$-\beta \in A_{i+h}$
. Thus, we may find a different positive system
![]() $(R')^+$
, bipartite with respect to c, so that
$(R')^+$
, bipartite with respect to c, so that
![]() $\gamma \prec _{(R')^+,c} -\beta $
, and
$\gamma \prec _{(R')^+,c} -\beta $
, and
![]() $\gamma ,-\beta \in (R')^+$
. By Lemma 19.6, we have
$\gamma ,-\beta \in (R')^+$
. By Lemma 19.6, we have
![]() $s_{\gamma } s_{\beta } \leq c^{-1}$
, and since
$s_{\gamma } s_{\beta } \leq c^{-1}$
, and since
![]() $s_{\gamma } s_{\beta }= s_{\beta } s_{\gamma }$
, we are done.
$s_{\gamma } s_{\beta }= s_{\beta } s_{\gamma }$
, we are done.
Corollary 19.10. Suppose that
![]() $\beta ,\gamma $
are distinct roots, such that
$\beta ,\gamma $
are distinct roots, such that
![]() $\beta \neq -\gamma $
. Then the following are equivalent:
$\beta \neq -\gamma $
. Then the following are equivalent:
-
1.
 $\beta $
and
$\beta $
and
 $\gamma $
are c-noncrossing;
$\gamma $
are c-noncrossing; -
2. either
 $s_{\beta } s_{\gamma } \leq _R c^{-1}$
or
$s_{\beta } s_{\gamma } \leq _R c^{-1}$
or
 $s_{\gamma } s_{\beta } \leq _R c^{-1}$
.
$s_{\gamma } s_{\beta } \leq _R c^{-1}$
.
Proof. Suppose (1) holds. Replacing
![]() $\gamma $
by
$\gamma $
by
![]() $-\gamma $
does not change either of the conditions (1) or (2). Thus, we may assume that
$-\gamma $
does not change either of the conditions (1) or (2). Thus, we may assume that
![]() $\beta , \gamma $
are alternating c-noncrossing. If
$\beta , \gamma $
are alternating c-noncrossing. If
![]() $\beta ,\gamma $
are c-opposed, we apply Lemma 19.8. Otherwise, we pick any bipartite
$\beta ,\gamma $
are c-opposed, we apply Lemma 19.8. Otherwise, we pick any bipartite
![]() $R^+$
containing
$R^+$
containing
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
and apply Proposition 19.9.
$\gamma $
and apply Proposition 19.9.
Conversely, suppose (2) holds, for concreteness, let us assume that
![]() $s_{\beta } s_{\gamma } \leq _R c^{-1}$
. If
$s_{\beta } s_{\gamma } \leq _R c^{-1}$
. If
![]() $\beta ,\gamma $
are c-opposed, we apply Lemma 19.8. Otherwise, we can find
$\beta ,\gamma $
are c-opposed, we apply Lemma 19.8. Otherwise, we can find
![]() $R^+$
, such that either
$R^+$
, such that either
![]() $\beta \prec _{R^+,c} \gamma $
are both positive roots, or
$\beta \prec _{R^+,c} \gamma $
are both positive roots, or
![]() $-\beta \prec _{R^+,c} \gamma $
are both positive roots. By Proposition 19.9, in both cases, (2) holds.
$-\beta \prec _{R^+,c} \gamma $
are both positive roots. By Proposition 19.9, in both cases, (2) holds.
19.4. Cluster compatibility and Coxeter noncrossing
Let
denote the set of almost simple roots. The notion of (cluster) compatibility of a pair of almost simple roots
![]() $\beta ,\beta ' \in R_{\geq -1}$
is defined in [Reference Fomin and ZelevinskyFZ03], and it is related to the notion of compatibility of a pair
$\beta ,\beta ' \in R_{\geq -1}$
is defined in [Reference Fomin and ZelevinskyFZ03], and it is related to the notion of compatibility of a pair
![]() $\omega ,\omega ' \in \Pi (c)$
by [Reference Yang and ZelevinskyYZ, (5.6)]. Namely, let
$\omega ,\omega ' \in \Pi (c)$
by [Reference Yang and ZelevinskyYZ, (5.6)]. Namely, let
![]() $\psi : \Pi (c) \to R_{\geq -1}$
be defined by
$\psi : \Pi (c) \to R_{\geq -1}$
be defined by
 $$ \begin{align} \psi(\omega) = \begin{cases} -\alpha_i & \mbox{if } \omega = \omega_i \mbox{ for some } i=1,2,\ldots,r \\ c^{-1} \omega - \omega = c^{-1} (I-c) \omega & \mbox{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} \psi(\omega) = \begin{cases} -\alpha_i & \mbox{if } \omega = \omega_i \mbox{ for some } i=1,2,\ldots,r \\ c^{-1} \omega - \omega = c^{-1} (I-c) \omega & \mbox{otherwise.} \end{cases} \end{align} $$
Then
Theorem 19.11 [Reference Brady and WattBW, Theorem 8.3]
Suppose that
![]() $\beta \prec _{R^+,c} \gamma $
are two distinct positive roots. Then
$\beta \prec _{R^+,c} \gamma $
are two distinct positive roots. Then
![]() $(\beta ,\gamma )$
are
$(\beta ,\gamma )$
are
![]() $(W,R^+,c)$
-compatible if and only if
$(W,R^+,c)$
-compatible if and only if
![]() $s_{\beta } s_{\gamma } \leq _R c^{-1}$
.
$s_{\beta } s_{\gamma } \leq _R c^{-1}$
.
Proposition 19.12. Suppose that
![]() $(R^+,c)$
is bipartite and
$(R^+,c)$
is bipartite and
![]() $\beta ,\gamma \in R^+.$
Then
$\beta ,\gamma \in R^+.$
Then
![]() $(\beta ,\gamma )$
is alternating c-noncrossing if and only if they are
$(\beta ,\gamma )$
is alternating c-noncrossing if and only if they are
![]() $(W,R^+,c)$
-compatible.
$(W,R^+,c)$
-compatible.
Proof. Let us suppose that
![]() $\beta \prec \gamma $
. By Theorem 19.11, we must show that
$\beta \prec \gamma $
. By Theorem 19.11, we must show that
![]() $\beta ,\gamma $
are alternating c-noncrossing if and only if
$\beta ,\gamma $
are alternating c-noncrossing if and only if
![]() $s_{\beta } s_{\gamma } \leq _R c^{-1}$
. This follows from Proposition 19.9.
$s_{\beta } s_{\gamma } \leq _R c^{-1}$
. This follows from Proposition 19.9.
Proposition 19.12 says that the condition “alternating and c-noncrossing” is an approximation to the notion of cluster compatibility that does not depend on a choice of
![]() $R^+$
.
$R^+$
.
19.5. Coxeter noncrossing trees
An r-tuple
![]() $T=(\gamma _1,\ldots ,\gamma _r)$
of roots is called a tree if they form a basis of V.
$T=(\gamma _1,\ldots ,\gamma _r)$
of roots is called a tree if they form a basis of V.
Definition 19.13. A c-noncrossing tree is an ordered sequence
![]() $T=(\gamma _1,\ldots ,\gamma _r)$
of roots, such that
$T=(\gamma _1,\ldots ,\gamma _r)$
of roots, such that
Let
![]() ${\mathcal {T}}_{W,c}$
denote the set of c-noncrossing trees.
${\mathcal {T}}_{W,c}$
denote the set of c-noncrossing trees.
The terminology is justified by the following result.
Lemma 19.14. A c-noncrossing tree
![]() $T=(\gamma _1,\ldots ,\gamma _r)$
is an ordered basis of V.
$T=(\gamma _1,\ldots ,\gamma _r)$
is an ordered basis of V.
Proof. Suppose the roots
![]() $\gamma _1,\ldots ,\gamma _r$
span a proper subspace
$\gamma _1,\ldots ,\gamma _r$
span a proper subspace
![]() $W \subsetneq V$
. Then any vector in the orthogonal complement
$W \subsetneq V$
. Then any vector in the orthogonal complement
![]() $W^{\perp } \subset V$
(with respect to
$W^{\perp } \subset V$
(with respect to
![]() $(\cdot ,\cdot )$
) will be invariant under
$(\cdot ,\cdot )$
) will be invariant under
![]() $c^{-1}$
. This contradicts the fact that
$c^{-1}$
. This contradicts the fact that
![]() $c^{-1}$
does not have the eigenvalue one (see Lemma 10.2).
$c^{-1}$
does not have the eigenvalue one (see Lemma 10.2).
Remark 19.15. For a c-noncrossing tree
![]() $T=(\gamma _1,\ldots ,\gamma _r)$
, define the operation of i-th sign reversal
$T=(\gamma _1,\ldots ,\gamma _r)$
, define the operation of i-th sign reversal
and the operation of j-th conjugation
These operations transform c-noncrossing trees into c-noncrossing trees. It follows from the results of Deligne [Reference DeligneDel] and Bessis [Reference BessisBes] that any two c-noncrossing trees are related by repeated application of sign reversal and conjugation. Furthermore, the conjugation actions give an action of the braid group.
Lemma 19.16. Let
![]() $(\beta _1,\beta _2,\ldots ,\beta _{hr})$
denote the ordering of R of Proposition 10.3. Then for any i, we have that
$(\beta _1,\beta _2,\ldots ,\beta _{hr})$
denote the ordering of R of Proposition 10.3. Then for any i, we have that
![]() $(\beta _i,\beta _{i+1},\ldots ,\beta _{i+r-1})$
is a c-noncrossing tree.
$(\beta _i,\beta _{i+1},\ldots ,\beta _{i+r-1})$
is a c-noncrossing tree.
Proof. By Proposition 10.4, it suffices to show this for
![]() $i = 1$
. Suppose
$i = 1$
. Suppose
![]() $c = s_1s_2 \cdots s_r$
. We calculate
$c = s_1s_2 \cdots s_r$
. We calculate
According to Corollary 19.10, the “c-noncrossing” condition characterizes when a pair of roots can belong to a c-noncrossing tree. However, in general, this pairwise condition is insufficient to characterize c-noncrossing trees.
Example 19.17. Let
![]() $R = B_3$
with simple roots
$R = B_3$
with simple roots
![]() $\alpha _1 = (1,-1,0)$
,
$\alpha _1 = (1,-1,0)$
,
![]() $\alpha _2 = (0,1,-1)$
, and
$\alpha _2 = (0,1,-1)$
, and
![]() $\alpha _3 = (0,0,1)$
, and choose
$\alpha _3 = (0,0,1)$
, and choose
![]() $c = s_1s_2s_3$
, as in Example 10.9. Take the three roots
$c = s_1s_2s_3$
, as in Example 10.9. Take the three roots
with corresponding c-twisted roots
The roots
![]() $\gamma _1,\gamma _2,\gamma _3$
are pairwise c-noncrossing (and also alternating). However, all three roots are long, so no ordering of them can give a reflection factorization of
$\gamma _1,\gamma _2,\gamma _3$
are pairwise c-noncrossing (and also alternating). However, all three roots are long, so no ordering of them can give a reflection factorization of
![]() $c^{-1}$
.
$c^{-1}$
.
Definition 19.18. Let
![]() $T=(\gamma _1,\ldots ,\gamma _r)$
be a c-noncrossing tree. Then the dual tree
$T=(\gamma _1,\ldots ,\gamma _r)$
be a c-noncrossing tree. Then the dual tree
![]() $T' = \varphi (T) $
is given by
$T' = \varphi (T) $
is given by
Also, define
![]() $T" = \varphi ^{-1}(T)$
by
$T" = \varphi ^{-1}(T)$
by
Proposition 19.19. Let T be a c-noncrossing tree. Then the trees
![]() $T' = \varphi (T)$
and
$T' = \varphi (T)$
and
![]() $T" = \varphi ^{-1}(T)$
are c-noncrossing tree. The maps
$T" = \varphi ^{-1}(T)$
are c-noncrossing tree. The maps
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi ^{-1}$
are inverse bijections from
$\varphi ^{-1}$
are inverse bijections from
![]() ${\mathcal {T}}_{W,c}$
to
${\mathcal {T}}_{W,c}$
to
![]() ${\mathcal {T}}_{W,c}$
.
${\mathcal {T}}_{W,c}$
.
Proof. Let
![]() $T = (\gamma _1,\ldots ,\gamma _r)$
and
$T = (\gamma _1,\ldots ,\gamma _r)$
and
![]() $T' = (\gamma ^{\prime }_1,\ldots ,\gamma ^{\prime }_r)$
. We have
$T' = (\gamma ^{\prime }_1,\ldots ,\gamma ^{\prime }_r)$
. We have
The proof for
![]() $T"$
is similar, and it is straightforward to see that
$T"$
is similar, and it is straightforward to see that
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi ^{-1}$
are inverse.
$\varphi ^{-1}$
are inverse.
For a tree
![]() $T=(\gamma _1,\ldots ,\gamma _r)$
, let
$T=(\gamma _1,\ldots ,\gamma _r)$
, let
![]() $C_T \subset V$
denote the cone spanned by
$C_T \subset V$
denote the cone spanned by
![]() ${\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r$
, and let
${\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r$
, and let
![]() $C^{\prime }_T \subset V$
denote the cone spanned by
$C^{\prime }_T \subset V$
denote the cone spanned by
![]() $\gamma _1^{\vee },\ldots ,\gamma _r^{\vee }$
. The following result is a general root-system theoretic version of Proposition 8.15.
$\gamma _1^{\vee },\ldots ,\gamma _r^{\vee }$
. The following result is a general root-system theoretic version of Proposition 8.15.
Proposition 19.20. Let T be a c-noncrossing tree and
![]() $T' = \varphi (T)$
. Then the two cones
$T' = \varphi (T)$
. Then the two cones
![]() $C_T$
and
$C_T$
and
![]() $C^{\prime }_{T'}$
are dual.
$C^{\prime }_{T'}$
are dual.
Proof. Let
![]() $T' = (\delta _1,\ldots ,\delta _r)$
, and let
$T' = (\delta _1,\ldots ,\delta _r)$
, and let
![]() $\kappa _1,\kappa _2,\ldots ,\kappa _r$
be the dual basis to
$\kappa _1,\kappa _2,\ldots ,\kappa _r$
be the dual basis to
![]() $\delta _1^{\vee },\ldots ,\delta _r^{\vee }$
, that is,
$\delta _1^{\vee },\ldots ,\delta _r^{\vee }$
, that is,
![]() $(\delta _i^{\vee },\kappa _j) = \delta _{ij}$
. Then
$(\delta _i^{\vee },\kappa _j) = \delta _{ij}$
. Then
Thus,
![]() $(I-c)\kappa _j = s_{\delta _r} \cdots s_{\delta _{j+1}} \delta _j$
, so the dual cone to
$(I-c)\kappa _j = s_{\delta _r} \cdots s_{\delta _{j+1}} \delta _j$
, so the dual cone to
![]() $C^{\prime }_{T'}$
is given by
$C^{\prime }_{T'}$
is given by
![]() $C_{\varphi ^{-1}(T')}$
.
$C_{\varphi ^{-1}(T')}$
.
Corollary 19.21. Suppose that P is a simple
![]() $(W,c)$
-twisted alcoved polytope, and all maximal cones of the normal fan of P are of the form
$(W,c)$
-twisted alcoved polytope, and all maximal cones of the normal fan of P are of the form
![]() $C_T$
for a c-noncrossing tree T. Then P is a generalized W-permutohedron and thus a
$C_T$
for a c-noncrossing tree T. Then P is a generalized W-permutohedron and thus a
![]() $(W,c)$
-polypositroid.
$(W,c)$
-polypositroid.
Question 19.22. Let P be a generic simple
![]() $(W,c)$
-polypositroid. Are all maximal cones of the normal fan of P of the form
$(W,c)$
-polypositroid. Are all maximal cones of the normal fan of P of the form
![]() $C_T$
for a c-noncrossing tree T?
$C_T$
for a c-noncrossing tree T?
Question 19.22 has an affirmative answer in type A (see Section 19.7).
19.6. Cluster cones
A
![]() $(W,c)$
-cluster cone is a maximal cone
$(W,c)$
-cluster cone is a maximal cone
![]() $C \subset V$
in the
$C \subset V$
in the
![]() $(W,R^+,c)$
-cluster fan, for some choice of positive roots
$(W,R^+,c)$
-cluster fan, for some choice of positive roots
![]() $R^+ \subset R$
. It follows from the results of Brady-Watt [Reference Brady and WattBW] that some cluster cones are of the form
$R^+ \subset R$
. It follows from the results of Brady-Watt [Reference Brady and WattBW] that some cluster cones are of the form
![]() $C_T$
for a c-noncrossing tree T, though we do not know whether this is true in general.
$C_T$
for a c-noncrossing tree T, though we do not know whether this is true in general.
Proposition 19.23. Suppose that
![]() $(R^+,c)$
is bipartite. Let
$(R^+,c)$
is bipartite. Let
![]() $C =\mathrm {span}({\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r)$
be a cluster cone, such that
$C =\mathrm {span}({\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r)$
be a cluster cone, such that
![]() $\{{\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r\} \cap \{\omega _1,\ldots ,\omega _r\} = \emptyset $
. Then there is an ordering of
$\{{\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r\} \cap \{\omega _1,\ldots ,\omega _r\} = \emptyset $
. Then there is an ordering of
![]() $({\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r)$
that gives a c-noncrossing tree T.
$({\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r)$
that gives a c-noncrossing tree T.
Proof. As a simplicial complex on the set of rays, the
![]() $(W,R^+,c)$
-cluster fan is isomorphic, via the bijection (19.2) to the cluster complex of [Reference Fomin and ZelevinskyFZ03] defined on the set of almost positive roots
$(W,R^+,c)$
-cluster fan is isomorphic, via the bijection (19.2) to the cluster complex of [Reference Fomin and ZelevinskyFZ03] defined on the set of almost positive roots
![]() $R_{\geq -1}$
. The condition
$R_{\geq -1}$
. The condition
![]() $\{{\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r\} \cap \{\omega _1,\ldots ,\omega _r\} = \emptyset $
is equivalent to the condition that the almost positive roots
$\{{\tilde {\gamma }}_1,\ldots ,{\tilde {\gamma }}_r\} \cap \{\omega _1,\ldots ,\omega _r\} = \emptyset $
is equivalent to the condition that the almost positive roots
![]() $\psi ({\tilde {\gamma }}_i)$
are positive.
$\psi ({\tilde {\gamma }}_i)$
are positive.
According to [Reference Brady and WattBW, Note 4.2 and Theorem 8.3], a sequence
![]() $\delta _1 \prec \delta _2 \cdots \prec \delta _r$
of positive roots forms a simplex in the cluster complex if and only if
$\delta _1 \prec \delta _2 \cdots \prec \delta _r$
of positive roots forms a simplex in the cluster complex if and only if
![]() $(\delta _1,\ldots ,\delta _r)$
is a c-noncrossing tree. The claim follows.
$(\delta _1,\ldots ,\delta _r)$
is a c-noncrossing tree. The claim follows.
Remark 19.24. Reading and Speyer [Reference Reading and SpeyerRS] have found a linear isomorphism from the cluster fan of [Reference Fomin and ZelevinskyFZ03] (with rays the almost positive roots), to the
![]() $(W,R^+,c)$
-cluster fan, called the g-vector fan in [Reference Reading and SpeyerRS].
$(W,R^+,c)$
-cluster fan, called the g-vector fan in [Reference Reading and SpeyerRS].
19.7. Type A
We make explicit the relation between reflection factorizations of
![]() $c^{-1}$
and noncrossing trees (in type A).
$c^{-1}$
and noncrossing trees (in type A).
Lemma 19.25. Let T be a noncrossing (undirected) tree on
![]() $[n]$
. Then there is an ordering
$[n]$
. Then there is an ordering
![]() $e_1,\ldots ,e_{n-1}$
of the edges so that
$e_1,\ldots ,e_{n-1}$
of the edges so that
![]() $s_{e_1} \cdots s_{e_{n-1}} = c = (12\cdots n)$
. Varying the possible orderings gives the same reduced factorization of c up to commutation relations.
$s_{e_1} \cdots s_{e_{n-1}} = c = (12\cdots n)$
. Varying the possible orderings gives the same reduced factorization of c up to commutation relations.
Proof. Let us draw T in the interior of a disk with the vertices arranged in clockwise order on the boundary. Let
![]() $f^{(i)}_1,f^{(i)}_2,\ldots ,f^{(i)}_s$
be edges incident to the vertex i, in counterclockwise order. An ordering
$f^{(i)}_1,f^{(i)}_2,\ldots ,f^{(i)}_s$
be edges incident to the vertex i, in counterclockwise order. An ordering
![]() $e_1,\ldots ,e_{n-1}$
of all the edges of T satisfies
$e_1,\ldots ,e_{n-1}$
of all the edges of T satisfies
![]() $s_{e_1} \cdots s_{e_{n-1}} = c$
if and only if
$s_{e_1} \cdots s_{e_{n-1}} = c$
if and only if
![]() $\{f^{(i)}_1,\ldots ,f^{(i)}_s\}$
appear in the same order in
$\{f^{(i)}_1,\ldots ,f^{(i)}_s\}$
appear in the same order in
![]() $e_1,\ldots ,e_{n-1}$
for any vertex i. Since T contains no cycles, it is not difficult to see that such an ordering
$e_1,\ldots ,e_{n-1}$
for any vertex i. Since T contains no cycles, it is not difficult to see that such an ordering
![]() $e_1,\ldots ,e_{n-1}$
exists. The last statement follows from:
$e_1,\ldots ,e_{n-1}$
exists. The last statement follows from:
![]() $s_e$
and
$s_e$
and
![]() $s_{e'}$
commute if they have no vertex in common.
$s_{e'}$
commute if they have no vertex in common.
Example 19.26. Let T be the (solid) tree of Figure 2, with the five edges
Then around the vertices
![]() $2$
,
$2$
,
![]() $4$
, and
$4$
, and
![]() $6$
, we obtain the counterclockwise orderings
$6$
, we obtain the counterclockwise orderings
One may check that
consistent with Lemma 19.25.
Part III Membranes
In this part, we discuss membranes, which are certain triangulated 2-dimensional surfaces embedded into
![]() $\mathbb {R}^n$
. They can be viewed as a polypositroidal version of the plabic graphs from [Reference PostnikovPo06].
$\mathbb {R}^n$
. They can be viewed as a polypositroidal version of the plabic graphs from [Reference PostnikovPo06].
20. Root loops and root membranes
Let R be an irreducible reduced crystallographic root system of rank r in a Euclidean vector space
![]() $V\simeq \mathbb {R}^r$
. We identify the weight lattice
$V\simeq \mathbb {R}^r$
. We identify the weight lattice
![]() $\Lambda \subset V$
with
$\Lambda \subset V$
with
![]() $\Lambda \simeq \mathbb {Z}^r$
(see Section 10.1).
$\Lambda \simeq \mathbb {Z}^r$
(see Section 10.1).
Definition 20.1. A plane graph is a planar graph with a particular drawing on the plane without crossing edges, considered up to a homeomorphism.
A cactus G is a finite connected undirected plane graph with at least two vertices, such that every face of G (except the outer face) is a triangle, that is, every face has exactly three distinct vertices connected by three edges. In other words, a cactus is either a single edge, a triangulated disk, or a wedge of smaller cacti along their boundary vertices.
If a cactus G is a wedge of smaller cacti, then we say that G is decomposable. Otherwise, we say that G is indecomposable.
For a cactus G, there is a unique (up to a cyclic shift) sequence
![]() $B=(b_1,\dots ,b_m)$
of boundary vertices connected by boundary edges
$B=(b_1,\dots ,b_m)$
of boundary vertices connected by boundary edges
![]() $\{b_1,b_2\}$
,
$\{b_1,b_2\}$
,
![]() $\{b_2,b_3\}$
, …,
$\{b_2,b_3\}$
, …,
![]() $\{b_m,b_1\}$
obtained by walking along the boundary of G in the clockwise direction.
$\{b_m,b_1\}$
obtained by walking along the boundary of G in the clockwise direction.
An example of a (decomposable) cactus G is shown in Figure 5.
Remark 20.2. If G is a decomposable cactus, then the sequence B has repeated entries. The way a cactus decomposes into indecomposable cacti is given by a noncrossing set partition of
![]() $[m]$
without singleton blocks. Blocks of this noncrossing set partition correspond to boundary vertices of connected components of the dual plane graph
$[m]$
without singleton blocks. Blocks of this noncrossing set partition correspond to boundary vertices of connected components of the dual plane graph
![]() $G^*$
, cf. Remark 21.3.
$G^*$
, cf. Remark 21.3.
Definition 20.3. (1) An R-loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is a sequence of weights
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is a sequence of weights
![]() $\lambda ^{(a)}\in \Lambda $
, cyclically indexed by elements
$\lambda ^{(a)}\in \Lambda $
, cyclically indexed by elements
![]() $a\in \mathbb {Z}/m\mathbb {Z}$
, such that
$a\in \mathbb {Z}/m\mathbb {Z}$
, such that
![]() $\lambda ^{(a+1)}-\lambda ^{(a)}\in R$
, for any
$\lambda ^{(a+1)}-\lambda ^{(a)}\in R$
, for any
![]() $a\in \mathbb {Z}/m\mathbb {Z}$
.
$a\in \mathbb {Z}/m\mathbb {Z}$
.
(2) An R-membrane
![]() $M=(G,\mathit {f})$
with boundary loop
$M=(G,\mathit {f})$
with boundary loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is a cactus G on a vertex set
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is a cactus G on a vertex set
![]() ${\mathrm {Vert}}$
with the sequence of boundary edges
${\mathrm {Vert}}$
with the sequence of boundary edges
![]() $B=(b_1,\dots ,b_m)$
together with a (not necessarily injective) embedding map
$B=(b_1,\dots ,b_m)$
together with a (not necessarily injective) embedding map
![]() $\mathit {f}:{\mathrm {Vert}}\to \Lambda $
, such that,
$\mathit {f}:{\mathrm {Vert}}\to \Lambda $
, such that,
-
○
 $\mathit {f}(u)-\mathit {f}(v)\in R$
, for any edge
$\mathit {f}(u)-\mathit {f}(v)\in R$
, for any edge
 $\{u,v\}$
of G, and
$\{u,v\}$
of G, and -
○
 $\mathit {f}(b_a)= \lambda ^{(a)}$
, for any
$\mathit {f}(b_a)= \lambda ^{(a)}$
, for any
 $a\in \mathbb {Z}/m\mathbb {Z}$
$a\in \mathbb {Z}/m\mathbb {Z}$
(in particular, we require that
![]() $f(u)\ne f(v)$
for any edge
$f(u)\ne f(v)$
for any edge
![]() $\{u,v\}$
of G).
$\{u,v\}$
of G).
Equivalently, an R-membrane is a cactus G together with a graph homomorphismFootnote 3 f from G to the graph on the vertex set
![]() $\Lambda $
with edges
$\Lambda $
with edges
![]() $\{\lambda ,\mu \}$
for
$\{\lambda ,\mu \}$
for
![]() $\lambda -\mu \in R$
.
$\lambda -\mu \in R$
.
(3) An R-line segment is a line segment
![]() $\mathrm {conv}(\lambda ,\mu )\subset V$
, where
$\mathrm {conv}(\lambda ,\mu )\subset V$
, where
![]() $\lambda -\mu \in R$
and an R-triangle is a triangle
$\lambda -\mu \in R$
and an R-triangle is a triangle
![]() $\mathrm {conv}(\lambda ,\mu ,\nu )\subset V$
, where
$\mathrm {conv}(\lambda ,\mu ,\nu )\subset V$
, where
![]() $\lambda ,\mu ,\nu \in \Lambda $
, such that
$\lambda ,\mu ,\nu \in \Lambda $
, such that
![]() $\lambda -\mu ,\mu -\nu ,\nu -\lambda \in R$
.
$\lambda -\mu ,\mu -\nu ,\nu -\lambda \in R$
.
Example 20.4. The sequence
![]() $L = (\omega _1, \omega _2-\omega _1, \omega _3 - \omega _1, \omega _3, 2\omega _4, \omega _1 + \omega _3-\omega _2)$
is a
$L = (\omega _1, \omega _2-\omega _1, \omega _3 - \omega _1, \omega _3, 2\omega _4, \omega _1 + \omega _3-\omega _2)$
is a
![]() $B_4$
-loop, in the notation of Examples 10.9 and 16.3. Let G have boundary vertices
$B_4$
-loop, in the notation of Examples 10.9 and 16.3. Let G have boundary vertices
![]() $b_1,b_2,b_3,b_4,b_5,b_6$
arranged clockwise, interior vertex b, and triangular (clockwise-oriented) faces
$b_1,b_2,b_3,b_4,b_5,b_6$
arranged clockwise, interior vertex b, and triangular (clockwise-oriented) faces
![]() $(b,b_1,b_2), (b,b_2,b_3), (b,b_3,b_6), (b,b_6,b_1),(b_3,b_4,b_6),(b_4,b_5,b_6)$
. Let
$(b,b_1,b_2), (b,b_2,b_3), (b,b_3,b_6), (b,b_6,b_1),(b_3,b_4,b_6),(b_4,b_5,b_6)$
. Let
![]() $\mathit {f}(b_i) = \lambda ^{(i)}$
and
$\mathit {f}(b_i) = \lambda ^{(i)}$
and
![]() $\mathit {f}(b) = \omega _3-\omega _2$
. Then
$\mathit {f}(b) = \omega _3-\omega _2$
. Then
![]() $(G,\mathit {f})$
is a
$(G,\mathit {f})$
is a
![]() $B_4$
-membrane.
$B_4$
-membrane.
An R-loop L can be viewed as a closed piecewise-linear curve
![]() $\left <L\right>$
in V, and R-membranes M with boundary loop L can be viewed as 2-dimensional simplicial complexes embedded into V as surfaces
$\left <L\right>$
in V, and R-membranes M with boundary loop L can be viewed as 2-dimensional simplicial complexes embedded into V as surfaces
![]() $\left <M\right>$
composed of R-triangles and R-line segments with a given boundary curve
$\left <M\right>$
composed of R-triangles and R-line segments with a given boundary curve
![]() $\left <L\right>$
, as follows.
$\left <L\right>$
, as follows.
For an R-loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
, let
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
, let
![]() $\left <L\right>\subset V$
be the closed piecewise-linear curve given by the union of R-line segments
$\left <L\right>\subset V$
be the closed piecewise-linear curve given by the union of R-line segments
Let
![]() $M=(G,\mathit {f})$
be an R-membrane with boundary loop L. For a face
$M=(G,\mathit {f})$
be an R-membrane with boundary loop L. For a face
![]() $\Delta $
of G with vertices
$\Delta $
of G with vertices
![]() $u,v,w$
, let
$u,v,w$
, let
![]() $\left <\Delta \right>:=\mathrm {conv}(\mathit {f}(u),\mathit {f}(v),\mathit {f}(w))\subset V$
be the corresponding R-triangle. The triangulated surface
$\left <\Delta \right>:=\mathrm {conv}(\mathit {f}(u),\mathit {f}(v),\mathit {f}(w))\subset V$
be the corresponding R-triangle. The triangulated surface
![]() $\left <M\right>\subset V$
associated with the membrane M is given by the union
$\left <M\right>\subset V$
associated with the membrane M is given by the union
Definition 20.5. Let
![]() $\mathrm {val}:\{\textrm {\(R\)-triangles}\}\to \mathbb {R}_{>0}$
be any positive real function, or valuation,Footnote 4 on the set of all R-triangles. We say that an R-membrane M with boundary loop L is minimal, with respect to the valuation
$\mathrm {val}:\{\textrm {\(R\)-triangles}\}\to \mathbb {R}_{>0}$
be any positive real function, or valuation,Footnote 4 on the set of all R-triangles. We say that an R-membrane M with boundary loop L is minimal, with respect to the valuation
![]() $\mathrm {val}$
, if its surface area
$\mathrm {val}$
, if its surface area
has minimal possible value among all membranes with the same boundary loop L.
Remark 20.6. Our membranes should not to be confused with those of Keel and Tevelev [Reference Keel and TevelevKeTe] appearing in the study of the Chow quotient of the Grassmannian.
Remark 20.7. The famous Plateau’s problem originally raised by Lagrange is the problem in geometric measure theory concerning the existence of a minimal surface with a given boundary. It was solved by Jesse Douglas [Reference DouglasDou] and Tibor Radó [Reference RadóRad]. We view the problem about characterization of minimal membranes M with a given boundary loop L as a discrete version of Plateau’s problem. Unlike the situation with its continuous counterpart, the existence of a minimal membrane is trivial. There can be many minimal membranes with a given boundary. However, we think that the characterization of minimal membranes might provide a better understanding of the continuous Plateau’s problem.
21. Membranes of type A
Let us now specialize the definitions from the previous section to type
![]() $A $
. Let
$A $
. Let
be the
![]() $A_{n-1}$
root system embedded in
$A_{n-1}$
root system embedded in
![]() $\mathbb {R}^n$
, and let
$\mathbb {R}^n$
, and let
![]() $\Lambda \simeq \mathbb {Z}^n \subset \mathbb {R}^n$
. These are the root and weight lattices of
$\Lambda \simeq \mathbb {Z}^n \subset \mathbb {R}^n$
. These are the root and weight lattices of
![]() $\mathrm {GL}(n)$
. Recall that
$\mathrm {GL}(n)$
. Recall that
![]() $e_1,\ldots ,e_n$
denote the standard coordinate vectors in
$e_1,\ldots ,e_n$
denote the standard coordinate vectors in
![]() $\mathbb {Z}^n$
. We assume the valuationFootnote 5 of any R-triangle is
$\mathbb {Z}^n$
. We assume the valuationFootnote 5 of any R-triangle is
![]() $\mathrm {val} \left <\Delta \right>=1$
.
$\mathrm {val} \left <\Delta \right>=1$
.
In this case, we call R-loops and R-membranes simply loops and membranes. Let us formulate their definitions.
Definition 21.1. A loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is a cyclically ordered sequence of integer vectors
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is a cyclically ordered sequence of integer vectors
![]() $\lambda ^{(a)}\in \mathbb {Z}^n$
, such that
$\lambda ^{(a)}\in \mathbb {Z}^n$
, such that
![]() $\lambda ^{(a+1)}-\lambda ^{(a)} = e_{i_a}-e_{j_a}$
, for
$\lambda ^{(a+1)}-\lambda ^{(a)} = e_{i_a}-e_{j_a}$
, for
![]() $a\in \mathbb {Z}/m\mathbb {Z}$
, for some sequence of roots
$a\in \mathbb {Z}/m\mathbb {Z}$
, for some sequence of roots
![]() $e_{i_1}-e_{j_1},\ldots ,e_{i_m}-e_{j_m}$
.
$e_{i_1}-e_{j_1},\ldots ,e_{i_m}-e_{j_m}$
.
A membrane
![]() $M=(G,\mathit {f})$
with boundary loop
$M=(G,\mathit {f})$
with boundary loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is a cactus G on a vertex set
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is a cactus G on a vertex set
![]() ${\mathrm {Vert}}$
with the sequence of boundary vertices
${\mathrm {Vert}}$
with the sequence of boundary vertices
![]() $B=(b_1,\dots ,b_m)$
together with a map
$B=(b_1,\dots ,b_m)$
together with a map
![]() $f:{\mathrm {Vert}} \to \mathbb {Z}^{n}$
, such that
$f:{\mathrm {Vert}} \to \mathbb {Z}^{n}$
, such that
-
○ for any edge
 $\{u,v\}$
of G, there exists indices
$\{u,v\}$
of G, there exists indices
 $i\ne j$
, such that
$i\ne j$
, such that
 $\mathit {f}(u)-\mathit {f}(v) = e_i - e_j$
,
$\mathit {f}(u)-\mathit {f}(v) = e_i - e_j$
, -
○
 $\mathit {f}(b_a)=\lambda ^{(a)}$
, for any
$\mathit {f}(b_a)=\lambda ^{(a)}$
, for any
 $a\in \mathbb {Z}/m\mathbb {Z}$
.
$a\in \mathbb {Z}/m\mathbb {Z}$
.
Let
![]() $\left <L\right>, \left <M\right>\subset \mathbb {R}^n$
denote the images of a loop L and a membrane M in
$\left <L\right>, \left <M\right>\subset \mathbb {R}^n$
denote the images of a loop L and a membrane M in
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
Note that here we do not require m and n to be equal. Also note that the embedding
![]() $\left <M\right>\subset \mathbb {R}^n$
of a membrane lies on some affine hyperplane
$\left <M\right>\subset \mathbb {R}^n$
of a membrane lies on some affine hyperplane
![]() $H=H_k := \{(x_1,\dots ,x_n)\in \mathbb {R}^n\mid x_1+\cdots + x_n =k\}$
, where
$H=H_k := \{(x_1,\dots ,x_n)\in \mathbb {R}^n\mid x_1+\cdots + x_n =k\}$
, where
![]() ${k\in \mathbb {Z}}$
. Clearly, a loop L is determined (up to affine translation) by a sequence of roots
${k\in \mathbb {Z}}$
. Clearly, a loop L is determined (up to affine translation) by a sequence of roots
![]() $e_{i_1}-e_{j_1},\ldots ,e_{i_m}-e_{j_m}$
with equal multisets of indices
$e_{i_1}-e_{j_1},\ldots ,e_{i_m}-e_{j_m}$
with equal multisets of indices
![]() $\{i_1,\dots ,i_m\}=\{j_1,\dots ,j_m\}$
.
$\{i_1,\dots ,i_m\}=\{j_1,\dots ,j_m\}$
.
All faces
![]() $\Delta $
in a membrane are of one of the following two types:
$\Delta $
in a membrane are of one of the following two types:
-
○ black triangles embedded into
 $\mathbb {R}^n$
as triangles
$\mathbb {R}^n$
as triangles
 $\left <\Delta \right>$
of the form
$\left <\Delta \right>$
of the form
 $\mathrm {conv}(-e_i,-e_j,-e_k)$
, up to an affine translation; and
$\mathrm {conv}(-e_i,-e_j,-e_k)$
, up to an affine translation; and -
○ white triangles embedded as triangles
 $\left <\Delta \right>$
of the form
$\left <\Delta \right>$
of the form
 $\mathrm {conv}(e_i,e_j,e_k)$
, up to an affine translation.
$\mathrm {conv}(e_i,e_j,e_k)$
, up to an affine translation.
For a membrane
![]() $M=(G,f)$
, let
$M=(G,f)$
, let
![]() $G^*$
be the graph, which is the plane dual of the cactus G. The graph
$G^*$
be the graph, which is the plane dual of the cactus G. The graph
![]() $G^*$
is drawn in a disk so that
$G^*$
is drawn in a disk so that
-
1. There are m marked points on the boundary of the disk (labelled
 $1,\dots ,m$
clockwise) to which boundary edges of
$1,\dots ,m$
clockwise) to which boundary edges of
 $G^*$
are attached. Only one edge of
$G^*$
are attached. Only one edge of
 $G^*$
can be attached to a marked point on the disk. But it is allowed that both ends of an edge are attached to two different marked points on the boundary. (The marked point on the boundary of the disk labelled a corresponds to the boundary edge
$G^*$
can be attached to a marked point on the disk. But it is allowed that both ends of an edge are attached to two different marked points on the boundary. (The marked point on the boundary of the disk labelled a corresponds to the boundary edge
 $\{b_a,b_{a+1}\}$
of the cactus G. Note that we do not regard these m marked boundary points as vertices of
$\{b_a,b_{a+1}\}$
of the cactus G. Note that we do not regard these m marked boundary points as vertices of
 $G^*$
. The vertices of
$G^*$
. The vertices of
 $G^*$
are located strictly inside the disk.)
$G^*$
are located strictly inside the disk.) -
2. The vertices of
 $G^*$
are 3-valent. The vertices of
$G^*$
are 3-valent. The vertices of
 $G^*$
are colored in two colors: black and white. (The vertices of
$G^*$
are colored in two colors: black and white. (The vertices of
 $G^*$
correspond to triangles of the membrane M. They are colored according to the colors of triangles in M. Note that the m marked boundary points of the disk are not colored.)
$G^*$
correspond to triangles of the membrane M. They are colored according to the colors of triangles in M. Note that the m marked boundary points of the disk are not colored.) -
3. The faces
 $F_v$
of
$F_v$
of
 $G^*$
(associated with vertices v of G) are labelled by the vectors
$G^*$
(associated with vertices v of G) are labelled by the vectors
 $f(v)\in \mathbb {Z}^n$
. For a pair of faces
$f(v)\in \mathbb {Z}^n$
. For a pair of faces
 $F_u$
and
$F_u$
and
 $F_v$
sharing an edge, we have
$F_v$
sharing an edge, we have
 $f(u)-f(v)=e_i - e_j$
, for some
$f(u)-f(v)=e_i - e_j$
, for some
 $i\ne j$
.
$i\ne j$
.
Plane graphs
![]() $G^*$
satisfying conditions (1), (2) above are plabic graphs in the sense of [Reference PostnikovPo06, Section 11], that are additionally
$G^*$
satisfying conditions (1), (2) above are plabic graphs in the sense of [Reference PostnikovPo06, Section 11], that are additionally
![]() $3$
-valentFootnote 6.
$3$
-valentFootnote 6.
Definition 21.2. A plabic graph is the plane dual
![]() $G^*$
of a cactus G with all vertices colored in two colors: black and white (this graph may contain edges between vertices of the same color).
$G^*$
of a cactus G with all vertices colored in two colors: black and white (this graph may contain edges between vertices of the same color).
A
![]() $\mathbb {Z}^n$
-labelled plabic graph is a pair
$\mathbb {Z}^n$
-labelled plabic graph is a pair
![]() $(G^*,f)$
, where
$(G^*,f)$
, where
![]() $G^*$
is the plane dual of a cactus G, such that
$G^*$
is the plane dual of a cactus G, such that
![]() $M=(G,f)$
is a membrane. Equivalently, a
$M=(G,f)$
is a membrane. Equivalently, a
![]() $\mathbb {Z}^n$
-labelled plabic graph is a pair
$\mathbb {Z}^n$
-labelled plabic graph is a pair
![]() $(G^*,f)$
satisfying conditions (1), (2), and (3) above.
$(G^*,f)$
satisfying conditions (1), (2), and (3) above.
Clearly, by the definition, membranes
![]() $M=(G,f)$
are in bijection with
$M=(G,f)$
are in bijection with
![]() $\mathbb {Z}^n$
-labelled plabic graphs
$\mathbb {Z}^n$
-labelled plabic graphs
![]() $(G^*,f)$
.
$(G^*,f)$
.
Remark 21.3. For a membrane
![]() $M=(G,f)$
, the cactus G is indecomposable if and only if the plabic graph
$M=(G,f)$
, the cactus G is indecomposable if and only if the plabic graph
![]() $G^*$
is connected.
$G^*$
is connected.
Let us give another description of membranes and
![]() $\mathbb {Z}^n$
-labelled plabic graphs. We recall the definition of strands (or trips) in plabic graphs.
$\mathbb {Z}^n$
-labelled plabic graphs. We recall the definition of strands (or trips) in plabic graphs.
Definition 21.4 [Reference PostnikovPo06, Section 13]
For a plabic graph
![]() $G^*$
, a strand in
$G^*$
, a strand in
![]() $G^*$
is a directed walk along the edges of
$G^*$
is a directed walk along the edges of
![]() $G^*$
that satisfies the following “rules of the road”:
$G^*$
that satisfies the following “rules of the road”:
-
○ Turn right at a black vertex.
-
○ Turn left at a white vertex.
Each strand is either a walk between two marked points on the boundary of the disk, or a closed walk.
The strand permutation
![]() $\pi :[m]\to [m]$
of a plabic graph
$\pi :[m]\to [m]$
of a plabic graph
![]() $G^*$
is given by
$G^*$
is given by
![]() $\pi (s)=t$
, if the strand that starts at the marked point s on the boundary of the disk ends at the marked point t.
$\pi (s)=t$
, if the strand that starts at the marked point s on the boundary of the disk ends at the marked point t.
Let
![]() $\mathrm {Strand}(G^*)$
be the set of all strands in
$\mathrm {Strand}(G^*)$
be the set of all strands in
![]() $G^*$
. For every edge
$G^*$
. For every edge
![]() $\{a,b\}$
of
$\{a,b\}$
of
![]() $G^*$
, there are two strands in
$G^*$
, there are two strands in
![]() $\mathrm {Strand}(G^*)$
that pass through the edge: one passing in the direction
$\mathrm {Strand}(G^*)$
that pass through the edge: one passing in the direction
![]() $a\to b$
and the other passing in the direction
$a\to b$
and the other passing in the direction
![]() $b\to a$
. We call such a pair of strands an intersecting pair of strands. If these two intersecting strands happen to be the same strand, we call it a self-intersecting strand.
$b\to a$
. We call such a pair of strands an intersecting pair of strands. If these two intersecting strands happen to be the same strand, we call it a self-intersecting strand.
Theorem 21.5. Let
![]() $G^*$
be a fixed plabic graph, and let
$G^*$
be a fixed plabic graph, and let
![]() $F_0$
be a fixed reference face of
$F_0$
be a fixed reference face of
![]() $G^*$
. The set of all
$G^*$
. The set of all
![]() $\mathbb {Z}^n$
-labelled plabic graphs
$\mathbb {Z}^n$
-labelled plabic graphs
![]() $(G^*,f)$
, and thus all membranes
$(G^*,f)$
, and thus all membranes
![]() $(G,f)$
, are in bijection with the following data:
$(G,f)$
, are in bijection with the following data:
-
1. An integer vector in
 $\mathbb {Z}^n$
, which is the label of the reference face
$\mathbb {Z}^n$
, which is the label of the reference face
 $F_0$
.
$F_0$
. -
2. A map
 $g:\mathrm {Strand}(G^*)\to \{1,\dots ,n\}$
that satisfies the condition: (21.1)
$g:\mathrm {Strand}(G^*)\to \{1,\dots ,n\}$
that satisfies the condition: (21.1) $$ \begin{align} g(S)\ne g(T),\quad \textrm{for any pair of intersecting strands } S \textrm{ and } T. \end{align} $$
$$ \begin{align} g(S)\ne g(T),\quad \textrm{for any pair of intersecting strands } S \textrm{ and } T. \end{align} $$
Explicitly, the strand labelling g is obtained from the face labelling f by the following condition: if
![]() $S\in \mathrm {Strand}(G^*)$
is the strand passing through some edge
$S\in \mathrm {Strand}(G^*)$
is the strand passing through some edge
![]() $\{a,b\}$
of
$\{a,b\}$
of
![]() $G^*$
in the direction
$G^*$
in the direction
![]() $a\to b$
, and
$a\to b$
, and
![]() $F_u$
and
$F_u$
and
![]() $F_v$
are the two adjacent faces of
$F_v$
are the two adjacent faces of
![]() $G^*$
located, respectively, to the left and to the right of the edge
$G^*$
located, respectively, to the left and to the right of the edge
![]() $a\to b$
, and if
$a\to b$
, and if
![]() $f(u)-f(v)=e_i-e_j$
, then
$f(u)-f(v)=e_i-e_j$
, then
![]() $g(S) = i$
.
$g(S) = i$
.
In particular, (21.1) implies that, for any membrane
![]() $(G,f)$
, the plabic graph
$(G,f)$
, the plabic graph
![]() $G^*$
cannot have self-intersecting strands. Changing the label of the reference face
$G^*$
cannot have self-intersecting strands. Changing the label of the reference face
![]() $F_0$
accounts for affine translations of membranes in
$F_0$
accounts for affine translations of membranes in
![]() $\mathbb {R}^n$
. Up to affine translations, membranes correspond just to the strand labelling g satisfying condition (2).
$\mathbb {R}^n$
. Up to affine translations, membranes correspond just to the strand labelling g satisfying condition (2).
Proof. First, it is easy to check, using the rules of the road, that the description of the strand labelling g in terms of face labelling f is locally consistent, that is, for any vertex of
![]() $G^*$
, the label of some strand passing through this vertex obtained using its incoming edge to the vertex coincides with the label obtained using its outgoing edge. This implies the global consistence of the strand labelling g: For any strand S, the label
$G^*$
, the label of some strand passing through this vertex obtained using its incoming edge to the vertex coincides with the label obtained using its outgoing edge. This implies the global consistence of the strand labelling g: For any strand S, the label
![]() $g(S)$
obtained using any edge of S does not depend on a choice of the edge.
$g(S)$
obtained using any edge of S does not depend on a choice of the edge.
Condition (2) for the strand labelling g follows from the fact, that, for a pair of strands S and T intersecting at an edge of
![]() $G^*$
with two faces
$G^*$
with two faces
![]() $F_u$
and
$F_u$
and
![]() $F_v$
adjacent to the edge, we have
$F_v$
adjacent to the edge, we have
![]() $g(S)=i$
and
$g(S)=i$
and
![]() $g(T)=j$
, where
$g(T)=j$
, where
![]() $f(u)-f(v)=e_i-e_j\ne 0$
.
$f(u)-f(v)=e_i-e_j\ne 0$
.
Conversely, let
![]() $v_0$
be the vertex of the cactus G corresponding to the reference face
$v_0$
be the vertex of the cactus G corresponding to the reference face
![]() $F_0$
of
$F_0$
of
![]() $G^*$
. Let
$G^*$
. Let
![]() $f(v_0)\in \mathbb {Z}^n$
be any integer vector, and let g be any strand labelling satisfying condition (2). For any vertex v of the cactus G, we can construct the vector
$f(v_0)\in \mathbb {Z}^n$
be any integer vector, and let g be any strand labelling satisfying condition (2). For any vertex v of the cactus G, we can construct the vector
![]() $f(v)\in \mathbb {Z}^n$
by picking a path P in G from
$f(v)\in \mathbb {Z}^n$
by picking a path P in G from
![]() $v_0$
to v and using the relationship between f and g, for all edges of the path P. The rules of the road imply that the label
$v_0$
to v and using the relationship between f and g, for all edges of the path P. The rules of the road imply that the label
![]() $f(v)$
does not change if we locally modify the path P along a (triangular) face of the cactus G. This implies the independence of this construction for
$f(v)$
does not change if we locally modify the path P along a (triangular) face of the cactus G. This implies the independence of this construction for
![]() $f(v)$
from a choice of path P. Clearly, this function f, constructed from
$f(v)$
from a choice of path P. Clearly, this function f, constructed from
![]() $f(v_0)$
and g, gives a valid membrane
$f(v_0)$
and g, gives a valid membrane
![]() $(G,f)$
.
$(G,f)$
.
By Theorem 21.5, the strands of a
![]() $\mathbb {Z}^n$
-labeled plabic graph are not self-intersecting.
$\mathbb {Z}^n$
-labeled plabic graph are not self-intersecting.
Corollary 21.6. The strand permutation
![]() $\pi $
of a
$\pi $
of a
![]() $\mathbb {Z}^n$
-labeled plabic graph is a derangement, that is, a permutation in
$\mathbb {Z}^n$
-labeled plabic graph is a derangement, that is, a permutation in
![]() $S_m$
, such that
$S_m$
, such that
![]() $\pi (s)\ne s$
for any
$\pi (s)\ne s$
for any
![]() $s\in [m]$
.
$s\in [m]$
.
In [Reference PostnikovPo06], strand permutations were decorated permutations with two types of fixed points (see Section 2). Here, we do not allow plabic graphs to have boundary leaves, so their strand permutations do not have fixed points.
22. Moves of plabic graphs and membranes
In [Reference PostnikovPo06, Section 12], the three types of local moves of plabic graphs were defined, which are shown below on Figure 3.

Figure 3 Moves of plabic graphs: (I) contraction-uncontraction of black vertices, (II) square move, and (III) contraction-uncontraction of white vertices.
It is easy to see from the rules of the road that we have:
Lemma 22.1 [Reference PostnikovPo06, Lemma 13.1]
Any two plabic graphs connected with each other by a sequence of local moves of types (I), (II), or (III) have the same strand permutations.
The local moves of plabic graphs can be converted into local moves of membranes, as follows.
Lemma 22.2. Let
![]() $M=(G,f)$
be a membrane. Let
$M=(G,f)$
be a membrane. Let
![]() $F_u$
be a square face of
$F_u$
be a square face of
![]() $G^*$
with vertices of alternating colors as we go around
$G^*$
with vertices of alternating colors as we go around
![]() $F_u$
, that is, a face of
$F_u$
, that is, a face of
![]() $G^*$
on which one can perform a square move (II). Let
$G^*$
on which one can perform a square move (II). Let
![]() $F_v, F_w, F_z, F_t$
be the four adjacent faces of
$F_v, F_w, F_z, F_t$
be the four adjacent faces of
![]() $G^*$
in the clockwise order. Then
$G^*$
in the clockwise order. Then
![]() $\mathrm {conv}(f(u), f(v), f(w), f(z), f(t))$
is a square pyramid in
$\mathrm {conv}(f(u), f(v), f(w), f(z), f(t))$
is a square pyramid in
![]() $\mathbb {R}^n$
, such that
$\mathbb {R}^n$
, such that
-
○ The pyramid has one square face (the base) and four faces given by equilateral triangles. All edges of the pyramid have equal lengths.
-
○
 $f(u)$
is the apex of the pyramid.
$f(u)$
is the apex of the pyramid. -
○ The base is the square,
 $\mathrm {conv}(f(v), f(w), f(z), f(t))$
with vertices arranged as we go around the base.
$\mathrm {conv}(f(v), f(w), f(z), f(t))$
with vertices arranged as we go around the base.
For a pyramid, as in the lemma above, let
![]() $\widetilde {f(u)}\in \mathbb {R}^n$
be the reflection of
$\widetilde {f(u)}\in \mathbb {R}^n$
be the reflection of
![]() $f(u)$
with respect to the affine plane containing the points
$f(u)$
with respect to the affine plane containing the points
![]() $f(v), f(w), f(z), f(t)$
, that is, it is given by
$f(v), f(w), f(z), f(t)$
, that is, it is given by
Clearly,
![]() $\mathrm {conv}(\widetilde {f(u)}, f(u), f(v), f(w), f(z),f(t))$
is an octahedron, which is the union of two square pyramids. The following lemma follows from the definitions.
$\mathrm {conv}(\widetilde {f(u)}, f(u), f(v), f(w), f(z),f(t))$
is an octahedron, which is the union of two square pyramids. The following lemma follows from the definitions.
Lemma 22.3. Let
![]() $M=(G,f)$
be a membrane, and let
$M=(G,f)$
be a membrane, and let
![]() $G^*\to \tilde G^*$
be any local move of the plabic graph
$G^*\to \tilde G^*$
be any local move of the plabic graph
![]() $G^*$
of type (I), (II), or (III). Let
$G^*$
of type (I), (II), or (III). Let
![]() $\tilde G$
be the plane dual of the plabic graph
$\tilde G$
be the plane dual of the plabic graph
![]() $\tilde G^*$
. The vertex set
$\tilde G^*$
. The vertex set
![]() $\tilde {\mathrm {Vert}}$
of
$\tilde {\mathrm {Vert}}$
of
![]() $\tilde G$
can be naturally identified with the vertex set
$\tilde G$
can be naturally identified with the vertex set
![]() ${\mathrm {Vert}}$
of G. Let
${\mathrm {Vert}}$
of G. Let
![]() $\tilde f:\tilde {\mathrm {Vert}} \to \mathbb {Z}^n$
be the map defined, as follows.
$\tilde f:\tilde {\mathrm {Vert}} \to \mathbb {Z}^n$
be the map defined, as follows.
-
○ For a move of type (I) or (III), assume that
(22.2)where $$ \begin{align} f(u)\ne f(w), \end{align} $$
$$ \begin{align} f(u)\ne f(w), \end{align} $$
 $F_u$
and
$F_u$
and
 $F_w$
are two of the four faces
$F_w$
are two of the four faces
 $F_u,F_v,F_w,F_z$
of
$F_u,F_v,F_w,F_z$
of
 $G^*$
involved in the move, which are not adjacent faces of
$G^*$
involved in the move, which are not adjacent faces of
 $G^*$
. Then define
$G^*$
. Then define
 $\tilde f := f$
.
$\tilde f := f$
.
-
○ For a square move (II), let
 $F_u,F_v,F_w,F_z,F_t$
be the faces of
$F_u,F_v,F_w,F_z,F_t$
be the faces of
 $G^*$
involved in the move, labelled as in Lemma 22.2, then set
$G^*$
involved in the move, labelled as in Lemma 22.2, then set
 $\tilde f(u) := \widetilde {f(u)}$
, given by (22.1). For all other
$\tilde f(u) := \widetilde {f(u)}$
, given by (22.1). For all other
 $x\ne u$
, set
$x\ne u$
, set
 $\tilde f(x) :=f(x)$
.
$\tilde f(x) :=f(x)$
.
Then
![]() $\tilde M := (\tilde G, \tilde f)$
is a valid membrane with the same boundary loop L as M.
$\tilde M := (\tilde G, \tilde f)$
is a valid membrane with the same boundary loop L as M.
Definition 22.4. Local moves of membranes of types (I), (II), or (III) are the moves
![]() $M\to \tilde M$
in Lemma 22.3.
$M\to \tilde M$
in Lemma 22.3.
Moves of types (I) and (III) correspond to tetrahedron moves of membranes, where we replace two triangles on the surface of a tetrahedron by the other two triangles. Moves of type (II) correspond to octahedron moves of membranes, where we replace four triangles forming a half of the surface of an octahedron by the four triangles on the other half of the surface of the octahedron, as shown in Figure 4 (see also [Reference Farber and PostnikovFP]).

Figure 4 Moves of plabic graphs (top) and membranes (bottom): tetrahedron moves (left), and octahedron move (right).
Remark 22.5. There is only one situation when there is a valid move
![]() $G^*\to \tilde G^*$
of plabic graphs, but there is no corresponding move of membranes
$G^*\to \tilde G^*$
of plabic graphs, but there is no corresponding move of membranes
![]() $M\to \tilde M$
. This happens if the move of plabic graphs is of type (I) or (III) and condition (22.2) fails. In this case, in the picture shown on the bottom left of Figure 4, the two triangles before the move coincide with each other. The move would transform them into two “degenerate triangles”, that is, line segments, which we do not allow in a membrane (recall that we require that
$M\to \tilde M$
. This happens if the move of plabic graphs is of type (I) or (III) and condition (22.2) fails. In this case, in the picture shown on the bottom left of Figure 4, the two triangles before the move coincide with each other. The move would transform them into two “degenerate triangles”, that is, line segments, which we do not allow in a membrane (recall that we require that
![]() $f(u)\ne f(v)$
for any edge
$f(u)\ne f(v)$
for any edge
![]() $\{u,v\}$
of G).
$\{u,v\}$
of G).
However, for any membrane
![]() $M=(G,f)$
and any square move (II) of the plabic graph
$M=(G,f)$
and any square move (II) of the plabic graph
![]() $G^*$
, there is always the associated valid octahedron move of the membrane M.
$G^*$
, there is always the associated valid octahedron move of the membrane M.
Remark 22.6. According to [Reference PostnikovPo18], the three types of moves of plabic graphs correspond to the three 3-dimensional hypersimplices:
![]() $\Delta _{14}$
(tetrahedron),
$\Delta _{14}$
(tetrahedron),
![]() $\Delta _{24}$
(octahedron), and
$\Delta _{24}$
(octahedron), and
![]() $\Delta _{34}$
(upside down tetrahedron). Moves of certain 3-dimensional membranes were used in [Reference Farber and PostnikovFP, Section 12.6] to graphically describe “chain reactions” on plabic graphs.
$\Delta _{34}$
(upside down tetrahedron). Moves of certain 3-dimensional membranes were used in [Reference Farber and PostnikovFP, Section 12.6] to graphically describe “chain reactions” on plabic graphs.
Clearly,
![]() $\mathrm {Area}(M)$
is preserved under the local moves of membranes, and the boundary loop L does not change. So the class of minimal membranes with a given boundary loop L is invariant under these three types of moves of membranes.
$\mathrm {Area}(M)$
is preserved under the local moves of membranes, and the boundary loop L does not change. So the class of minimal membranes with a given boundary loop L is invariant under these three types of moves of membranes.
Remark 22.7. The exceptional case when condition (22.2) fails and the move of membranes is not defined (see Remark 22.5) can never happen in a minimal membrane. Indeed, in this case, the two coinciding triangles in the picture on the bottom left of Figure 4 can be removed from the membrane M, so that we get a membrane with a smaller area but with the same boundary loop L.
23. Minimal membranes and reduced plabic graphs
We recall the notion of reducedness for plabic graphs. The following definition is equivalent to [Reference PostnikovPo06, Definition 12.5] by [Reference PostnikovPo06, Theorem 13.2].
Definition 23.1. A plabic graph
![]() $G^*$
is reduced if it satisfies the conditions:
$G^*$
is reduced if it satisfies the conditions:
-
1.
 $G^*$
has no self-intersecting strands.
$G^*$
has no self-intersecting strands. -
2.
 $G^*$
has no closed strands.
$G^*$
has no closed strands. -
3.
 $G^*$
has no pair of strands
$G^*$
has no pair of strands
 $S,T$
with a bad double crossing, which means, that S and T intersect at two edges
$S,T$
with a bad double crossing, which means, that S and T intersect at two edges
 $\{a,b\}$
and
$\{a,b\}$
and
 $\{c,d\}$
and both strands are directed from
$\{c,d\}$
and both strands are directed from
 $\{a,b\}$
to
$\{a,b\}$
to
 $\{c,d\}$
.
$\{c,d\}$
.
Theorem 23.2 [Reference PostnikovPo06, Theorem 13.4]
For any two reduced plabic graphs with the same number of marked points on the disk, the graphs have the same strand permutations if and only if they can be obtained from each other by a sequence of local moves of types (I), (II), and (III).
Let us discuss a relationship between minimal membranes and reduced plabic graphs.
Theorem 23.3. If
![]() $M=(G,f)$
is a minimal membrane, then
$M=(G,f)$
is a minimal membrane, then
![]() $G^*$
is a reduced plabic graph. Moreover, for a minimal membrane
$G^*$
is a reduced plabic graph. Moreover, for a minimal membrane
![]() $M=(G,f)$
with boundary loop
$M=(G,f)$
with boundary loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
(where
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
(where
![]() $\lambda ^{(a+1)}-\lambda ^{(a)} = e_{i_a}-e_{j_a}$
, for
$\lambda ^{(a+1)}-\lambda ^{(a)} = e_{i_a}-e_{j_a}$
, for
![]() $a\in \mathbb {Z}/m\mathbb {Z}$
), one can recover the strand labelling g (and thus the face labelling f) from the plabic graph
$a\in \mathbb {Z}/m\mathbb {Z}$
), one can recover the strand labelling g (and thus the face labelling f) from the plabic graph
![]() $G^*$
and loop L as follows: If
$G^*$
and loop L as follows: If
![]() $S\in \mathrm {Strand}(G^*)$
is a strand in
$S\in \mathrm {Strand}(G^*)$
is a strand in
![]() $G^*$
connecting two marked points labelled s (the source of S) and t (the target of S) on the boundary of the disk, then we have
$G^*$
connecting two marked points labelled s (the source of S) and t (the target of S) on the boundary of the disk, then we have
Proof. Suppose that
![]() $M=(G,f)$
is a minimal membrane, but
$M=(G,f)$
is a minimal membrane, but
![]() $G^*$
is not a reduced plabic graph. According to [Reference PostnikovPo06, Sections 12, 13], one can apply a sequence of moves (I), (II), and (III) to
$G^*$
is not a reduced plabic graph. According to [Reference PostnikovPo06, Sections 12, 13], one can apply a sequence of moves (I), (II), and (III) to
![]() $G^*$
and obtain a plabic graph with a double edge. By Remark 22.7, if
$G^*$
and obtain a plabic graph with a double edge. By Remark 22.7, if
![]() $M=(G,f)$
is a minimal membrane, then, for any sequence of local moves of plabic graphs starting with
$M=(G,f)$
is a minimal membrane, then, for any sequence of local moves of plabic graphs starting with
![]() $G^*$
, there is an associated sequence of local moves of membranes. So we get some minimal membrane whose plabic graph has a double edge. However, we have:
$G^*$
, there is an associated sequence of local moves of membranes. So we get some minimal membrane whose plabic graph has a double edge. However, we have:
-
1. There is no membrane (minimal or not) whose plabic graph has a double edge with vertices of different colors. Indeed, such a plabic graph would have a self-intersecting strand, which contradicts Theorem 21.5.
-
2. If the plabic graph of a membrane has a double edge with vertices of the same color, then the membrane is not minimal, because we can remove two triangles from it (corresponding to the two vertices of the plabic graph connected by the double edge), and get a membrane of smaller area with the same boundary loop.
In both cases, we get a contradiction, which proves the first part of the theorem.
The second part follows from the fact that a reduced plabic graph
![]() $G^*$
cannot contain a closed strand. So any strand S of
$G^*$
cannot contain a closed strand. So any strand S of
![]() $G^*$
connects two marked points s (source) and t (target) on the boundary of the disk. Applying Theorem 21.5 (that relates the strand labelling g to the face labelling of f of a plabic graph) to the first and the last edges of the strand S, that is, the edges of S connected to the marked points s and t on the boundary of the disk, we get exactly the needed equality
$G^*$
connects two marked points s (source) and t (target) on the boundary of the disk. Applying Theorem 21.5 (that relates the strand labelling g to the face labelling of f of a plabic graph) to the first and the last edges of the strand S, that is, the edges of S connected to the marked points s and t on the boundary of the disk, we get exactly the needed equality
![]() $g(S)= i_s = j_t$
.
$g(S)= i_s = j_t$
.
In general, a nonminimal membrane
![]() $M=(G,f)$
can give rise to a reduced plabic graph
$M=(G,f)$
can give rise to a reduced plabic graph
![]() $G^*$
. However, for a special class of loops, minimality of M is equivalent to reducedness of
$G^*$
. However, for a special class of loops, minimality of M is equivalent to reducedness of
![]() $G^*$
.
$G^*$
.
Recall that a sequence
![]() $(c_1,\dots ,c_m)$
of real numbers is unimodal if
$(c_1,\dots ,c_m)$
of real numbers is unimodal if
![]() $c_1\leq \cdots \leq c_k \geq c_{k+1} \geq \cdots \geq c_m$
, for some
$c_1\leq \cdots \leq c_k \geq c_{k+1} \geq \cdots \geq c_m$
, for some
![]() $k\in [m]$
. Let us say that a sequence
$k\in [m]$
. Let us say that a sequence
![]() $(c_1,\dots ,c_m)$
is cyclically unimodal if it is unimodal up to a possible cyclic shift, that is, if
$(c_1,\dots ,c_m)$
is cyclically unimodal if it is unimodal up to a possible cyclic shift, that is, if
![]() $(c_r, c_{r+1}, \dots , c_m, c_1,\dots ,c_{r-1})$
is unimodal for some
$(c_r, c_{r+1}, \dots , c_m, c_1,\dots ,c_{r-1})$
is unimodal for some
![]() $r\in [m]$
.
$r\in [m]$
.
Definition 23.4. We say that a loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is unimodal if each of its coordinate sequences
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
is unimodal if each of its coordinate sequences
![]() $(\lambda ^{(1)}_i,\dots ,\lambda ^{(m)}_i)$
, for
$(\lambda ^{(1)}_i,\dots ,\lambda ^{(m)}_i)$
, for
![]() $i\in [n]$
, is a cyclically unimodal sequence.
$i\in [n]$
, is a cyclically unimodal sequence.
Equivalently, a loop L (with
![]() $\lambda ^{(a+1)}-\lambda ^{(a)}=e_{i_a}-e_{j_a}$
, for
$\lambda ^{(a+1)}-\lambda ^{(a)}=e_{i_a}-e_{j_a}$
, for
![]() $a\in \mathbb {Z}/m\mathbb {Z}$
) is unimodal if there is no
$a\in \mathbb {Z}/m\mathbb {Z}$
) is unimodal if there is no
![]() $4$
-tuple of indices
$4$
-tuple of indices
![]() $a<b<c<d$
in
$a<b<c<d$
in
![]() $[m]$
, such that
$[m]$
, such that
![]() $i_a=j_b=i_c=j_d$
or
$i_a=j_b=i_c=j_d$
or
![]() $j_a=i_b=j_c=i_d$
.
$j_a=i_b=j_c=i_d$
.
Consider a disk with m marked points on its boundary labelled
![]() $1,\dots ,m$
in the clockwise order. For
$1,\dots ,m$
in the clockwise order. For
![]() $s,t\in [m]$
, let
$s,t\in [m]$
, let
![]() $|s,t|$
denote the chord in the disk that connects two marked boundary points labelled s and t. We say that two chords
$|s,t|$
denote the chord in the disk that connects two marked boundary points labelled s and t. We say that two chords
![]() $|s,t|$
and
$|s,t|$
and
![]() $|s',t'|$
are noncrossing if they do not intersect each other in the disk.
$|s',t'|$
are noncrossing if they do not intersect each other in the disk.
Definition 23.5. For a unimodal loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
(with
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
(with
![]() $\lambda ^{(a+1)}-\lambda ^{(a)}=e_{i_a}-e_{j_a}$
for
$\lambda ^{(a+1)}-\lambda ^{(a)}=e_{i_a}-e_{j_a}$
for
![]() $a\in \mathbb {Z}/m\mathbb {Z}$
), define
$a\in \mathbb {Z}/m\mathbb {Z}$
), define
![]() $\pi =\pi _L$
as the unique permutation
$\pi =\pi _L$
as the unique permutation
![]() $\pi :[m]\to [m]$
, such that
$\pi :[m]\to [m]$
, such that
-
○ For any
 $s\in [m]$
, we have
$s\in [m]$
, we have
 $i_s=j_{\pi (s)}$
.
$i_s=j_{\pi (s)}$
. -
○ If
 $i_s = i_{s'}$
, for some
$i_s = i_{s'}$
, for some
 $s\ne s'\in [m]$
, then the two chords
$s\ne s'\in [m]$
, then the two chords
 $|s, \pi (s)|$
and
$|s, \pi (s)|$
and
 $|s',\pi (s')|$
are noncrossing.
$|s',\pi (s')|$
are noncrossing.
Explicitly, the permutation
![]() $\pi =\pi _L$
is given, as follows. For any
$\pi =\pi _L$
is given, as follows. For any
![]() $i\in [n]$
, let
$i\in [n]$
, let
![]() $s_1,\dots ,s_p$
be all indices, such that
$s_1,\dots ,s_p$
be all indices, such that
![]() $i_{s_1}=i_{s_2}=\cdots = i_{s_p}=i$
; and let
$i_{s_1}=i_{s_2}=\cdots = i_{s_p}=i$
; and let
![]() $t_1,\dots ,t_p$
be all indices, such that
$t_1,\dots ,t_p$
be all indices, such that
![]() $j_{t_1}=j_{t_2}=\cdots = j_{t_p}=i$
. Since L is unimodal, we may assume that these indices are arranged as
$j_{t_1}=j_{t_2}=\cdots = j_{t_p}=i$
. Since L is unimodal, we may assume that these indices are arranged as
![]() $s_1<s_2<\cdots <s_p< t_1<t_2<\cdots <t_p$
(up to a cyclic shift). Then we have
$s_1<s_2<\cdots <s_p< t_1<t_2<\cdots <t_p$
(up to a cyclic shift). Then we have
![]() $\pi (s_1)=t_p$
,
$\pi (s_1)=t_p$
,
![]() $\pi (s_2)=t_{p-1}$
, …,
$\pi (s_2)=t_{p-1}$
, …,
![]() $\pi (s_p)=t_1$
.
$\pi (s_p)=t_1$
.
Theorem 23.6. Fix a unimodal loop L. The map
![]() $M=(G,f)\mapsto G^*$
gives a bijection between the following two sets:
$M=(G,f)\mapsto G^*$
gives a bijection between the following two sets:
-
○ The set of minimal membranes M with boundary loop L.
-
○ The set of reduced plabic graphs
 $G^*$
with strand permutation
$G^*$
with strand permutation
 $\pi _L$
.
$\pi _L$
.
All minimal membranes with boundary loop L are connected by local moves of membranes of types (I), (II), and (III).
Proof. Let
![]() $M=(G,f)$
be a minimal membrane with boundary loop L. According to Theorem 21.5, two strands S and T of
$M=(G,f)$
be a minimal membrane with boundary loop L. According to Theorem 21.5, two strands S and T of
![]() $G^*$
that have the same strand label
$G^*$
that have the same strand label
![]() $g(S)=g(T)$
cannot intersect each other. For
$g(S)=g(T)$
cannot intersect each other. For
![]() $i\in [n]$
, let
$i\in [n]$
, let
![]() $s_1,\dots ,s_p, t_1,\dots ,t_p$
be sequence of sources and targets as in Definition 23.5. These sources should be connected with the targets by strands
$s_1,\dots ,s_p, t_1,\dots ,t_p$
be sequence of sources and targets as in Definition 23.5. These sources should be connected with the targets by strands
![]() $S_1,\dots ,S_p$
that all have the same label
$S_1,\dots ,S_p$
that all have the same label
![]() $g(S_1)=\dots =g(S_p)=i$
. Since the sources and the targets are separated from each other on the boundary of the disk, there exists a unique matching between them, given by a collection of pairwise noncrossing strands. Namely, the strand
$g(S_1)=\dots =g(S_p)=i$
. Since the sources and the targets are separated from each other on the boundary of the disk, there exists a unique matching between them, given by a collection of pairwise noncrossing strands. Namely, the strand
![]() $S_a$
starting at the source
$S_a$
starting at the source
![]() $s_a$
should end at the target
$s_a$
should end at the target
![]() $t_{p+1-a}$
, for
$t_{p+1-a}$
, for
![]() $a=1,\dots ,p$
. Thus, the strand permutation of
$a=1,\dots ,p$
. Thus, the strand permutation of
![]() $G^*$
is exactly the permutation
$G^*$
is exactly the permutation
![]() $\pi _L$
given by Definition 23.5. Since we know that all reduced plabic graphs with the same strand permutation are connected with each other by the local moves, and there are corresponding local moves of membranes, we deduce all the claims of the theorem.
$\pi _L$
given by Definition 23.5. Since we know that all reduced plabic graphs with the same strand permutation are connected with each other by the local moves, and there are corresponding local moves of membranes, we deduce all the claims of the theorem.
Let us give explicit expressions for the surface area and the number of lattice points of a minimal membrane using the results of [Reference PostnikovPo06].
Definition 23.7 [Reference PostnikovPo06, Section 17]
Let
![]() $\pi :[m]\to [m]$
be a derangement, that is, a permutation, such that
$\pi :[m]\to [m]$
be a derangement, that is, a permutation, such that
![]() $\pi (a)\ne a$
, for any a. Define:
$\pi (a)\ne a$
, for any a. Define:
-
○ The number of antiexceedances in
 $\pi $
$\pi $
 $$ \begin{align*}k(\pi) := \#\{a\in[m]\mid \pi(a)<a\}. \end{align*} $$
$$ \begin{align*}k(\pi) := \#\{a\in[m]\mid \pi(a)<a\}. \end{align*} $$
-
○ The number of alignments in
 $\pi $
$\pi $
 $$ \begin{align*}A(\pi) := \left\{(a,b)\in[m]^2\mid \begin{array}{l} a<b<\pi(b) <\pi(a), \textrm{ or } \pi(a)<a<b<\pi(b), \textrm{ or } \\ \pi(b) <\pi(a) < a < b,\textrm{ or } b<\pi(b) <\pi(a) < a \end{array}\!\right\} .\end{align*} $$
$$ \begin{align*}A(\pi) := \left\{(a,b)\in[m]^2\mid \begin{array}{l} a<b<\pi(b) <\pi(a), \textrm{ or } \pi(a)<a<b<\pi(b), \textrm{ or } \\ \pi(b) <\pi(a) < a < b,\textrm{ or } b<\pi(b) <\pi(a) < a \end{array}\!\right\} .\end{align*} $$
Recall that the surface area
![]() $\mathrm {Area}(M)$
of a membrane
$\mathrm {Area}(M)$
of a membrane
![]() $M=(G,f)$
is the number of faces (triangles)
$M=(G,f)$
is the number of faces (triangles)
![]() $\Delta $
of the cactus G, or, equivalently, the number of vertices of the plabic graph
$\Delta $
of the cactus G, or, equivalently, the number of vertices of the plabic graph
![]() $G^*$
. Also denote the number of lattice points of M by
$G^*$
. Also denote the number of lattice points of M by
Proposition 23.8 (cf. [Reference PostnikovPo06, Proposition 17.10])
Let L be a unimodal loop, and let
![]() $\pi =\pi _L:[m]\to [m]$
be the associated permutation (see Definition 23.5). The number of lattice points and the surface area of a minimal membrane M with boundary loop L are equal to
$\pi =\pi _L:[m]\to [m]$
be the associated permutation (see Definition 23.5). The number of lattice points and the surface area of a minimal membrane M with boundary loop L are equal to
 $$ \begin{align*}\begin{array}{l} \mathrm{LatticePoints}(M) = k(\pi)(m-k(\pi))-A(\pi) + 1,\\[.05in] \mathrm{Area}(M) = 2\left(k(\pi)(m-k(\pi))-A(\pi)\right) - m. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l} \mathrm{LatticePoints}(M) = k(\pi)(m-k(\pi))-A(\pi) + 1,\\[.05in] \mathrm{Area}(M) = 2\left(k(\pi)(m-k(\pi))-A(\pi)\right) - m. \end{array} \end{align*} $$
Proof. For a membrane
![]() $M=(G,f)$
, the number
$M=(G,f)$
, the number
![]() $\mathrm {LatticePoints}(M)$
equals the number of faces of the plabic graph
$\mathrm {LatticePoints}(M)$
equals the number of faces of the plabic graph
![]() $G^*$
. The needed expression for the number of faces of a reduced plabic graph was given in [Reference PostnikovPo06, Proposition 17.10].
$G^*$
. The needed expression for the number of faces of a reduced plabic graph was given in [Reference PostnikovPo06, Proposition 17.10].
![]() $\mathrm {Area}(M)$
equals the number of vertices of the plabic graph
$\mathrm {Area}(M)$
equals the number of vertices of the plabic graph
![]() $G^*$
. Using Euler’s formula together with the fact that
$G^*$
. Using Euler’s formula together with the fact that
![]() $G^*$
is a 3-valent graph, we deduce
$G^*$
is a 3-valent graph, we deduce
which gives the stated expression for
![]() $\mathrm {Area}(M)$
.
$\mathrm {Area}(M)$
.
In the following sections, we will discuss several special classes of unimodal loops and membranes that have special properties:
 $$ \begin{align*}\left\{ \begin{array}{c}\textrm{positroid}\\ \textrm{loops}\end{array} \right\} \subset \left\{ \begin{array}{c}\textrm{polypositroid}\\ \textrm{loops}\end{array} \right\} \subset \left\{ \begin{array}{c}j\textrm{-increasing}\\ \textrm{loops}\end{array} \right\} \subset \left\{ \begin{array}{c}\textrm{unimodal}\\ \textrm{loops}\end{array} \right\}. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{c}\textrm{positroid}\\ \textrm{loops}\end{array} \right\} \subset \left\{ \begin{array}{c}\textrm{polypositroid}\\ \textrm{loops}\end{array} \right\} \subset \left\{ \begin{array}{c}j\textrm{-increasing}\\ \textrm{loops}\end{array} \right\} \subset \left\{ \begin{array}{c}\textrm{unimodal}\\ \textrm{loops}\end{array} \right\}. \end{align*} $$
They are described in terms of the associated sequences of roots
![]() $e_{i_1}-e_{j_1},\dots ,e_{i_m}-e_{j_m}\in \mathbb {Z}^n$
, by the following conditions:
$e_{i_1}-e_{j_1},\dots ,e_{i_m}-e_{j_m}\in \mathbb {Z}^n$
, by the following conditions:
-
○ Positroid loops:
 $m=n$
;
$m=n$
;
 $i_1,\dots ,i_n$
is a permutation of
$i_1,\dots ,i_n$
is a permutation of
 $1,\dots ,n$
; and
$1,\dots ,n$
; and
 $j_a=a$
, for
$j_a=a$
, for
 $a=1,\dots ,n$
.
$a=1,\dots ,n$
. -
○ Polypositroid loops:
 $j_1\leq \cdots \leq j_m$
; and if
$j_1\leq \cdots \leq j_m$
; and if
 $j_a=j_{a+1}$
, then
$j_a=j_{a+1}$
, then
 $i_{a+1} \in \{i_a-1, i_a - 2 ,\dots , j_a + 1\}$
(a cyclic interval in
$i_{a+1} \in \{i_a-1, i_a - 2 ,\dots , j_a + 1\}$
(a cyclic interval in
 $[n]$
).
$[n]$
). -
○ j-increasing loops:
 $j_1\leq \cdots \leq j_m$
.
$j_1\leq \cdots \leq j_m$
.
For example, we’ll see that positroid loops (considered up to affine translations) are in bijection with positroids, and polypositroid loops are in bijection with integer polypositroids.
24. Positroid membranes
We now discuss the distinguished class of loops and membranes related to positroids. Assume (in the notations of Section 21), that L is a loop, such that
![]() $m=n$
and
$m=n$
and
![]() $\{i_1,\dots ,i_n\}=\{j_1,\dots ,j_n\}=[n]$
are usual sets. Moreover, by permuting the coordinates in
$\{i_1,\dots ,i_n\}=\{j_1,\dots ,j_n\}=[n]$
are usual sets. Moreover, by permuting the coordinates in
![]() $\mathbb {R}^n$
, we assume that
$\mathbb {R}^n$
, we assume that
![]() $j_a = a$
, for
$j_a = a$
, for
![]() $a=1,\dots ,n$
. Such loops L (up to affine translations) correspond to Grassmann necklaces associated with positroids.
$a=1,\dots ,n$
. Such loops L (up to affine translations) correspond to Grassmann necklaces associated with positroids.
Let
![]() ${\mathcal {M}}\subset {[n]\choose k}$
be a positroid and
${\mathcal {M}}\subset {[n]\choose k}$
be a positroid and
![]() ${\mathcal {I}}=(I_1,\dots ,I_n)$
be the associated Grassmann necklace (see Section 2). To simplify the presentation, we shall assume that
${\mathcal {I}}=(I_1,\dots ,I_n)$
be the associated Grassmann necklace (see Section 2). To simplify the presentation, we shall assume that
![]() ${\mathcal {M}}$
has no loops or coloops, and thus,
${\mathcal {M}}$
has no loops or coloops, and thus,
![]() $I_{a+1}\ne I_a$
for any a. We have
$I_{a+1}\ne I_a$
for any a. We have
![]() $I_{a+1} = (I_a \setminus \{a\})\cup \{i_a\}$
, for
$I_{a+1} = (I_a \setminus \{a\})\cup \{i_a\}$
, for
![]() $a\in \mathbb {Z}/n\mathbb {Z}$
, where
$a\in \mathbb {Z}/n\mathbb {Z}$
, where
![]() $\pi =\pi _{\mathcal {M}}:a\to i_a$
is a certain permutation (derangement) of size n.
$\pi =\pi _{\mathcal {M}}:a\to i_a$
is a certain permutation (derangement) of size n.
Consider the loop
![]() $L=L_{\mathcal {M}}:=(e_{I_1},\dots ,e_{I_n})$
(recall that
$L=L_{\mathcal {M}}:=(e_{I_1},\dots ,e_{I_n})$
(recall that
![]() $e_I:=\sum _{i\in I} e_i$
). It corresponds to the sequence of roots
$e_I:=\sum _{i\in I} e_i$
). It corresponds to the sequence of roots
![]() $e_{i_1} - e_1, \dots , e_{i_n}-e_n$
.
$e_{i_1} - e_1, \dots , e_{i_n}-e_n$
.
Theorem 24.1. Minimal membranes M with boundary loop
![]() $L_{\mathcal {M}}$
are in bijection with reduced plabic graphs with strand permutations
$L_{\mathcal {M}}$
are in bijection with reduced plabic graphs with strand permutations
![]() $\pi _{\mathcal {M}}$
. The bijection is given by
$\pi _{\mathcal {M}}$
. The bijection is given by
![]() $M=(G,f)\mapsto G^*$
.
$M=(G,f)\mapsto G^*$
.
Moreover, for any such minimal membrane M, its embedding
![]() $\left <M\right>\subset \mathbb {R}^n$
is contained in the positroid polytope
$\left <M\right>\subset \mathbb {R}^n$
is contained in the positroid polytope
![]() $P_{\mathcal {M}}:=\mathrm {conv}(e_I\mid I\in {\mathcal {M}})$
.
$P_{\mathcal {M}}:=\mathrm {conv}(e_I\mid I\in {\mathcal {M}})$
.
Proof. Clearly, the loop
![]() $L_{\mathcal {M}}$
is unimodal. The first part of the above theorem follows from Theorem 23.6.
$L_{\mathcal {M}}$
is unimodal. The first part of the above theorem follows from Theorem 23.6.
For such a minimal positroid membrane
![]() $M=(G,f)$
, the vectors
$M=(G,f)$
, the vectors
![]() $f(v)\in \mathbb {Z}^n$
are related to the face labels
$f(v)\in \mathbb {Z}^n$
are related to the face labels
![]() $I(F)\in {[n]\choose k}$
of the corresponding plabic graph
$I(F)\in {[n]\choose k}$
of the corresponding plabic graph
![]() $G^*$
, which were studied in [Reference Oh, Postnikov and SpeyerOPS], as follows:
$G^*$
, which were studied in [Reference Oh, Postnikov and SpeyerOPS], as follows:
![]() $f(v) = e_{I(F_{v})}$
, for any face
$f(v) = e_{I(F_{v})}$
, for any face
![]() $F_v$
of
$F_v$
of
![]() $G^*$
. Indeed, in the case of positroid membranes, the relationship between f and the strand labelling g (given in Theorem 21.5) specializes to the definition of face labels of reduced plabic graphs.
$G^*$
. Indeed, in the case of positroid membranes, the relationship between f and the strand labelling g (given in Theorem 21.5) specializes to the definition of face labels of reduced plabic graphs.
The second claim of the above theorem now follows from the result proved in [Reference Oh, Postnikov and SpeyerOPS] that any face label
![]() $I(F)$
of a reduced plabic graph
$I(F)$
of a reduced plabic graph
![]() $G^*$
associated with a positroid
$G^*$
associated with a positroid
![]() ${\mathcal {M}}$
belongs to the positroid:
${\mathcal {M}}$
belongs to the positroid:
![]() $I(F)\in {\mathcal {M}}$
.
$I(F)\in {\mathcal {M}}$
.
25. Polypositroid membranes
We now discuss the class of loops and membranes related to integer polypositroids, which includes positroid loops and membranes from Section 24. Recall that in Section 6, we gave bijections between polypositroids
![]() $P\subset \mathbb {R}^n$
, Coxeter necklaces
$P\subset \mathbb {R}^n$
, Coxeter necklaces
![]() $\mathbf {v}=(v^{(1)},\dots ,v^{(n)})$
, and balanced digraphs. If P is an integer polypositroid, then the
$\mathbf {v}=(v^{(1)},\dots ,v^{(n)})$
, and balanced digraphs. If P is an integer polypositroid, then the
![]() $v^{(i)}$
are integer vectors, and the edge weights
$v^{(i)}$
are integer vectors, and the edge weights
![]() $m_{ij}$
of the balanced digraph are nonnegative integers.
$m_{ij}$
of the balanced digraph are nonnegative integers.
Define the perimeter
Footnote 7 of a membrane M with boundary loop
![]() $L = (\lambda ^{(1)},\dots ,\lambda ^{(m)})$
by
$L = (\lambda ^{(1)},\dots ,\lambda ^{(m)})$
by
![]() $\mathrm {Perim}\, M = m$
.
$\mathrm {Perim}\, M = m$
.
Definition 25.1. Let
![]() $P\subset \mathbb {R}^n$
be an integer polypositroid, and let
$P\subset \mathbb {R}^n$
be an integer polypositroid, and let
![]() $\mathbf {v}=(v^{(1)},\dots ,v^{(n)})$
be its Coxeter necklace. We say that a membrane M is a minimal P-membrane if
$\mathbf {v}=(v^{(1)},\dots ,v^{(n)})$
be its Coxeter necklace. We say that a membrane M is a minimal P-membrane if
-
1. The boundary loop
 $L = (\lambda ^{(1)},\dots ,\lambda ^{(m)})$
of M contains the points
$L = (\lambda ^{(1)},\dots ,\lambda ^{(m)})$
of M contains the points
 $v^{(1)}$
, …,
$v^{(1)}$
, …,
 $v^{(n)}$
in this particular cyclic order.
$v^{(n)}$
in this particular cyclic order. -
2. The membrane M has minimal possible perimeter
 $\mathrm {Perim}\,M$
among all membranes satisfying condition (1).
$\mathrm {Perim}\,M$
among all membranes satisfying condition (1). -
3. The membrane M has minimal possible surface area
 $\mathrm {Area}\,M$
among all membranes satisfying conditions (1) and (2).
$\mathrm {Area}\,M$
among all membranes satisfying conditions (1) and (2).
Remark 25.2. In the above definition, it is important to first minimize the perimeter of M, and only after that minimize the surface area. If we skip condition (2), we can always find a membrane M satisfying (1), whose surface area
![]() $\mathrm {Area}\,M$
equals zero.
$\mathrm {Area}\,M$
equals zero.
Define the standard root order as the total order
![]() $<$
on all roots
$<$
on all roots
![]() $e_i-e_j$
,
$e_i-e_j$
,
![]() $i,j\in [n]$
,
$i,j\in [n]$
,
![]() $i\ne j$
:
$i\ne j$
:
 $$ \begin{align} \begin{array}{l} (e_n-e_{1}) < (e_{n-1}-e_1)<(e_{n-2}-e_1)< \cdots < (e_2 - e_1) < \\ <(e_{1}-e_{2}) < (e_{n}-e_2)<(e_{n-1}-e_2)<\cdots < (e_3 - e_2) < \\ <(e_{2}-e_{3})< (e_{1}-e_3) < (e_{n}-e_3)<\cdots < (e_4 - e_3) < \\ \qquad \qquad \qquad \qquad \cdots \cdots \cdots \cdots \\ <(e_{n-1}-e_n)< (e_{n-2}-e_n) < (e_{n-3}-e_n)< \cdots < (e_1-e_n). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{l} (e_n-e_{1}) < (e_{n-1}-e_1)<(e_{n-2}-e_1)< \cdots < (e_2 - e_1) < \\ <(e_{1}-e_{2}) < (e_{n}-e_2)<(e_{n-1}-e_2)<\cdots < (e_3 - e_2) < \\ <(e_{2}-e_{3})< (e_{1}-e_3) < (e_{n}-e_3)<\cdots < (e_4 - e_3) < \\ \qquad \qquad \qquad \qquad \cdots \cdots \cdots \cdots \\ <(e_{n-1}-e_n)< (e_{n-2}-e_n) < (e_{n-3}-e_n)< \cdots < (e_1-e_n). \end{array} \end{align} $$
In other words, we have
![]() $e_i-e_j < e_{i'}-e_{j'}$
whenever
$e_i-e_j < e_{i'}-e_{j'}$
whenever
![]() $j<j'$
, or (
$j<j'$
, or (
![]() $j=j'$
and
$j=j'$
and
![]() $i'\in \{i-1,i-2,\dots , j+1\}$
), where elements of the interval are considered modulo n.
$i'\in \{i-1,i-2,\dots , j+1\}$
), where elements of the interval are considered modulo n.
Remark 25.3. The total order (25.1) differs from the one in Example 10.8: instead, it arises from the simple system
![]() $\{e_n-e_1, e_{n-1}-e_n, \ldots , e_2-e_3\}$
and Coxeter element
$\{e_n-e_1, e_{n-1}-e_n, \ldots , e_2-e_3\}$
and Coxeter element
![]() $ c= s_0 s_{n-1} s_{n-2} \cdots s_2$
, where
$ c= s_0 s_{n-1} s_{n-2} \cdots s_2$
, where
![]() $s_0:=(1n)$
is the reflection associated to the root
$s_0:=(1n)$
is the reflection associated to the root
![]() $e_n-e_1$
.
$e_n-e_1$
.
Definition 25.4. A polypositroid loop is a loop
![]() $L = (\lambda ^{(1)},\dots ,\lambda ^{(m)})$
, with
$L = (\lambda ^{(1)},\dots ,\lambda ^{(m)})$
, with
![]() $\lambda ^{(a)}\in \mathbb {Z}^n$
, such that
$\lambda ^{(a)}\in \mathbb {Z}^n$
, such that
![]() $\lambda ^{(a+1)}-\lambda ^{(a)}$
,
$\lambda ^{(a+1)}-\lambda ^{(a)}$
,
![]() $a=1,\dots ,m$
, is a weakly increasing sequence of roots in the standard root order.
$a=1,\dots ,m$
, is a weakly increasing sequence of roots in the standard root order.
The following two lemmas easily follow from the definitions.
Lemma 25.5. Any polypositroid loop is unimodal.
Let
![]() $P\subset \mathbb {R}^n$
be an integer polypositroid with Coxeter necklace
$P\subset \mathbb {R}^n$
be an integer polypositroid with Coxeter necklace
![]() $\mathbf {v}=(v^{(1)},\dots ,v^{(n)})$
, and let
$\mathbf {v}=(v^{(1)},\dots ,v^{(n)})$
, and let
![]() $m_{ij}$
be the edge multiplicities of the associated balanced digraph. Define the loop
$m_{ij}$
be the edge multiplicities of the associated balanced digraph. Define the loop
![]() $L_P=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
, such that
$L_P=(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
, such that
![]() $\lambda ^{(1)} = v^{(1)}$
, and the sequence of roots
$\lambda ^{(1)} = v^{(1)}$
, and the sequence of roots
![]() $\lambda ^{(a+1)}-\lambda ^{(a)}$
,
$\lambda ^{(a+1)}-\lambda ^{(a)}$
,
![]() $a=1,\dots ,m$
, is the weakly increasing sequence of roots (in the standard root order), such that each root
$a=1,\dots ,m$
, is the weakly increasing sequence of roots (in the standard root order), such that each root
![]() $e_j - e_i$
is repeated
$e_j - e_i$
is repeated
![]() $m_{ij}$
times. Note that m equals the total number of edges of the balanced bigraph.
$m_{ij}$
times. Note that m equals the total number of edges of the balanced bigraph.
Lemma 25.6.
(1) The map
![]() $P\to L_P$
is a bijection between integer polypositroids
$P\to L_P$
is a bijection between integer polypositroids
![]() $P\subset \mathbb {R}^n$
and polypositroid loops in
$P\subset \mathbb {R}^n$
and polypositroid loops in
![]() $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
(2) The Coxeter necklace
![]() $\mathbf {v}$
is a subsequence of the associated polypositroid loop
$\mathbf {v}$
is a subsequence of the associated polypositroid loop
![]() $L_P$
. Explictly,
$L_P$
. Explictly,
![]() $v^{(i+1)}=\lambda ^{(1+d_1+d_2+\cdots + d_i)}$
, for
$v^{(i+1)}=\lambda ^{(1+d_1+d_2+\cdots + d_i)}$
, for
![]() $i=0,\dots ,n$
; here,
$i=0,\dots ,n$
; here,
![]() $d_i=-(v^{(i+1)}-v^{(i)})_i =\sum _{j \neq i} m_{ij}$
, is the outdegree (or the indegree) of vertex i of the associated balanced digraph.
$d_i=-(v^{(i+1)}-v^{(i)})_i =\sum _{j \neq i} m_{ij}$
, is the outdegree (or the indegree) of vertex i of the associated balanced digraph.
Recall that, for a unimodal loop L, we defined the permutation
![]() $\pi _L:[m]\to [m]$
(see Definition 23.5).
$\pi _L:[m]\to [m]$
(see Definition 23.5).
Theorem 25.7. Let
![]() $P\subset \mathbb {R}^n$
be an integer polypositroid, and let
$P\subset \mathbb {R}^n$
be an integer polypositroid, and let
![]() $L=L_P$
be the corresponding polypositroid loop. The following two sets coincide:
$L=L_P$
be the corresponding polypositroid loop. The following two sets coincide:
-
○ the set of minimal P-membranes,
-
○ the set of minimal membranes with boundary loop L.
Each of these sets is in bijection (via
![]() $M=(G,f)\mapsto G^*$
) with
$M=(G,f)\mapsto G^*$
) with
-
○ the set of reduced plabic graphs with strand permutation
 $\pi _L$
.
$\pi _L$
.
All minimal P-membranes are connected with each other by a sequence of local moves of types (I), (II), and (III).
Proof. Let us show that the boundary loop L of any minimal P-membrane is exactly the polypositroid loop
![]() $L_P$
. Indeed, by Definition 25.1, for each
$L_P$
. Indeed, by Definition 25.1, for each
![]() $i=1,\dots ,n$
, the loop L contains the points
$i=1,\dots ,n$
, the loop L contains the points
![]() $v^{(i)}$
and
$v^{(i)}$
and
![]() $v^{(i+1)}$
connected by a shortest possible piecewise-linear curve with line segments given some roots. Thus, this portion of the loop L between the points
$v^{(i+1)}$
connected by a shortest possible piecewise-linear curve with line segments given some roots. Thus, this portion of the loop L between the points
![]() $v^{(i)}$
and
$v^{(i)}$
and
![]() $v^{(i+1)}$
should contain exactly
$v^{(i+1)}$
should contain exactly
![]() $m_{ij}$
copies of the root
$m_{ij}$
copies of the root
![]() $e_j-e_i$
, for all
$e_j-e_i$
, for all
![]() $j\ne i$
, cf. formulas (6.1) and (6.3) in Section 6. Note that any way to arrange these roots (in each portion of L between
$j\ne i$
, cf. formulas (6.1) and (6.3) in Section 6. Note that any way to arrange these roots (in each portion of L between
![]() $v^{(i)}$
and
$v^{(i)}$
and
![]() $v^{(i+1)}$
) would produce a unimodal loop. So the surface area of the membrane M is given by Proposition 23.8 in terms of the number of alignments and the number of antiexceedances of the permutation
$v^{(i+1)}$
) would produce a unimodal loop. So the surface area of the membrane M is given by Proposition 23.8 in terms of the number of alignments and the number of antiexceedances of the permutation
![]() $\pi $
associated with L (see Definitions 23.5 and 23.7). The number of antiexceedances of
$\pi $
associated with L (see Definitions 23.5 and 23.7). The number of antiexceedances of
![]() $\pi $
equals
$\pi $
equals
![]() $k(\pi )=\sum _{i>j} m_{ij}$
. In order to minimize the surface area of M, we need to maximize the number of alignments
$k(\pi )=\sum _{i>j} m_{ij}$
. In order to minimize the surface area of M, we need to maximize the number of alignments
![]() $A(\pi )$
of
$A(\pi )$
of
![]() $\pi $
. This maximum is achieved if and only if
$\pi $
. This maximum is achieved if and only if
![]() $L=L_P$
. The theorem now follows from Theorem 23.6.
$L=L_P$
. The theorem now follows from Theorem 23.6.
For a balanced digraph on the vertex set
![]() $[n]$
with edge multiplicities
$[n]$
with edge multiplicities
![]() $m_{ij}$
,
$m_{ij}$
,
![]() $i,j\in [n]$
define the number m of edges, the number k of antiexceedances, and the number A of alignments, as follows:
$i,j\in [n]$
define the number m of edges, the number k of antiexceedances, and the number A of alignments, as follows:
 $$ \begin{align*}\begin{array}{l} \displaystyle m :=\sum_{i\neq j} m_{ij}, \qquad k := \sum_{i>j} m_{ij},\\[.1in] \displaystyle A := \sum_{ \scriptsize \begin{array}{l} i<i'<j'<j, \textrm{ or}\\ i'<j'<j<i, \textrm{ or}\\ j'<j<i<i', \textrm{ or}\\ j<i<i'<j' \end{array} } m_{ij}\, m_{i'j'} + \sum_{i,\, j<j'} (m_{ij} m_{ij'} + m_{ji}m_{j'i}) + \sum_{i\neq j} {m_{ij} \choose 2} \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l} \displaystyle m :=\sum_{i\neq j} m_{ij}, \qquad k := \sum_{i>j} m_{ij},\\[.1in] \displaystyle A := \sum_{ \scriptsize \begin{array}{l} i<i'<j'<j, \textrm{ or}\\ i'<j'<j<i, \textrm{ or}\\ j'<j<i<i', \textrm{ or}\\ j<i<i'<j' \end{array} } m_{ij}\, m_{i'j'} + \sum_{i,\, j<j'} (m_{ij} m_{ij'} + m_{ji}m_{j'i}) + \sum_{i\neq j} {m_{ij} \choose 2} \end{array} \end{align*} $$
(notice that we regard a pair of edges of the digraph with the same initial points and/or the same end-points as an alignment). Proposition 23.8 implies the following formulae.
Corollary 25.8. The number of lattice points and the surface area of any minimal P-membrane M are equal to
 $$ \begin{align*}\begin{array}{l} \mathrm{LatticePoints}(M)= k(m-k)-A + 1,\\[.05in] \mathrm{Area}(M) = 2\left(k(m-k)-A\right) - m, \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l} \mathrm{LatticePoints}(M)= k(m-k)-A + 1,\\[.05in] \mathrm{Area}(M) = 2\left(k(m-k)-A\right) - m, \end{array} \end{align*} $$
where m is the number of edges, k is the number of antiexceedances, and A is the number of alignments of the balanced digraph associated with P.

Figure 5 The cactus graph G.
Example 25.9. Let
![]() $n = 4$
. Then
$n = 4$
. Then
![]() $L=$
$L=$
 $$ \begin{align*} &((3,2,1,0),(2,2,1,1),(1,2,2,1),(0,3,2,1), (1,2,2,1),(1,1,2,2), \\ &(1,0,3,2),(1,1,2,2),(2,1,1,2),(2,1,0,3),(2,1,1,2),(2,2,1,1)) \end{align*} $$
$$ \begin{align*} &((3,2,1,0),(2,2,1,1),(1,2,2,1),(0,3,2,1), (1,2,2,1),(1,1,2,2), \\ &(1,0,3,2),(1,1,2,2),(2,1,1,2),(2,1,0,3),(2,1,1,2),(2,2,1,1)) \end{align*} $$
is a polypositroid loop, associated to the balanced digraph, where
![]() $m_{ij} = 1$
for all
$m_{ij} = 1$
for all
![]() $i \neq j$
, studied in Example 6.11. The permutation
$i \neq j$
, studied in Example 6.11. The permutation
![]() $\pi _L: [12] \to [12]$
is given by
$\pi _L: [12] \to [12]$
is given by
and we have
![]() $k(\pi _L) = 6$
. We have
$k(\pi _L) = 6$
. We have
![]() $A = 28$
, and thus for a minimal membrane M, we have
$A = 28$
, and thus for a minimal membrane M, we have
![]() $\mathrm {LatticePoints}(M)= 9$
and
$\mathrm {LatticePoints}(M)= 9$
and
![]() $\mathrm {Area}(M) = 4$
. Let us give an example of a minimal membrane
$\mathrm {Area}(M) = 4$
. Let us give an example of a minimal membrane
![]() $M = (G,\mathit {f})$
. Let G (shown in Figure 5) have boundary vertices
$M = (G,\mathit {f})$
. Let G (shown in Figure 5) have boundary vertices
![]() $\{b_1,\ldots ,b_{12}\}$
arranged clockwise, with repetitions
$\{b_1,\ldots ,b_{12}\}$
arranged clockwise, with repetitions
![]() $b_2 = b_{12} ,b_3=b_5, b_6=b_8, b_9= b_{11}$
, and a single nonboundary vertex b. The edges of G are the boundary edges
$b_2 = b_{12} ,b_3=b_5, b_6=b_8, b_9= b_{11}$
, and a single nonboundary vertex b. The edges of G are the boundary edges
![]() $\{b_i,b_{i+1}\}$
and the edges of the four faces
$\{b_i,b_{i+1}\}$
and the edges of the four faces
![]() $(b,b_2,b_3),(b,b_5,b_6),(b,b_8,b_9),(b,b_{11},b_{12})$
. We define
$(b,b_2,b_3),(b,b_5,b_6),(b,b_8,b_9),(b,b_{11},b_{12})$
. We define
![]() $\mathit {f}(b_i) = \lambda ^{(i)}$
and
$\mathit {f}(b_i) = \lambda ^{(i)}$
and
![]() $\mathit {f} = (2,1,2,1)$
.
$\mathit {f} = (2,1,2,1)$
.
26. Positroid lifts
For a membrane
![]() $M=(G,f)$
and a vertex v of G, let
$M=(G,f)$
and a vertex v of G, let
![]() $f(v)_i$
denote the i-th coordinate of the vector
$f(v)_i$
denote the i-th coordinate of the vector
![]() $f(v)\in \mathbb {Z}^n$
.
$f(v)\in \mathbb {Z}^n$
.
Lemma 26.1. Let
![]() $M=(G,f)$
be a minimal membrane, and let
$M=(G,f)$
be a minimal membrane, and let
![]() $i\in [n]$
. The minimal/maximal value of the i-th coordinate
$i\in [n]$
. The minimal/maximal value of the i-th coordinate
![]() $f(v)_i$
over all vertices v of G is achieved on some boundary vertex
$f(v)_i$
over all vertices v of G is achieved on some boundary vertex
![]() $b_j$
of G.
$b_j$
of G.
Proof. Suppose that this is not true, and the minimal value of the i-th coordinate is achieved on some internal vertex v of G, and it is strictly less than
![]() $f(b_j)_i$
for all boundary vertices
$f(b_j)_i$
for all boundary vertices
![]() $b_j$
. Let
$b_j$
. Let
![]() $F_v$
be the face of the plabic graph
$F_v$
be the face of the plabic graph
![]() $G^*$
that corresponds to the vertex v of G. The i-th coordinate might take the same minimal value on some other vertices of G that correspond to other faces of
$G^*$
that corresponds to the vertex v of G. The i-th coordinate might take the same minimal value on some other vertices of G that correspond to other faces of
![]() $G^*$
adjacent to
$G^*$
adjacent to
![]() $F_v$
. Let R be the maximal connected region formed by such faces of the plabic
$F_v$
. Let R be the maximal connected region formed by such faces of the plabic
![]() $G^*$
. By our assumption, the region R does not include any boundary regions of
$G^*$
. By our assumption, the region R does not include any boundary regions of
![]() $G^*$
, thus the region R is bounded by a closed curve C formed by some edges of
$G^*$
, thus the region R is bounded by a closed curve C formed by some edges of
![]() $G^*$
. Assume that C is oriented clockwise. For any other face of
$G^*$
. Assume that C is oriented clockwise. For any other face of
![]() $G^*$
adjacent to R, the i-th coordinate is strictly greater. This mean that, for any edge
$G^*$
adjacent to R, the i-th coordinate is strictly greater. This mean that, for any edge
![]() $a\to b$
of
$a\to b$
of
![]() $G^*$
on the curve C (oriented in same the clockwise direction), the strand S that passes through the edge
$G^*$
on the curve C (oriented in same the clockwise direction), the strand S that passes through the edge
![]() $a\to b$
has label
$a\to b$
has label
![]() $g(S)=i$
; see Theorem 21.5. Since any two intersecting strands cannot have the same label, we conclude that all edges on the closed curve C belong to the same strand S. This means that the strand S is either self-intersecting or closed. Since the membrane M is minimal, the plabic graph
$g(S)=i$
; see Theorem 21.5. Since any two intersecting strands cannot have the same label, we conclude that all edges on the closed curve C belong to the same strand S. This means that the strand S is either self-intersecting or closed. Since the membrane M is minimal, the plabic graph
![]() $G^*$
is reduced (see Theorem 23.3). However, by Definition 23.1, a reduced plabic graph cannot contain self-intersecting or closed strands. We obtain a contradiction. The proof of the claim about the maximal value of
$G^*$
is reduced (see Theorem 23.3). However, by Definition 23.1, a reduced plabic graph cannot contain self-intersecting or closed strands. We obtain a contradiction. The proof of the claim about the maximal value of
![]() $f(v)_i$
is analogous.
$f(v)_i$
is analogous.
Let
![]() $\mathbf {d}=(d_1,\dots ,d_n)$
be a nonnegative integer vector. We say that a loop
$\mathbf {d}=(d_1,\dots ,d_n)$
be a nonnegative integer vector. We say that a loop
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})\in (\mathbb {Z}^n)^m$
is
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})\in (\mathbb {Z}^n)^m$
is
![]() $\mathbf {d}$
-boxed if
$\mathbf {d}$
-boxed if
![]() $\min _{j\in [m]} \lambda ^{(j)}_i = 0$
and
$\min _{j\in [m]} \lambda ^{(j)}_i = 0$
and
![]() $\max _{j\in [m]} \lambda ^{(j)}_i = d_i$
, for all
$\max _{j\in [m]} \lambda ^{(j)}_i = d_i$
, for all
![]() $i\in [n]$
. In other words, the curve
$i\in [n]$
. In other words, the curve
![]() $\left <L\right>$
lies in the box
$\left <L\right>$
lies in the box
![]() $[0,d_1]\times \cdots \times [0,d_n]\subset \mathbb {R}^n$
and has points on each facet of the box.
$[0,d_1]\times \cdots \times [0,d_n]\subset \mathbb {R}^n$
and has points on each facet of the box.
According to Lemma 26.1, for any minimal membrane M with a
![]() $\mathbf {d}$
-boxed boundary loop L, we have
$\mathbf {d}$
-boxed boundary loop L, we have
![]() $\left <M\right>\subset [0,d_1]\times \cdots \times [0,d_n]$
. Moreover, both
$\left <M\right>\subset [0,d_1]\times \cdots \times [0,d_n]$
. Moreover, both
![]() $\left <L\right>$
and
$\left <L\right>$
and
![]() $\left <M\right>$
belong to the intersection of the box
$\left <M\right>$
belong to the intersection of the box
![]() $[0,d_1]\times \cdots \times [0,d_n]$
with some affine hyperplane
$[0,d_1]\times \cdots \times [0,d_n]$
with some affine hyperplane
![]() $x_1+\cdots + x_n = k$
.
$x_1+\cdots + x_n = k$
.
Definition 26.2. Let
![]() $d=d_1+\cdots +d_n$
. For an integer vector
$d=d_1+\cdots +d_n$
. For an integer vector
![]() $\lambda =(\lambda _1,\dots ,\lambda _n) \in [0,d_1]\times \cdots \times [0,d_n]$
, let
$\lambda =(\lambda _1,\dots ,\lambda _n) \in [0,d_1]\times \cdots \times [0,d_n]$
, let
![]() $\mathrm {lift}(\lambda )$
be the 0-1-vector in
$\mathrm {lift}(\lambda )$
be the 0-1-vector in
![]() $\mathbb {Z}^d$
given by
$\mathbb {Z}^d$
given by
where
![]() $a^r$
denotes a repeated r times.
$a^r$
denotes a repeated r times.
Let
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})\in (\mathbb {Z}^n)^m$
be a
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})\in (\mathbb {Z}^n)^m$
be a
![]() $\mathbf {d}$
-boxed loop. The lift of L is the loop
$\mathbf {d}$
-boxed loop. The lift of L is the loop
![]() $\mathrm {lift}(L):=(\mathrm {lift}(\lambda ^{(1)}),\dots ,\mathrm {lift}(\lambda ^{(m)})) \in (\mathbb {Z}^d)^m$
.
$\mathrm {lift}(L):=(\mathrm {lift}(\lambda ^{(1)}),\dots ,\mathrm {lift}(\lambda ^{(m)})) \in (\mathbb {Z}^d)^m$
.
For a minimal membrane
![]() $M=(G,f)$
with boundary loop L, the lift of M is the membrane
$M=(G,f)$
with boundary loop L, the lift of M is the membrane
![]() $\mathrm {lift}(M) := (G,\mathrm {lift}(f))$
, where
$\mathrm {lift}(M) := (G,\mathrm {lift}(f))$
, where
![]() $\mathrm {lift}(f): v\mapsto \mathrm {lift}(f(v))\in \mathbb {Z}^d$
, for a vertex v of G.
$\mathrm {lift}(f): v\mapsto \mathrm {lift}(f(v))\in \mathbb {Z}^d$
, for a vertex v of G.
Let
![]() $\mathrm {proj}:\mathbb {R}^d\to \mathbb {R}^n$
be the mapFootnote 8 given by
$\mathrm {proj}:\mathbb {R}^d\to \mathbb {R}^n$
be the mapFootnote 8 given by
For a membrane
![]() $\tilde M = (G,\tilde f)$
, where
$\tilde M = (G,\tilde f)$
, where
![]() $f:{\mathrm {Vert}}\to \mathbb {Z}^d$
, define
$f:{\mathrm {Vert}}\to \mathbb {Z}^d$
, define
![]() $\mathrm {proj}(\tilde M) := (G, \mathrm {proj}(\tilde f))$
.
$\mathrm {proj}(\tilde M) := (G, \mathrm {proj}(\tilde f))$
.
Proposition 26.3. Let
![]() $L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})\in (\mathbb {Z}^n)^m$
be a
$L=(\lambda ^{(1)},\dots ,\lambda ^{(m)})\in (\mathbb {Z}^n)^m$
be a
![]() $\mathbf {d}$
-boxed unimodal loop. Then
$\mathbf {d}$
-boxed unimodal loop. Then
![]() $m=d:=d_1+\cdots + d_n$
. The sequence of roots
$m=d:=d_1+\cdots + d_n$
. The sequence of roots
![]() $e_{i_a}-e_{j_a} = \mathrm {lift}(\lambda ^{(a+1)})-\mathrm {lift}(\lambda ^{(a)})\in \mathbb {Z}^m$
,
$e_{i_a}-e_{j_a} = \mathrm {lift}(\lambda ^{(a+1)})-\mathrm {lift}(\lambda ^{(a)})\in \mathbb {Z}^m$
,
![]() $a=1,\dots ,m$
, associated with the loop
$a=1,\dots ,m$
, associated with the loop
![]() $\mathrm {lift}(L)$
satisfies the condition: both sequences
$\mathrm {lift}(L)$
satisfies the condition: both sequences
![]() $i_1,\dots ,i_m$
and
$i_1,\dots ,i_m$
and
![]() $j_1,\dots ,j_m$
are permutations of
$j_1,\dots ,j_m$
are permutations of
![]() $1,\dots ,m$
.
$1,\dots ,m$
.
The following three sets are in bijection with each other:
-
○ Minimal membranes M with boundary loop L.
-
○ Minimal membranes
 $\tilde M$
with boundary loop
$\tilde M$
with boundary loop
 $\mathrm {lift}(L)$
.
$\mathrm {lift}(L)$
. -
○ Reduced plabic graphs
 $G^*$
with strand permutation
$G^*$
with strand permutation
 $\pi _L$
(see Definition 23.5).
$\pi _L$
(see Definition 23.5).
Explicitly, the bijections are given by the maps (which form a commutative diagram):
![]() $M\mapsto \tilde M = \mathrm {lift}(M)$
,
$M\mapsto \tilde M = \mathrm {lift}(M)$
,
![]() $\tilde M\mapsto M = \mathrm {proj}(\tilde M)$
,
$\tilde M\mapsto M = \mathrm {proj}(\tilde M)$
,
![]() $M=(G,f) \mapsto G^*$
,
$M=(G,f) \mapsto G^*$
,
![]() $\tilde M=(G,\tilde f) \mapsto G^*$
.
$\tilde M=(G,\tilde f) \mapsto G^*$
.
The loop
![]() $\mathrm {lift}(L)$
is obtained from a positroid loop in
$\mathrm {lift}(L)$
is obtained from a positroid loop in
![]() $\mathbb {Z}^m$
by a permutation of coordinates in
$\mathbb {Z}^m$
by a permutation of coordinates in
![]() $\mathbb {Z}^m$
. This is exactly the positroid whose permutation is equal to
$\mathbb {Z}^m$
. This is exactly the positroid whose permutation is equal to
![]() $\pi _L$
. Thus, the lifted membranes
$\pi _L$
. Thus, the lifted membranes
![]() $\tilde M$
are permuted positroid membranes.
$\tilde M$
are permuted positroid membranes.
Proof. The first claim easily follows from the definitions. The claim about bijections between the sets of membranes M,
![]() $\tilde M$
, and reduced plabic graphs
$\tilde M$
, and reduced plabic graphs
![]() $G^*$
follows from Theorem 23.6. Indeed, both loops L and
$G^*$
follows from Theorem 23.6. Indeed, both loops L and
![]() $\mathrm {lift}(L)$
correspond to the same permutation
$\mathrm {lift}(L)$
correspond to the same permutation
![]() $\pi _L = \pi _{\mathrm {lift}(L)}$
(see Definition 23.5).
$\pi _L = \pi _{\mathrm {lift}(L)}$
(see Definition 23.5).
Let us specialize this construction to polypositroid loops. As in the previous section, let
![]() $P\subset \mathbb {R}^n$
be an integer polypositroid. Assume that P belongs to the positive orthant
$P\subset \mathbb {R}^n$
be an integer polypositroid. Assume that P belongs to the positive orthant
![]() $\mathbb {R}_{\geq 0}^n$
and has points on each coordinate plane in
$\mathbb {R}_{\geq 0}^n$
and has points on each coordinate plane in
![]() $\mathbb {R}^n$
. Let
$\mathbb {R}^n$
. Let
![]() $m_{ij}$
be the edge multiplicities of the balanced digraph associated with P, let
$m_{ij}$
be the edge multiplicities of the balanced digraph associated with P, let
![]() $m :=\sum _{i,j} m_{ij}$
be the total number of edges of the digraph, let
$m :=\sum _{i,j} m_{ij}$
be the total number of edges of the digraph, let
![]() $k=\sum _{i>j} m_{ij}$
be its number of antiexceedances, and let
$k=\sum _{i>j} m_{ij}$
be its number of antiexceedances, and let
![]() $d_i := \sum _{j} m_{ij}$
,
$d_i := \sum _{j} m_{ij}$
,
![]() $i\in [n]$
, be the outdegrees (or the indegrees) of the balanced digraph. Clearly, we have
$i\in [n]$
, be the outdegrees (or the indegrees) of the balanced digraph. Clearly, we have
![]() $m=d_1+\cdots + d_n$
. Let
$m=d_1+\cdots + d_n$
. Let
![]() $\mathbf {d}=(d_1,\dots ,d_n)$
.
$\mathbf {d}=(d_1,\dots ,d_n)$
.
Corollary 26.4. For a polypositroid P as above, the polypositroid loop
![]() $L=L_P$
is
$L=L_P$
is
![]() $\mathbf {d}$
-boxed. Its lift
$\mathbf {d}$
-boxed. Its lift
![]() $\mathrm {lift}(L)$
is a positroid loop in
$\mathrm {lift}(L)$
is a positroid loop in
![]() $\mathbb {Z}^m$
.
$\mathbb {Z}^m$
.
The maps
![]() $\mathrm {lift}:M\mapsto \tilde M$
and
$\mathrm {lift}:M\mapsto \tilde M$
and
![]() $\mathrm {proj}:\tilde M\mapsto M$
give a bijection between minimal membranes M with boundary loop L minimal positroid membranes
$\mathrm {proj}:\tilde M\mapsto M$
give a bijection between minimal membranes M with boundary loop L minimal positroid membranes
![]() $\tilde M$
with boundary loop
$\tilde M$
with boundary loop
![]() $\mathrm {lift}(L)$
.
$\mathrm {lift}(L)$
.
The first claims in this statement are straightforward from the definitions, the last claim is a special case of Proposition 26.3.
Example 26.5. Consider the polypositroid loop L in Example 25.9. Then L is
![]() $\mathbf {d}=(3,3,3,3)$
-boxed, and
$\mathbf {d}=(3,3,3,3)$
-boxed, and
 $$ \begin{align*} \mathrm{lift}(L)= &((1,1,1,0,1,1,0,0,1,0,0,0),(0,1,1,0,1,1,0,0,1,0,0,1), \\ &(0,0,1,0,1,1,0,1,1,0,0,1),(0,0,0,1,1,1,0,1,1,0,0,1), \ldots). \end{align*} $$
$$ \begin{align*} \mathrm{lift}(L)= &((1,1,1,0,1,1,0,0,1,0,0,0),(0,1,1,0,1,1,0,0,1,0,0,1), \\ &(0,0,1,0,1,1,0,1,1,0,0,1),(0,0,0,1,1,1,0,1,1,0,0,1), \ldots). \end{align*} $$
Let
![]() ${\mathcal {M}}\subset {[m]\choose k}$
be the positroid associated with the positroid loop
${\mathcal {M}}\subset {[m]\choose k}$
be the positroid associated with the positroid loop
![]() $\mathrm {lift}(L)$
, and let
$\mathrm {lift}(L)$
, and let
![]() $P_{\mathcal {M}}:=\mathrm {conv}(e_I\mid I \in {\mathcal {M}}\}\subset \mathbb {R}^m$
be the positroid polytope of the positroid
$P_{\mathcal {M}}:=\mathrm {conv}(e_I\mid I \in {\mathcal {M}}\}\subset \mathbb {R}^m$
be the positroid polytope of the positroid
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
Lemma 26.6. Under the map
![]() $\mathrm {proj}:\mathbb {R}^m\to \mathbb {R}^n$
, we have
$\mathrm {proj}:\mathbb {R}^m\to \mathbb {R}^n$
, we have
![]() $\mathrm {proj}(P_{\mathcal {M}})\subseteq P$
.
$\mathrm {proj}(P_{\mathcal {M}})\subseteq P$
.
Proof. The positroid polytope
![]() $P_{\mathcal {M}}$
, being an alcoved polytope in
$P_{\mathcal {M}}$
, being an alcoved polytope in
![]() $\mathbb {R}^m$
, is given by inequalities of the form
$\mathbb {R}^m$
, is given by inequalities of the form
![]() $x_i+x_{i+1} + \cdots + x_j \leq c_{ij}$
for all cyclic intervals
$x_i+x_{i+1} + \cdots + x_j \leq c_{ij}$
for all cyclic intervals
![]() $[i,j]$
in
$[i,j]$
in
![]() $[m]$
. Similarly, the polytope P, being an alcoved polytope in
$[m]$
. Similarly, the polytope P, being an alcoved polytope in
![]() $\mathbb {R}^n$
, is given by inequalities of the form
$\mathbb {R}^n$
, is given by inequalities of the form
![]() $y_a+y_{a+1}+\cdots + y_b \leq d_{ab}$
for all cyclic intervals
$y_a+y_{a+1}+\cdots + y_b \leq d_{ab}$
for all cyclic intervals
![]() $[a,b]$
in
$[a,b]$
in
![]() $[n]$
. One can check from the definitions that the inequalities for
$[n]$
. One can check from the definitions that the inequalities for
![]() $P_{\mathcal {M}}$
corresponding to cyclic intervals
$P_{\mathcal {M}}$
corresponding to cyclic intervals
![]() $[i,j]$
that consist of unions of blocks
$[i,j]$
that consist of unions of blocks
![]() $\{1,\dots ,d_1\}$
,
$\{1,\dots ,d_1\}$
,
![]() $\{d_1+1,\dots ,d_1+d_2\}$
, etc., project exactly to the inequalities defining the polytope P.
$\{d_1+1,\dots ,d_1+d_2\}$
, etc., project exactly to the inequalities defining the polytope P.
Theorem 24.1 now implies the following claim.
Corollary 26.7. For any minimal P-membrane M, the embedding
![]() $\left <M\right>\subset \mathbb {R}^n$
belongs to the polypositroid:
$\left <M\right>\subset \mathbb {R}^n$
belongs to the polypositroid:
![]() $\left <M\right>\subset P$
.
$\left <M\right>\subset P$
.
Remark 26.8. The same plabic graph
![]() $G^*$
can appear in different membranes
$G^*$
can appear in different membranes
![]() $M=(G,f)$
of different dimensions. For any reduced plabic graph
$M=(G,f)$
of different dimensions. For any reduced plabic graph
![]() $G^*$
with m boundary edges, there is always the associated positroid membrane of dimension
$G^*$
with m boundary edges, there is always the associated positroid membrane of dimension
![]() $m-1$
that lies in a hyperplane
$m-1$
that lies in a hyperplane
![]() $\{x_1+\cdots + x_m = k\}\subset \mathbb {R}^m$
. But there might also be other lower dimensional membranes with the same plabic graph, which are obtained by projections of this positroid membrane.
$\{x_1+\cdots + x_m = k\}\subset \mathbb {R}^m$
. But there might also be other lower dimensional membranes with the same plabic graph, which are obtained by projections of this positroid membrane.
Define the essential dimension of a reduced plabic graph
![]() $G^*$
as the minimal dimension of a minimal membrane whose plabic graph is equal to
$G^*$
as the minimal dimension of a minimal membrane whose plabic graph is equal to
![]() $G^*$
.
$G^*$
.
Proposition 26.9. For a reduced plabic graph
![]() $G^*$
with m boundary edges, the essential dimension equals
$G^*$
with m boundary edges, the essential dimension equals
![]() $m-1$
if and only if
$m-1$
if and only if
![]() $G^*$
is a plabic graph for the top positroid cell in
$G^*$
is a plabic graph for the top positroid cell in
![]() $\mathrm {Gr}(k,m)_{\geq 0}$
for some
$\mathrm {Gr}(k,m)_{\geq 0}$
for some
![]() $k\in [m-1]$
, that is, if its strand permutation is
$k\in [m-1]$
, that is, if its strand permutation is
![]() $\pi :i\mapsto i+k\pmod m$
.
$\pi :i\mapsto i+k\pmod m$
.
Proof. If a graph
![]() $G^*$
has a maximal possible essential dimension
$G^*$
has a maximal possible essential dimension
![]() $m-1$
, then its strand permutation
$m-1$
, then its strand permutation
![]() $\pi $
does not have alignments. Indeed, if
$\pi $
does not have alignments. Indeed, if
![]() $\pi $
has an alignment
$\pi $
has an alignment
![]() $(i,j)$
, then we can project the positroid membrane for
$(i,j)$
, then we can project the positroid membrane for
![]() $G^*$
to a lower-dimensional membrane by mapping
$G^*$
to a lower-dimensional membrane by mapping
![]() $(x_i,x_j)\mapsto x_i + x_j$
and leaving all other coordinates. The only permutations with no alignments are permutations given by
$(x_i,x_j)\mapsto x_i + x_j$
and leaving all other coordinates. The only permutations with no alignments are permutations given by
![]() $\pi :i\mapsto i+k\pmod m$
, for some k.
$\pi :i\mapsto i+k\pmod m$
, for some k.
Assume now that
![]() $G^*$
is a plabic graph for the top positroid cell in
$G^*$
is a plabic graph for the top positroid cell in
![]() $\mathrm {Gr}(k,m)_{\geq 0}$
and
$\mathrm {Gr}(k,m)_{\geq 0}$
and
![]() $M=(G,f)$
is a minimal membrane with
$M=(G,f)$
is a minimal membrane with
![]() $f:{\mathrm {Vert}} \to \mathbb {Z}^n$
. If
$f:{\mathrm {Vert}} \to \mathbb {Z}^n$
. If
![]() $n<m$
, then we can find two different strands S and T in
$n<m$
, then we can find two different strands S and T in
![]() $G^*$
, with the same label
$G^*$
, with the same label
![]() $g(S)=g(T)$
(see Theorem 21.5). According to Theorem 21.5, the strands S and T can not intersect in the plabic graph
$g(S)=g(T)$
(see Theorem 21.5). According to Theorem 21.5, the strands S and T can not intersect in the plabic graph
![]() $G^*$
. It is not hard to show, using the techniques of [Reference PostnikovPo06], that for any i and j, there is some plabic graph for the top cell in
$G^*$
. It is not hard to show, using the techniques of [Reference PostnikovPo06], that for any i and j, there is some plabic graph for the top cell in
![]() $\mathrm {Gr}(k,m)_{\geq 0}$
whose i-th and j-th strands intersect. Also, according to Theorem 23.2 ([Reference PostnikovPo06, Theorem 13.4]), all plabic graphs for the top cell are connected with each other by local moves. This means that even if the strands S and T do not intersect in
$\mathrm {Gr}(k,m)_{\geq 0}$
whose i-th and j-th strands intersect. Also, according to Theorem 23.2 ([Reference PostnikovPo06, Theorem 13.4]), all plabic graphs for the top cell are connected with each other by local moves. This means that even if the strands S and T do not intersect in
![]() $G^*$
, one can always find a sequence of local moves that result in a plabic graph, where the pair strands with the same sources and targets as S and T intersect each other. Since local moves preserve minimal membranes, we deduce that for two different strands, we cannot have
$G^*$
, one can always find a sequence of local moves that result in a plabic graph, where the pair strands with the same sources and targets as S and T intersect each other. Since local moves preserve minimal membranes, we deduce that for two different strands, we cannot have
![]() $g(S)=g(T)$
. Thus,
$g(S)=g(T)$
. Thus,
![]() $n=m$
.
$n=m$
.
Reduced plabic graphs of essential dimension 2 are the bipartite plabic graphs that can be drawn on the plane as subgraphs of the regular hexagonal lattice.
27. Semisimple membranes
Recall (e.g., see [Reference HumphreysHum]), that for a Coxeter element
![]() $c\in W$
in the Weyl group associated with root system
$c\in W$
in the Weyl group associated with root system
![]() $R\subset V\simeq \mathbb {R}^r$
, there exists a unique 2-dimensional plane
$R\subset V\simeq \mathbb {R}^r$
, there exists a unique 2-dimensional plane
![]() $P\subset V$
,
$P\subset V$
,
![]() $P\simeq \mathbb {R}^2$
, called the Coxeter plane, such that P is c-invariant, and the Coxeter element c acts on P by rotations by
$P\simeq \mathbb {R}^2$
, called the Coxeter plane, such that P is c-invariant, and the Coxeter element c acts on P by rotations by
![]() $2\pi /h$
. Note that the Coxeter element c defines an orientation on the Coxeter plane P, assuming that c acts on P by a clockwise rotation. Let
$2\pi /h$
. Note that the Coxeter element c defines an orientation on the Coxeter plane P, assuming that c acts on P by a clockwise rotation. Let
![]() $p:V\to P$
be the orthogonal projection onto the Coxeter plane.
$p:V\to P$
be the orthogonal projection onto the Coxeter plane.
Definition 27.1. Fix a Coxeter element
![]() $c\in W$
. We say that an R-membrane M is semisimple if the projection
$c\in W$
. We say that an R-membrane M is semisimple if the projection
![]() $p:\left <M\right>\to p(\left <M\right>)$
onto the Coxeter plane is a bijective map between
$p:\left <M\right>\to p(\left <M\right>)$
onto the Coxeter plane is a bijective map between
![]() $\left <M\right>$
and
$\left <M\right>$
and
![]() $p(\left <M\right>)$
and each component of the projection
$p(\left <M\right>)$
and each component of the projection
![]() $p(\left <L\right>)$
of the boundary loop L of M is oriented clockwise in the Coxeter plane.
$p(\left <L\right>)$
of the boundary loop L of M is oriented clockwise in the Coxeter plane.
Equivalently, an R-membrane
![]() $M=(G,f)$
is semisimple if the orientation of any triangle
$M=(G,f)$
is semisimple if the orientation of any triangle
![]() $\Delta $
in the cactus G agrees with the orientation of the projection
$\Delta $
in the cactus G agrees with the orientation of the projection
![]() $p(\left <\Delta \right>)$
in the Coxeter plane.
$p(\left <\Delta \right>)$
in the Coxeter plane.
Example 27.2. Consider the
![]() $B_4$
-membrane in Example 20.4. This membrane is not semisimple: the two faces
$B_4$
-membrane in Example 20.4. This membrane is not semisimple: the two faces
![]() $(b, b_ 2, b_ 3), (b, b_ 3, b_ 6)$
are oppositely oriented in the Coxeter plane. Here, the Coxeter plane can be taken to be the span of the real and imaginary parts of
$(b, b_ 2, b_ 3), (b, b_ 3, b_ 6)$
are oppositely oriented in the Coxeter plane. Here, the Coxeter plane can be taken to be the span of the real and imaginary parts of
![]() $v = (1,\eta ,\eta ^2,\eta ^3)$
, where
$v = (1,\eta ,\eta ^2,\eta ^3)$
, where
![]() $\eta $
is a primitive 8-th root of unity.
$\eta $
is a primitive 8-th root of unity.
Remark 27.3. A simple membrane M is a semisimple membrane, such that
![]() $\left <M\right>\simeq p(\left <M\right>)$
is homeomorphic to a disk (or to a line segment when
$\left <M\right>\simeq p(\left <M\right>)$
is homeomorphic to a disk (or to a line segment when
![]() $m=2$
). A semisimple membrane is simple if and only if the graph
$m=2$
). A semisimple membrane is simple if and only if the graph
![]() $G^*$
is connected. Any semisimple membrane is obtained by taking wedges of simple membranes along their boundary vertices.
$G^*$
is connected. Any semisimple membrane is obtained by taking wedges of simple membranes along their boundary vertices.
Let us now discuss the type A case. Assume that
![]() $c=(12\cdots n)\in S_n$
is the standard long cycle in
$c=(12\cdots n)\in S_n$
is the standard long cycle in
![]() $S_n$
, which is a Coxeter element in type A case. We can identify the corresponding Coxeter plane with
$S_n$
, which is a Coxeter element in type A case. We can identify the corresponding Coxeter plane with
![]() $\mathbb {R}^2$
and assume that
$\mathbb {R}^2$
and assume that
is the projection that sends the coordinate vectors
![]() $e_1,\dots ,e_n$
in
$e_1,\dots ,e_n$
in
![]() $\mathbb {R}^n$
to the vertices
$\mathbb {R}^n$
to the vertices
![]() $u_1,\dots ,u_n$
of a regular n-gon in
$u_1,\dots ,u_n$
of a regular n-gon in
![]() $\mathbb {R}^2$
centered at the origin
$\mathbb {R}^2$
centered at the origin
![]() $0$
arranged in the clockwise order.
$0$
arranged in the clockwise order.
Recall that a loop
![]() $L =(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
, with
$L =(\lambda ^{(1)},\dots ,\lambda ^{(m)})$
, with
![]() $\lambda ^{(a+1)}-\lambda ^{(a)}=e_{i_a}-e_{j_a}$
, for
$\lambda ^{(a+1)}-\lambda ^{(a)}=e_{i_a}-e_{j_a}$
, for
![]() $a\in \mathbb {Z}/m\mathbb {Z}$
, is called j-increasing if
$a\in \mathbb {Z}/m\mathbb {Z}$
, is called j-increasing if
![]() $j_1\leq j_2 \leq \cdots \leq j_m$
. In particular, any polypositroid loop is j-increasing.
$j_1\leq j_2 \leq \cdots \leq j_m$
. In particular, any polypositroid loop is j-increasing.
Theorem 27.4. Let L be any j-increasing polypositroid loop. A membrane M with boundary loop L is minimal if and only if M is semisimple.
Proof. Let
![]() $M=(G,f)$
be a minimal membrane with boundary loop L. So the plabic graph
$M=(G,f)$
be a minimal membrane with boundary loop L. So the plabic graph
![]() $G^*$
is reduced. Let
$G^*$
is reduced. Let
![]() $\Delta $
be any triangle in the cactus G, let d be the corresponding vertex in the plabic graph
$\Delta $
be any triangle in the cactus G, let d be the corresponding vertex in the plabic graph
![]() $G^*$
, and let
$G^*$
, and let
![]() $S_1, S_2, S_3$
be the three strands in
$S_1, S_2, S_3$
be the three strands in
![]() $G^*$
that pass through the three edges of
$G^*$
that pass through the three edges of
![]() $G^*$
adjacent to the vertex d in the directions away from d arranged, respectively, in the clockwise order. Since
$G^*$
adjacent to the vertex d in the directions away from d arranged, respectively, in the clockwise order. Since
![]() $G^*$
is a reduced plabic graph, the segments of these three strands between the vertex d and their target points
$G^*$
is a reduced plabic graph, the segments of these three strands between the vertex d and their target points
![]() $t_1,t_2,t_3$
on the boundary of the disk cannot intersect each other. So the three target points
$t_1,t_2,t_3$
on the boundary of the disk cannot intersect each other. So the three target points
![]() $t_1,t_2,t_3$
of the strands
$t_1,t_2,t_3$
of the strands
![]() $S_1,S_2,S_3$
, respectively, are arranged in the clockwise order on the boundary of the disk. Thus, the labels
$S_1,S_2,S_3$
, respectively, are arranged in the clockwise order on the boundary of the disk. Thus, the labels
![]() $g(S_1), g(S_2), g(S_3)\in [n]$
of these three strands (which are
$g(S_1), g(S_2), g(S_3)\in [n]$
of these three strands (which are
![]() $j_{t_1}, j_{t_2}, j_{t_3}$
, respectively; see Theorem 21.5) are ordered as
$j_{t_1}, j_{t_2}, j_{t_3}$
, respectively; see Theorem 21.5) are ordered as
![]() $g(S_1)<g(S_2)< g(S_3)$
(up to a cyclic shift).
$g(S_1)<g(S_2)< g(S_3)$
(up to a cyclic shift).
The triangle
![]() $\Delta $
is embedded into
$\Delta $
is embedded into
![]() $\mathbb {R}^n$
either as
$\mathbb {R}^n$
either as
![]() $\mathrm {conv}(-e_{g(S_1)}, -e_{g(S_2)}, -e_{g(S_3)})$
or as
$\mathrm {conv}(-e_{g(S_1)}, -e_{g(S_2)}, -e_{g(S_3)})$
or as
![]() $\mathrm {conv}(e_{g(S_1)}, e_{g(S_2)}, e_{g(S_3)})$
(up to a parallel translation) depending on the color of the triangle. In both cases, the rules of the road imply that the orientation of the triangle
$\mathrm {conv}(e_{g(S_1)}, e_{g(S_2)}, e_{g(S_3)})$
(up to a parallel translation) depending on the color of the triangle. In both cases, the rules of the road imply that the orientation of the triangle
![]() $\Delta $
in the cactus G agrees with the orientation of the projection
$\Delta $
in the cactus G agrees with the orientation of the projection
![]() $p(\left <\Delta \right>)$
onto the Coxeter plane. This implies that the membrane M is semisimple.
$p(\left <\Delta \right>)$
onto the Coxeter plane. This implies that the membrane M is semisimple.
On the other hand, let us now assume that M is a semisimple membrane and deduce that it should be a minimal membrane. Whenever we apply a local move to M, it remains semisimple. Indeed, for a square move (II), that is, an octahedron move shown on Figure 4, if the upper half of the surface of the octahedron projects bijectively onto the Coxeter plane, then the lower part of the surface projects bijectively onto the Coxeter plane. For a tetrahedron move, that is, a move of type (I) or (III) shown on Figure 4, observe that the four vertices of the two triangles involved in the move project onto the Coxeter plane as some points
![]() $u_i +v , u_j + v , u_k + v , u_l +v$
. Since
$u_i +v , u_j + v , u_k + v , u_l +v$
. Since
![]() $u_1,\ldots ,u_n$
are vertices of a convex n-gon, it is impossible that one of these four points lies in the convex hull of the three other points. Thus, if the union of two triangles involved in a move of type (I) or (III) projects bijectively onto the Coxeter plane, then the same remains true after the move.
$u_1,\ldots ,u_n$
are vertices of a convex n-gon, it is impossible that one of these four points lies in the convex hull of the three other points. Thus, if the union of two triangles involved in a move of type (I) or (III) projects bijectively onto the Coxeter plane, then the same remains true after the move.
If M is not minimal, then we can find a sequence of local moves that results in a plabic graph with a pair of parallel edges and a membrane with two coinciding triangles
![]() $\left <\Delta \right>=\left <\Delta '\right>$
. However, in a semisimple membrane, two triangles cannot coincide. Thus, M should be a minimal membrane.
$\left <\Delta \right>=\left <\Delta '\right>$
. However, in a semisimple membrane, two triangles cannot coincide. Thus, M should be a minimal membrane.
Remark 27.5. For a positroid
![]() ${\mathcal {M}}$
, projections of minimal membranes with boundary loop
${\mathcal {M}}$
, projections of minimal membranes with boundary loop
![]() $L_{\mathcal {M}}$
onto the Coxeter plane are related to the plabic tilings of Oh et al. [Reference Oh, Postnikov and SpeyerOPS]. Plabic tilings are certain subdivisions (or tilings) of a polygon on the plane into smaller polygons (or tiles) colored in two colors. The tiles are not necessarily triangles. A plabic tiling corresponds to an equivalence class under moves of types (I) and (III) of projections of minimal membranes with boundary loop
$L_{\mathcal {M}}$
onto the Coxeter plane are related to the plabic tilings of Oh et al. [Reference Oh, Postnikov and SpeyerOPS]. Plabic tilings are certain subdivisions (or tilings) of a polygon on the plane into smaller polygons (or tiles) colored in two colors. The tiles are not necessarily triangles. A plabic tiling corresponds to an equivalence class under moves of types (I) and (III) of projections of minimal membranes with boundary loop
![]() $L_{\mathcal {M}}$
onto the Coxeter plane. In other words, a plabic tiling is obtained from a projection of a membrane by combining its adjacent triangles colored in the same color into tiles.
$L_{\mathcal {M}}$
onto the Coxeter plane. In other words, a plabic tiling is obtained from a projection of a membrane by combining its adjacent triangles colored in the same color into tiles.
28. Higher octahedron recurrence and cluster algebras
Consider the collection of variables
![]() $x_{\lambda }$
, labelled by integer vectors
$x_{\lambda }$
, labelled by integer vectors
![]() $\lambda \in \mathbb {Z}^n$
, that satisfy the following higher octahedron relations:
$\lambda \in \mathbb {Z}^n$
, that satisfy the following higher octahedron relations:
for any
![]() $i<j<k<l$
in
$i<j<k<l$
in
![]() $[n]$
, and any
$[n]$
, and any
![]() $\lambda \in \mathbb {Z}^n$
. We will call the recurrence (28.1) the higher octahedron recurrence. The polytope
$\lambda \in \mathbb {Z}^n$
. We will call the recurrence (28.1) the higher octahedron recurrence. The polytope
![]() $\mathrm {conv}(e_i+e_k, e_j+e_l, e_i+e_j, e_k+e_l, e_i+e_l, e_j+e_k)$
is an octahedron in
$\mathrm {conv}(e_i+e_k, e_j+e_l, e_i+e_j, e_k+e_l, e_i+e_l, e_j+e_k)$
is an octahedron in
![]() $\mathbb {R}^n$
, which explains the name of the above relations.
$\mathbb {R}^n$
, which explains the name of the above relations.
Clearly, each relation (28.1) involves only the variables
![]() $x_{\lambda }$
, for
$x_{\lambda }$
, for
![]() $\lambda $
in an affine hyperplane
$\lambda $
in an affine hyperplane
![]() $\{\lambda _1+\cdots +\lambda _n= \mathrm {Const}\}$
. So, essentially, (28.1) is a recurrence relation on variables corresponding to points of the
$\{\lambda _1+\cdots +\lambda _n= \mathrm {Const}\}$
. So, essentially, (28.1) is a recurrence relation on variables corresponding to points of the
![]() $(n-1)$
-dimensional integer lattice. For
$(n-1)$
-dimensional integer lattice. For
![]() $n=4$
, this recurrence on
$n=4$
, this recurrence on
![]() $\mathbb {Z}^3$
is equivalent to the octahedron recurrence (see, for example [Reference SpeyerSpe]).
$\mathbb {Z}^3$
is equivalent to the octahedron recurrence (see, for example [Reference SpeyerSpe]).
Let us now define algebras generated by certain finite subsets of variables
![]() $x_{\lambda }$
satisfying the octahedron relations.
$x_{\lambda }$
satisfying the octahedron relations.
Definition 28.1. For a loop
![]() $L\subset \mathbb {Z}^n$
, define its cloud as the union of integer lattice points of
$L\subset \mathbb {Z}^n$
, define its cloud as the union of integer lattice points of
![]() $\left <M\right>$
over all minimal membranes M with boundary loop L:
$\left <M\right>$
over all minimal membranes M with boundary loop L:
 $$ \begin{align*}\mathrm{cloud}(L) : = \bigcup_{M = (G,f) \textrm{ min. membr. with bound. }L } \{f(v)\mid v \textrm{ is vertex of } G\}. \end{align*} $$
$$ \begin{align*}\mathrm{cloud}(L) : = \bigcup_{M = (G,f) \textrm{ min. membr. with bound. }L } \{f(v)\mid v \textrm{ is vertex of } G\}. \end{align*} $$
Remark 28.2. According to Corollary 26.7, for a polypositroid loop
![]() $L=L_P$
,
$L=L_P$
,
![]() $\mathrm {cloud}(L_P)$
belongs to the set
$\mathrm {cloud}(L_P)$
belongs to the set
![]() $P\cap \mathbb {Z}^n$
of lattice points of the polypositroid P. For some (poly)positroids,
$P\cap \mathbb {Z}^n$
of lattice points of the polypositroid P. For some (poly)positroids,
![]() $\mathrm {cloud}(L_P) = P \cap \mathbb {Z}^n$
. For example, the equality holds if
$\mathrm {cloud}(L_P) = P \cap \mathbb {Z}^n$
. For example, the equality holds if
![]() $P = P_{\mathcal {M}}$
, where
$P = P_{\mathcal {M}}$
, where
![]() ${\mathcal {M}} = \binom {[n]}{k}$
is the uniform matroid. In this case, P is the hypersimplex
${\mathcal {M}} = \binom {[n]}{k}$
is the uniform matroid. In this case, P is the hypersimplex
![]() $\Delta (k,n)$
and
$\Delta (k,n)$
and
![]() $\mathrm {cloud}(L_P)=\{e_I \mid I\in {[n]\choose k}\}$
is the set of all lattice points of
$\mathrm {cloud}(L_P)=\{e_I \mid I\in {[n]\choose k}\}$
is the set of all lattice points of
![]() $\Delta (k,n)$
.
$\Delta (k,n)$
.
However, in general,
![]() $\mathrm {cloud}(L_P)$
is not equal to
$\mathrm {cloud}(L_P)$
is not equal to
![]() $P\cap \mathbb {Z}^n$
. For example, if the loop L is a wedge of line segments, then any minimal membrane with boundary L has no triangles. In this case,
$P\cap \mathbb {Z}^n$
. For example, if the loop L is a wedge of line segments, then any minimal membrane with boundary L has no triangles. In this case,
![]() $\mathrm {cloud}(L)=L$
. Apart from some trivial cases, this set cannot be equal to the set of lattice points of the polypositroid P, which is a convex polytope.
$\mathrm {cloud}(L)=L$
. Apart from some trivial cases, this set cannot be equal to the set of lattice points of the polypositroid P, which is a convex polytope.
For the case
![]() $n=3$
, a generic polypositroid is a hexagon, and the associated cloud is a triangle with line segments attached to its vertices.
$n=3$
, a generic polypositroid is a hexagon, and the associated cloud is a triangle with line segments attached to its vertices.
Definition 28.3. For a loop L, let
![]() $\mathrm {Octa}_L:=\mathbb {C}[x_{\lambda },x_{\mu }^{-1}]_{\lambda \in \mathrm {cloud}(L),\mu \in L}$
be the commutative algebra over
$\mathrm {Octa}_L:=\mathbb {C}[x_{\lambda },x_{\mu }^{-1}]_{\lambda \in \mathrm {cloud}(L),\mu \in L}$
be the commutative algebra over
![]() $\mathbb {C}$
generated by the variables
$\mathbb {C}$
generated by the variables
![]() $x_{\lambda }$
, for
$x_{\lambda }$
, for
![]() $\lambda \in \mathrm {cloud}(L)$
, and
$\lambda \in \mathrm {cloud}(L)$
, and
![]() $x_{\mu }^{-1}$
for
$x_{\mu }^{-1}$
for
![]() $\mu \in L$
, modulo the octahedron relations (28.1). We call
$\mu \in L$
, modulo the octahedron relations (28.1). We call
![]() $\mathrm {Octa}_L$
the octahedron algebra of the loop L.
$\mathrm {Octa}_L$
the octahedron algebra of the loop L.
Recall that, for any finite quiver (i.e., a directed graph) Q with a chosen subset of vertices B, there is a cluster algebra, whose initial cluster variables correspond to vertices of Q and frozen cluster variables correspond to the subset of vertices B (see [Reference Fomin and ZelevinskyFZ02]). By convention, we will assume that the inverses of frozen cluster variables belong to the cluster algebra.
Definition 28.4. For a membrane
![]() $M=(G,f)$
, define the quiver of M as the directed graph
$M=(G,f)$
, define the quiver of M as the directed graph
![]() $Q(M)$
on the same set of vertices
$Q(M)$
on the same set of vertices
![]() ${\mathrm {Vert}}$
as the cactus G, whose edges
${\mathrm {Vert}}$
as the cactus G, whose edges
![]() $u\to v$
are the edges of G that separate triangles of different colors, directed so that the adjacent black triangle is on the right of the edge
$u\to v$
are the edges of G that separate triangles of different colors, directed so that the adjacent black triangle is on the right of the edge
![]() $u\to v$
and the adjacent white triangle is on the left of the edge
$u\to v$
and the adjacent white triangle is on the left of the edge
![]() $u\to v$
.
$u\to v$
.
Let
![]() ${\mathcal {A}}_M$
denote the cluster algebra over
${\mathcal {A}}_M$
denote the cluster algebra over
![]() $\mathbb {C}$
given by the quiver
$\mathbb {C}$
given by the quiver
![]() $Q(M)$
of the membrane M with frozen variables corresponding to the boundary vertices
$Q(M)$
of the membrane M with frozen variables corresponding to the boundary vertices
![]() $b_i\in {\mathrm {Vert}}$
of G.
$b_i\in {\mathrm {Vert}}$
of G.
Theorem 28.5. Let L be any j-increasing loop (in particular, L can be any polypositroid loop). Let
![]() $M=(G,f)$
be any minimal membrane with boundary loop L, and let
$M=(G,f)$
be any minimal membrane with boundary loop L, and let
![]() ${\mathrm {Vert}}$
be the vertex set G.
${\mathrm {Vert}}$
be the vertex set G.
For any other minimal membrane
![]() $M'$
with the same boundary loop L, the quivers
$M'$
with the same boundary loop L, the quivers
![]() $Q(M)$
and
$Q(M)$
and
![]() $Q(M')$
are mutation equivalent, and we have a canonical isomorphism
$Q(M')$
are mutation equivalent, and we have a canonical isomorphism
![]() ${\mathcal {A}}_{M}\simeq {\mathcal {A}}_{M'}$
. The octahedron algebra
${\mathcal {A}}_{M}\simeq {\mathcal {A}}_{M'}$
. The octahedron algebra
![]() $\mathrm {Octa}_L$
is a (finitely generated) subalgebra of the cluster algebra
$\mathrm {Octa}_L$
is a (finitely generated) subalgebra of the cluster algebra
![]() ${\mathcal {A}}_M$
.
${\mathcal {A}}_M$
.
More explicitly, let us identify the collection of variables
![]() $\{x_{f(v)}\mid v \in {\mathrm {Vert}}\}$
with the initial cluster of
$\{x_{f(v)}\mid v \in {\mathrm {Vert}}\}$
with the initial cluster of
![]() ${\mathcal {A}}_M$
. We have
${\mathcal {A}}_M$
. We have
-
1. The collection of variables
 $\{x_{f(v)}\mid v\in {\mathrm {Vert}}\}$
is an algebraically independent set in
$\{x_{f(v)}\mid v\in {\mathrm {Vert}}\}$
is an algebraically independent set in
 $\mathrm {Octa}_L$
. Any other
$\mathrm {Octa}_L$
. Any other
 $x_{\lambda }$
, for
$x_{\lambda }$
, for
 $\lambda \in \mathrm {cloud}(L)$
is expressed in terms of these variables by Laurent polynomials with positive integer coefficients.
$\lambda \in \mathrm {cloud}(L)$
is expressed in terms of these variables by Laurent polynomials with positive integer coefficients. -
2. Local moves of membranes of types (I) and (III) (tetrahedron moves) do not change the set of variables
 $\{x_{f(v)}\mid v\in {\mathrm {Vert}}\}$
, and they do not change the quiver
$\{x_{f(v)}\mid v\in {\mathrm {Vert}}\}$
, and they do not change the quiver
 $Q(M)$
of M and the cluster algebra
$Q(M)$
of M and the cluster algebra
 ${\mathcal {A}}_M$
.
${\mathcal {A}}_M$
. -
3. Local moves of membranes of type (II) (octahedron moves) change exactly one element in the set
 $\{x_{f(v)}\mid v\in {\mathrm {Vert}}\}$
. They correspond to (a certain class of) mutations of the cluster algebra
$\{x_{f(v)}\mid v\in {\mathrm {Vert}}\}$
. They correspond to (a certain class of) mutations of the cluster algebra
 ${\mathcal {A}}_M$
.
${\mathcal {A}}_M$
. -
4. Any minimal membrane
 $M'=(G',f')$
with the same boundary loop L is obtained from M by a sequence of local moves. The collection of variables
$M'=(G',f')$
with the same boundary loop L is obtained from M by a sequence of local moves. The collection of variables
 $\{x_{f'(v')}\mid v'\in {\mathrm {Vert}}'\}$
(where
$\{x_{f'(v')}\mid v'\in {\mathrm {Vert}}'\}$
(where
 ${\mathrm {Vert}}'$
is the set of vertices of
${\mathrm {Vert}}'$
is the set of vertices of
 $G'$
) is a cluster of the cluster algebra
$G'$
) is a cluster of the cluster algebra
 ${\mathcal {A}}_M$
.
${\mathcal {A}}_M$
. -
5. The isomorphism
 $\mu _{M,M'}:{\mathcal {A}}_M\to {\mathcal {A}}_M'$
given by the composition of mutations coming from a sequence of local moves connecting the membranes M and
$\mu _{M,M'}:{\mathcal {A}}_M\to {\mathcal {A}}_M'$
given by the composition of mutations coming from a sequence of local moves connecting the membranes M and
 $M'$
depends only on the membranes M and
$M'$
depends only on the membranes M and
 $M'$
, and it does not depend on a choice of a sequence of local moves connecting the membranes.
$M'$
, and it does not depend on a choice of a sequence of local moves connecting the membranes. -
6. The octahedron algebra
 $\mathrm {Octa}_L$
is the subalgebra of the cluster algebra
$\mathrm {Octa}_L$
is the subalgebra of the cluster algebra
 ${\mathcal {A}}_M$
generated by all cluster variables from all clusters of
${\mathcal {A}}_M$
generated by all cluster variables from all clusters of
 ${\mathcal {A}}_M$
(and inverses of frozen variables) that correspond to minimal membranes
${\mathcal {A}}_M$
(and inverses of frozen variables) that correspond to minimal membranes
 $M'$
with the same boundary loop L.
$M'$
with the same boundary loop L.
Proof. Part (2) is clear, because tetrahedron moves of membranes do not change the set of points
![]() $\{f(v)\mid v\in {\mathrm {Vert}}\}$
, and they do not change the quiver Q of a membrane.
$\{f(v)\mid v\in {\mathrm {Vert}}\}$
, and they do not change the quiver Q of a membrane.
Observe that, if we apply a move
![]() $M\to \tilde M$
of type (II) (an octahedron move), that is, apply a square move of the associated plabic graph
$M\to \tilde M$
of type (II) (an octahedron move), that is, apply a square move of the associated plabic graph
![]() $G^*$
, then the labels
$G^*$
, then the labels
![]() $i,j,k,l$
of the four strands (arranged clockwise) going out of the vertices of the square are ordered as
$i,j,k,l$
of the four strands (arranged clockwise) going out of the vertices of the square are ordered as
![]() $i<j<k<l$
(up to a cyclic shift) (see the argument in the proof of Theorem 27.4). One easily checks that the quiver
$i<j<k<l$
(up to a cyclic shift) (see the argument in the proof of Theorem 27.4). One easily checks that the quiver
![]() $Q(\tilde M)$
is a mutation of the quiver
$Q(\tilde M)$
is a mutation of the quiver
![]() $Q(M)$
. This move results in replacing one element
$Q(M)$
. This move results in replacing one element
![]() $x_{e_i + e_k + \lambda }$
of the set
$x_{e_i + e_k + \lambda }$
of the set
![]() $\{x_{f(v)}\mid v\in {\mathrm {Vert}}\}$
by
$\{x_{f(v)}\mid v\in {\mathrm {Vert}}\}$
by
![]() $x_{e_j+e_l+\lambda }$
. One checks from the definitions that the transformation:
$x_{e_j+e_l+\lambda }$
. One checks from the definitions that the transformation:
is exactly the cluster mutation of the associated variable in the initial cluster of
![]() ${\mathcal {A}}_M$
. So we get part (3).
${\mathcal {A}}_M$
. So we get part (3).
Part (4) follows from Theorem 23.6 and the fact the that loop L is unimodal.
Part (1) now follows from general results on cluster algebras, namely, Fomin-Zelevinsky’s Laurent phenomenon [Reference Fomin and ZelevinskyFZ03] and the positivity result of Lee-Schiffler [Reference Lee and SchifflerLS].
Part (5) follows from the observation that each element of the initial seed of the cluster algebra
![]() ${\mathcal {A}}_{M'}$
corresponds to some variable
${\mathcal {A}}_{M'}$
corresponds to some variable
![]() $x_{f'(v')}$
,
$x_{f'(v')}$
,
![]() $v'\in {\mathrm {Vert}}'$
. By part (1), this element is expressed by a Laurent polynomial in terms of the variables
$v'\in {\mathrm {Vert}}'$
. By part (1), this element is expressed by a Laurent polynomial in terms of the variables
![]() $x_{f(v)}$
,
$x_{f(v)}$
,
![]() $v\in {\mathrm {Vert}}$
, corresponding to the initial seed of
$v\in {\mathrm {Vert}}$
, corresponding to the initial seed of
![]() ${\mathcal {A}}_M$
. This Laurent expression depends only on the membrane M and the integer vector
${\mathcal {A}}_M$
. This Laurent expression depends only on the membrane M and the integer vector
![]() $f'(v')\in \mathbb {Z}^n$
, and it does not depend on a choice of a sequence of local moves connecting the membranes M and
$f'(v')\in \mathbb {Z}^n$
, and it does not depend on a choice of a sequence of local moves connecting the membranes M and
![]() $M'$
.
$M'$
.
Part (6) is clear from the above discussion.
For a j-increasing loop L, we denote by
![]() ${\mathcal {A}}_L$
the cluster algebra
${\mathcal {A}}_L$
the cluster algebra
![]() ${\mathcal {A}}_M$
for a minimal membrane M with boundary loop L. The quiver
${\mathcal {A}}_M$
for a minimal membrane M with boundary loop L. The quiver
![]() $Q(M)$
, and thus the cluster algebra
$Q(M)$
, and thus the cluster algebra
![]() ${\mathcal {A}}_M$
, of a minimal membrane
${\mathcal {A}}_M$
, of a minimal membrane
![]() $M=(G,f)$
depends only on the reduced plabic graph
$M=(G,f)$
depends only on the reduced plabic graph
![]() $G^*$
. Since every reduced plabic graph appears in a minimal positroid membrane, the class of cluster algebras
$G^*$
. Since every reduced plabic graph appears in a minimal positroid membrane, the class of cluster algebras
![]() ${\mathcal {A}}_L$
is as general as its subclass corresponding to positroid loops. However, the description of these cluster algebras in terms of the higher octahedron recurrence allows us to associate some cluster variables with points of the integer lattice
${\mathcal {A}}_L$
is as general as its subclass corresponding to positroid loops. However, the description of these cluster algebras in terms of the higher octahedron recurrence allows us to associate some cluster variables with points of the integer lattice
![]() $\mathbb {Z}^n$
and some clusters with membranes, which provides an additional geometrical intuition into the structure of these cluster algebras.
$\mathbb {Z}^n$
and some clusters with membranes, which provides an additional geometrical intuition into the structure of these cluster algebras.
Let
![]() ${\mathcal {M}}$
be a positroid, and let
${\mathcal {M}}$
be a positroid, and let
![]() ${\mathcal {A}}_{L_{\mathcal {M}}}$
be the cluster algebra for the positroid loop
${\mathcal {A}}_{L_{\mathcal {M}}}$
be the cluster algebra for the positroid loop
![]() $L_{\mathcal {M}}$
(see Section 24). The cluster algebra
$L_{\mathcal {M}}$
(see Section 24). The cluster algebra
![]() ${\mathcal {A}}_{L_{\mathcal {M}}}$
implicitly appeared in [Reference PostnikovPo06]. It was shown in [Reference Galashin and LamGL] that the cluster algebra
${\mathcal {A}}_{L_{\mathcal {M}}}$
implicitly appeared in [Reference PostnikovPo06]. It was shown in [Reference Galashin and LamGL] that the cluster algebra
![]() ${\mathcal {A}}_{L_{\mathcal {M}}}$
is isomorphic to the coordinate ring
${\mathcal {A}}_{L_{\mathcal {M}}}$
is isomorphic to the coordinate ring
![]() $\mathbb {C}[\mathring \Pi _{\mathcal {M}}]$
of an open positroid variety
$\mathbb {C}[\mathring \Pi _{\mathcal {M}}]$
of an open positroid variety
![]() $\mathring \Pi _{\mathcal {M}}$
[Reference Knutson, Lam and SpeyerKLS], confirming conjectures of Muller–Speyer [Reference Muller and SpeyerMS] and Leclerc [Reference LeclercLec].
$\mathring \Pi _{\mathcal {M}}$
[Reference Knutson, Lam and SpeyerKLS], confirming conjectures of Muller–Speyer [Reference Muller and SpeyerMS] and Leclerc [Reference LeclercLec].
Remark 28.6. Suppose that
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are two j-increasing loops, and
$L_2$
are two j-increasing loops, and
![]() $M_1=(G_1,f_1)$
and
$M_1=(G_1,f_1)$
and
![]() $M_2=(G_2,f_2)$
are minimal membranes with boundary loops
$M_2=(G_2,f_2)$
are minimal membranes with boundary loops
![]() $L_1$
and
$L_1$
and
![]() $L_2$
, respectively. If the reduced plabic graphs
$L_2$
, respectively. If the reduced plabic graphs
![]() $G_1^*$
and
$G_1^*$
and
![]() $G_2^*$
are connected by the local moves (I), (II), and (III), then it follows from the above remarks that
$G_2^*$
are connected by the local moves (I), (II), and (III), then it follows from the above remarks that
![]() $\mathrm {cloud}(L_1)$
and
$\mathrm {cloud}(L_1)$
and
![]() $\mathrm {cloud}(L_2)$
are naturally in bijection.
$\mathrm {cloud}(L_2)$
are naturally in bijection.
Remark 28.7. The cluster algebra
![]() ${\mathcal {A}}_L$
is typically a cluster algebra of infinite type, with infinitely many cluster variables. On the other hand,
${\mathcal {A}}_L$
is typically a cluster algebra of infinite type, with infinitely many cluster variables. On the other hand,
![]() $\mathrm {cloud}(L)$
is a finite set, corresponding to a finite subset of the cluster variables of
$\mathrm {cloud}(L)$
is a finite set, corresponding to a finite subset of the cluster variables of
![]() ${\mathcal {A}}_L$
, and thus the octahedron algebra
${\mathcal {A}}_L$
, and thus the octahedron algebra
![]() $\mathrm {Octa}_L$
is a finitely generated subalgebra of the cluster algebra
$\mathrm {Octa}_L$
is a finitely generated subalgebra of the cluster algebra
![]() ${\mathcal {A}}_L$
. However, even when
${\mathcal {A}}_L$
. However, even when
![]() ${\mathcal {A}}_L$
is of infinite type, we may have
${\mathcal {A}}_L$
is of infinite type, we may have
![]() $\mathrm {Octa}_L = {\mathcal {A}}_L$
. For example, this holds when the reduced plabic graph
$\mathrm {Octa}_L = {\mathcal {A}}_L$
. For example, this holds when the reduced plabic graph
![]() $G^*$
corresponds to the top positroid cell of
$G^*$
corresponds to the top positroid cell of
![]() $\mathrm {Gr}(k,n)$
. In this case,
$\mathrm {Gr}(k,n)$
. In this case,
![]() ${\mathcal {A}}_L$
is isomorphic to the homogeneous coordinate ring of the Grassmannian with the cyclic minors
${\mathcal {A}}_L$
is isomorphic to the homogeneous coordinate ring of the Grassmannian with the cyclic minors
![]() $\Delta _{12\cdots k}, \Delta _{23 \cdots (k+1)},\ldots $
inverted. The equality
$\Delta _{12\cdots k}, \Delta _{23 \cdots (k+1)},\ldots $
inverted. The equality
![]() $\mathrm {Octa}_L={\mathcal {A}}_L$
follows from the fact that the homogeneous coordinate ring of the Grassmannian is generated by Plücker coordinates
$\mathrm {Octa}_L={\mathcal {A}}_L$
follows from the fact that the homogeneous coordinate ring of the Grassmannian is generated by Plücker coordinates
![]() $\Delta _I$
.
$\Delta _I$
.
29. Asymptotic cluster algebra
As we discussed in Section 28, membranes are closely related to a class of cluster algebras generated by some collections of variables satisfying the higher octahedron recurrence. Minimal membranes correspond to certain clusters in these algebras, and local moves of membranes correspond to cluster mutations. It would be interesting to investigate the asymptotic behavior of these structures under dilations of the boundary loop.
We can call this area of research the “Asymptotic Cluster Algebra.” We anticipate that many results from statistical physics and from asymptotic representation theory (e.g., the study of asymptotics properties of representations of symmetric groups), will have their analogs in the asymptotic cluster algebra.
Under dilations of the boundary loop L, minimal membranes might approach a certain limit surface S.
Let
![]() $\mathrm {Memb}(L)$
be the set of all minimal membranes with boundary loop L. For
$\mathrm {Memb}(L)$
be the set of all minimal membranes with boundary loop L. For
![]() $t\in \mathbb {Z}_{>0}$
, let
$t\in \mathbb {Z}_{>0}$
, let
![]() $tL$
denote the loop L dilated t times.
$tL$
denote the loop L dilated t times.
Conjecture 29.1. Let L be a unimodal loop. For a positive integer t, consider the uniform distribution on the set
![]() $\mathrm {Memb}(tL)$
.
$\mathrm {Memb}(tL)$
.
There exists a unique surface
![]() $S\subset \mathbb {R}^n$
(with boundary
$S\subset \mathbb {R}^n$
(with boundary
![]() $\left <L\right>$
), such that, for any
$\left <L\right>$
), such that, for any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $N>0$
, such that, for any
$N>0$
, such that, for any
![]() $t\geq N$
, the probability that
$t\geq N$
, the probability that
![]() ${1\over t} \left <M\right>$
, for
${1\over t} \left <M\right>$
, for
![]() $M\in \mathrm {Memb}(tL)$
, belongs to the
$M\in \mathrm {Memb}(tL)$
, belongs to the
![]() $\epsilon $
-neighborhood of S is greater than
$\epsilon $
-neighborhood of S is greater than
![]() $1-\epsilon $
.
$1-\epsilon $
.
A related conjecture can be formulated in terms of measures. For a loop L, consider the measure
![]() $\mu _L$
on the set
$\mu _L$
on the set
![]() $\mathrm {cloud}(L)\subset \mathbb {Z}^n$
given by
$\mathrm {cloud}(L)\subset \mathbb {Z}^n$
given by
for
![]() $a\in \mathbb {Z}^n$
. Clearly,
$a\in \mathbb {Z}^n$
. Clearly,
![]() $\sum _{a\in \mathbb {Z}^n} \mu _L(a) = 1$
, so
$\sum _{a\in \mathbb {Z}^n} \mu _L(a) = 1$
, so
![]() $\mu _L$
is a probability distribution.
$\mu _L$
is a probability distribution.
Equivalently,
![]() $\mu _L(a)$
is the probability that a random (uniformly chosen) minimal membrane with boundary L contains a lattice point a. In other words,
$\mu _L(a)$
is the probability that a random (uniformly chosen) minimal membrane with boundary L contains a lattice point a. In other words,
![]() $\mu _L$
is the density of a random membrane.
$\mu _L$
is the density of a random membrane.
For a positive integer t, let
![]() $\mu _{L,t}(a) := \mu _{tL}(ta)$
. The measure (probability distribution)
$\mu _{L,t}(a) := \mu _{tL}(ta)$
. The measure (probability distribution)
![]() $\mu _{L,t}$
is supported on a certain subset of the lattice
$\mu _{L,t}$
is supported on a certain subset of the lattice
![]() $({1\over t} \mathbb {Z})^n$
.
$({1\over t} \mathbb {Z})^n$
.
Conjecture 29.2. Let L be a unimodular loop. As
![]() $t\to \infty $
, the measures
$t\to \infty $
, the measures
![]() $\mu _{L,t}$
converge to a certain limit measure
$\mu _{L,t}$
converge to a certain limit measure
supported on a certain limit surface
![]() $S\subset \mathbb {R}^n$
.
$S\subset \mathbb {R}^n$
.
Remark 29.3. For
![]() $n=4$
, semisimple membranes are related to the 6-vertex and 8-vertex models [Reference BaxterBax], whose asymptotic properties have been extensively studied.
$n=4$
, semisimple membranes are related to the 6-vertex and 8-vertex models [Reference BaxterBax], whose asymptotic properties have been extensively studied.
Remark 29.4. It would be interesting to investigate a relationship between the “limit membrane” S and Plateau’s problem (see Remark 20.7).
Acknowledgements
We thank Michael Joswig for helpful comments on an earlier draft, and the referee for a number of corrections. T.L. was supported by NSF DMS-0600677, DMS-0652641, DMS-0901111, DMS-0968696, DMS-1160726, DMS-1464693, and DMS-1953852. A.P. was supported by NSF DMS-0546209, DMS-1100147, DMS-1362336, DMS-1500219, and DMS-1764370.
Competing interest
The authors have no competing interest to declare.