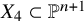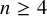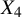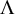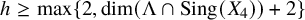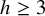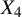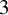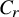1 Introduction
An n-dimensional variety X over a field k is rational if it is birational to
![]() $\mathbb {P}^n_{k}$
, while X is unirational if there is a dominant rational map
$\mathbb {P}^n_{k}$
, while X is unirational if there is a dominant rational map
![]() . If k is infinite and X is unirational, then the set
. If k is infinite and X is unirational, then the set
![]() $X(k)$
of the k-rational points of X is Zariski dense in X.
$X(k)$
of the k-rational points of X is Zariski dense in X.
Since the first half of the twentieth century, the problem of establishing whether a degree d hypersurface
![]() $X_d\subset \mathbb {P}^{n+1}$
is rational or unirational has been central in birational projective geometry [Reference MorinMor42], [Reference PredonzanPre49], [Reference MorinMor52], [Reference Iskovskih and ManinIM71], [Reference Clemens and GriffithsCG72], [Reference CilibertoCil80], [Reference KollárKol95], [Reference ShimadaShi95], [Reference Harris, Mazur and PandharipandeHMP98], [Reference Harris and TschinkelHT00], [Reference de FernexdF13], [Reference Bolognesi, Russo and StaglianòBRS19], [Reference Russo and StaglianòRS19].
$X_d\subset \mathbb {P}^{n+1}$
is rational or unirational has been central in birational projective geometry [Reference MorinMor42], [Reference PredonzanPre49], [Reference MorinMor52], [Reference Iskovskih and ManinIM71], [Reference Clemens and GriffithsCG72], [Reference CilibertoCil80], [Reference KollárKol95], [Reference ShimadaShi95], [Reference Harris, Mazur and PandharipandeHMP98], [Reference Harris and TschinkelHT00], [Reference de FernexdF13], [Reference Bolognesi, Russo and StaglianòBRS19], [Reference Russo and StaglianòRS19].
Quadric hypersurfaces with a smooth point are rational and as proven by J. Kollár, building on techniques of B. Segre [Reference SegreSeg43] and Y. I. Manin [Reference Manin and FormsMan86, Chapter 2, Section 12], cubic hypersurfaces with a smooth point are unirational [Reference KollárKol02]. U. Morin proved that a general complex hypersurface
![]() $X_d\subset \mathbb {P}^{n+1}$
is unirational provided that n is large enough with respect to d [Reference MorinMor42]. This result has then been reproved, in a different way, by C. Ciliberto [Reference CilibertoCil80] and extended to complete intersections by A. Predonzan [Reference PredonzanPre49], K. Paranjape, V. Srinivas [Reference Paranjape and SrinivasPS92] and L. Ramero [Reference RameroRam90].
$X_d\subset \mathbb {P}^{n+1}$
is unirational provided that n is large enough with respect to d [Reference MorinMor42]. This result has then been reproved, in a different way, by C. Ciliberto [Reference CilibertoCil80] and extended to complete intersections by A. Predonzan [Reference PredonzanPre49], K. Paranjape, V. Srinivas [Reference Paranjape and SrinivasPS92] and L. Ramero [Reference RameroRam90].
Furthermore, J. Harris, B. Mazur and R. Pandharipande proved that
![]() $X_d\subset \mathbb {P}^{n+1}$
is unirational if the codimension of its singular locus is sufficiently big with respect to n and d [Reference Harris, Mazur and PandharipandeHMP98].
$X_d\subset \mathbb {P}^{n+1}$
is unirational if the codimension of its singular locus is sufficiently big with respect to n and d [Reference Harris, Mazur and PandharipandeHMP98].
Before stating our main results on the unirationality of quartics we briefly survey the state of the art. By the work of U. Morin, a general complex quartic
![]() $X_4\subset \mathbb {P}^{n+1}$
with
$X_4\subset \mathbb {P}^{n+1}$
with
![]() $n\geq 5$
is unirational [Reference MorinMor36], [Reference MorinMor52]. V. A. Iskovskikh and Y. I. Manin proved that the group of the birational automorphisms of a smooth quartic
$n\geq 5$
is unirational [Reference MorinMor36], [Reference MorinMor52]. V. A. Iskovskikh and Y. I. Manin proved that the group of the birational automorphisms of a smooth quartic
![]() $X_4\subset \mathbb {P}^4$
is finite so that
$X_4\subset \mathbb {P}^4$
is finite so that
![]() $X_4$
is not rational [Reference Iskovskih and ManinIM71].
$X_4$
is not rational [Reference Iskovskih and ManinIM71].
Moreover, J. Harris and Y. Tschinkel showed that if
![]() $n\geq 3$
and k is a number field, then for some finite extension
$n\geq 3$
and k is a number field, then for some finite extension
![]() $k'$
of k the set of
$k'$
of k the set of
![]() $k'$
-rational points of a smooth quartic
$k'$
-rational points of a smooth quartic
![]() $X_4\subset \mathbb {P}^{n+1}$
is dense in the Zariski topology; in other terms, the k-rational points of
$X_4\subset \mathbb {P}^{n+1}$
is dense in the Zariski topology; in other terms, the k-rational points of
![]() $X_4$
are potentially dense [Reference Harris and TschinkelHT00]. Despite this great amount of effort, the unirationality of the general quartic
$X_4$
are potentially dense [Reference Harris and TschinkelHT00]. Despite this great amount of effort, the unirationality of the general quartic
![]() $X_4\subset \mathbb {P}^n$
for
$X_4\subset \mathbb {P}^n$
for
![]() $n = 4,5$
is still an open problem and only special families of quartic
$n = 4,5$
is still an open problem and only special families of quartic
![]() $3$
-folds, called quartics with separable asymptotics, are known to be unirational [Reference SegreSeg60]. For a nice survey on rationality and unirationality problems with a focus on their relation with the notion of rational connection, we refer to A. Verra’s paper [Reference VerraVer08]. We recall that a projective variety is rationally connected if any two of its points can be joined by a rational curve and refer to C. Araujo’s paper [Reference AraujoAra05] for a survey on the subject.
$3$
-folds, called quartics with separable asymptotics, are known to be unirational [Reference SegreSeg60]. For a nice survey on rationality and unirationality problems with a focus on their relation with the notion of rational connection, we refer to A. Verra’s paper [Reference VerraVer08]. We recall that a projective variety is rationally connected if any two of its points can be joined by a rational curve and refer to C. Araujo’s paper [Reference AraujoAra05] for a survey on the subject.
In this paper, we address the unirationality of quartics
![]() $X_4\subset \mathbb {P}^{n+1}$
containing a linear subspace whose dimension is larger than that of the singular locus of
$X_4\subset \mathbb {P}^{n+1}$
containing a linear subspace whose dimension is larger than that of the singular locus of
![]() $X_4$
or containing a linear subspace with multiplicity two. Our main results in Theorems 3.15 and 3.22 can be summarized as follows:
$X_4$
or containing a linear subspace with multiplicity two. Our main results in Theorems 3.15 and 3.22 can be summarized as follows:
Theorem 1.1. Let
![]() $X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface and
$X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface and
![]() $\Lambda \subset \mathbb {P}^{n+1}$
an h-plane. Assume that either
$\Lambda \subset \mathbb {P}^{n+1}$
an h-plane. Assume that either
-
(i)
 $n\geq 3, h\geq 2$
,
$n\geq 3, h\geq 2$
,
 $\dim (\Lambda \cap \operatorname {\mathrm {Sing}}(X_4))\leq h-2$
,
$\dim (\Lambda \cap \operatorname {\mathrm {Sing}}(X_4))\leq h-2$
,
 $X_4$
contains
$X_4$
contains
 $\Lambda $
and is not a cone over a smaller-dimensional quartic, or
$\Lambda $
and is not a cone over a smaller-dimensional quartic, or -
(ii)
 $n\geq 4, h\geq 3$
,
$n\geq 4, h\geq 3$
,
 $X_4$
has double points along
$X_4$
has double points along
 $\Lambda $
, a point
$\Lambda $
, a point
 $p\in X_4\setminus \Lambda $
and is otherwise general,
$p\in X_4\setminus \Lambda $
and is otherwise general,
then
![]() $X_4$
is unirational.
$X_4$
is unirational.
All along the paper with the word ‘general’ we mean ‘for a nonempty Zariski open subset of the parameter space of the objects we are considering’. We would like to stress that since all the proofs presented in the paper are constructive it is possible, given the equation cutting out the hypersurface, to establish whether or not it is general in the required sense.
Furthermore, for quartic
![]() $3$
-folds over a number field we prove, in Proposition 3.14, the following density result.
$3$
-folds over a number field we prove, in Proposition 3.14, the following density result.
Theorem 1.2. Let
![]() $X_4\subset \mathbb {P}^{4}$
be a quartic hypersurface, over a number field k, having double points along a codimension two linear subspace
$X_4\subset \mathbb {P}^{4}$
be a quartic hypersurface, over a number field k, having double points along a codimension two linear subspace
![]() $\Lambda \subset \mathbb {P}^{4}$
, with a point
$\Lambda \subset \mathbb {P}^{4}$
, with a point
![]() $p\in X_4\setminus \Lambda $
and otherwise general. The set
$p\in X_4\setminus \Lambda $
and otherwise general. The set
![]() $X_4(k)$
of the k-rational points of
$X_4(k)$
of the k-rational points of
![]() $X_4$
is Zariski dense in
$X_4$
is Zariski dense in
![]() $X_4$
.
$X_4$
.
As Remark 3.17 shows, the assumption on the existence of a point
![]() $p\in X_4\setminus \Lambda $
in the case of quartics singular along a linear subspace cannot be dropped. Under extra assumptions on the base field or on the existence of rational points in special subloci of
$p\in X_4\setminus \Lambda $
in the case of quartics singular along a linear subspace cannot be dropped. Under extra assumptions on the base field or on the existence of rational points in special subloci of
![]() $X_4$
, Theorem 1.1 can be extended to smaller-dimensional quartics. For instance, by Proposition 3.19 a quartic surface
$X_4$
, Theorem 1.1 can be extended to smaller-dimensional quartics. For instance, by Proposition 3.19 a quartic surface
![]() $X_4\subset \mathbb {P}^3$
with double points along a line
$X_4\subset \mathbb {P}^3$
with double points along a line
![]() $\Lambda \subset \mathbb {P}^3$
, a point
$\Lambda \subset \mathbb {P}^3$
, a point
![]() $p\in X_4\setminus \Lambda $
, a double point
$p\in X_4\setminus \Lambda $
, a double point
![]() $q\in X_4\setminus \Lambda $
with
$q\in X_4\setminus \Lambda $
with
![]() $q\neq p$
and otherwise general is unirational. Furthermore, by the second part of Theorem 3.15 a quartic
$q\neq p$
and otherwise general is unirational. Furthermore, by the second part of Theorem 3.15 a quartic
![]() $X_4\subset \mathbb {P}^{4}$
over a
$X_4\subset \mathbb {P}^{4}$
over a
![]() $C_r$
field, for which definition we refer to Remark 2.10, with
$C_r$
field, for which definition we refer to Remark 2.10, with
![]() $r = 0,1$
, having double points along a linear subspace
$r = 0,1$
, having double points along a linear subspace
![]() $\Lambda $
with
$\Lambda $
with
![]() $\dim (\Lambda ) = 1,2$
, and otherwise general is unirational. Therefore, in order to complete Theorem 1.1 for all n and h we are left with the following open question.
$\dim (\Lambda ) = 1,2$
, and otherwise general is unirational. Therefore, in order to complete Theorem 1.1 for all n and h we are left with the following open question.
Question 1.3. Let
![]() $X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface over a field k such that either
$X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface over a field k such that either
-
(i)
 $n = 3$
,
$n = 3$
,
 $X_4$
contains a line, or
$X_4$
contains a line, or -
(ii)
 $n = 3$
,
$n = 3$
,
 $X_4$
has double points along a linear subspace
$X_4$
has double points along a linear subspace
 $\Lambda $
with
$\Lambda $
with
 $\dim (\Lambda ) = 1,2$
, a point
$\dim (\Lambda ) = 1,2$
, a point
 $p\in X_4\setminus \Lambda $
, or
$p\in X_4\setminus \Lambda $
, or -
(iii)
 $n = 2$
,
$n = 2$
,
 $X_4$
has double points along a line
$X_4$
has double points along a line
 $\Lambda $
, a point
$\Lambda $
, a point
 $p\in X_4\setminus \Lambda $
,
$p\in X_4\setminus \Lambda $
,
and
![]() $X_4$
is otherwise general. Is then
$X_4$
is otherwise general. Is then
![]() $X_4$
unirational?
$X_4$
unirational?
Note that a smooth quartic surface
![]() $X_4\subset \mathbb {P}^3$
is
$X_4\subset \mathbb {P}^3$
is
![]() $K3$
, and hence, it cannot be unirational. As we said,
$K3$
, and hence, it cannot be unirational. As we said,
![]() $\text {(ii)}$
has a positive answer when the base field is
$\text {(ii)}$
has a positive answer when the base field is
![]() $C_r$
with
$C_r$
with
![]() $r = 0,1$
, while
$r = 0,1$
, while
![]() $\text {(i)}$
is open even over the complex numbers. Since any complex quartic
$\text {(i)}$
is open even over the complex numbers. Since any complex quartic
![]() $3$
-fold contains a line,
$3$
-fold contains a line,
![]() $\text {(i)}$
actually asks about the unirationality of a general quartic
$\text {(i)}$
actually asks about the unirationality of a general quartic
![]() $3$
-fold and is probably one of the most interesting unirationality open problems. Since a quartic surface
$3$
-fold and is probably one of the most interesting unirationality open problems. Since a quartic surface
![]() $X_4\subset \mathbb {P}^3$
with a double line is birational to a conic bundle,
$X_4\subset \mathbb {P}^3$
with a double line is birational to a conic bundle,
![]() $\text {(iii)}$
is interesting only when the base field is not algebraically closed.
$\text {(iii)}$
is interesting only when the base field is not algebraically closed.
Note that by considering the generic fiber of the resolution of the linear projection from
![]() $\Lambda $
as in the proof of Theorem 3.15 a positive answer to Question 1.3 would extend the first part of Theorem 1.1 to quartic hypersurfaces
$\Lambda $
as in the proof of Theorem 3.15 a positive answer to Question 1.3 would extend the first part of Theorem 1.1 to quartic hypersurfaces
![]() $X_4\subset \mathbb {P}^{n+1}$
with
$X_4\subset \mathbb {P}^{n+1}$
with
![]() $n\geq 3$
containing a line and the second part of Theorem 1.1 to quartic hypersurfaces
$n\geq 3$
containing a line and the second part of Theorem 1.1 to quartic hypersurfaces
![]() $X_4\subset \mathbb {P}^{n+1}$
with
$X_4\subset \mathbb {P}^{n+1}$
with
![]() $n\geq 3$
having double points along either a line or a plane and an additional smooth point.
$n\geq 3$
having double points along either a line or a plane and an additional smooth point.
Remark 1.4. The main available results in the spirit of Theorem 1.1 can be found in [Reference PredonzanPre49] and [Reference Harris, Mazur and PandharipandeHMP98]. By [Reference PredonzanPre49, Theorem 1] a quartic
![]() $X_4\subset \mathbb {P}^{n+1}$
containing an h-plane
$X_4\subset \mathbb {P}^{n+1}$
containing an h-plane
![]() $\Lambda $
is unirational provided that
$\Lambda $
is unirational provided that
![]() $\operatorname {\mathrm {Sing}}(X_4)\cap \Lambda = \emptyset $
and
$\operatorname {\mathrm {Sing}}(X_4)\cap \Lambda = \emptyset $
and
![]() $h\geq 4$
. The same result has been proved in [Reference Harris, Mazur and PandharipandeHMP98, Corollary 3.7] for
$h\geq 4$
. The same result has been proved in [Reference Harris, Mazur and PandharipandeHMP98, Corollary 3.7] for
![]() $h\geq 97$
.
$h\geq 97$
.
We would like to stress that both [Reference PredonzanPre49] and [Reference Harris, Mazur and PandharipandeHMP98] as well as [Reference RameroRam90] provide unirationality results for hypersurfaces of arbitrary degree and general unirationality bounds when the base field is algebraically closed.
In the case of quartics, Theorem 1.1 (i) improves [Reference PredonzanPre49, Theorem 1] and [Reference Harris, Mazur and PandharipandeHMP98, Corollary 3.7] in two directions: on one side, it is enough to have that
![]() $h\geq 2$
, on the other side,
$h\geq 2$
, on the other side,
![]() $\Lambda $
is allowed to intersect the singular locus of
$\Lambda $
is allowed to intersect the singular locus of
![]() $X_4$
as long as such intersection has codimension at least two in
$X_4$
as long as such intersection has codimension at least two in
![]() $\Lambda $
.
$\Lambda $
.
In the last section, we investigate the unirationality of quintic hypersurfaces and divisors of bidegree
![]() $(3,2)$
in products of projective spaces. As a by-product, we get new examples of unirational but not stably rational varieties.
$(3,2)$
in products of projective spaces. As a by-product, we get new examples of unirational but not stably rational varieties.
A variety X is stably rational if
![]() $X\times \mathbb {P}^m$
is rational for some
$X\times \mathbb {P}^m$
is rational for some
![]() $m\geq 0$
. Hence, a rational variety is stably rational, and a stably rational variety is unirational. The first examples of stably rational nonrational varieties had been given in [Reference Beauville, Colliot-Thélène, Sansuc and Swinnerton-DyerBCTSSD85], where the authors, using Châtelet surfaces, constructed a complex nonrational conic bundle T such that
$m\geq 0$
. Hence, a rational variety is stably rational, and a stably rational variety is unirational. The first examples of stably rational nonrational varieties had been given in [Reference Beauville, Colliot-Thélène, Sansuc and Swinnerton-DyerBCTSSD85], where the authors, using Châtelet surfaces, constructed a complex nonrational conic bundle T such that
![]() $T\times \mathbb {P}^3$
is rational.
$T\times \mathbb {P}^3$
is rational.
In the last decade, important advances on stable rationality have been made, especially for hypersurfaces in projective spaces [Reference VoisinVoi15], [Reference Colliot-Thélène and PirutkaCTP16], [Reference TotaroTot16], [Reference Hassett, Kresch and TschinkelHKT16], [Reference Ahmadinezhad and OkadaAO18], [Reference SchreiederSch18], [Reference Böhning and Graf von BothmerBvB18], [Reference Hassett, Pirutka and TschinkelHPT18], [Reference SchreiederSch19a], [Reference SchreiederSch19b], [Reference Hassett, Pirutka and TschinkelHPT19]. In [Reference Colliot-Thélène and PirutkaCTP16, Theorem 1.17], J. L. Colliot-Thélène and A. Pirutka proved that a very general smooth complex quartic
![]() $3$
-fold is not stably rational. In [Reference SchreiederSch19b, Corollary 1.4], S. Schreieder gave the first examples of unirational nonstably rational smooth hypersurfaces. A. Auel, C. Böhning and A. Pirutka proved that a very general divisor of bidegree
$3$
-fold is not stably rational. In [Reference SchreiederSch19b, Corollary 1.4], S. Schreieder gave the first examples of unirational nonstably rational smooth hypersurfaces. A. Auel, C. Böhning and A. Pirutka proved that a very general divisor of bidegree
![]() $(3,2)$
in
$(3,2)$
in
![]() $\mathbb {P}^3\times \mathbb {P}^2$
, over the complex numbers, is not stably rational. By Theorem 4.7, we get that such a very general divisor is unirational but not stably rational.
$\mathbb {P}^3\times \mathbb {P}^2$
, over the complex numbers, is not stably rational. By Theorem 4.7, we get that such a very general divisor is unirational but not stably rational.
Furthermore, thanks to our unirationality results for divisors of bidegree
![]() $(3,2)$
we get new results on the unirationality of quintic hypersurfaces over
$(3,2)$
we get new results on the unirationality of quintic hypersurfaces over
![]() $C_r$
fields and number fields. The literature on the unirationality of quintics is much less rich than that on quartics. A general quintic hypersurface
$C_r$
fields and number fields. The literature on the unirationality of quintics is much less rich than that on quartics. A general quintic hypersurface
![]() $X_5\subset \mathbb {P}^{n+1}$
, over an algebraically closed field, is unirational if
$X_5\subset \mathbb {P}^{n+1}$
, over an algebraically closed field, is unirational if
![]() $n\geq 17$
[Reference MorinMor38]. Furthermore, a quintic
$n\geq 17$
[Reference MorinMor38]. Furthermore, a quintic
![]() $X_5\subset \mathbb {P}^{n+1}$
containing a
$X_5\subset \mathbb {P}^{n+1}$
containing a
![]() $3$
-plane and otherwise general is unirational if
$3$
-plane and otherwise general is unirational if
![]() $n\geq 6$
[Reference Conte, Marchisio and MurreCMM08]. To the best of our knowledge, these are the only results on the unirationality of quintics.
$n\geq 6$
[Reference Conte, Marchisio and MurreCMM08]. To the best of our knowledge, these are the only results on the unirationality of quintics.
Conventions on the base field, terminology and organization of the paper
All along the paper, the base field k will be of characteristic zero. Let X be a variety over k. When we say that X is rational or unirational, without specifying over which field, we will always mean that X is rational or unirational over k. Similarly, we will say that X has a point or contains a variety with certain properties meaning that X has a k-rational point or contains a variety defined over k with the required properties.
In Section 2, we will introduce the notation, prove some preliminary results about the relation between hypersurfaces in projective spaces and certain divisors in projective bundles and give an immediate generalization of a unirationality criterion due to F. Enriques. In Section 3, we will investigate the unirationality of quartic hypersurfaces and cubic complexes that are complete intersections of a quadric and a cubic. Finally, in Section 4 we will address the unirationality of quintics and divisors in products of projective spaces.
2 Hypersurfaces and divisors in projective bundles
Let
![]() $a_0,\dots ,a_{h+1} \in \mathbb {Z}_{\geq 0}$
be nonnegative integers, and consider the simplicial toric variety
$a_0,\dots ,a_{h+1} \in \mathbb {Z}_{\geq 0}$
be nonnegative integers, and consider the simplicial toric variety
![]() $\mathcal {T}_{a_0,\dots ,a_{h+1}}$
with Cox ring
$\mathcal {T}_{a_0,\dots ,a_{h+1}}$
with Cox ring
![]() $\mathbb {Z}^2$
-grading given, with respect to a fixed basis
$\mathbb {Z}^2$
-grading given, with respect to a fixed basis
![]() $(H_1,H_2)$
of
$(H_1,H_2)$
of
![]() $\operatorname {\mathrm {Pic}}(\mathcal {T}_{a_0,\dots ,a_{h+1}})$
, by the following matrix
$\operatorname {\mathrm {Pic}}(\mathcal {T}_{a_0,\dots ,a_{h+1}})$
, by the following matrix
 $$ \begin{align*}\left(\begin{array}{cccccc} x_0 & \dots & x_{n-h} & y_0 & \dots & y_{h+1}\\ \hline 1 & \dots & 1 & -a_0 & \dots & -a_{h+1}\\ 0 & \dots & 0 & 1 & \dots & 1 \end{array}\right) \end{align*} $$
$$ \begin{align*}\left(\begin{array}{cccccc} x_0 & \dots & x_{n-h} & y_0 & \dots & y_{h+1}\\ \hline 1 & \dots & 1 & -a_0 & \dots & -a_{h+1}\\ 0 & \dots & 0 & 1 & \dots & 1 \end{array}\right) \end{align*} $$
and irrelevant ideal
![]() $(x_0,\dots ,x_{n-h})\cap (y_0,\dots ,y_{h+1})$
. Then
$(x_0,\dots ,x_{n-h})\cap (y_0,\dots ,y_{h+1})$
. Then
with
![]() $\mathcal {E}_{a_0,\dots ,a_{h+1}}\cong \mathcal {O}_{\mathbb {P}^{n-h}}(a_0)\oplus \dots \oplus \mathcal {O}_{\mathbb {P}^{n-h}}(a_{h+1})$
. The secondary fan of
$\mathcal {E}_{a_0,\dots ,a_{h+1}}\cong \mathcal {O}_{\mathbb {P}^{n-h}}(a_0)\oplus \dots \oplus \mathcal {O}_{\mathbb {P}^{n-h}}(a_{h+1})$
. The secondary fan of
![]() $\mathcal {T}_{a_0,\dots ,a_{h+1}}$
is as follows
$\mathcal {T}_{a_0,\dots ,a_{h+1}}$
is as follows

where
![]() $H_1 = (1,0)$
corresponds to the sections
$H_1 = (1,0)$
corresponds to the sections
![]() $x_0,\dots ,x_{n-h}$
,
$x_0,\dots ,x_{n-h}$
,
![]() $H_2 = (0,1)$
, and
$H_2 = (0,1)$
, and
![]() $v_i = (-a_i,1)$
corresponds to the section
$v_i = (-a_i,1)$
corresponds to the section
![]() $y_i$
for
$y_i$
for
![]() $i = 0,\dots ,h+1$
.
$i = 0,\dots ,h+1$
.
Definition 2.1. A divisor
![]() $D\subset \mathcal {T}_{a_0,\dots ,a_{h+1}}$
of multidegree
$D\subset \mathcal {T}_{a_0,\dots ,a_{h+1}}$
of multidegree
![]() $(\delta _{d,0,\dots ,0},\dots ,\delta _{0,\dots ,0,d}; d)$
is a hypersurface given by an equation of the following form
$(\delta _{d,0,\dots ,0},\dots ,\delta _{0,\dots ,0,d}; d)$
is a hypersurface given by an equation of the following form
 $$ \begin{align} D := \left\lbrace\sum_{0\leq i_0\leq \dots \leq i_{h+1}\: |\: i_0+ \dots + i_{h+1}=d}\sigma_{i_0,\dots,i_{h+1}}(x_0,\dots,x_{n-h})y_0^{i_0}\dots y_{h+1}^{i_{h+1}} = 0\right\rbrace\subset \mathcal{T}_{a_0,\dots,a_{h+1}}, \end{align} $$
$$ \begin{align} D := \left\lbrace\sum_{0\leq i_0\leq \dots \leq i_{h+1}\: |\: i_0+ \dots + i_{h+1}=d}\sigma_{i_0,\dots,i_{h+1}}(x_0,\dots,x_{n-h})y_0^{i_0}\dots y_{h+1}^{i_{h+1}} = 0\right\rbrace\subset \mathcal{T}_{a_0,\dots,a_{h+1}}, \end{align} $$
where
![]() $\sigma _{i_0,\dots ,i_{h+1}}\in k[x_0,\dots ,x_{n-h}]_{\delta _{i_0,\dots ,i_{h+1}}}$
and
$\sigma _{i_0,\dots ,i_{h+1}}\in k[x_0,\dots ,x_{n-h}]_{\delta _{i_0,\dots ,i_{h+1}}}$
and
Without loss of generality, we may assume that
![]() $a_0\geq a_1\geq \dots \geq a_{h+1}$
so that (2.3) yields
$a_0\geq a_1\geq \dots \geq a_{h+1}$
so that (2.3) yields
![]() $\delta _{d,0,\dots ,0} \geq \delta _{0,d,0,\dots ,0}\geq \dots \geq \delta _{0,\dots ,0,d}$
.
$\delta _{d,0,\dots ,0} \geq \delta _{0,d,0,\dots ,0}\geq \dots \geq \delta _{0,\dots ,0,d}$
.
Lemma 2.4. Let
![]() $X_d\subset \mathbb {P}^{n+1}$
be a hypersurface of degree d having multiplicity m along an h-plane
$X_d\subset \mathbb {P}^{n+1}$
be a hypersurface of degree d having multiplicity m along an h-plane
![]() $\Lambda $
, and
$\Lambda $
, and
![]() $\widetilde {X}_d$
the blowup of
$\widetilde {X}_d$
the blowup of
![]() $X_d$
along
$X_d$
along
![]() $\Lambda $
with exceptional divisor
$\Lambda $
with exceptional divisor
![]() $\widetilde {E}\subset \widetilde {X}_d$
. Then
$\widetilde {E}\subset \widetilde {X}_d$
. Then
![]() $\widetilde {X}_d$
is isomorphic to a divisor of multidegree
$\widetilde {X}_d$
is isomorphic to a divisor of multidegree
in
![]() $\mathcal {T}_{1,0,\dots ,0}$
, where
$\mathcal {T}_{1,0,\dots ,0}$
, where
![]() $d-j$
is repeated
$d-j$
is repeated
![]() $\binom {h+j}{j}$
times for
$\binom {h+j}{j}$
times for
![]() $j = 0,\dots ,d-m$
. The exceptional divisor
$j = 0,\dots ,d-m$
. The exceptional divisor
![]() $\widetilde {E}$
is a divisor of bidegree
$\widetilde {E}$
is a divisor of bidegree
![]() $(m,d-m)$
in
$(m,d-m)$
in
![]() $\mathbb {P}^{n-h}\times \mathbb {P}^{h}$
.
$\mathbb {P}^{n-h}\times \mathbb {P}^{h}$
.
Proof. We may assume that
![]() $\Lambda = \{z_0 = \dots = z_{n-h} = 0\}$
and
$\Lambda = \{z_0 = \dots = z_{n-h} = 0\}$
and
 $$ \begin{align*}X_d = \left\lbrace \sum_{m_0+\dots+m_{n-h} = m}z_0^{m_0}\dots z_{n-h}^{m_{n-h}}A_{m_0,\dots,m_{n-h}}(z_0,\dots,z_{n+1}) = 0\right\rbrace\subset\mathbb{P}^{n+1}\end{align*} $$
$$ \begin{align*}X_d = \left\lbrace \sum_{m_0+\dots+m_{n-h} = m}z_0^{m_0}\dots z_{n-h}^{m_{n-h}}A_{m_0,\dots,m_{n-h}}(z_0,\dots,z_{n+1}) = 0\right\rbrace\subset\mathbb{P}^{n+1}\end{align*} $$
with
![]() $A_{m_0,\dots ,m_{n-h}}\in k[z_0,\dots ,z_{n+1}]_{d-m}$
. The blowup of
$A_{m_0,\dots ,m_{n-h}}\in k[z_0,\dots ,z_{n+1}]_{d-m}$
. The blowup of
![]() $\mathbb {P}^{n+1}$
along
$\mathbb {P}^{n+1}$
along
![]() $\Lambda $
is the simplicial toric variety
$\Lambda $
is the simplicial toric variety
![]() $\mathcal {T}$
with Cox ring
$\mathcal {T}$
with Cox ring
![]() $\mathbb {Z}^2$
-grading given, with respect to a fixed basis
$\mathbb {Z}^2$
-grading given, with respect to a fixed basis
![]() $(H_1,H_2)$
of
$(H_1,H_2)$
of
![]() $\operatorname {\mathrm {Pic}}(\mathcal {T})$
, by the following matrix:
$\operatorname {\mathrm {Pic}}(\mathcal {T})$
, by the following matrix:
 $$ \begin{align*}\left(\begin{array}{cccccccc} x_0 & \dots & x_{n-h} & y_0 & y_1 & \dots & y_{h+1}\\ \hline 1 & \dots & 1 & 0 & 1 & \dots & 1\\ -1 & \dots & -1 & 1 & 0 & \dots & 0 \end{array}\right) \end{align*} $$
$$ \begin{align*}\left(\begin{array}{cccccccc} x_0 & \dots & x_{n-h} & y_0 & y_1 & \dots & y_{h+1}\\ \hline 1 & \dots & 1 & 0 & 1 & \dots & 1\\ -1 & \dots & -1 & 1 & 0 & \dots & 0 \end{array}\right) \end{align*} $$
and irrelevant ideal
![]() $(x_0,\dots ,x_{n-h})\cap (y_0,\dots ,y_{h+1})$
. Substituting in the above matrix the first row with the sum of the rows and then swapping the rows an multiplying the top row by
$(x_0,\dots ,x_{n-h})\cap (y_0,\dots ,y_{h+1})$
. Substituting in the above matrix the first row with the sum of the rows and then swapping the rows an multiplying the top row by
![]() $-1$
we get to the following grading matrix
$-1$
we get to the following grading matrix
 $$ \begin{align} \left(\begin{array}{cccccccc} x_0 & \dots & x_{n-h} & y_0 & y_1 & \dots & y_{h+1}\\ \hline 1 & \dots & 1 & -1 & 0 & \dots & 0\\ 0 & \dots & 0 & 1 & 1 & \dots & 1 \end{array}\right) \end{align} $$
$$ \begin{align} \left(\begin{array}{cccccccc} x_0 & \dots & x_{n-h} & y_0 & y_1 & \dots & y_{h+1}\\ \hline 1 & \dots & 1 & -1 & 0 & \dots & 0\\ 0 & \dots & 0 & 1 & 1 & \dots & 1 \end{array}\right) \end{align} $$
and hence
![]() $\mathcal {T} = \mathcal {T}_{1,0,\dots ,0}$
. The blow-down morphism is given by
$\mathcal {T} = \mathcal {T}_{1,0,\dots ,0}$
. The blow-down morphism is given by
and the exceptional divisor is
![]() $E = \{y_0 = 0\}$
. Hence, the strict transform of
$E = \{y_0 = 0\}$
. Hence, the strict transform of
![]() $X_d$
is defined by
$X_d$
is defined by
 $$ \begin{align} \widetilde{X}_d = \left\lbrace \sum_{m_0+\dots+m_{n-h} = m}x_0^{m_0}\dots x_{n-h}^{m_{n-h}}A_{m_0,\dots,m_{n-h}}(x_0y_0,\dots,x_{n-h}y_0,y_1,\dots,y_{h+1}) = 0\right\rbrace\subset\mathcal{T}_{1,0,\dots,0}, \end{align} $$
$$ \begin{align} \widetilde{X}_d = \left\lbrace \sum_{m_0+\dots+m_{n-h} = m}x_0^{m_0}\dots x_{n-h}^{m_{n-h}}A_{m_0,\dots,m_{n-h}}(x_0y_0,\dots,x_{n-h}y_0,y_1,\dots,y_{h+1}) = 0\right\rbrace\subset\mathcal{T}_{1,0,\dots,0}, \end{align} $$
and the claim on the multidegree follows. Note that (2.5) yields that
![]() $E \cong \mathbb {P}^{n-h}_{(x_0,\dots ,x_{n-h})}\times \mathbb {P}^h_{(y_1,\dots ,y_{h+1})}$
and hence
$E \cong \mathbb {P}^{n-h}_{(x_0,\dots ,x_{n-h})}\times \mathbb {P}^h_{(y_1,\dots ,y_{h+1})}$
and hence
![]() $\widetilde {E} = \widetilde {X}_d\cap E \subset \mathbb {P}^{n-h}_{(x_0,\dots ,x_{n-h})}\times \mathbb {P}^h_{(y_1,\dots ,y_{h+1})}$
is a divisor of bidegree
$\widetilde {E} = \widetilde {X}_d\cap E \subset \mathbb {P}^{n-h}_{(x_0,\dots ,x_{n-h})}\times \mathbb {P}^h_{(y_1,\dots ,y_{h+1})}$
is a divisor of bidegree
![]() $(m,d-m)$
.
$(m,d-m)$
.
The following is a straightforward generalization of a unirationality criterion for conic bundles due to F. Enriques [Reference Iskovskikh and ProkhorovIP99, Proposition 10.1.1].
Proposition 2.7. Let
![]() $f:X\rightarrow Y$
be a fibration over a unirational variety Y with X an irreducible variety. Assume that there exists a unirational subvariety
$f:X\rightarrow Y$
be a fibration over a unirational variety Y with X an irreducible variety. Assume that there exists a unirational subvariety
![]() $Z\subset X$
such that
$Z\subset X$
such that
![]() $f_{|Z}:Z\rightarrow Y$
is dominant, consider the fiber product
$f_{|Z}:Z\rightarrow Y$
is dominant, consider the fiber product

and denote by
![]() $X_{Z,\eta }$
the generic fiber of
$X_{Z,\eta }$
the generic fiber of
![]() $\widetilde {f}:X_Z\rightarrow Z$
. Assume that
$\widetilde {f}:X_Z\rightarrow Z$
. Assume that
![]() $X_{Z,\eta }$
is integral. Finally, assume that
$X_{Z,\eta }$
is integral. Finally, assume that
![]() $X_{Z,\eta }$
is unirational over
$X_{Z,\eta }$
is unirational over
![]() $k(Z)$
if and only if it has a
$k(Z)$
if and only if it has a
![]() $k(Z)$
-rational point. Then X is unirational.
$k(Z)$
-rational point. Then X is unirational.
Proof. Since
![]() $X_{Z,\eta }$
is integral after replacing Z by an open subset, we may assume that
$X_{Z,\eta }$
is integral after replacing Z by an open subset, we may assume that
![]() $X_Z$
is irreducible.
$X_Z$
is irreducible.
Now, note that the dominant morphism
![]() $f_{|Z}:Z\rightarrow Y$
yields a rational section of
$f_{|Z}:Z\rightarrow Y$
yields a rational section of
![]() $\widetilde {f}:X_Z\rightarrow Z$
. So
$\widetilde {f}:X_Z\rightarrow Z$
. So
![]() $X_{Z,\eta }$
has a
$X_{Z,\eta }$
has a
![]() $k(Z)$
-rational point, and hence, it is unirational over
$k(Z)$
-rational point, and hence, it is unirational over
![]() $k(Z)$
. Therefore,
$k(Z)$
. Therefore,
![]() $X_Z$
is unirational, and hence, X is unirational as well.
$X_Z$
is unirational, and hence, X is unirational as well.
We will apply Proposition 2.7 to fibrations in irreducible m-dimensional quadric or cubic hypersurfaces. In these cases,
![]() $X_{Z,\eta }\subset \mathbb {P}^{m+1}_{k(Z)}$
is an irreducible quadric or cubic hypersurface over
$X_{Z,\eta }\subset \mathbb {P}^{m+1}_{k(Z)}$
is an irreducible quadric or cubic hypersurface over
![]() $k(Z)$
. So after replacing Z by an open subset, we may assume that
$k(Z)$
. So after replacing Z by an open subset, we may assume that
![]() $X_Z$
is irreducible.
$X_Z$
is irreducible.
Remark 2.8. A quadric hypersurface over a field k with a smooth point is rational. Furthermore, by [Reference KollárKol02, Theorem 1.2] a cubic hypersurface of dimension at least two with a point and which is not a cone is unirational.
Definition 2.9. Fix a real number
![]() $r\in \mathbb {R}_{\geq 0}$
. A field k is
$r\in \mathbb {R}_{\geq 0}$
. A field k is
![]() $C_r$
if and only if every homogeneous polynomial
$C_r$
if and only if every homogeneous polynomial
![]() $f\in k[x_0,\dots ,n_n]_d$
of degree
$f\in k[x_0,\dots ,n_n]_d$
of degree
![]() $d> 0$
in
$d> 0$
in
![]() $n+1$
variables with
$n+1$
variables with
![]() $n+1> d^r$
has a nontrivial zero in
$n+1> d^r$
has a nontrivial zero in
![]() $k^{n+1}$
.
$k^{n+1}$
.
Remark 2.10. (Lang’s theorem) If k is a
![]() $C_r$
field,
$C_r$
field,
![]() $f_1,\dots , f_s\in k[x_0,\dots ,n_n]_d$
are homogeneous polynomials of the same degree and
$f_1,\dots , f_s\in k[x_0,\dots ,n_n]_d$
are homogeneous polynomials of the same degree and
![]() $n+1> sd^r$
, then
$n+1> sd^r$
, then
![]() $f_1,\dots ,f_s$
have a nontrivial common zero in
$f_1,\dots ,f_s$
have a nontrivial common zero in
![]() $k^{n+1}$
[Reference PoonenPoo17, Proposition 1.2.6]. Furthermore, if k is
$k^{n+1}$
[Reference PoonenPoo17, Proposition 1.2.6]. Furthermore, if k is
![]() $C_r$
, then
$C_r$
, then
![]() $k(t)$
is
$k(t)$
is
![]() $C_{r+1}$
[Reference PoonenPoo17, Theorem 1.2.7].
$C_{r+1}$
[Reference PoonenPoo17, Theorem 1.2.7].
In the last section, we will need the following.
Proposition 2.11. Let
![]() $D\subset \mathcal {T}_{a_0,\dots ,a_{h+1}}\rightarrow \mathbb {P}^{n-h}$
be a divisor of multidegree
$D\subset \mathcal {T}_{a_0,\dots ,a_{h+1}}\rightarrow \mathbb {P}^{n-h}$
be a divisor of multidegree
![]() $(\delta _{2,0,\dots ,0},\dots ,\delta _{0,\dots ,0,2},2)$
. Then D is birational to a hypersurface
$(\delta _{2,0,\dots ,0},\dots ,\delta _{0,\dots ,0,2},2)$
. Then D is birational to a hypersurface
![]() $X_{\delta _{2,0,\dots ,0}+2}^n\subset \mathbb {P}^{n+1}$
of degree
$X_{\delta _{2,0,\dots ,0}+2}^n\subset \mathbb {P}^{n+1}$
of degree
![]() $\delta _{2,0,\dots ,0}+2$
having multiplicity
$\delta _{2,0,\dots ,0}+2$
having multiplicity
![]() $\delta _{2,0,\dots ,0}$
along an h-plane
$\delta _{2,0,\dots ,0}$
along an h-plane
![]() $\Lambda $
and multiplicity two along an
$\Lambda $
and multiplicity two along an
![]() $(n-h-1)$
-plane
$(n-h-1)$
-plane
![]() $\Lambda '$
such that
$\Lambda '$
such that
![]() $\Lambda \cap \Lambda ' = \emptyset $
.
$\Lambda \cap \Lambda ' = \emptyset $
.
Proof. Write
![]() $D\subset \mathcal {T}_{a_0,\dots ,a_{h+1}}$
as in (2.2) and dehomogenize with respect to
$D\subset \mathcal {T}_{a_0,\dots ,a_{h+1}}$
as in (2.2) and dehomogenize with respect to
![]() $x_{n-h}$
and
$x_{n-h}$
and
![]() $y_{h+1}$
to get an affine hypersurface
$y_{h+1}$
to get an affine hypersurface
Now, we introduce a new variable that we will keep denoting by
![]() $x_{n-h}$
and homogenize f in order to get a polynomial
$x_{n-h}$
and homogenize f in order to get a polynomial
![]() $\overline {f}(x_0,\dots ,x_{n-h-1},y_0,\dots ,y_h,x_{n-h})$
which is homogeneous of degree
$\overline {f}(x_0,\dots ,x_{n-h-1},y_0,\dots ,y_h,x_{n-h})$
which is homogeneous of degree
![]() $\delta _{2,0,\dots ,0}+2$
. Note that
$\delta _{2,0,\dots ,0}+2$
. Note that
![]() $\overline {f}$
has the following form
$\overline {f}$
has the following form
 $$ \begin{align} \overline{f} = \sum_{i_0+\dots +i_{n-h} = \delta_{2,0,\dots,0}}x_0^{i_0}\dots x_{n-h}^{i_{n-h}}A_{i_0,\dots,i_{n-h}}(y_0,\dots,y_h,x_{n-h}) \end{align} $$
$$ \begin{align} \overline{f} = \sum_{i_0+\dots +i_{n-h} = \delta_{2,0,\dots,0}}x_0^{i_0}\dots x_{n-h}^{i_{n-h}}A_{i_0,\dots,i_{n-h}}(y_0,\dots,y_h,x_{n-h}) \end{align} $$
with
![]() $A_{i_0,\dots ,i_{n-h}}\in k[y_0,\dots ,y_h,x_{n-h}]_2$
for all
$A_{i_0,\dots ,i_{n-h}}\in k[y_0,\dots ,y_h,x_{n-h}]_2$
for all
![]() $0\leq i_0\leq \dots \leq i_{n-h}\leq \delta _{2,0,\dots ,0}$
. The hypersurface
$0\leq i_0\leq \dots \leq i_{n-h}\leq \delta _{2,0,\dots ,0}$
. The hypersurface
is birational to X, and hence, it is birational to D as well. To conclude, set
and note that (2.12) yields
![]() $\operatorname {\mathrm {mult}}_{\Lambda }X_{\delta _{2,0,\dots ,0}+2}^n = \delta _{2,0,\dots ,0}$
and
$\operatorname {\mathrm {mult}}_{\Lambda }X_{\delta _{2,0,\dots ,0}+2}^n = \delta _{2,0,\dots ,0}$
and
![]() $\operatorname {\mathrm {mult}}_{\Lambda '}X_{\delta _{2,0,\dots ,0}+2}^n = 2$
.
$\operatorname {\mathrm {mult}}_{\Lambda '}X_{\delta _{2,0,\dots ,0}+2}^n = 2$
.
3 Cubic complexes and Quartics
In this section, we investigate the unirationality of quartic hypersurfaces containing linear subspaces and quadrics, and of complete intersections of quadric and cubic hypersurfaces. The following is an immediate consequence of [Reference Conte, Marchisio and MurreCMM07, Theorem 2.1].
Lemma 3.1. Let
![]() $Y_{2,3} = Y_2 \cap Y_3\subset \mathbb {P}^{n+2}$
with
$Y_{2,3} = Y_2 \cap Y_3\subset \mathbb {P}^{n+2}$
with
![]() $n\geq 3$
be a smooth complete intersection, of a smooth quadric
$n\geq 3$
be a smooth complete intersection, of a smooth quadric
![]() $Y_2$
and a cubic
$Y_2$
and a cubic
![]() $Y_3$
, defined over a field k with
$Y_3$
, defined over a field k with
![]() $\operatorname {\mathrm {char}}(k)\neq 2,3$
. If
$\operatorname {\mathrm {char}}(k)\neq 2,3$
. If
![]() $Y_{2}$
contains a
$Y_{2}$
contains a
![]() $2$
-plane
$2$
-plane
![]() $\Pi $
, then
$\Pi $
, then
![]() $Y_{2,3}$
is unirational.
$Y_{2,3}$
is unirational.
Proof. For
![]() $n = 3$
, the statement has been proven in [Reference Conte, Marchisio and MurreCMM07, Theorem 2.1]. Now, consider the incidence varieties
$n = 3$
, the statement has been proven in [Reference Conte, Marchisio and MurreCMM07, Theorem 2.1]. Now, consider the incidence varieties
 $$ \begin{align*}\begin{array}{ll} W_2 & = \{(y,H) \: | \: y\in H\cap Y_{2}\}\subset Y_{2}\times \mathbb{G}(n-4,n-1); \\ W_3 & = \{(y,H) \: | \: y\in H\cap Y_{3}\}\subset Y_{3}\times \mathbb{G}(n-4,n-1); \\ W_{2,3} & = \{(y,H) \: | \: y\in H\cap Y_{2,3}\} = W_2\cap W_3\subset Y_{2,3}\times \mathbb{G}(n-4,n-1), \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ll} W_2 & = \{(y,H) \: | \: y\in H\cap Y_{2}\}\subset Y_{2}\times \mathbb{G}(n-4,n-1); \\ W_3 & = \{(y,H) \: | \: y\in H\cap Y_{3}\}\subset Y_{3}\times \mathbb{G}(n-4,n-1); \\ W_{2,3} & = \{(y,H) \: | \: y\in H\cap Y_{2,3}\} = W_2\cap W_3\subset Y_{2,3}\times \mathbb{G}(n-4,n-1), \end{array} \end{align*} $$
where
![]() $\mathbb {G}(n-4,n-1)$
is the Grassmannian of
$\mathbb {G}(n-4,n-1)$
is the Grassmannian of
![]() $5$
-planes in
$5$
-planes in
![]() $\mathbb {P}^{n+2}$
containing
$\mathbb {P}^{n+2}$
containing
![]() $\Pi $
. Let
$\Pi $
. Let
![]() $W_{2,\eta }, W_{3,\eta }, W_{2,3,\eta }$
be the generic fibers of the second projection onto
$W_{2,\eta }, W_{3,\eta }, W_{2,3,\eta }$
be the generic fibers of the second projection onto
![]() $\mathbb {G}(n-4,n-1)$
from
$\mathbb {G}(n-4,n-1)$
from
![]() $W_2,W_3,W_{2,3}$
, respectively.
$W_2,W_3,W_{2,3}$
, respectively.
The
![]() $2$
-plane
$2$
-plane
![]() $\Pi \subset Y_{2}$
yields a
$\Pi \subset Y_{2}$
yields a
![]() $2$
-plane
$2$
-plane
![]() $\Pi '\subset W_{2,\eta }$
defined over
$\Pi '\subset W_{2,\eta }$
defined over
![]() $k(t_1,\dots ,t_{3(n-3)})$
, and since
$k(t_1,\dots ,t_{3(n-3)})$
, and since
![]() $Y_2$
is smooth, we have that
$Y_2$
is smooth, we have that
![]() $W_{2,\eta }$
is smooth.
$W_{2,\eta }$
is smooth.
Hence,
![]() $W_{2,3,\eta }\subset \mathbb {P}^5_{k(t_1,\dots ,t_{3(n-3)})}$
is a smooth complete intersection over
$W_{2,3,\eta }\subset \mathbb {P}^5_{k(t_1,\dots ,t_{3(n-3)})}$
is a smooth complete intersection over
![]() $k(t_1,\dots ,t_{3(n-3)})$
of a quadric and a cubic satisfying the hypotheses of [Reference Conte, Marchisio and MurreCMM07, Theorem 2.1], and so
$k(t_1,\dots ,t_{3(n-3)})$
of a quadric and a cubic satisfying the hypotheses of [Reference Conte, Marchisio and MurreCMM07, Theorem 2.1], and so
![]() $W_{2,3,\eta }$
is unirational over the function field
$W_{2,3,\eta }$
is unirational over the function field
![]() $k(t_1,\dots ,t_{3(n-3)})$
. As in the proof of Proposition 2.7, after replacing
$k(t_1,\dots ,t_{3(n-3)})$
. As in the proof of Proposition 2.7, after replacing
![]() $\mathbb {G}(n-4,n-1)$
by an open subset we may assume that
$\mathbb {G}(n-4,n-1)$
by an open subset we may assume that
![]() $W_{2,3}$
is irreducible.
$W_{2,3}$
is irreducible.
Therefore,
![]() $W_{2,3}$
is unirational over the base field k, and to conclude it is enough to observe that the first projection
$W_{2,3}$
is unirational over the base field k, and to conclude it is enough to observe that the first projection
![]() $W_{2,3}\rightarrow Y_{2,3}$
is dominant.
$W_{2,3}\rightarrow Y_{2,3}$
is dominant.
Lemma 3.2. Let
![]() $Q_0\subset \mathbb {P}^{n+1}$
be a smooth
$Q_0\subset \mathbb {P}^{n+1}$
be a smooth
![]() $(n-1)$
-dimensional quadric and
$(n-1)$
-dimensional quadric and
![]() $X_d\subset \mathbb {P}^{n+1}$
an irreducible hypersurface of degree d containing
$X_d\subset \mathbb {P}^{n+1}$
an irreducible hypersurface of degree d containing
![]() $Q_0$
with multiplicity one and otherwise general. Then there exists a complete intersection
$Q_0$
with multiplicity one and otherwise general. Then there exists a complete intersection
of a quadric
![]() $Y_2$
and a hypersurface
$Y_2$
and a hypersurface
![]() $Y_{d-1}$
of degree
$Y_{d-1}$
of degree
![]() $d-1$
such that:
$d-1$
such that:
-
(i)
 $Y_{2,d-1}$
has a point
$Y_{2,d-1}$
has a point
 $v\in Y_{2,d-1}$
of multiplicity
$v\in Y_{2,d-1}$
of multiplicity
 $d-2$
, and
$d-2$
, and -
(ii) the linear projection from v yields a birational map
 .
.
Furthermore,
![]() $Y_2$
is smooth and
$Y_2$
is smooth and
![]() $\operatorname {\mathrm {mult}}_{v}Y_{d-1} = d-2$
.
$\operatorname {\mathrm {mult}}_{v}Y_{d-1} = d-2$
.
Proof. We may write
![]() $Q_0 = \{z_1 = Q = 0\}$
with
$Q_0 = \{z_1 = Q = 0\}$
with
![]() $Q\in k[z_0,\dots ,z_{n+1}]_2$
. Then
$Q\in k[z_0,\dots ,z_{n+1}]_2$
. Then
![]() $X_d$
is of the form
$X_d$
is of the form
with
![]() $A\in k[z_0,\dots ,z_{n+1}]_{d-1}$
and
$A\in k[z_0,\dots ,z_{n+1}]_{d-1}$
and
![]() $B\in k[z_0,\dots ,z_{n+1}]_{d-2}$
. Consider the quadric
$B\in k[z_0,\dots ,z_{n+1}]_{d-2}$
. Consider the quadric
![]() $Y_2 = \{z_1u-Q = 0\}$
with
$Y_2 = \{z_1u-Q = 0\}$
with
![]() $z_0,\dots ,z_{n+1},u$
homogeneous coordinates on
$z_0,\dots ,z_{n+1},u$
homogeneous coordinates on
![]() $\mathbb {P}^{n+2}$
. Since
$\mathbb {P}^{n+2}$
. Since
![]() $Q_0$
is smooth, we may assume that
$Q_0$
is smooth, we may assume that
![]() $Q = z_0^2+\dots + z_{n+1}^2$
. Hence,
$Q = z_0^2+\dots + z_{n+1}^2$
. Hence,
![]() $Y_2$
is a smooth as well.
$Y_2$
is a smooth as well.
Denote by
![]() $CX_d$
,
$CX_d$
,
![]() $CQ_0$
the cones, respectively, over
$CQ_0$
the cones, respectively, over
![]() $X_d$
and
$X_d$
and
![]() $Q_0$
with vertex
$Q_0$
with vertex
![]() $v = [0:\dots :0:1]$
. Then
$v = [0:\dots :0:1]$
. Then
![]() $CQ_0\subset Y_2$
and
$CQ_0\subset Y_2$
and
Set
![]() $Y_{d-1} = \{A+uB = 0\}$
and
$Y_{d-1} = \{A+uB = 0\}$
and
![]() $Y_{2,d-1} = \{z_1u-Q = A+uB = 0\}$
. Note that the tangent space of
$Y_{2,d-1} = \{z_1u-Q = A+uB = 0\}$
. Note that the tangent space of
![]() $Y_2$
at v is the hyperplane
$Y_2$
at v is the hyperplane
![]() $\{z_1 = 0\}$
, the tangent cone of
$\{z_1 = 0\}$
, the tangent cone of
![]() $Y_{d-1}$
at v is given by
$Y_{d-1}$
at v is given by
![]() $\{B = 0\}$
and the tangent cone of
$\{B = 0\}$
and the tangent cone of
![]() $Y_{2,d-1}$
at v is cut out by
$Y_{2,d-1}$
at v is cut out by
![]() $\{z_1 = B = 0\}$
. Hence,
$\{z_1 = B = 0\}$
. Hence,
Therefore, if
![]() $p\in Y_{2,d-1}$
is a general point the line
$p\in Y_{2,d-1}$
is a general point the line
![]() $\left \langle v,p\right \rangle $
intersects
$\left \langle v,p\right \rangle $
intersects
![]() $Y_{2,d-1}$
just in v with multiplicity
$Y_{2,d-1}$
just in v with multiplicity
![]() $d-2$
and in p with multiplicity one. So the projection
$d-2$
and in p with multiplicity one. So the projection
![]() is birational onto
is birational onto
![]() $\overline {\pi _{v}(Y_{2,d-1})}$
which must then be a hypersurface of degree
$\overline {\pi _{v}(Y_{2,d-1})}$
which must then be a hypersurface of degree
![]() $2(d-1)-(d-2) = d$
. To conclude, it is enough to note that since
$2(d-1)-(d-2) = d$
. To conclude, it is enough to note that since
![]() $Y_{2,d-1}$
is not a cone of vertex v and
$Y_{2,d-1}$
is not a cone of vertex v and
![]() $Y_{2,d-1}\subset CX_d$
we have
$Y_{2,d-1}\subset CX_d$
we have
![]() $\overline {\pi _{v}(Y_{2,d-1})} = X_d$
.
$\overline {\pi _{v}(Y_{2,d-1})} = X_d$
.
Lemma 3.3. Consider the complete intersection
where
![]() $Y_2 = \{z_1u-A_1 = 0\}\subset \mathbb {P}^{n+2}_{(z_0,\dots ,z_{n-1},u)}$
and
$Y_2 = \{z_1u-A_1 = 0\}\subset \mathbb {P}^{n+2}_{(z_0,\dots ,z_{n-1},u)}$
and
with
![]() $A_i$
general homogeneous polynomial of degree two. Assume that the
$A_i$
general homogeneous polynomial of degree two. Assume that the
![]() $(n-2)$
-dimensional quadric
$(n-2)$
-dimensional quadric
![]() $\overline {Q} = \{z_0 = z_1 = A_1 = 0\}$
has a point.
$\overline {Q} = \{z_0 = z_1 = A_1 = 0\}$
has a point.
Then there exists a variety W, with a surjective morphism onto a rational surface S, such that if W is unirational, then there is a dominant rational map
![]() and hence
and hence
![]() $Y_{2,d-1}$
is unirational as well. Furthermore, the general fiber of
$Y_{2,d-1}$
is unirational as well. Furthermore, the general fiber of
![]() $W\rightarrow S$
is a complete intersection of a quadric and a hypersurface of degree
$W\rightarrow S$
is a complete intersection of a quadric and a hypersurface of degree
![]() $d-3$
.
$d-3$
.
Proof. Set
![]() $v = [0:\dots :0:1]$
and
$v = [0:\dots :0:1]$
and
![]() $H = \{z_0 = z_1 = 0\}\subset \mathbb {P}^{n+2}$
. Then
$H = \{z_0 = z_1 = 0\}\subset \mathbb {P}^{n+2}$
. Then
Take a general point
![]() $p\in H$
. The lines through p that intersect
$p\in H$
. The lines through p that intersect
![]() $Y_{d-1}$
at p with multiplicity at least
$Y_{d-1}$
at p with multiplicity at least
![]() $d-2$
are parametrized by a hypersurface
$d-2$
are parametrized by a hypersurface
![]() $W_{d-3}$
cut out in the
$W_{d-3}$
cut out in the
![]() $(n+1)$
-dimensional projective space
$(n+1)$
-dimensional projective space
![]() $\mathbb {P}(T_p\mathbb {P}^{n+2})$
of lines through p by a polynomial in
$\mathbb {P}(T_p\mathbb {P}^{n+2})$
of lines through p by a polynomial in
![]() $k[z_0,z_1]_{d-3}$
.
$k[z_0,z_1]_{d-3}$
.
Now, consider the cone
![]() $C\overline {Q}$
over the
$C\overline {Q}$
over the
![]() $(n-2)$
-dimensional quadric
$(n-2)$
-dimensional quadric
![]() $\overline {Q} = \{z_0 = z_1 = A_1 = 0\}$
, and take a general point
$\overline {Q} = \{z_0 = z_1 = A_1 = 0\}$
, and take a general point
![]() $p \in C\overline {Q}$
. Note that
$p \in C\overline {Q}$
. Note that
![]() $C\overline {Q}\subset Y_2$
. The lines through p that are contained in
$C\overline {Q}\subset Y_2$
. The lines through p that are contained in
![]() $Y_2$
are parametrized by a quadric hypersurface
$Y_2$
are parametrized by a quadric hypersurface
![]() $W_2\subset \mathbb {P}(T_pY_2)$
.
$W_2\subset \mathbb {P}(T_pY_2)$
.
Let
![]() $\mathcal {F} = \mathcal {T}_{Y_2|C\overline {Q}}$
be the restriction of the tangent sheaf of
$\mathcal {F} = \mathcal {T}_{Y_2|C\overline {Q}}$
be the restriction of the tangent sheaf of
![]() $Y_2$
to
$Y_2$
to
![]() $C\overline {Q}$
. Summing up, there is a subvariety
$C\overline {Q}$
. Summing up, there is a subvariety
![]() $W_{2,d-3}\subset \mathbb {P}(\mathcal {F})$
with a surjective morphism
$W_{2,d-3}\subset \mathbb {P}(\mathcal {F})$
with a surjective morphism
![]() $\rho :W_{2,d-3}\rightarrow C\overline {Q}$
whose fiber over a general point of
$\rho :W_{2,d-3}\rightarrow C\overline {Q}$
whose fiber over a general point of
![]() $p\in C\overline {Q}$
is a complete intersection of a quadric and a hypersurface of degree
$p\in C\overline {Q}$
is a complete intersection of a quadric and a hypersurface of degree
![]() $d-3$
in
$d-3$
in
![]() $\mathbb {P}^{n}$
. Hence,
$\mathbb {P}^{n}$
. Hence,
![]() $\dim (W_{2,d-3}) = 2n-3$
.
$\dim (W_{2,d-3}) = 2n-3$
.
By hypothesis,
![]() $\overline {Q}$
has a point. Let
$\overline {Q}$
has a point. Let
![]() $\overline {C}$
be a conic in
$\overline {C}$
be a conic in
![]() $\overline {Q}$
through this point and S the cone over
$\overline {Q}$
through this point and S the cone over
![]() $\overline {C}$
with vertex v. Then
$\overline {C}$
with vertex v. Then
![]() $S\subset C\overline {Q}$
is a rational surface. Set
$S\subset C\overline {Q}$
is a rational surface. Set
![]() $W = \rho ^{-1}(S)$
and
$W = \rho ^{-1}(S)$
and
![]() $W_s = \rho ^{-1}(s)$
for
$W_s = \rho ^{-1}(s)$
for
![]() $s\in S$
. A general point
$s\in S$
. A general point
![]() $w\in W$
represents a pair
$w\in W$
represents a pair
![]() $(s,l_s)$
, where
$(s,l_s)$
, where
![]() $s\in S$
and
$s\in S$
and
![]() $l_s$
is a line through s which is contained in
$l_s$
is a line through s which is contained in
![]() $Y_2$
and intersects
$Y_2$
and intersects
![]() $Y_{d-1}$
with multiplicity
$Y_{d-1}$
with multiplicity
![]() $d-2$
at s. Since
$d-2$
at s. Since
![]() $\deg (Y_{d-1}) = d-1$
the line
$\deg (Y_{d-1}) = d-1$
the line
![]() $l_s$
intersects
$l_s$
intersects
![]() $Y_{d-1}$
just at one more point
$Y_{d-1}$
just at one more point
![]() $x_{(s,l_s)}\in Y_2 \cap Y_{d-1} = Y_{2,d-1}$
and we get a rational map
$x_{(s,l_s)}\in Y_2 \cap Y_{d-1} = Y_{2,d-1}$
and we get a rational map
If W is unirational, in order to prove that
![]() $\psi $
is dominant it is enough to prove that the induced map
$\psi $
is dominant it is enough to prove that the induced map
between the algebraic closures is dominant. Take a general point
![]() $p \in \overline {Y}_{2,d-1}$
, and assume that
$p \in \overline {Y}_{2,d-1}$
, and assume that
![]() $x_{(s,l_s)} = p$
. Then
$x_{(s,l_s)} = p$
. Then
![]() $l_s$
lies in the tangent space of
$l_s$
lies in the tangent space of
![]() $Y_2$
at p which is given by
$Y_2$
at p which is given by
![]() $\{L = 0\}$
. Such tangent space intersects
$\{L = 0\}$
. Such tangent space intersects
![]() $\overline {S}$
in a conic, and further intersecting with
$\overline {S}$
in a conic, and further intersecting with
![]() $W_{d-3}$
we see that there are finitely may points
$W_{d-3}$
we see that there are finitely may points
![]() $s\in \overline {S}$
such that
$s\in \overline {S}$
such that
![]() $x_{(s,l_s)} = p$
for some
$x_{(s,l_s)} = p$
for some
![]() $l_s\in W_s$
. Furthermore, if
$l_s\in W_s$
. Furthermore, if
![]() $x_{(s,l_s)} = x_{(s,l_s')}$
, then
$x_{(s,l_s)} = x_{(s,l_s')}$
, then
![]() $l_s = l_s'$
. Hence,
$l_s = l_s'$
. Hence,
![]() $\overline {\psi }$
is generically finite and since
$\overline {\psi }$
is generically finite and since
![]() $\dim (W) = \dim (Y_{2,d-1})$
we conclude that
$\dim (W) = \dim (Y_{2,d-1})$
we conclude that
![]() $\overline {\psi }$
is dominant.
$\overline {\psi }$
is dominant.
Proposition 3.4. Let
![]() $X_d\subset \mathbb {P}^{n+1}$
be a hypersurface of degree d having multiplicity
$X_d\subset \mathbb {P}^{n+1}$
be a hypersurface of degree d having multiplicity
![]() $d-2$
along an
$d-2$
along an
![]() $(n-1)$
-plane
$(n-1)$
-plane
![]() $\Lambda \subset \mathbb {P}^{n+1}$
. Assume that there is a quadric
$\Lambda \subset \mathbb {P}^{n+1}$
. Assume that there is a quadric
![]() $Q_p$
in the quadric fibration induced by the projection from
$Q_p$
in the quadric fibration induced by the projection from
![]() $\Lambda $
such that the quadric
$\Lambda $
such that the quadric
![]() $Q_p\cap \Lambda $
is smooth and has a point and that
$Q_p\cap \Lambda $
is smooth and has a point and that
![]() $X_d$
is otherwise general.
$X_d$
is otherwise general.
Then there exist a rational surface S and a variety W with a morphism onto S such that if W is unirational, then there is a dominant rational map
![]() and hence
and hence
![]() $X_d$
is unirational as well.
$X_d$
is unirational as well.
Proof. We may write
![]() $\Lambda = \{z_0 = z_1 = 0\}$
and
$\Lambda = \{z_0 = z_1 = 0\}$
and
with
![]() $A_i \in k[z_0,\dots ,z_{n+1}]_2$
. Note that
$A_i \in k[z_0,\dots ,z_{n+1}]_2$
. Note that
![]() $X_d$
contains the smooth
$X_d$
contains the smooth
![]() $(n-1)$
-dimensional quadric
$(n-1)$
-dimensional quadric
![]() $Q_p = \{z_1 = A_1 = 0\}$
. Hence, by Lemma 3.2 there is an irreducible complete intersection
$Q_p = \{z_1 = A_1 = 0\}$
. Hence, by Lemma 3.2 there is an irreducible complete intersection
![]() $Y_{2,d-1}\subset \mathbb {P}^{n+2}$
which is birational to
$Y_{2,d-1}\subset \mathbb {P}^{n+2}$
which is birational to
![]() $X_d$
.
$X_d$
.
Consider the quadric
![]() $Y_2 = \{z_1u-A_1 = 0\}\subset \mathbb {P}^{n+2}$
with homogeneous coordinates
$Y_2 = \{z_1u-A_1 = 0\}\subset \mathbb {P}^{n+2}$
with homogeneous coordinates
![]() $z_0,\dots ,z_{n+1},u$
, and let
$z_0,\dots ,z_{n+1},u$
, and let
![]() $CX_d$
be the cone over
$CX_d$
be the cone over
![]() $X_d$
as in the proof of Lemma 3.2. The intersection
$X_d$
as in the proof of Lemma 3.2. The intersection
![]() $Y_2\cap CX_d$
has two components: the cone
$Y_2\cap CX_d$
has two components: the cone
![]() $CQ_p$
over
$CQ_p$
over
![]() $Q_p$
and the degree
$Q_p$
and the degree
![]() $d-1$
hypersurface
$d-1$
hypersurface
Let
![]() $W\rightarrow S$
be the fibration constructed in Lemma 3.3 starting from the complete intersection
$W\rightarrow S$
be the fibration constructed in Lemma 3.3 starting from the complete intersection
![]() $Y_{2,d-1} = Y_2\cap Y_{d-1}$
. If W is unirational, Lemma 3.3 yields a dominant rational map
$Y_{2,d-1} = Y_2\cap Y_{d-1}$
. If W is unirational, Lemma 3.3 yields a dominant rational map
. Finally, let
be the dominant rational map in Lemma 3.2. By considering the composition

we get a dominant rational map
, and hence
![]() $X_d$
is unirational.
$X_d$
is unirational.
Proposition 3.5. Let
![]() $Y_{2,3} = Y_2\cap Y_3\subset \mathbb {P}^{n+2}$
be a complete intersection of a quadric and a cubic of the following form
$Y_{2,3} = Y_2\cap Y_3\subset \mathbb {P}^{n+2}$
be a complete intersection of a quadric and a cubic of the following form
with
![]() $A,B,C\in k[z_0,\dots ,z_{n+1}]_2$
general. If the quadric
$A,B,C\in k[z_0,\dots ,z_{n+1}]_2$
general. If the quadric
![]() $\overline {Q} = \{z_0 = z_1 = A = 0\}$
is smooth and has a point, then
$\overline {Q} = \{z_0 = z_1 = A = 0\}$
is smooth and has a point, then
![]() $Y_{2,3}$
is unirational.
$Y_{2,3}$
is unirational.
Proof. By Lemma 3.3 with
![]() $d = 4$
, there exists a variety W with a morphism onto a rational surface S whose general fiber is a complete intersection of a quadric and a hyperplane. Hence, W has a structure of quadric bundle
$d = 4$
, there exists a variety W with a morphism onto a rational surface S whose general fiber is a complete intersection of a quadric and a hyperplane. Hence, W has a structure of quadric bundle
![]() $W\rightarrow S$
over S with
$W\rightarrow S$
over S with
![]() $(n-2)$
-dimensional quadrics as fibers.
$(n-2)$
-dimensional quadrics as fibers.
By the proof of Lemma 3.3, S is a cone over a conic and it is contained in
![]() $Y_2 = \{uz_1 - A = 0\}$
. In particular, any line in S through its vertex is contained in
$Y_2 = \{uz_1 - A = 0\}$
. In particular, any line in S through its vertex is contained in
![]() $Y_2$
. Moreover, S is contained in the intersection of
$Y_2$
. Moreover, S is contained in the intersection of
![]() $Y_3$
with its tangent cone at v. Hence, the lines in S through its vertex yield a section of the quadric bundle
$Y_3$
with its tangent cone at v. Hence, the lines in S through its vertex yield a section of the quadric bundle
![]() $W\rightarrow S$
and so W is rational. Finally, to conclude it is enough to apply Lemma 3.3.
$W\rightarrow S$
and so W is rational. Finally, to conclude it is enough to apply Lemma 3.3.
Corollary 3.6. Let
![]() $X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface having multiplicity two along an
$X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface having multiplicity two along an
![]() $(n-1)$
-plane
$(n-1)$
-plane
![]() $\Lambda \subset \mathbb {P}^{n+1}$
with
$\Lambda \subset \mathbb {P}^{n+1}$
with
![]() $n\geq 3$
. Assume that there is a quadric
$n\geq 3$
. Assume that there is a quadric
![]() $Q_p$
in the quadric fibration induced by the projection from
$Q_p$
in the quadric fibration induced by the projection from
![]() $\Lambda $
such that the quadric
$\Lambda $
such that the quadric
![]() $Q_{\Lambda } = Q_p\cap \Lambda $
is smooth and has a point and that
$Q_{\Lambda } = Q_p\cap \Lambda $
is smooth and has a point and that
![]() $X_4$
is otherwise general. Then
$X_4$
is otherwise general. Then
![]() $X_4$
is unirational.
$X_4$
is unirational.
Proof. Up to a change of coordinates, we may assume that
![]() $\Lambda = \{z_0 = z_1 = 0\}$
,
$\Lambda = \{z_0 = z_1 = 0\}$
,
![]() $X_4$
is given by
$X_4$
is given by
and
![]() $Q_{\Lambda } = \{z_1 = A = 0\}$
. The intersection
$Q_{\Lambda } = \{z_1 = A = 0\}$
. The intersection
![]() $\{z_1u-A = z_0^2A+z_0z_1B+z_1^2C = 0\}\subset \mathbb {P}^{n+2}_{(z_0,\dots ,z_{n+1},u)}$
has two components:
$\{z_1u-A = z_0^2A+z_0z_1B+z_1^2C = 0\}\subset \mathbb {P}^{n+2}_{(z_0,\dots ,z_{n+1},u)}$
has two components:
![]() $\{z_1 = A = 0\}$
and
$\{z_1 = A = 0\}$
and
By Lemma 3.2 and its proof, there exists a birational map
![]() . To conclude, it is enough to note that
. To conclude, it is enough to note that
![]() $Y_{2,3}$
is a complete intersection of the form covered by Proposition 3.5.
$Y_{2,3}$
is a complete intersection of the form covered by Proposition 3.5.
Corollary 3.7. Let
![]() $X_4\subset \mathbb {P}^{n+1}$
, with
$X_4\subset \mathbb {P}^{n+1}$
, with
![]() $n\geq 5$
, be a quartic hypersurface containing an
$n\geq 5$
, be a quartic hypersurface containing an
![]() $(n-1)$
-dimensional smooth quadric
$(n-1)$
-dimensional smooth quadric
![]() $Q_0$
which contains a
$Q_0$
which contains a
![]() $2$
-plane and otherwise general. Then
$2$
-plane and otherwise general. Then
![]() $X_4$
is unirational.
$X_4$
is unirational.
Proof. By Lemma 3.2,
![]() $X_4$
is birational to a complete intersection
$X_4$
is birational to a complete intersection
![]() $Y_{2,3} = Y_2\cap Y_3$
, where
$Y_{2,3} = Y_2\cap Y_3$
, where
![]() $Y_2$
is a smooth quadric. By the proof of Lemma 3.2, we have that since
$Y_2$
is a smooth quadric. By the proof of Lemma 3.2, we have that since
![]() $Q_0$
contains a
$Q_0$
contains a
![]() $2$
-plane
$2$
-plane
![]() $Y_2$
contains a
$Y_2$
contains a
![]() $2$
-plane as well. Hence,
$2$
-plane as well. Hence,
![]() $Y_2$
is a smooth quadric containing a
$Y_2$
is a smooth quadric containing a
![]() $2$
-plane and we conclude by Lemma 3.1.
$2$
-plane and we conclude by Lemma 3.1.
Corollary 3.8. Let
![]() $X_4\subset \mathbb {P}^{n+1}$
, with
$X_4\subset \mathbb {P}^{n+1}$
, with
![]() $n\geq 2$
, be a quartic hypersurface having multiplicity two along an
$n\geq 2$
, be a quartic hypersurface having multiplicity two along an
![]() $(n-1)$
-dimensional smooth quadric Q, with a point and otherwise general. Then
$(n-1)$
-dimensional smooth quadric Q, with a point and otherwise general. Then
![]() $X_4$
is unirational.
$X_4$
is unirational.
Proof. Slightly modifying the proof of Lemma 3.2, we see that in this case
![]() $X_4$
is birational to a complete intersection
$X_4$
is birational to a complete intersection
![]() $Y_2\cap Y_2'\subset \mathbb {P}^{n+2}$
of two quadrics, and hence, the claim follows from [Reference Colliot-Thélène, Sansuc and Swinnerton-DyerCTSSD87, Proposition 2.3].
$Y_2\cap Y_2'\subset \mathbb {P}^{n+2}$
of two quadrics, and hence, the claim follows from [Reference Colliot-Thélène, Sansuc and Swinnerton-DyerCTSSD87, Proposition 2.3].
In the following, we will investigate the unirationality of quartic hypersurfaces by constructing explicit birational maps to divisors in products of projective spaces. In particular, we will get an improvement of Corollary 3.6 when
![]() $n\geq 4$
.
$n\geq 4$
.
Lemma 3.9. Consider the hypersurface
where
![]() $A_i = A_i^2 + z_0A_i^1+z_0^2A_i^0$
, and
$A_i = A_i^2 + z_0A_i^1+z_0^2A_i^0$
, and
![]() $L,A_i^1\in k[z_1,\dots ,z_{n+1}]_1$
,
$L,A_i^1\in k[z_1,\dots ,z_{n+1}]_1$
,
![]() $Q,A_i^2\in k[z_1,\dots ,z_{n+1}]_2$
,
$Q,A_i^2\in k[z_1,\dots ,z_{n+1}]_2$
,
![]() $A_i^0\in k$
for
$A_i^0\in k$
for
![]() $i = 1,\dots ,d-2$
. Then
$i = 1,\dots ,d-2$
. Then
![]() $X_d$
is birational to the divisor
$X_d$
is birational to the divisor
 $$ \begin{align*}Y_{(d-1,2)} = \left\{\sum_{i=0}^{d-1}x_0^{d-1-i}x_1^iB_i = 0\right\}\subset\mathbb{P}^1_{(x_0,x_1)}\times \mathbb{P}^{n}_{(w_1,\dots, w_{n+1})} \end{align*} $$
$$ \begin{align*}Y_{(d-1,2)} = \left\{\sum_{i=0}^{d-1}x_0^{d-1-i}x_1^iB_i = 0\right\}\subset\mathbb{P}^1_{(x_0,x_1)}\times \mathbb{P}^{n}_{(w_1,\dots, w_{n+1})} \end{align*} $$
of bidegree
![]() $(d-1,2)$
, where
$(d-1,2)$
, where
![]() $B_0 = w_1L+A_1^0w_1^2$
,
$B_0 = w_1L+A_1^0w_1^2$
,
![]() $B_1 = Q+w_1A_1^1+w_1^2A_2^0$
,
$B_1 = Q+w_1A_1^1+w_1^2A_2^0$
,
![]() $B_j = A_{j-1}^2+w_1A_j^1+w_1^2A_{j+1}^0$
for
$B_j = A_{j-1}^2+w_1A_j^1+w_1^2A_{j+1}^0$
for
![]() $j = 2,\dots ,d-3$
,
$j = 2,\dots ,d-3$
,
![]() $B_{d-2} = A_{d-3}^2+w_1A_{d-2}^1$
,
$B_{d-2} = A_{d-3}^2+w_1A_{d-2}^1$
,
![]() $B_{d-1} = A_{d-2}^2$
.
$B_{d-1} = A_{d-2}^2$
.
Proof. Note that
![]() $X_d$
passes through the point
$X_d$
passes through the point
![]() $p = [1:0:\dots :0]$
, and the rational map
$p = [1:0:\dots :0]$
, and the rational map

is birational with birational inverse

where
![]() $L = L(w_1,\dots ,w_{n+1})$
. Note that
$L = L(w_1,\dots ,w_{n+1})$
. Note that
![]() $\varphi ^{-1}$
contracts the divisor
$\varphi ^{-1}$
contracts the divisor
![]() $\{L = 0\}$
to the point p. The strict transform of
$\{L = 0\}$
to the point p. The strict transform of
![]() $X_d$
via
$X_d$
via
![]() $\varphi ^{-1}$
is given by
$\varphi ^{-1}$
is given by
 $$ \begin{align*}\widetilde{X}_d = \{w_0^{d-2}(w_0w_1L+LQ) &+ w_0^{d-3}(w_0^2w_1^2A_1^0 + w_0w_1LA_1^1+L^2A_1^2)+ \dots\\ &+L^{d-3}(w_0^2w_1^2A_{d-2}^0 + w_0w_1LA_{d-2}^1+L^2A_{d-2}^2)=0\}, \end{align*} $$
$$ \begin{align*}\widetilde{X}_d = \{w_0^{d-2}(w_0w_1L+LQ) &+ w_0^{d-3}(w_0^2w_1^2A_1^0 + w_0w_1LA_1^1+L^2A_1^2)+ \dots\\ &+L^{d-3}(w_0^2w_1^2A_{d-2}^0 + w_0w_1LA_{d-2}^1+L^2A_{d-2}^2)=0\}, \end{align*} $$
which we rewrite as
 $$ \begin{align*}\widetilde{X}_d = \{w_0^{d-1}(w_1L+w_1^2A_1^0)& +w_0^{d-2}L(Q+w_1A_1^1+w_1^2A_2^0)+\dots\\ & +w_0L^{d-2}(A_{d-3}^2+w_1A_{d-2}^1) + L^{d-1}A_{d-2}^2 = 0\}. \end{align*} $$
$$ \begin{align*}\widetilde{X}_d = \{w_0^{d-1}(w_1L+w_1^2A_1^0)& +w_0^{d-2}L(Q+w_1A_1^1+w_1^2A_2^0)+\dots\\ & +w_0L^{d-2}(A_{d-3}^2+w_1A_{d-2}^1) + L^{d-1}A_{d-2}^2 = 0\}. \end{align*} $$
Finally, substituting
![]() $w_0 = \frac {x_0}{x_1}L$
we get the equation cutting out the divisor
$w_0 = \frac {x_0}{x_1}L$
we get the equation cutting out the divisor
![]() $Y_{(d-1,2)}\subset \mathbb {P}^1_{(x_0,x_1)}\times \mathbb {P}^{n}_{(w_1:\dots : w_{n+1})}$
in the statement.
$Y_{(d-1,2)}\subset \mathbb {P}^1_{(x_0,x_1)}\times \mathbb {P}^{n}_{(w_1:\dots : w_{n+1})}$
in the statement.
Proposition 3.10. Let
![]() $Y_{(3,2)}$
be a general divisor of the form
$Y_{(3,2)}$
be a general divisor of the form
 $$ \begin{align*}Y_{(3,2)} = \left\{\sum_{i=0}^{3}x_0^{3-i}x_1^iB_i = 0\right\}\subset\mathbb{P}^1_{(x_0,x_1)}\times \mathbb{P}^{n}_{(w_1,\dots, w_{n+1}),} \end{align*} $$
$$ \begin{align*}Y_{(3,2)} = \left\{\sum_{i=0}^{3}x_0^{3-i}x_1^iB_i = 0\right\}\subset\mathbb{P}^1_{(x_0,x_1)}\times \mathbb{P}^{n}_{(w_1,\dots, w_{n+1}),} \end{align*} $$
where
![]() $B_0 = w_1L+A_1^0w_1^2$
,
$B_0 = w_1L+A_1^0w_1^2$
,
![]() $B_1 = Q+w_1A_1^1+w_1^2A_2^0$
,
$B_1 = Q+w_1A_1^1+w_1^2A_2^0$
,
![]() $B_{2} = A_{1}^2+w_1A_2^1$
,
$B_{2} = A_{1}^2+w_1A_2^1$
,
![]() $B_{3} = A_2^2$
, and
$B_{3} = A_2^2$
, and
![]() $L,A_i^1\in k[w_1,\dots ,w_{n+1}]_1$
,
$L,A_i^1\in k[w_1,\dots ,w_{n+1}]_1$
,
![]() $Q,A_i^2\in k[w_1,\dots ,w_{n+1}]_2$
,
$Q,A_i^2\in k[w_1,\dots ,w_{n+1}]_2$
,
![]() $A_i^0\in k$
for
$A_i^0\in k$
for
![]() $i = 1,2$
are general. If
$i = 1,2$
are general. If
![]() $n\geq 4$
, then
$n\geq 4$
, then
![]() $Y_{(3,2)}$
is unirational.
$Y_{(3,2)}$
is unirational.
Proof. Consider the rational map

where
![]() $\eta _i = B_ix_0^{2}+B_{i+1}x_0x_1+\dots +B_{3}x_0^{i-1}x_1^{3-i}$
for
$\eta _i = B_ix_0^{2}+B_{i+1}x_0x_1+\dots +B_{3}x_0^{i-1}x_1^{3-i}$
for
![]() $i = 1,2,3$
. By [Reference OttemOtt15, Theorem 1.1 (ii)] the rational map
$i = 1,2,3$
. By [Reference OttemOtt15, Theorem 1.1 (ii)] the rational map

yields a small transformation
, where
![]() $Y_{(3,2)}^{+}\subset \mathbb {P}^{2}_{(u_1,u_2,u_{3})}\times \mathbb {P}^{n}_{(w_1,\dots , w_{n+1})}$
is cut out by the minors of order three of the following matrix:
$Y_{(3,2)}^{+}\subset \mathbb {P}^{2}_{(u_1,u_2,u_{3})}\times \mathbb {P}^{n}_{(w_1,\dots , w_{n+1})}$
is cut out by the minors of order three of the following matrix:
 $$ \begin{align} M_{(u_1,u_2,u_{3})} = \left( \begin{array}{ccc} 0 & u_1 & B_0\\ -u_1 & u_2 & B_1\\ -u_{2} & u_{3} & B_{2}\\ -u_{3} & 0 & B_{3} \end{array} \right). \end{align} $$
$$ \begin{align} M_{(u_1,u_2,u_{3})} = \left( \begin{array}{ccc} 0 & u_1 & B_0\\ -u_1 & u_2 & B_1\\ -u_{2} & u_{3} & B_{2}\\ -u_{3} & 0 & B_{3} \end{array} \right). \end{align} $$
Consider the point
![]() $p = ([1:0],[0:\dots :0:1])\in Y_{(3,2)}$
, its image
$p = ([1:0],[0:\dots :0:1])\in Y_{(3,2)}$
, its image
 $$ \begin{align*}q &= ([B_1(0,\dots,0,1),B_{2}(0,\dots,0,1)],B_{3}(0,\dots,0,1)])\\ &= ([Q(0,\dots,0,1),A_{1}^2(0,\dots,0,1),A_{2}^2(0,\dots,0,1)]) \end{align*} $$
$$ \begin{align*}q &= ([B_1(0,\dots,0,1),B_{2}(0,\dots,0,1)],B_{3}(0,\dots,0,1)])\\ &= ([Q(0,\dots,0,1),A_{1}^2(0,\dots,0,1),A_{2}^2(0,\dots,0,1)]) \end{align*} $$
via
![]() $\eta $
and set
$\eta $
and set
![]() $\overline {u}_1 = Q(0,\dots ,0,1),\overline {u}_{2} = A_{1}^2(0,\dots ,0,1),\overline {u}_{3} = A_{2}^2(0,\dots ,0,1)$
. Let
$\overline {u}_1 = Q(0,\dots ,0,1),\overline {u}_{2} = A_{1}^2(0,\dots ,0,1),\overline {u}_{3} = A_{2}^2(0,\dots ,0,1)$
. Let
![]() $F_{\overline {u}}$
be the fiber of the first projection
$F_{\overline {u}}$
be the fiber of the first projection
![]() $\pi _1:\mathbb {P}^{2}_{(u_1,u_2,u_{3})}\times \mathbb {P}^{n}_{(w_1,\dots , w_{n+1})}\rightarrow \mathbb {P}^{2}_{(u_1,u_2,u_{3})}$
over
$\pi _1:\mathbb {P}^{2}_{(u_1,u_2,u_{3})}\times \mathbb {P}^{n}_{(w_1,\dots , w_{n+1})}\rightarrow \mathbb {P}^{2}_{(u_1,u_2,u_{3})}$
over
![]() $\overline {u} = [\overline {u}_1:\overline {u}_2:\overline {u}_{3}]$
. Then
$\overline {u} = [\overline {u}_1:\overline {u}_2:\overline {u}_{3}]$
. Then
is a complete intersection of two quadrics. Note that
![]() $q\in F_{\overline {u}}$
and since the
$q\in F_{\overline {u}}$
and since the
![]() $\overline {u}_i$
are general,
$\overline {u}_i$
are general,
![]() $F_{\overline {u}}$
is smooth. Therefore, if
$F_{\overline {u}}$
is smooth. Therefore, if
![]() $n\geq 4$
[Reference Colliot-Thélène, Sansuc and Swinnerton-DyerCTSSD87, Proposition 2.3] yields the unirationality of
$n\geq 4$
[Reference Colliot-Thélène, Sansuc and Swinnerton-DyerCTSSD87, Proposition 2.3] yields the unirationality of
![]() $F_{\overline {u}}$
. The strict transform of
$F_{\overline {u}}$
. The strict transform of
![]() $F_{\overline {u}}$
via
$F_{\overline {u}}$
via
![]() $\eta ^{+}$
is given by
$\eta ^{+}$
is given by
 $$ \begin{align*}\widetilde{F}_{\overline{u}} = \left\lbrace \operatorname{\mathrm{rank}}\left(\begin{array}{ccc} \overline{u}_1 & \overline{u}_2 & \overline{u}_3 \\ B_1x_0^2+B_2x_0x_1+B_3x_1^2 & B_2x_0^2+B_3x_0x_1 & B_3x_0^2 \end{array}\right) < 2\right\rbrace \subset \mathbb{P}^1_{(x_0,x_1)}\times \mathbb{P}^{n}_{(w_1,\dots, w_{n+1})}. \end{align*} $$
$$ \begin{align*}\widetilde{F}_{\overline{u}} = \left\lbrace \operatorname{\mathrm{rank}}\left(\begin{array}{ccc} \overline{u}_1 & \overline{u}_2 & \overline{u}_3 \\ B_1x_0^2+B_2x_0x_1+B_3x_1^2 & B_2x_0^2+B_3x_0x_1 & B_3x_0^2 \end{array}\right) < 2\right\rbrace \subset \mathbb{P}^1_{(x_0,x_1)}\times \mathbb{P}^{n}_{(w_1,\dots, w_{n+1})}. \end{align*} $$
So
![]() $\widetilde {F}_{\overline {u}}$
is unirational and maps dominantly onto
$\widetilde {F}_{\overline {u}}$
is unirational and maps dominantly onto
![]() $\mathbb {P}^1_{(x_0,x_1)}$
. Finally, to conclude it is enough to note that
$\mathbb {P}^1_{(x_0,x_1)}$
. Finally, to conclude it is enough to note that
![]() $Y_{(3,2)}\rightarrow \mathbb {P}^1_{(x_0,x_1)}$
is a fibration in quadric hypersurfaces and to apply Proposition 2.7 and Remark 2.8.
$Y_{(3,2)}\rightarrow \mathbb {P}^1_{(x_0,x_1)}$
is a fibration in quadric hypersurfaces and to apply Proposition 2.7 and Remark 2.8.
Proposition 3.13. Let
![]() $X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface having double points along a codimension two linear subspace
$X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface having double points along a codimension two linear subspace
![]() $\Lambda \subset \mathbb {P}^{n+1}$
, with a point
$\Lambda \subset \mathbb {P}^{n+1}$
, with a point
![]() $p\in X_4\setminus \Lambda $
and otherwise general. If
$p\in X_4\setminus \Lambda $
and otherwise general. If
![]() $n\geq 4$
, then
$n\geq 4$
, then
![]() $X_4$
is unirational.
$X_4$
is unirational.
Proof. The equation of
![]() $X_4\subset \mathbb {P}^{n+1}$
can be written as in Lemma 3.9 for
$X_4\subset \mathbb {P}^{n+1}$
can be written as in Lemma 3.9 for
![]() $d = 4$
. Hence, the claim follows from Lemma 3.9 and Proposition 3.10.
$d = 4$
. Hence, the claim follows from Lemma 3.9 and Proposition 3.10.
For quartic
![]() $3$
-folds, we have the following density result.
$3$
-folds, we have the following density result.
Proposition 3.14. Let
![]() $X_4\subset \mathbb {P}^{4}$
be a quartic hypersurface, over a number field k, having double points along a codimension two linear subspace
$X_4\subset \mathbb {P}^{4}$
be a quartic hypersurface, over a number field k, having double points along a codimension two linear subspace
![]() $\Lambda \subset \mathbb {P}^{4}$
, with a point
$\Lambda \subset \mathbb {P}^{4}$
, with a point
![]() $p\in X_4\setminus \Lambda $
and otherwise general. The set
$p\in X_4\setminus \Lambda $
and otherwise general. The set
![]() $X_4(k)$
of the k-rational points of
$X_4(k)$
of the k-rational points of
![]() $X_4$
is Zariski dense in
$X_4$
is Zariski dense in
![]() $X_4$
.
$X_4$
.
Proof. By Lemma 3.9, it is enough to prove that a general divisor
![]() $Y_{3,2}\subset \mathbb {P}^1\times \mathbb {P}^3$
as in Proposition 3.10 has dense k-points. Consider the
$Y_{3,2}\subset \mathbb {P}^1\times \mathbb {P}^3$
as in Proposition 3.10 has dense k-points. Consider the
![]() $2$
-plane
$2$
-plane
![]() $H = \{x_1 = w_1 = 0\}\subset Y_{3,2}$
and the rational map
$H = \{x_1 = w_1 = 0\}\subset Y_{3,2}$
and the rational map

induced by (3.11). Note that
![]() $\eta '$
maps H dominantly onto
$\eta '$
maps H dominantly onto
![]() $\mathbb {P}^{2}_{(u_1,u_2,u_{3})}$
. Take a general point
$\mathbb {P}^{2}_{(u_1,u_2,u_{3})}$
. Take a general point
![]() $p\in H$
, its image
$p\in H$
, its image
![]() $q = \eta '(p)$
and a general line
$q = \eta '(p)$
and a general line
![]() $L = \{\alpha _1u_1+\alpha _2u_2+\alpha _3u_3 = 0\}\subset \mathbb {P}^{2}_{(u_1,\dots ,u_{3})}$
through q. Set
$L = \{\alpha _1u_1+\alpha _2u_2+\alpha _3u_3 = 0\}\subset \mathbb {P}^{2}_{(u_1,\dots ,u_{3})}$
through q. Set
![]() $S_{L,p} = \eta ^{\prime -1}(L)$
. Since
$S_{L,p} = \eta ^{\prime -1}(L)$
. Since
![]() $Y_{(3,2)}$
is general
$Y_{(3,2)}$
is general
![]() $\eta '$
restricts to a morphism
$\eta '$
restricts to a morphism
![]() $\eta ^{\prime }_{|S_{L,p}}:S_{L,p}\rightarrow \mathbb {P}^1$
. A straightforward computation shows that
$\eta ^{\prime }_{|S_{L,p}}:S_{L,p}\rightarrow \mathbb {P}^1$
. A straightforward computation shows that
![]() $S_{L,p}$
is smooth, and by the argument in the second part of the proof of Proposition 3.10, the general fiber of
$S_{L,p}$
is smooth, and by the argument in the second part of the proof of Proposition 3.10, the general fiber of
![]() $\eta ^{\prime }_{|S_{L,p}}:S_{L,p}\rightarrow \mathbb {P}^1$
is a smooth curve of genus one.
$\eta ^{\prime }_{|S_{L,p}}:S_{L,p}\rightarrow \mathbb {P}^1$
is a smooth curve of genus one.
Furthermore,
![]() $C = H\cap S_{L,p} = \{\alpha _1B_1+\alpha _2B_2+\alpha _3B_3 = x_1 = w_1 = 0\}$
. Hence, since
$C = H\cap S_{L,p} = \{\alpha _1B_1+\alpha _2B_2+\alpha _3B_3 = x_1 = w_1 = 0\}$
. Hence, since
![]() $Y_{3,2}$
is general, C is a smooth conic with a point
$Y_{3,2}$
is general, C is a smooth conic with a point
![]() $p\in C$
. Note that a general fiber of
$p\in C$
. Note that a general fiber of
![]() $\eta ^{\prime }_{|S_{L,p}}:S_{L,p}\rightarrow \mathbb {P}^1$
intersects a general fiber of the quadric bundle
$\eta ^{\prime }_{|S_{L,p}}:S_{L,p}\rightarrow \mathbb {P}^1$
intersects a general fiber of the quadric bundle
![]() $Y_{3,2}\rightarrow \mathbb {P}^1$
in a zero-dimensional scheme of degree eight. So,
$Y_{3,2}\rightarrow \mathbb {P}^1$
in a zero-dimensional scheme of degree eight. So,
![]() $C\subset S_{L,p}$
is a rational
$C\subset S_{L,p}$
is a rational
![]() $4$
-section of
$4$
-section of
![]() $\eta ^{\prime }_{|S_{L,p}}$
.
$\eta ^{\prime }_{|S_{L,p}}$
.
Consider the fiber product
![]() $T = C\times _{L}S_{L,p}$
. Since
$T = C\times _{L}S_{L,p}$
. Since
![]() $p,L$
and
$p,L$
and
![]() $Y_{3,2}$
are general, the ramification divisor of
$Y_{3,2}$
are general, the ramification divisor of
![]() $\eta ^{\prime }_{|C}:C\rightarrow \mathbb {P}^1$
is disjoint from the singular fibers of
$\eta ^{\prime }_{|C}:C\rightarrow \mathbb {P}^1$
is disjoint from the singular fibers of
![]() $\eta ^{\prime }_{|S_{L,p}}$
. Hence, T is smooth and the proof of [Reference Harris and TschinkelHT00, Theorem 8.1] goes through. So the set
$\eta ^{\prime }_{|S_{L,p}}$
. Hence, T is smooth and the proof of [Reference Harris and TschinkelHT00, Theorem 8.1] goes through. So the set
![]() $S_{L,p}(k)$
of the k-rational points of
$S_{L,p}(k)$
of the k-rational points of
![]() $S_{L,p}$
is Zariski dense in
$S_{L,p}$
is Zariski dense in
![]() $S_{L,p}$
. Finally, letting the point p vary in H and the line L vary among the lines passing through
$S_{L,p}$
. Finally, letting the point p vary in H and the line L vary among the lines passing through
![]() $q = \eta '(p)$
we get the claim.
$q = \eta '(p)$
we get the claim.
The following is our main result on the unirationality of quadric hypersurfaces having double points along a linear subspace.
Theorem 3.15. Let
![]() $X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface having double points along an h-plane
$X_4\subset \mathbb {P}^{n+1}$
be a quartic hypersurface having double points along an h-plane
![]() $\Lambda \subset \mathbb {P}^{n+1}$
, with a point
$\Lambda \subset \mathbb {P}^{n+1}$
, with a point
![]() $p\in X_4\setminus \Lambda $
and otherwise general. If
$p\in X_4\setminus \Lambda $
and otherwise general. If
![]() $n\geq 4$
and
$n\geq 4$
and
![]() $h\geq 3$
, then
$h\geq 3$
, then
![]() $X_4$
is unirational.
$X_4$
is unirational.
Furthermore, if k is a
![]() $C_r$
field,
$C_r$
field,
![]() $n\geq 3$
, and
$n\geq 3$
, and
![]() $s+1> 2^r$
, where
$s+1> 2^r$
, where
![]() $s = \max \{n-h,h\}$
a general quartic hypersurface
$s = \max \{n-h,h\}$
a general quartic hypersurface
![]() $X_4\subset \mathbb {P}^{n+1}$
having double points along an h-plane is unirational.
$X_4\subset \mathbb {P}^{n+1}$
having double points along an h-plane is unirational.
Proof. The case
![]() $h = n-1$
comes from Proposition 3.13. Let
$h = n-1$
comes from Proposition 3.13. Let
![]() be the projection from
be the projection from
![]() $H = \left \langle p,\Lambda \right \rangle $
,
$H = \left \langle p,\Lambda \right \rangle $
,
![]() $\widetilde {\pi }_{H}:\widetilde {X}_4\rightarrow \mathbb {P}^{n-h-1}$
, and
$\widetilde {\pi }_{H}:\widetilde {X}_4\rightarrow \mathbb {P}^{n-h-1}$
, and
![]() $F_p\cong \mathbb {P}^{n-h-1}$
the fiber over p of the blowup
$F_p\cong \mathbb {P}^{n-h-1}$
the fiber over p of the blowup
![]() $\widetilde {X}_4\rightarrow X_4$
along
$\widetilde {X}_4\rightarrow X_4$
along
![]() $H\cap X_4$
. Note that since
$H\cap X_4$
. Note that since
![]() $X_4$
is irreducible the blowup
$X_4$
is irreducible the blowup
![]() $\widetilde {X}_4$
is also irreducible.
$\widetilde {X}_4$
is also irreducible.
The generic fiber
![]() $\widetilde {X}_{4,\eta }$
of
$\widetilde {X}_{4,\eta }$
of
![]() $\widetilde {\pi }_{H}:\widetilde {X}_4\rightarrow \mathbb {P}^{n-h-1}$
is a quartic hypersurface
$\widetilde {\pi }_{H}:\widetilde {X}_4\rightarrow \mathbb {P}^{n-h-1}$
is a quartic hypersurface
![]() $\widetilde {X}_{4,\eta }\subset \mathbb {P}^{h+2}_{k(t_1,\dots ,t_{n-h-1})}$
with double points along an h-plane and with a
$\widetilde {X}_{4,\eta }\subset \mathbb {P}^{h+2}_{k(t_1,\dots ,t_{n-h-1})}$
with double points along an h-plane and with a
![]() $k(t_1,\dots ,t_{n-h-1})$
-rational point induced by
$k(t_1,\dots ,t_{n-h-1})$
-rational point induced by
![]() $F_p$
.
$F_p$
.
Therefore, Proposition 3.13 yields that
![]() $\widetilde {X}_{4,\eta }$
is unirational over
$\widetilde {X}_{4,\eta }$
is unirational over
![]() $k(t_1,\dots ,t_{n-h-1})$
and since
$k(t_1,\dots ,t_{n-h-1})$
and since
![]() $\widetilde {X}_4$
is irreducible
$\widetilde {X}_4$
is irreducible
![]() $\widetilde {X}_4$
is unirational.
$\widetilde {X}_4$
is unirational.
Now, assume k to be
![]() $C_r$
. The exceptional divisor
$C_r$
. The exceptional divisor
![]() $\widetilde {E}$
in Lemma 2.4 is a divisor of bidegree
$\widetilde {E}$
in Lemma 2.4 is a divisor of bidegree
![]() $(2,2)$
in
$(2,2)$
in
![]() $\mathbb {P}^{n-h}\times \mathbb {P}^h$
, and since
$\mathbb {P}^{n-h}\times \mathbb {P}^h$
, and since
![]() $X_4$
is general
$X_4$
is general
![]() $\widetilde {E}$
maps dominantly onto
$\widetilde {E}$
maps dominantly onto
![]() $\mathbb {P}^{n-h}$
. Furthermore, since both the fibrations on
$\mathbb {P}^{n-h}$
. Furthermore, since both the fibrations on
![]() $\widetilde {E}$
have quadric hypersurfaces as fibers and
$\widetilde {E}$
have quadric hypersurfaces as fibers and
![]() $s+1> 2^r$
by Remark 2.10 the divisor
$s+1> 2^r$
by Remark 2.10 the divisor
![]() $\widetilde {E}$
has a point. To conclude, it is enough to apply [Reference MassarentiMas22, Theorem 1.8] and Proposition 2.7.
$\widetilde {E}$
has a point. To conclude, it is enough to apply [Reference MassarentiMas22, Theorem 1.8] and Proposition 2.7.
Remark 3.16. In the second part of Theorem 3.15, the assumption on the base field is needed in order to ensure the existence of a point in the exceptional divisor
![]() $\widetilde {E}\subset \mathbb {P}^{n-h}\times \mathbb {P}^h$
. Indeed, over non
$\widetilde {E}\subset \mathbb {P}^{n-h}\times \mathbb {P}^h$
. Indeed, over non
![]() $C_r$
fields there are divisors of bidegree
$C_r$
fields there are divisors of bidegree
![]() $(2,2)$
in
$(2,2)$
in
![]() $\mathbb {P}^{n-h}\times \mathbb {P}^h$
without points [Reference MassarentiMas22, Remark 4.15].
$\mathbb {P}^{n-h}\times \mathbb {P}^h$
without points [Reference MassarentiMas22, Remark 4.15].
Remark 3.17. In Theorem 3.15, the assumption on the existence of a point in
![]() $X_4\setminus \Lambda $
is necessary as the following argument shows. Take, for instance,
$X_4\setminus \Lambda $
is necessary as the following argument shows. Take, for instance,
![]() $n = 3$
,
$n = 3$
,
![]() $h = 1$
and
$h = 1$
and
![]() $k = \mathbb {R}$
. By Lemma 2.4,
$k = \mathbb {R}$
. By Lemma 2.4,
![]() $X_4$
is birational to a conic bundle
$X_4$
is birational to a conic bundle
![]() $D\subset \mathcal {T}_{1,0,0}$
of multidegree
$D\subset \mathcal {T}_{1,0,0}$
of multidegree
![]() $(4,3,3,2,2,2)$
. We may write D as the zero set of a polynomial
$(4,3,3,2,2,2)$
. We may write D as the zero set of a polynomial
where
![]() $a_i\in \mathbb {R}[x_1,x_2,y_0,y_1,y_2]$
. Let V be the
$a_i\in \mathbb {R}[x_1,x_2,y_0,y_1,y_2]$
. Let V be the
![]() $\mathbb {R}$
-vector space parametrizing these conic bundles and consider the map
$\mathbb {R}$
-vector space parametrizing these conic bundles and consider the map
 $$ \begin{align*}\begin{array}{cccc} ev: & V\times\mathbb{R}^5 & \longrightarrow & \mathbb{R}^5 \\ & (f,(\overline{x}_1,\overline{x}_2,\overline{y}_0,\overline{y}_1,\overline{y}_2)) & \mapsto & P_{f,\overline{x}_1,\overline{x}_2,\overline{y}_0,\overline{y}_1,\overline{y}_2}(x_0), \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{cccc} ev: & V\times\mathbb{R}^5 & \longrightarrow & \mathbb{R}^5 \\ & (f,(\overline{x}_1,\overline{x}_2,\overline{y}_0,\overline{y}_1,\overline{y}_2)) & \mapsto & P_{f,\overline{x}_1,\overline{x}_2,\overline{y}_0,\overline{y}_1,\overline{y}_2}(x_0), \end{array} \end{align*} $$
where
![]() $P_{f,\overline {x}_1,\overline {x}_2,\overline {y}_0,\overline {y}_1,\overline {y}_2}(x_0) = f(x_0,\overline {x}_1,\overline {x}_2,\overline {y}_0,\overline {y}_1,\overline {y}_2)\in \mathbb {R}[x_0]$
. The polynomials
$P_{f,\overline {x}_1,\overline {x}_2,\overline {y}_0,\overline {y}_1,\overline {y}_2}(x_0) = f(x_0,\overline {x}_1,\overline {x}_2,\overline {y}_0,\overline {y}_1,\overline {y}_2)\in \mathbb {R}[x_0]$
. The polynomials
![]() $P_{f,\overline {x}_1,\overline {x}_2,\overline {y}_0,\overline {y}_1,\overline {y}_2}(x_0)$
with a real root form a semialgebraic subset
$P_{f,\overline {x}_1,\overline {x}_2,\overline {y}_0,\overline {y}_1,\overline {y}_2}(x_0)$
with a real root form a semialgebraic subset
![]() $R_{rr}\subset \mathbb {R}^5$
of maximal dimension; see, for instance, [Reference Basu, Pollack and RoyBPR06, Section 4.2.3]. Hence,
$R_{rr}\subset \mathbb {R}^5$
of maximal dimension; see, for instance, [Reference Basu, Pollack and RoyBPR06, Section 4.2.3]. Hence,
![]() $ev^{-1}(R_{rr})\subset V\times \mathbb {R}^5$
is also a semialgebraic subset of maximal dimension and then the Tarski–Seidenberg principle [Reference Bochnak, Coste and RoyBCR98, Section 2.2] yields that
$ev^{-1}(R_{rr})\subset V\times \mathbb {R}^5$
is also a semialgebraic subset of maximal dimension and then the Tarski–Seidenberg principle [Reference Bochnak, Coste and RoyBCR98, Section 2.2] yields that
![]() $Z_{rp}= \pi _1(ev^{-1}(R_{rr}))\subset V$
, where
$Z_{rp}= \pi _1(ev^{-1}(R_{rr}))\subset V$
, where
![]() $\pi _1:V\times \mathbb {R}^5\rightarrow V$
is the projection, is a semialgebraic subset of maximal dimension. Note that
$\pi _1:V\times \mathbb {R}^5\rightarrow V$
is the projection, is a semialgebraic subset of maximal dimension. Note that
The complementary set
![]() $Z_{nrp} = Z_{rp}^c$
is nonempty, take, for instance,
$Z_{nrp} = Z_{rp}^c$
is nonempty, take, for instance,
Hence,
![]() $Z_{nrp}\subset V$
is also a semialgebraic subset of maximal dimension. By Lemma 2.4, the quartics
$Z_{nrp}\subset V$
is also a semialgebraic subset of maximal dimension. By Lemma 2.4, the quartics
![]() $X_4\subset \mathbb {P}^4$
corresponding to the conic bundles in
$X_4\subset \mathbb {P}^4$
corresponding to the conic bundles in
![]() $Z_{nrp}$
do not have a point in
$Z_{nrp}$
do not have a point in
![]() $X_4\setminus \Lambda $
, and hence, they cannot be unirational.
$X_4\setminus \Lambda $
, and hence, they cannot be unirational.
Lemma 3.18. Consider the hypersurface
where
![]() $A_i = A_i^2 + z_0A_i^1+z_0^2A_i^0$
, and
$A_i = A_i^2 + z_0A_i^1+z_0^2A_i^0$
, and
![]() $A_i^1\in k[z_1,\dots ,z_{n+1}]_1$
,
$A_i^1\in k[z_1,\dots ,z_{n+1}]_1$
,
![]() $Q,A_i^2\in k[z_1,\dots ,z_{n+1}]_2$
,
$Q,A_i^2\in k[z_1,\dots ,z_{n+1}]_2$
,
![]() $A_i^0\in k$
for
$A_i^0\in k$
for
![]() $i = 1,\dots ,d-2$
. Then
$i = 1,\dots ,d-2$
. Then
![]() $X_d$
is birational to the divisor
$X_d$
is birational to the divisor
 $$ \begin{align*}Y_{(d-2,2)} = \left\{ x_0^{d-2}Q+\sum_{i=1}^{d-2}x_0^{d-2-i}x_1^iA_i = 0\right\}\subset\mathbb{P}^1_{(x_0,x_1)}\times \mathbb{P}^{n}_{(z_1,\dots, z_{n+1})} \end{align*} $$
$$ \begin{align*}Y_{(d-2,2)} = \left\{ x_0^{d-2}Q+\sum_{i=1}^{d-2}x_0^{d-2-i}x_1^iA_i = 0\right\}\subset\mathbb{P}^1_{(x_0,x_1)}\times \mathbb{P}^{n}_{(z_1,\dots, z_{n+1})} \end{align*} $$
of bidegree
![]() $(d-2,2)$
.
$(d-2,2)$
.
Proof. It is enough to substitute
![]() $z_0 = \frac {x_0}{x_1}z_1$
in the equation of
$z_0 = \frac {x_0}{x_1}z_1$
in the equation of
![]() $X_d$
and to clear the denominators of the resulting polynomial.
$X_d$
and to clear the denominators of the resulting polynomial.
For quartic hypersurfaces with a double point, we get a version of Theorem 3.15 with a slightly less restrictive condition on n.
Proposition 3.19. Let
![]() $X_d\subset \mathbb {P}^{n+1}$
be a hypersurface of degree d having multiplicity
$X_d\subset \mathbb {P}^{n+1}$
be a hypersurface of degree d having multiplicity
![]() $d-2$
along a codimension two linear subspace
$d-2$
along a codimension two linear subspace
![]() $\Lambda \subset \mathbb {P}^{n+1}$
, with a point
$\Lambda \subset \mathbb {P}^{n+1}$
, with a point
![]() $p\in X_d\setminus \Lambda $
, a double point
$p\in X_d\setminus \Lambda $
, a double point
![]() $q\in X_d\setminus \Lambda $
and otherwise general. If either
$q\in X_d\setminus \Lambda $
and otherwise general. If either
![]() $d = 4$
and
$d = 4$
and
![]() $n\geq 2$
or
$n\geq 2$
or
![]() $d = 5$
and
$d = 5$
and
![]() $n\geq 4$
, then
$n\geq 4$
, then
![]() $X_d$
is unirational.
$X_d$
is unirational.
Proof. We may assume that
![]() $\Lambda = \{z_0 = z_1 = 0\}$
and
$\Lambda = \{z_0 = z_1 = 0\}$
and
![]() $q = [1:0:\dots :0]$
so that the equation of
$q = [1:0:\dots :0]$
so that the equation of
![]() $X_d\subset \mathbb {P}^{n+1}$
can be written as in Lemma 3.18. First, consider the case
$X_d\subset \mathbb {P}^{n+1}$
can be written as in Lemma 3.18. First, consider the case
![]() $d = 4$
. By Lemma 3.18
$d = 4$
. By Lemma 3.18
![]() $X_4$
is birational to a divisor
$X_4$
is birational to a divisor
![]() $Y_{(2,2)}\subset \mathbb {P}^1_{(x_0,x_1)}\times \mathbb {P}^{n}_{(z_1,\dots , z_{n+1})}$
of bidegree
$Y_{(2,2)}\subset \mathbb {P}^1_{(x_0,x_1)}\times \mathbb {P}^{n}_{(z_1,\dots , z_{n+1})}$
of bidegree
![]() $(2,2)$
. The point
$(2,2)$
. The point
![]() $p\in X_d\setminus \Lambda $
yields a point
$p\in X_d\setminus \Lambda $
yields a point
![]() $p'\in Y_{(2,2)}$
. Let H be a general
$p'\in Y_{(2,2)}$
. Let H be a general
![]() $2$
-plane in
$2$
-plane in
![]() $\mathbb {P}^{n}_{(z_1,\dots , z_{n+1})}$
through the projection of
$\mathbb {P}^{n}_{(z_1,\dots , z_{n+1})}$
through the projection of
![]() $p'$
and set
$p'$
and set
![]() $\Gamma = \mathbb {P}^1_{(x_0,x_1)}\times H$
. Then
$\Gamma = \mathbb {P}^1_{(x_0,x_1)}\times H$
. Then
![]() $W = Y_{(2,2)}\cap \Gamma $
is a divisor of bidegree
$W = Y_{(2,2)}\cap \Gamma $
is a divisor of bidegree
![]() $(2,2)$
in
$(2,2)$
in
![]() $\mathbb {P}^1_{(x_0,x_1)} \times \mathbb {P}^2$
which by [Reference Kollár and MellaKM17, Corollary 8] is unirational. Since W maps dominantly onto
$\mathbb {P}^1_{(x_0,x_1)} \times \mathbb {P}^2$
which by [Reference Kollár and MellaKM17, Corollary 8] is unirational. Since W maps dominantly onto
![]() $\mathbb {P}^1_{(x_0,x_1)}$
, to conclude it is enough to apply Proposition 2.7.
$\mathbb {P}^1_{(x_0,x_1)}$
, to conclude it is enough to apply Proposition 2.7.
Now, let
![]() $d = 5$
. Then by Lemma 3.18
$d = 5$
. Then by Lemma 3.18
![]() $X_5$
is birational to a divisor
$X_5$
is birational to a divisor
![]() $Y_{(3,2)}\subset \mathbb {P}^1_{(x_0,x_1)}\times \mathbb {P}^{n}_{(z_1,\dots , z_{n+1})}$
of bidegree
$Y_{(3,2)}\subset \mathbb {P}^1_{(x_0,x_1)}\times \mathbb {P}^{n}_{(z_1,\dots , z_{n+1})}$
of bidegree
![]() $(3,2)$
. This divisor is not of the same form of those considered in Proposition 3.10. However, the argument in the proof of Proposition 3.10 goes through smoothly and shows
$(3,2)$
. This divisor is not of the same form of those considered in Proposition 3.10. However, the argument in the proof of Proposition 3.10 goes through smoothly and shows
![]() $Y_{(3,2)}$
is unirational.
$Y_{(3,2)}$
is unirational.
Remark 3.20. The argument in the proof of Proposition 3.10 works indeed for a general divisor of bidegree
![]() $(3,2)$
as shown in [Reference MassarentiMas22, Proposition 3.2] which works for a divisor of bidegree
$(3,2)$
as shown in [Reference MassarentiMas22, Proposition 3.2] which works for a divisor of bidegree
![]() $(3,2)$
in
$(3,2)$
in
![]() $\mathbb {P}^1\times \mathbb {P}^n$
with a point and otherwise general. So [Reference MassarentiMas22, Proposition 3.2] cannot be applied directly to the divisors
$\mathbb {P}^1\times \mathbb {P}^n$
with a point and otherwise general. So [Reference MassarentiMas22, Proposition 3.2] cannot be applied directly to the divisors
![]() $Y_{(3,2)}$
in Proposition 3.10 which are special. In the proof of Proposition 3.10, it is shown that the argument in the proof of [Reference MassarentiMas22, Proposition 3.2] works for a general
$Y_{(3,2)}$
in Proposition 3.10 which are special. In the proof of Proposition 3.10, it is shown that the argument in the proof of [Reference MassarentiMas22, Proposition 3.2] works for a general
![]() $Y_{(3,2)}$
, in other words that a general divisor of the form
$Y_{(3,2)}$
, in other words that a general divisor of the form
![]() $Y_{(3,2)}$
is general enough, among the divisor of bidegree
$Y_{(3,2)}$
is general enough, among the divisor of bidegree
![]() $(3,2)$
in
$(3,2)$
in
![]() $\mathbb {P}^1\times \mathbb {P}^n$
, for [Reference MassarentiMas22, Proposition 3.2] to apply.
$\mathbb {P}^1\times \mathbb {P}^n$
, for [Reference MassarentiMas22, Proposition 3.2] to apply.
Lemma 3.21. Let
![]() $D\subset \mathbb {P}^{n-h}\times \mathbb {P}^h$
be an irreducible divisor of bidegree
$D\subset \mathbb {P}^{n-h}\times \mathbb {P}^h$
be an irreducible divisor of bidegree
![]() $(1,a)$
. Then D is rational.
$(1,a)$
. Then D is rational.
Proof. If
![]() $n-h = 1$
, then the projection
$n-h = 1$
, then the projection
![]() $\pi _{2|D}:D\rightarrow \mathbb {P}^h$
is birational. Assume
$\pi _{2|D}:D\rightarrow \mathbb {P}^h$
is birational. Assume
![]() $n-h\geq 2$
. The generic fiber of
$n-h\geq 2$
. The generic fiber of
![]() $\pi _{2|D}:D\rightarrow \mathbb {P}^h$
is an
$\pi _{2|D}:D\rightarrow \mathbb {P}^h$
is an
![]() $(n-h-1)$
-dimensional projective space over the function field of
$(n-h-1)$
-dimensional projective space over the function field of
![]() $\mathbb {P}^h$
. So we can find an open subset
$\mathbb {P}^h$
. So we can find an open subset
![]() $U\subset \mathbb {P}^h$
such that
$U\subset \mathbb {P}^h$
such that
![]() $\pi _{2|D}^{-1}(U)$
is birational to
$\pi _{2|D}^{-1}(U)$
is birational to
![]() $U\times \mathbb {P}^{n-h-1}$
. Finally, since D is irreducible we conclude that D is rational.
$U\times \mathbb {P}^{n-h-1}$
. Finally, since D is irreducible we conclude that D is rational.
The following is our main result on the unirationality of quartic hypersurface containing a linear subspace.
Theorem 3.22. Let
![]() $X_4\subset \mathbb {P}^{n+1}$
be an irreducible quartic hypersurface containing an h-plane
$X_4\subset \mathbb {P}^{n+1}$
be an irreducible quartic hypersurface containing an h-plane
![]() $\Lambda \subset \mathbb {P}^{n+1}$
. Assume that
$\Lambda \subset \mathbb {P}^{n+1}$
. Assume that
![]() $\Lambda \cap \operatorname {\mathrm {Sing}}(X_4)$
has dimension at most
$\Lambda \cap \operatorname {\mathrm {Sing}}(X_4)$
has dimension at most
![]() $h-2$
and that
$h-2$
and that
![]() $X_4$
is not a cone over a quartic of smaller dimension. If
$X_4$
is not a cone over a quartic of smaller dimension. If
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $h\geq 2$
, then
$h\geq 2$
, then
![]() $X_4$
is unirational.
$X_4$
is unirational.
Proof. Consider the blowup
![]() $\widetilde {X}_4$
along
$\widetilde {X}_4$
along
![]() $\Lambda $
in Lemma 2.4. Under our hypotheses,
$\Lambda $
in Lemma 2.4. Under our hypotheses,
![]() $X_4$
cannot be singular at the general point of
$X_4$
cannot be singular at the general point of
![]() $\Lambda $
. So the exceptional divisor
$\Lambda $
. So the exceptional divisor
![]() $\widetilde {E}\subset \mathbb {P}^{n-h}\times \mathbb {P}^h$
has bidegree
$\widetilde {E}\subset \mathbb {P}^{n-h}\times \mathbb {P}^h$
has bidegree
![]() $(1,3)$
, and Lemma 3.21 yields that
$(1,3)$
, and Lemma 3.21 yields that
![]() $\widetilde {E}$
is unirational. The projection
$\widetilde {E}$
is unirational. The projection
![]() $\pi :\widetilde {X}_4\rightarrow \mathbb {P}^{n-h}$
is a fibration in h-dimensional cubic hypersurfaces. Therefore, thanks to Proposition 2.7 and Remark 2.8 to conclude it is enough to show that
$\pi :\widetilde {X}_4\rightarrow \mathbb {P}^{n-h}$
is a fibration in h-dimensional cubic hypersurfaces. Therefore, thanks to Proposition 2.7 and Remark 2.8 to conclude it is enough to show that
![]() $\pi _{|\widetilde {E}}:\widetilde {E}\rightarrow \mathbb {P}^{n-h}$
is dominant.
$\pi _{|\widetilde {E}}:\widetilde {E}\rightarrow \mathbb {P}^{n-h}$
is dominant.
Since
![]() $X_4$
is not a cone over a quartic of smaller dimension by the expression of
$X_4$
is not a cone over a quartic of smaller dimension by the expression of
![]() $\widetilde {X}_4$
in (2.6), we see that
$\widetilde {X}_4$
in (2.6), we see that
![]() $\pi _{|\widetilde {E}}:\widetilde {E}\rightarrow \mathbb {P}^{n-h}$
is not dominant if and only if the equation of
$\pi _{|\widetilde {E}}:\widetilde {E}\rightarrow \mathbb {P}^{n-h}$
is not dominant if and only if the equation of
![]() $X_d$
is of the following form
$X_d$
is of the following form
 $$ \begin{align*}X_d = \left\{\sum_{i=0}^{n-h}z_i(C_i(z_0,\dots,z_{n-h})+c_iP) = 0\right\}\subset\mathbb{P}^{n+1}, \end{align*} $$
$$ \begin{align*}X_d = \left\{\sum_{i=0}^{n-h}z_i(C_i(z_0,\dots,z_{n-h})+c_iP) = 0\right\}\subset\mathbb{P}^{n+1}, \end{align*} $$
where
![]() $C_i\in k[z_0,\dots ,z_{n-h}]_{d-1}$
,
$C_i\in k[z_0,\dots ,z_{n-h}]_{d-1}$
,
![]() $c_i\in k$
and
$c_i\in k$
and
![]() $P\in k[z_0,\dots ,z_{n+1}]_{d-1}$
. In particular,
$P\in k[z_0,\dots ,z_{n+1}]_{d-1}$
. In particular,
and since
![]() $\dim (Z)\geq h-1$
we get a contradiction.
$\dim (Z)\geq h-1$
we get a contradiction.
Corollary 3.23. Assume that
![]() $h\geq 2$
,
$h\geq 2$
,
![]() $n> 2h-1$
, and let
$n> 2h-1$
, and let
![]() $X_4\subset \mathbb {P}^{n+1}$
be a general quartic hypersurface containing an h-plane. Then
$X_4\subset \mathbb {P}^{n+1}$
be a general quartic hypersurface containing an h-plane. Then
![]() $X_4$
is unirational.
$X_4$
is unirational.
Proof. Note that
![]() $n> 2h-1$
yields that a general quartic containing a fixed h-plane is smooth. The claim follows from Theorem 3.22.
$n> 2h-1$
yields that a general quartic containing a fixed h-plane is smooth. The claim follows from Theorem 3.22.
4 Divisors in products of projective spaces and Quintics
We now study the unirationality of quintic hypersurfaces that are singular along linear subspaces and of divisors of bidegree
![]() $(3,2)$
in products of projective spaces. We begin with a series of preliminary results that we will need later on.
$(3,2)$
in products of projective spaces. We begin with a series of preliminary results that we will need later on.
Lemma 4.1. Let
![]() $\mathcal {C}\rightarrow W$
be a fibration in m-dimensional cubic hypersurfaces with
$\mathcal {C}\rightarrow W$
be a fibration in m-dimensional cubic hypersurfaces with
![]() $m\geq 2$
,
$m\geq 2$
,
![]() $\mathcal {C}$
irreducible and W a rational variety over a
$\mathcal {C}$
irreducible and W a rational variety over a
![]() $C_r$
field k. If the general fiber of
$C_r$
field k. If the general fiber of
![]() $\mathcal {C}\rightarrow W$
is an irreducible cubic with no triple point and
$\mathcal {C}\rightarrow W$
is an irreducible cubic with no triple point and
then
![]() $\mathcal {C}$
is unirational.
$\mathcal {C}$
is unirational.
Proof. Let
![]() $\mathcal {C}'$
be the generic fiber of
$\mathcal {C}'$
be the generic fiber of
![]() $\mathcal {C}\rightarrow W$
. Then
$\mathcal {C}\rightarrow W$
. Then
![]() $\mathcal {C}'$
is a cubic hypersurface over the function field
$\mathcal {C}'$
is a cubic hypersurface over the function field
![]() $F = k(t_1,\dots ,t_{\dim (W)})$
. Since
$F = k(t_1,\dots ,t_{\dim (W)})$
. Since
![]() $m+2> 3^{r+\dim (W)}$
, Remark 2.10 yields that
$m+2> 3^{r+\dim (W)}$
, Remark 2.10 yields that
![]() $\mathcal {C}'$
has a point. Hence, by [Reference KollárKol02, Theorem 1]
$\mathcal {C}'$
has a point. Hence, by [Reference KollárKol02, Theorem 1]
![]() $\mathcal {C}'$
is unirational over F and so since
$\mathcal {C}'$
is unirational over F and so since
![]() $\mathcal {C}$
is irreducible
$\mathcal {C}$
is irreducible
![]() $\mathcal {C}$
is unirational.
$\mathcal {C}$
is unirational.
Lemma 4.2. Let
![]() $Q^{N-1}\subset \mathbb {P}^{N}$
be a smooth
$Q^{N-1}\subset \mathbb {P}^{N}$
be a smooth
![]() $(N-1)$
-dimensional quadric hypersurface over a
$(N-1)$
-dimensional quadric hypersurface over a
![]() $C_r$
field. If
$C_r$
field. If
for some
![]() $0\leq s \leq \lfloor \frac {N-1}{2}\rfloor $
, then through any point of
$0\leq s \leq \lfloor \frac {N-1}{2}\rfloor $
, then through any point of
![]() $Q^{N-1}$
there is an s-plane contained in
$Q^{N-1}$
there is an s-plane contained in
![]() $Q^{N-1}$
.
$Q^{N-1}$
.
Proof. Since
![]() $N-1> 2^r - 2$
by Remark 2.10
$N-1> 2^r - 2$
by Remark 2.10
![]() $Q^{N-1}$
has a point. Hence,
$Q^{N-1}$
has a point. Hence,
![]() $Q^{N-1}$
is rational and in particular the set of its rational points is dense. Take a point
$Q^{N-1}$
is rational and in particular the set of its rational points is dense. Take a point
![]() $x_0 \in Q^{N-1}$
.
$x_0 \in Q^{N-1}$
.
The tangent space
![]() $T_{x_0}Q^{N-1}$
cuts out on
$T_{x_0}Q^{N-1}$
cuts out on
![]() $Q^{N-1}$
a cone with vertex
$Q^{N-1}$
a cone with vertex
![]() $x_0$
over an
$x_0$
over an
![]() $(N-3)$
-dimensional quadric
$(N-3)$
-dimensional quadric
![]() $Q^{N-3}$
. Since
$Q^{N-3}$
. Since
![]() $N-3> 2^r - 2$
Remark 2.10 yields the existence of a point
$N-3> 2^r - 2$
Remark 2.10 yields the existence of a point
![]() $x_1 \in Q^{N-3}$
. The line
$x_1 \in Q^{N-3}$
. The line
![]() $\left \langle x_0,x_1\right \rangle $
is therefore contained in
$\left \langle x_0,x_1\right \rangle $
is therefore contained in
![]() $Q^{N-1}$
.
$Q^{N-1}$
.
Now,
![]() $T_{x_1}Q^{N-3}\cap Q^{N-3}$
is a cone with vertex
$T_{x_1}Q^{N-3}\cap Q^{N-3}$
is a cone with vertex
![]() $x_1$
over an
$x_1$
over an
![]() $(N-5)$
-dimensional quadric
$(N-5)$
-dimensional quadric
![]() $Q^{N-5}$
which again by Remark 2.10 has a point
$Q^{N-5}$
which again by Remark 2.10 has a point
![]() $x_2\in Q^{N-5}$
. The
$x_2\in Q^{N-5}$
. The
![]() $2$
-plane
$2$
-plane
![]() $\left \langle x_0,x_1,x_2\right \rangle $
is contained in
$\left \langle x_0,x_1,x_2\right \rangle $
is contained in
![]() $Q^{N-1}$
.
$Q^{N-1}$
.
Proceeding recursively, we have that
![]() $T_{x_{s-1}}Q^{N-2(s-1)-1}\cap Q^{N-2(s-1)-1}$
is a cone with vertex
$T_{x_{s-1}}Q^{N-2(s-1)-1}\cap Q^{N-2(s-1)-1}$
is a cone with vertex
![]() $x_{s-1}$
over an
$x_{s-1}$
over an
![]() $(N-2s-1)$
-dimensional quadric
$(N-2s-1)$
-dimensional quadric
![]() $Q^{N-2s-1}$
. Since
$Q^{N-2s-1}$
. Since
![]() $N-2s+1> 2^r$
, the quadric
$N-2s+1> 2^r$
, the quadric
![]() $Q^{N-2s-1}$
has a point
$Q^{N-2s-1}$
has a point
![]() $x_s$
and the s-plane
$x_s$
and the s-plane
![]() $\left \langle x_0,\dots ,x_s\right \rangle $
is then contained in
$\left \langle x_0,\dots ,x_s\right \rangle $
is then contained in
![]() $Q^{N-1}$
.
$Q^{N-1}$
.
Lemma 4.3. Let
![]() $X = Q_1\cap \dots \cap Q_c\subset \mathbb {P}^N$
be a smooth complete intersection of quadrics. Assume that X contains a
$X = Q_1\cap \dots \cap Q_c\subset \mathbb {P}^N$
be a smooth complete intersection of quadrics. Assume that X contains a
![]() $(c-1)$
-plane
$(c-1)$
-plane
![]() $\Lambda $
. Then X is rational.
$\Lambda $
. Then X is rational.
Proof. Note that since X is smooth
![]() $Q_i$
must be smooth along X. Let H be a general c-plane containing
$Q_i$
must be smooth along X. Let H be a general c-plane containing
![]() $\Lambda $
. Then H intersects
$\Lambda $
. Then H intersects
![]() $Q_i$
along
$Q_i$
along
![]() $\Lambda \cup H_i$
where
$\Lambda \cup H_i$
where
![]() $H_i$
is a
$H_i$
is a
![]() $(c-1)$
-plane. Hence, we get c linear subspaces of dimension
$(c-1)$
-plane. Hence, we get c linear subspaces of dimension
![]() $c-1$
of
$c-1$
of
![]() $H\cong \mathbb {P}^c$
.
$H\cong \mathbb {P}^c$
.
Since H is general, these
![]() $(c-1)$
-planes intersect in a point
$(c-1)$
-planes intersect in a point
![]() $x_H = H_1\cap \dots \cap H_c \in X$
. To conclude, it is enough to parametrize X with the
$x_H = H_1\cap \dots \cap H_c \in X$
. To conclude, it is enough to parametrize X with the
![]() $\mathbb {P}^{N-c}$
of c-planes containing
$\mathbb {P}^{N-c}$
of c-planes containing
![]() $\Lambda $
.
$\Lambda $
.
Proposition 4.4. Let
![]() $X = Q_1\cap \dots \cap Q_c\subset \mathbb {P}^{N}$
be a smooth complete intersection of quadrics over a
$X = Q_1\cap \dots \cap Q_c\subset \mathbb {P}^{N}$
be a smooth complete intersection of quadrics over a
![]() $C_r$
field. If
$C_r$
field. If
then through any point of X there is an s-plane contained in X.
Proof. For
![]() $s = 0$
, the claim follows from Remark 2.10. We proceed by induction on s. Since
$s = 0$
, the claim follows from Remark 2.10. We proceed by induction on s. Since
through any point of X, there is an
![]() $(s-1)$
-plane. Fix one of these
$(s-1)$
-plane. Fix one of these
![]() $(s-1)$
-planes, and denote it by
$(s-1)$
-planes, and denote it by
![]() $\Lambda ^{s-1}\subset X$
. The s-planes in
$\Lambda ^{s-1}\subset X$
. The s-planes in
![]() $\mathbb {P}^{N}$
containing
$\mathbb {P}^{N}$
containing
![]() $\Lambda ^{s-1}$
are parametrized by
$\Lambda ^{s-1}$
are parametrized by
![]() $\mathbb {P}^{N-s}$
.
$\mathbb {P}^{N-s}$
.
Arguing as in the proof of Lemma 4.2, we see that requiring such an s-plane to be contained in
![]() $Q_i$
yields s linear equations given by the tangent spaces of
$Q_i$
yields s linear equations given by the tangent spaces of
![]() $Q_i$
at s general points of
$Q_i$
at s general points of
![]() $\Lambda ^{s-1}$
plus a quadratic equation induced by
$\Lambda ^{s-1}$
plus a quadratic equation induced by
![]() $Q_i$
itself.
$Q_i$
itself.
Hence, the points of
![]() $\mathbb {P}^{N-s}$
corresponding to s-planes contained in X are parametrized by a subvariety cut out by
$\mathbb {P}^{N-s}$
corresponding to s-planes contained in X are parametrized by a subvariety cut out by
![]() $sc$
linear equations and c quadratic equations that is an intersection Y of c quadrics in
$sc$
linear equations and c quadratic equations that is an intersection Y of c quadrics in
![]() $\mathbb {P}^{N-s-sc}$
. Since
$\mathbb {P}^{N-s-sc}$
. Since
![]() $\dim (Y) = N-s(c+1)-c> 2^rc-1-c \geq -1$
and
$\dim (Y) = N-s(c+1)-c> 2^rc-1-c \geq -1$
and
![]() $N-s(c+1)+1> 2^rc$
, Remark 2.10 yields that Y has a point and so there is an s-plane through
$N-s(c+1)+1> 2^rc$
, Remark 2.10 yields that Y has a point and so there is an s-plane through
![]() $\Lambda ^{s-1}$
contained in X.
$\Lambda ^{s-1}$
contained in X.
Corollary 4.5. Let
![]() $X = Q_1\cap \dots \cap Q_c\subset \mathbb {P}^{N}$
be a smooth complete intersection of quadrics over a
$X = Q_1\cap \dots \cap Q_c\subset \mathbb {P}^{N}$
be a smooth complete intersection of quadrics over a
![]() $C_r$
field. If
$C_r$
field. If
then X is rational.
Proof. By Proposition 4.4 with
![]() $s = c-1$
, the complete intersection X contains a
$s = c-1$
, the complete intersection X contains a
![]() $(c-1)$
-plane, and hence, the claim follows from Lemma 4.3.
$(c-1)$
-plane, and hence, the claim follows from Lemma 4.3.
We are now ready to prove our first result on unirationality of quintic hypersurfaces.
Proposition 4.6. Let
![]() $X^{n}_5 = \{\overline {f} = 0\}\subset \mathbb {P}^{n+1}$
be a quintic hypersurface of the form
$X^{n}_5 = \{\overline {f} = 0\}\subset \mathbb {P}^{n+1}$
be a quintic hypersurface of the form
with
![]() $A_{i_0,\dots ,i_{n-h}}$
quadratic polynomials. If either
$A_{i_0,\dots ,i_{n-h}}$
quadratic polynomials. If either
-
(i)
 $h\geq 4$
and the complete intersection
$h\geq 4$
and the complete intersection  $$ \begin{align*}W' = \{A_{3,\dots,0} = A_{2,1,0,\dots,0} = x_0 = \dots = x_{n-h} = 0\}\subset\mathbb{P}^{h}_{(y_0,\dots,y_h)} \end{align*} $$
$$ \begin{align*}W' = \{A_{3,\dots,0} = A_{2,1,0,\dots,0} = x_0 = \dots = x_{n-h} = 0\}\subset\mathbb{P}^{h}_{(y_0,\dots,y_h)} \end{align*} $$
contains a line, or
-
(ii)
 $h\geq 5$
and the quadric
$h\geq 5$
and the quadric  $$ \begin{align*}\widetilde{Q} = \{x_0 = \dots = x_{n-h} = A_{3,\dots,0} = 0\}\subset\mathbb{P}^{h}_{(y_0,\dots,y_h)} \end{align*} $$
$$ \begin{align*}\widetilde{Q} = \{x_0 = \dots = x_{n-h} = A_{3,\dots,0} = 0\}\subset\mathbb{P}^{h}_{(y_0,\dots,y_h)} \end{align*} $$
contains a
 $2$
-plane,
$2$
-plane,
and
![]() $X^{n}_5$
is otherwise general, then
$X^{n}_5$
is otherwise general, then
![]() $X_5^{n}$
is unirational.
$X_5^{n}$
is unirational.
Proof. Note that
![]() $X^{n}_5$
is a hypersurface of the form (2.12) in Proposition 2.11. Hence,
$X^{n}_5$
is a hypersurface of the form (2.12) in Proposition 2.11. Hence,
![]() $X^{n}_5$
has multiplicity three along
$X^{n}_5$
has multiplicity three along
![]() $\Lambda = \{x_0 = \dots = x_{n-h} = 0\}$
, and multiplicity two along
$\Lambda = \{x_0 = \dots = x_{n-h} = 0\}$
, and multiplicity two along
![]() $\Lambda ' = \{y_0 = \dots = y_h = x_{n-h} = 0\}$
.
$\Lambda ' = \{y_0 = \dots = y_h = x_{n-h} = 0\}$
.
First, consider
![]() $\text {(i)}$
. Fix a point
$\text {(i)}$
. Fix a point
![]() $p \in \Lambda '$
, say
$p \in \Lambda '$
, say
![]() $p = [1:0:\dots : 0]$
. The lines through p intersecting
$p = [1:0:\dots : 0]$
. The lines through p intersecting
![]() $X_5^n$
at p with multiplicity at least four are parametrized by the variety
$X_5^n$
at p with multiplicity at least four are parametrized by the variety
Assume Y to be unirational. Associating to a general point
![]() $y\in Y$
, representing a line
$y\in Y$
, representing a line
![]() $l_y$
, the fifth intersection point of
$l_y$
, the fifth intersection point of
![]() $l_y$
and
$l_y$
and
![]() $X_5^n$
we get a rational map
$X_5^n$
we get a rational map
Set
![]() $Y_{\psi } = \overline {\psi (Y)}\subset X_5^n$
, and let
$Y_{\psi } = \overline {\psi (Y)}\subset X_5^n$
, and let
be the restriction to
![]() $X_5^n$
of the projection from
$X_5^n$
of the projection from
![]() $\Lambda $
. We want to prove that
$\Lambda $
. We want to prove that
is dominant. Indeed, if so
![]() $Y_{\psi }$
would be a unirational variety transverse to the quadric fibration induced by the projection from
$Y_{\psi }$
would be a unirational variety transverse to the quadric fibration induced by the projection from
![]() $\Lambda $
and dominating
$\Lambda $
and dominating
![]() $\mathbb {P}^{n-h}$
, and Proposition 2.7 would imply that
$\mathbb {P}^{n-h}$
, and Proposition 2.7 would imply that
![]() $X_5^n$
is unirational.
$X_5^n$
is unirational.
Since
![]() $Y_{\psi }$
is unirational it is enough to prove that the induced map
$Y_{\psi }$
is unirational it is enough to prove that the induced map
![]() between the algebraic closures is dominant. Consider the complete intersection
between the algebraic closures is dominant. Consider the complete intersection
A general point of
![]() $z\in Z\subset X^n_5$
represents a line
$z\in Z\subset X^n_5$
represents a line
![]() $l_z$
intersecting
$l_z$
intersecting
![]() $X^n_5$
with multiplicity four at p and multiplicity one at z. Hence,
$X^n_5$
with multiplicity four at p and multiplicity one at z. Hence,
![]() $Z\subset Y_{\psi }$
.
$Z\subset Y_{\psi }$
.
Fix a general point
![]() $q\in \mathbb {P}^{n-h}$
, and consider
$q\in \mathbb {P}^{n-h}$
, and consider
Note that since
![]() $q\in \mathbb {P}^{n-h}$
is defined by
$q\in \mathbb {P}^{n-h}$
is defined by
![]() $n-h$
equations,
$n-h$
equations,
![]() $Z\subset \mathbb {P}^{n+1}_{(x_0,\dots ,x_{n-h},y_0,\dots ,y_h)}$
is cut out by three equations and by hypothesis
$Z\subset \mathbb {P}^{n+1}_{(x_0,\dots ,x_{n-h},y_0,\dots ,y_h)}$
is cut out by three equations and by hypothesis
![]() $n+1-(n-h)-3 = h-2> 0$
. So
$n+1-(n-h)-3 = h-2> 0$
. So
![]() $Z_q$
is nonempty. Then
$Z_q$
is nonempty. Then
![]() $\overline {\pi }_{|W_{\psi }}$
is dominant when restricted to
$\overline {\pi }_{|W_{\psi }}$
is dominant when restricted to
![]() $\overline {Z}$
, and hence, it is dominant.
$\overline {Z}$
, and hence, it is dominant.
Now, we prove that Y is unirational. In
![]() $\mathbb {P}^{n}_{(x_1,\dots ,x_{n-h},y_0,\dots ,y_h)}$
, fix the point
$\mathbb {P}^{n}_{(x_1,\dots ,x_{n-h},y_0,\dots ,y_h)}$
, fix the point
![]() $p' = [1:0:\dots :0]$
. The quadric
$p' = [1:0:\dots :0]$
. The quadric
parametrizes lines that are contained in
Indeed, the tangent cone of
![]() $Y_3$
at
$Y_3$
at
![]() $p'$
is defined by
$p'$
is defined by
![]() $\{A_{2,1,0,\dots ,0} = 0\}$
and
$\{A_{2,1,0,\dots ,0} = 0\}$
and
![]() $\{x_1 = \dots = x_{n-h}= 0\}\subset Y_3$
. So these lines intersect
$\{x_1 = \dots = x_{n-h}= 0\}\subset Y_3$
. So these lines intersect
![]() $Y_3$
with multiplicity three at
$Y_3$
with multiplicity three at
![]() $p'$
and at another point in the linear space
$p'$
and at another point in the linear space
![]() $\{x_1 = \dots = x_{n-h}= 0\}$
.
$\{x_1 = \dots = x_{n-h}= 0\}$
.
Set
![]() $Y_2 = \{A_{3,\dots ,0} = 0\}$
, and let W be the cone over
$Y_2 = \{A_{3,\dots ,0} = 0\}$
, and let W be the cone over
![]() $W'$
with vertex
$W'$
with vertex
![]() $p'$
. Since
$p'$
. Since
![]() $p'$
is in the vertex of
$p'$
is in the vertex of
![]() $Y_2$
, we have that
$Y_2$
, we have that
Furthermore, since
![]() $W'$
contains a line by Lemma 4.3 it is rational, and hence, W is rational as well.
$W'$
contains a line by Lemma 4.3 it is rational, and hence, W is rational as well.
As in the proof of Proposition 3.4, we construct a quadric bundle
![]() $\widetilde {\mathcal {Q}}\rightarrow W$
with
$\widetilde {\mathcal {Q}}\rightarrow W$
with
![]() $(n-4)$
-dimensional fibers whose general point
$(n-4)$
-dimensional fibers whose general point
![]() $(w,l_w)$
represents a point
$(w,l_w)$
represents a point
![]() $w\in W$
and a line
$w\in W$
and a line
![]() $l_w$
which is contained in
$l_w$
which is contained in
![]() $Y_2$
and intersects
$Y_2$
and intersects
![]() $Y_3$
with multiplicity two at w.
$Y_3$
with multiplicity two at w.
Associating to
![]() $(w,l_w)$
the third point of intersection of
$(w,l_w)$
the third point of intersection of
![]() $l_w$
and
$l_w$
and
![]() $Y_3$
, we get a rational map
$Y_3$
, we get a rational map
![]() and arguing as in the proof of Proposition 3.4 we see that such rational map is dominant.
and arguing as in the proof of Proposition 3.4 we see that such rational map is dominant.
Now, we consider
![]() $\text {(ii)}$
. Note that
$\text {(ii)}$
. Note that
is an h-dimensional quadric cone over
![]() $\widetilde {Q}$
with vertex
$\widetilde {Q}$
with vertex
![]() $[1:0:\dots :0]$
. Since
$[1:0:\dots :0]$
. Since
![]() $\widetilde {Q}$
contains a
$\widetilde {Q}$
contains a
![]() $2$
-plane
$2$
-plane
![]() $\widetilde {Q}'$
contains a
$\widetilde {Q}'$
contains a
![]() $3$
-plane
$3$
-plane
![]() $H\subset X^n_5$
. If
$H\subset X^n_5$
. If
![]() $x\in H$
is a general point the lines through x intersecting
$x\in H$
is a general point the lines through x intersecting
![]() $X^n_5$
with multiplicity four at x are parametrized by a complete intersection of a quadric and a cubic in
$X^n_5$
with multiplicity four at x are parametrized by a complete intersection of a quadric and a cubic in
![]() $\mathbb {P}^{n-1}$
. Hence, we get a fibration
$\mathbb {P}^{n-1}$
. Hence, we get a fibration
![]() $\mathcal {Y}_{2,3}\rightarrow H$
whose fiber over a general
$\mathcal {Y}_{2,3}\rightarrow H$
whose fiber over a general
![]() $x\in H$
is a complete intersection
$x\in H$
is a complete intersection
![]() $Y_{2,3,x}$
of a quadric
$Y_{2,3,x}$
of a quadric
![]() $Y_{2,x}\subset \mathbb {P}^{n-1}$
and a cubic
$Y_{2,x}\subset \mathbb {P}^{n-1}$
and a cubic
![]() $Y_{3,x}\subset \mathbb {P}^{n-1}$
. Note that since
$Y_{3,x}\subset \mathbb {P}^{n-1}$
. Note that since
![]() $X_5^n$
is general among the quintics satisfying
$X_5^n$
is general among the quintics satisfying
![]() $(ii)$
for
$(ii)$
for
![]() $x\in H$
both
$x\in H$
both
![]() $Y_{2,x}$
and
$Y_{2,x}$
and
![]() $Y_{2,3,x}$
are smooth.
$Y_{2,3,x}$
are smooth.
The generic fiber of
![]() $\mathcal {Y}_{2,3}\rightarrow H$
is then a complete intersection
$\mathcal {Y}_{2,3}\rightarrow H$
is then a complete intersection
![]() $\mathcal {Y}_{2,3,k(H)} = \mathcal {Y}_{2,k(H)}\cap \mathcal {Y}_{3,k(H)}$
satisfying the hypotheses of Lemma 3.1. Indeed, by considering the
$\mathcal {Y}_{2,3,k(H)} = \mathcal {Y}_{2,k(H)}\cap \mathcal {Y}_{3,k(H)}$
satisfying the hypotheses of Lemma 3.1. Indeed, by considering the
![]() $2$
-plane parametrizing lines in H through a general
$2$
-plane parametrizing lines in H through a general
![]() $x\in H$
we get a
$x\in H$
we get a
![]() $2$
-plane over
$2$
-plane over
![]() $k(H)$
contained in
$k(H)$
contained in
![]() $\mathcal {Y}_{2,k(H)}$
.
$\mathcal {Y}_{2,k(H)}$
.
Therefore, by Lemma 3.1
![]() $\mathcal {Y}_{2,3,k(H)}$
is unirational over
$\mathcal {Y}_{2,3,k(H)}$
is unirational over
![]() $k(H)$
. As usual after replacing H by an open subset, we may assume that
$k(H)$
. As usual after replacing H by an open subset, we may assume that
![]() $\mathcal {Y}_{2,3}$
is irreducible and so we get that
$\mathcal {Y}_{2,3}$
is irreducible and so we get that
![]() $\mathcal {Y}_{2,3}$
is unirational. Now, a general point of
$\mathcal {Y}_{2,3}$
is unirational. Now, a general point of
![]() $\mathcal {Y}_{2,3}$
represents a pair
$\mathcal {Y}_{2,3}$
represents a pair
![]() $(x,l_x)$
with
$(x,l_x)$
with
![]() $x\in H$
general and
$x\in H$
general and
![]() $l_x$
a line intersecting
$l_x$
a line intersecting
![]() $X_5^n$
with multiplicity four at x. As usual, associating to
$X_5^n$
with multiplicity four at x. As usual, associating to
![]() $(x,l_x)\in \mathcal {Y}_{2,3}$
the fifth point of intersection of
$(x,l_x)\in \mathcal {Y}_{2,3}$
the fifth point of intersection of
![]() $l_x$
with
$l_x$
with
![]() $X_5^n$
we get a rational map
$X_5^n$
we get a rational map
Note that
![]() $\dim (\mathcal {Y}_{2,3}) = 3+(n-3) = n$
. Arguing as in the last part of the proof of Proposition 3.4, we see that
$\dim (\mathcal {Y}_{2,3}) = 3+(n-3) = n$
. Arguing as in the last part of the proof of Proposition 3.4, we see that
![]() $\phi $
is generically finite and therefore it is dominant.
$\phi $
is generically finite and therefore it is dominant.
Theorem 4.7. Let
![]() $D\subset \mathbb {P}^{n-h}\times \mathbb {P}^{h+1}$
, with
$D\subset \mathbb {P}^{n-h}\times \mathbb {P}^{h+1}$
, with
![]() $n-h\geq 2$
, be a general divisor of bidegree
$n-h\geq 2$
, be a general divisor of bidegree
![]() $(3,2)$
over a
$(3,2)$
over a
![]() $C_r$
field. If either
$C_r$
field. If either
-
(i)
 $n\geq 4$
,
$n\geq 4$
,
 $2h\geq n+3$
and
$2h\geq n+3$
and
 $h> 2^{r+1}+2$
, or
$h> 2^{r+1}+2$
, or -
(ii)
 $n\geq 6$
,
$n\geq 6$
,
 $h\geq 5$
and
$h\geq 5$
and
 $h> 2^{r}+3$
, or
$h> 2^{r}+3$
, or -
(iii)
 $n-h-1> 3^{r+1}-2$
,
$n-h-1> 3^{r+1}-2$
,
then D is unirational.
Proof. By Proposition 2.11, D is birational to a quintic hypersurface
![]() $X^n_{5}\subset \mathbb {P}^{n+1}$
of the form considered in Proposition 4.6.
$X^n_{5}\subset \mathbb {P}^{n+1}$
of the form considered in Proposition 4.6.
Consider
![]() $\text {(i)}$
. Since,
$\text {(i)}$
. Since,
![]() $h> 2^{r+1}+2$
by Proposition 4.4 the complete intersection
$h> 2^{r+1}+2$
by Proposition 4.4 the complete intersection
![]() $W'$
in Proposition 4.6 contains a line, and hence, Proposition 4.6 yields that
$W'$
in Proposition 4.6 contains a line, and hence, Proposition 4.6 yields that
![]() $X^n_{5}$
is unirational.
$X^n_{5}$
is unirational.
For
![]() $\text {(ii)}$
, note that since
$\text {(ii)}$
, note that since
![]() $h> 2^{r}+3$
Lemma 4.2 implies that the quadric
$h> 2^{r}+3$
Lemma 4.2 implies that the quadric
![]() $\widetilde {Q}$
in Proposition 4.6 contains a
$\widetilde {Q}$
in Proposition 4.6 contains a
![]() $2$
-plane.
$2$
-plane.
Now, consider
![]() $\text {(iii)}$
. The projection
$\text {(iii)}$
. The projection
![]() $\pi _2:D\rightarrow \mathbb {P}^{h+1}$
endows D with a structure of fibration in
$\pi _2:D\rightarrow \mathbb {P}^{h+1}$
endows D with a structure of fibration in
![]() $(n-h-1)$
-dimensional cubic hypersurfaces. Take a general line
$(n-h-1)$
-dimensional cubic hypersurfaces. Take a general line
![]() $L\subset \mathbb {P}^{h+1}$
, and set
$L\subset \mathbb {P}^{h+1}$
, and set
![]() $\mathcal {C}_L = \pi _2^{-1}(L)$
. Then
$\mathcal {C}_L = \pi _2^{-1}(L)$
. Then
![]() $\mathcal {C}_L$
is a fibration in
$\mathcal {C}_L$
is a fibration in
![]() $(n-h-1)$
-dimensional cubic hypersurfaces over
$(n-h-1)$
-dimensional cubic hypersurfaces over
![]() $\mathbb {P}^1$
and since
$\mathbb {P}^1$
and since
![]() $n-h-1> 3^{r+1}-2$
Lemma 4.1 yields that
$n-h-1> 3^{r+1}-2$
Lemma 4.1 yields that
![]() $\mathcal {C}_L$
is unirational. Finally, to conclude it is enough to note that
$\mathcal {C}_L$
is unirational. Finally, to conclude it is enough to note that
![]() $\pi _{|\mathcal {C}_L}:\mathcal {C}_L\rightarrow \mathbb {P}^{n-h}$
is dominant and to apply Proposition 2.7.
$\pi _{|\mathcal {C}_L}:\mathcal {C}_L\rightarrow \mathbb {P}^{n-h}$
is dominant and to apply Proposition 2.7.
Remark 4.8. Take for instance
![]() $r = 0$
that is k is algebraically closed. Remark 2.10 gives the rationality of a
$r = 0$
that is k is algebraically closed. Remark 2.10 gives the rationality of a
![]() $D\subset \mathbb {P}^{n-h}\times \mathbb {P}^{h+1}$
as in Theorem 4.7 for
$D\subset \mathbb {P}^{n-h}\times \mathbb {P}^{h+1}$
as in Theorem 4.7 for
![]() $h> 2^{n-h}-2$
while Theorem 4.7 gives the unirationality of D for
$h> 2^{n-h}-2$
while Theorem 4.7 gives the unirationality of D for
![]() $h> 4$
as long as
$h> 4$
as long as
![]() $n\geq 4$
and
$n\geq 4$
and
![]() $h \geq n-h+3$
. For example, take
$h \geq n-h+3$
. For example, take
![]() $h = 10$
. Then Remark 2.10 yields that D is rational for
$h = 10$
. Then Remark 2.10 yields that D is rational for
![]() $n\leq 13$
while Theorem 4.7 gives the unirationality of D for
$n\leq 13$
while Theorem 4.7 gives the unirationality of D for
![]() $n\leq 17$
.
$n\leq 17$
.
Furthermore, there are cases covered by
![]() $\text {(iii)}$
but not by
$\text {(iii)}$
but not by
![]() $\text {(i)}$
. For instance, by
$\text {(i)}$
. For instance, by
![]() $\text {(iii)}$
we get that a general
$\text {(iii)}$
we get that a general
![]() $D\subset \mathbb {P}^{n-1}\times \mathbb {P}^{2}$
of bidegree
$D\subset \mathbb {P}^{n-1}\times \mathbb {P}^{2}$
of bidegree
![]() $(3,2)$
and dimension at least four is unirational.
$(3,2)$
and dimension at least four is unirational.
For
![]() $r\geq 1$
,
$r\geq 1$
,
![]() $\text {(i)}$
generally performs better that
$\text {(i)}$
generally performs better that
![]() $\text {(ii)}$
. For instance, the case
$\text {(ii)}$
. For instance, the case
![]() $h = 7, n = 11$
is covered by
$h = 7, n = 11$
is covered by
![]() $\text {(i)}$
but not by
$\text {(i)}$
but not by
![]() $\text {(ii)}$
.
$\text {(ii)}$
.
Remark 4.9. In particular, Theorem 4.7 (ii) together with [Reference Auel, Böhning and PirutkaABP18, Theorem A] yields that a very general, meaning outside of a countable union of closed subsets of the corresponding parameter space, divisor of bidegree
![]() $(3,2)$
in
$(3,2)$
in
![]() $\mathbb {P}^3\times \mathbb {P}^2$
, over an algebraically closed field of characteristic zero, is unirational but not stably rational.
$\mathbb {P}^3\times \mathbb {P}^2$
, over an algebraically closed field of characteristic zero, is unirational but not stably rational.
We end this section with our main results on the unirationality of quintic hypersurfaces which are singular along a linear subspace.
Theorem 4.10. Let
![]() $X_5\subset \mathbb {P}^{n+1}$
be a quintic hypersurface over a
$X_5\subset \mathbb {P}^{n+1}$
be a quintic hypersurface over a
![]() $C_r$
field having multiplicity three along an h-plane and otherwise general. Assume that
$C_r$
field having multiplicity three along an h-plane and otherwise general. Assume that
![]() $n-h \geq 2$
. If either
$n-h \geq 2$
. If either
-
(i)
 $n\geq 5$
,
$n\geq 5$
,
 $2h\geq n+4$
and
$2h\geq n+4$
and
 $h> 2^{r+1}+3$
, or
$h> 2^{r+1}+3$
, or -
(ii)
 $n\geq 7$
,
$n\geq 7$
,
 $h\geq 6$
and
$h\geq 6$
and
 $h> 2^{r}+4$
, or
$h> 2^{r}+4$
, or -
(iii)
 $n-h-1> 3^{r+1}-2$
,
$n-h-1> 3^{r+1}-2$
,
then
![]() $X_5$
is unirational.
$X_5$
is unirational.
Similarly, if
![]() $X_5\subset \mathbb {P}^{n+1}$
has multiplicity two along an h-plane with
$X_5\subset \mathbb {P}^{n+1}$
has multiplicity two along an h-plane with
![]() $h\geq 2$
and is otherwise general, and either
$h\geq 2$
and is otherwise general, and either
-
(i)
 $n\geq 5$
,
$n\geq 5$
,
 $2h\leq n-4$
and
$2h\leq n-4$
and
 $n-h> 2^{r+1}+3$
, or
$n-h> 2^{r+1}+3$
, or -
(ii)
 $n\geq 7$
,
$n\geq 7$
,
 $n-h-1\geq 5$
and
$n-h-1\geq 5$
and
 $n-h-1> 2^{r}+3$
, or
$n-h-1> 2^{r}+3$
, or -
(iii)
 $h> 3^{r+1}-1$
,
$h> 3^{r+1}-1$
,
then
![]() $X_5$
is unirational.
$X_5$
is unirational.
Proof. By Lemma 2.4, the exceptional divisor
![]() $\widetilde {E}\subset \widetilde {X}_5$
is a divisor of bidegree
$\widetilde {E}\subset \widetilde {X}_5$
is a divisor of bidegree
![]() $(3,2)$
in
$(3,2)$
in
![]() $\mathbb {P}^{n-h}\times \mathbb {P}^h$
. Since
$\mathbb {P}^{n-h}\times \mathbb {P}^h$
. Since
![]() $X_5$
is general,
$X_5$
is general,
![]() $\widetilde {E}$
maps dominantly onto
$\widetilde {E}$
maps dominantly onto
![]() $\mathbb {P}^{n-h}$
, and hence, to conclude we apply Proposition 2.7 and Theorem 4.7. For the second statement, it is enough to argue as in the previous case on a divisor of bidegree
$\mathbb {P}^{n-h}$
, and hence, to conclude we apply Proposition 2.7 and Theorem 4.7. For the second statement, it is enough to argue as in the previous case on a divisor of bidegree
![]() $(2,3)$
in
$(2,3)$
in
![]() $\mathbb {P}^{n-h}\times \mathbb {P}^h$
.
$\mathbb {P}^{n-h}\times \mathbb {P}^h$
.
Proposition 4.11. Let
![]() $X_5\subset \mathbb {P}^{n+1}$
be a quintic hypersurface over a field k having multiplicity three along an
$X_5\subset \mathbb {P}^{n+1}$
be a quintic hypersurface over a field k having multiplicity three along an
![]() $(n-1)$
-plane and otherwise general. If either
$(n-1)$
-plane and otherwise general. If either
-
(i)
 $n\geq 5$
and k is either a number field or a real closed field, or
$n\geq 5$
and k is either a number field or a real closed field, or -
(ii) k is
 $C_r$
,
$C_r$
,
 $n> 4$
and
$n> 4$
and
 $n> 2^r$
,
$n> 2^r$
,
then
![]() $X_5$
is unirational.
$X_5$
is unirational.
Proof. The exceptional divisor
![]() $\widetilde {E}\subset \widetilde {X}_5$
is a general divisor of bidegree
$\widetilde {E}\subset \widetilde {X}_5$
is a general divisor of bidegree
![]() $(3,2)$
in
$(3,2)$
in
![]() $\mathbb {P}^{1}\times \mathbb {P}^{n-1}$
. By [Reference MassarentiMas22, Corollary 4.13, Lemma 4.18] and Remark 2.10, under our hypotheses
$\mathbb {P}^{1}\times \mathbb {P}^{n-1}$
. By [Reference MassarentiMas22, Corollary 4.13, Lemma 4.18] and Remark 2.10, under our hypotheses
![]() $\widetilde {E}$
has a point and hence [Reference MassarentiMas22, Theorem 1.8] yields that
$\widetilde {E}$
has a point and hence [Reference MassarentiMas22, Theorem 1.8] yields that
![]() $\widetilde {E}$
is unirational. To conclude, it is enough to argue as in the proof of Theorem 4.10 applying Propositions 2.7.
$\widetilde {E}$
is unirational. To conclude, it is enough to argue as in the proof of Theorem 4.10 applying Propositions 2.7.
Remark 4.12. When k is a real closed field, the unirationality of a quintic hypersurface
![]() $X_5\subset \mathbb {P}^{n+1}$
as in Proposition 4.11 follows from [Reference KollárKol99, Corollary 1.8].
$X_5\subset \mathbb {P}^{n+1}$
as in Proposition 4.11 follows from [Reference KollárKol99, Corollary 1.8].
Proposition 4.13. Let
![]() $X_d\subset \mathbb {P}^{n+1}$
be a hypersurface of degree d over a field k having multiplicity
$X_d\subset \mathbb {P}^{n+1}$
be a hypersurface of degree d over a field k having multiplicity
![]() $d-2$
along an h-plane and otherwise general. Assume that
$d-2$
along an h-plane and otherwise general. Assume that
![]() $(h+1)(d-2)$
is odd. If either
$(h+1)(d-2)$
is odd. If either
-
(i)
 $d\leq \frac {5h+3}{h+1}$
, or
$d\leq \frac {5h+3}{h+1}$
, or -
(ii)
 $d\leq \frac {6h+1}{h+1}$
,
$d\leq \frac {6h+1}{h+1}$
,
 $h\leq 4$
, k is
$h\leq 4$
, k is
 $C_r$
and
$C_r$
and
 $h+1> 2^{r+n-h-1}$
,
$h+1> 2^{r+n-h-1}$
,
then
![]() $X_5$
is unirational.
$X_5$
is unirational.
Proof. In this case, the exceptional divisor
![]() $\widetilde {E}\subset \widetilde {X}_d$
is a general divisor of bidegree
$\widetilde {E}\subset \widetilde {X}_d$
is a general divisor of bidegree
![]() $(d-2,2)$
in
$(d-2,2)$
in
![]() $\mathbb {P}^{n-h}\times \mathbb {P}^{h}$
. Note that the discriminant of the quadric bundle
$\mathbb {P}^{n-h}\times \mathbb {P}^{h}$
. Note that the discriminant of the quadric bundle
![]() $\widetilde {E}\rightarrow \mathbb {P}^{n-h}$
has degree
$\widetilde {E}\rightarrow \mathbb {P}^{n-h}$
has degree
![]() $(h+1)(d-2)$
. Hence, the claim follows from [Reference MassarentiMas22, Theorem 1.7] and Propositions 2.7.
$(h+1)(d-2)$
. Hence, the claim follows from [Reference MassarentiMas22, Theorem 1.7] and Propositions 2.7.
Acknowledgements
I would like to thank the referee for the careful reading that helped me to improve the paper.
Competing interest
The authors have no competing interest to declare.