Hostname: page-component-5c6d5d7d68-lvtdw Total loading time: 0 Render date: 2024-08-06T22:25:30.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Character sums and small eigenvalues for Г0(p)

Published online by Cambridge University Press:  18 May 2009

Henryk Iwaniec
Henryk Iwaniec
Affiliation:
Polish Academy of Sciences, Mathematics Institute, Ul. Sniadeckich 8, (00-950) Warsaw, Poland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Δ denote the Laplace operator acting on the space L2(Г/H) of automorphic functions with respect to a congruence group Г, square integrable over the fundamental domain F=Г/H. It is known that Δ has a point spectrum

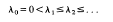
with (Weyl's law)

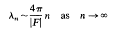
and it has a purely continuous spectrum on [¼,∞) of finite multiplicity equal to the number of inequivalent cusps. The eigenpacket of the continuous spectrum is formed by the Eisenstein series Ea(z, s) on s = ½+it where a ranges over inequivalent cusps. The eigenfunctions ui(z) with positive eigenvalues are Maass cusp forms.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 27 , October 1985 , pp. 99 - 116
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Deshouillers, J.-M. and Iwaniec, H., Kloosterman sums and Fourier coefficients of cusp forms, Invent. Math. 70 (1982), 219–288.CrossRefGoogle Scholar
2.Gelbart, S. S. and Jacquet, H., A relation between automorphic representations of GL(2) and GL(3), Ann. Ecole Norm. Sup. 11 (1978), 471–542.CrossRefGoogle Scholar
3.Huxley, M. N., Introduction to Kloostermania, in Banach Center Publ., 17 (PWN, Warsaw, 1984).Google Scholar
4.Huxley, M. N., preprint (1983).Google Scholar
5.Iwaniec, H., Prime geodesic theorem, J. Reine Angew. Math., 349 (1984), 136–159.Google Scholar
6.Iwaniec, H. and Szmidt, J., Density theorems for exceptional eigenvalues of Laplacian for congruence groups, Banach Center Publ., 17 (PWN, Warsaw, 1984).Google Scholar
7.Linnik, Yu. V., Additive problems and eigenvalues of the modular operators, Proceedings of the International Congress of Mathematicians (Inst. Mittag-Leffler, Djursholm 1963), 270–284.Google Scholar
8.Schmidt, W. M., Lectures on equations over finite fields, an elementary approach, Lecture Notes in Mathematics 536 (Springer, 1976).CrossRefGoogle Scholar
9.Selberg, A., On the estimation of Fourier coefficients of modular forms, Proc. Sympos. Pure Math. 8 (1965), 1–15.CrossRefGoogle Scholar