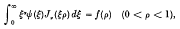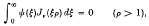Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Copson, E. T.
1961.
On Certain Dual Integral Equations.
Proceedings of the Glasgow Mathematical Association,
Vol. 5,
Issue. 1,
p.
21.
Lowengrub, M.
and
Sneddon, I. N.
1962.
An Axisymmetric Boundary Value Problem of Mixed Type for a Half-space.
Proceedings of the Edinburgh Mathematical Society,
Vol. 13,
Issue. 1,
p.
39.
Erdélyi, A.
and
Sneddon, I. N.
1962.
Fractional Integration and Dual Integral Equations.
Canadian Journal of Mathematics,
Vol. 14,
Issue. ,
p.
685.
Burlak, J.
1962.
A Pair of Dual Integral Equations Occurring in Diffraction Theory.
Proceedings of the Edinburgh Mathematical Society,
Vol. 13,
Issue. 2,
p.
179.
Lowengrub, M.
and
Sneddon, I. N.
1963.
The solution of a pair of dual integral equations.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 1,
p.
14.
Williams, W. E.
1964.
The solution of dual series and dual integral equations.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 3,
p.
123.
Srivastav, R. P.
1964.
A Pair of Dual Integral Equations Involving Bessel Functions of the First and the Second Kind.
Proceedings of the Edinburgh Mathematical Society,
Vol. 14,
Issue. 2,
p.
149.
Sneddon, Ian N.
1965.
A note on the problem of the penny-shaped crack.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 61,
Issue. 2,
p.
609.
Sneddon, Ian N.
1966.
The Reissner-Sagoci problem .
Proceedings of the Glasgow Mathematical Association,
Vol. 7,
Issue. 3,
p.
136.
Lowengrub, M.
1966.
A Note on Griffith Cracks.
Proceedings of the Edinburgh Mathematical Society,
Vol. 15,
Issue. 2,
p.
131.
Keer, L. M.
1967.
Mixed boundary-value problems for an elastic half-space.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 4,
p.
1379.
Kesarwani, Roop Narain
1967.
Fractional integration and certain dual integral equations.
Mathematische Zeitschrift,
Vol. 98,
Issue. 1,
p.
83.
Sneddon, Ian N.
1969.
Transform Solutions of Crack Problems in the Theory of Elasticity.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 49,
Issue. 1-2,
p.
15.
Tweed, John
1969.
A note on the thermoelastic problem for a penny-shaped crack.
Glasgow Mathematical Journal,
Vol. 10,
Issue. 2,
p.
169.
Sneddon, I. N.
and
Tweed, J.
1971.
VI.—The Stress Intensity Factors for a Griffith Crack in an Elastic Body in which there is an Asymmetrical Distributtion of Body Forces.
Proceedings of the Royal Society of Edinburgh. Section A. Mathematical and Physical Sciences,
Vol. 69,
Issue. 2,
p.
85.
Tweed, J.
1973.
The solution of some dual equations with an application in the theory of elasticity.
Journal of Engineering Mathematics,
Vol. 7,
Issue. 3,
p.
273.
Chakrabarti, A.
1974.
Certain Dual Series Relations Involving Bessel Functions Arising in Crack Problems.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 54,
Issue. 6,
p.
436.
Dhawan, G. K.
1975.
Effect of rigid inclusions in Griffith cracks in an infinite transversely isotropic medium.
Acta Mechanica,
Vol. 21,
Issue. 1-2,
p.
115.
Sneddon, Ian Naismith
1975.
Fractional Calculus and Its Applications.
Vol. 457,
Issue. ,
p.
37.
Goodman, L. E.
and
Keer, L. M.
1975.
The mechanics of the contact between deformable bodies.
p.
127.