Article contents
Inductive and projective limits of normed spaces
Published online by Cambridge University Press: 18 May 2009
Extract
Let {Ui, Uij} be an inductive system of normed linear spaces Ui and continuous linear maps uij; Uj → Ui. (We write j ≺ i if uij: Uj → Ui.) An inductive limit of the system with respect to a class 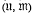 of spaces A in
of spaces A in 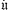 and maps f in
and maps f in 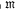 is a space Uu in Uu and a system ui → Uu of maps in
is a space Uu in Uu and a system ui → Uu of maps in 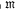 such that (i)
such that (i) 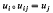 whenever j ≺ i, and that (ii) if A is any space in
whenever j ≺ i, and that (ii) if A is any space in 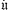 and fi: Ui → A is any system of maps in
and fi: Ui → A is any system of maps in 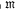 for which
for which 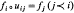 then there is a unique map f: Uu → A in
then there is a unique map f: Uu → A in 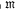 such that fi = fo ui for each i. If
such that fi = fo ui for each i. If 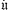 is the class of all vector spaces and
is the class of all vector spaces and 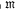 is the class of linear maps, we obtain the algebraic inductive limit, which we denote simply by U. The usual choice is to take
is the class of linear maps, we obtain the algebraic inductive limit, which we denote simply by U. The usual choice is to take 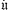 to be the class of locally convex spaces and
to be the class of locally convex spaces and 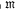 the class of continuous linear maps; the inductive limit UL then always exists [1, § 16 C]. If
the class of continuous linear maps; the inductive limit UL then always exists [1, § 16 C]. If 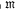 is again the continuous linear mappings but
is again the continuous linear mappings but 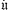 contains only normed spaces, the corresponding inductive limit UN may not always exist. However, if in addition we require that
contains only normed spaces, the corresponding inductive limit UN may not always exist. However, if in addition we require that 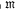 contains just contractions (norm-decreasing linear mappings), then an inductive limit Uc will exist if every uij is a contraction [2]. We shall give a condition under which these limits coincide (as far as possible), and consider the corresponding condition for projective limits.
contains just contractions (norm-decreasing linear mappings), then an inductive limit Uc will exist if every uij is a contraction [2]. We shall give a condition under which these limits coincide (as far as possible), and consider the corresponding condition for projective limits.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1968
References
REFERENCES
- 1
- Cited by




