Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-08T08:49:27.248Z Has data issue: false hasContentIssue false
  • English
  • Français

Khinchin's inequality for operators

Published online by Cambridge University Press:  18 May 2009

G. J. O. Jameson
G. J. O. Jameson
Affiliation:
Department of Mathematics and Statistics, Lancaster University, Lancaster LA1 4YF, England, email: g.jameson@lancaster.ac.uk
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 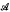be either a C*-algebra (with norm ∥ ∥) or a symmetric ideal of operators on a Hilbert space (with norm denoted by σ). Let a1…, an be self-adjoint elements, and let a0 = .

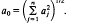Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 3 , September 1996 , pp. 327 - 336
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Garling, D. J. H. and Tomczak-Jaegermann, N., The cotype and uniform convexity of unitary ideals, Israel J. Math. 45 (1983), 175–197.CrossRefGoogle Scholar
2.Gokhberg, I. C. and Krein, M. G., Introduction to the theory of linear nonselfadjoint operators (Amer. Math. Soc., 1969).Google Scholar
3.Haagerup, U., The Grothendieck inequality for bilinear forms on C*-algebras, Advances in Math. 56 (1985), 93–116.CrossRefGoogle Scholar
4.Jameson, G. J. O., Summing and nuclear norms in Banach space theory, London Math. Soc. Student Texts 8 (Cambridge University Press, 1987).CrossRefGoogle Scholar
5.Lance, E. C., Hilbert C*-modules, London Math. Soc. Lecture Notes No. 210 (Cambridge University Press, 1995).CrossRefGoogle Scholar
6.Latala, R. and Oleszkiewicz, K., On the best constant in the Khintchine-Kahane inequality, Studia Math. 109 (1994), 101–104.Google Scholar
7.Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces II (Springer-Verlag, 1979).CrossRefGoogle Scholar
8.Lust-Piquard, F., A Grothendieck factorization theorem on 2-convex Schatten spaces, Israel J. Math. 79 (1992), 331–365.CrossRefGoogle Scholar
9.Lust-Piquard, F. and Pisier, G., Non-commutative Khintchine and Paley inequalities, Arkiv für matematik 29 (1991), 241–260.CrossRefGoogle Scholar
10.Pisier, G., Grothendieck's theorem for non-commutative C*-algebras with an appendix on Grothendieck's constants, J. Functional Anal. 29 (1978), 397–415.CrossRefGoogle Scholar
11.Simon, B., Trace ideals and their applications, London Math. Soc, Lecture Notes No. 35 (Cambridge University Press, 1979).Google Scholar