Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-22T08:11:45.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Notes on hyperelliptic mapping class groups

Part of: Arithmetic problems. Diophantine geometry Curves (Co)homology theory

Published online by Cambridge University Press:  31 October 2023

Marco Boggi Open the ORCID record for Marco Boggi [Opens in a new window]
Marco Boggi*
Affiliation:
Instituto de Matemática e Estatística, Universidade Federal Fluminense, Niterói, RJ, 24210-200, Brazil
*
Email: marco.boggi@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Hyperelliptic mapping class groups are defined either as the centralizers of hyperelliptic involutions inside mapping class groups of oriented surfaces of finite type or as the inverse images of these centralizers by the natural epimorphisms between mapping class groups of surfaces with marked points. We study these groups in a systematic way. An application of this theory is a counterexample to the genus 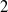$2$ case of a conjecture by Putman and Wieland on virtual linear representations of mapping class groups. In the last section, we study profinite completions of hyperelliptic mapping class groups: we extend the congruence subgroup property to the general class of hyperelliptic mapping class groups introduced above and then determine the centralizers of multitwists and of open subgroups in their profinite completions.

Keywords

Hyperelliptic mapping class groupstopological surfacesmoduli of curvesvirtual linear representations of mapping class groupsprofinite hyperelliptic mapping class groups

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Secondary: 14F45: Topological properties 14G32: Universal profinite groups (relationship to moduli spaces, projective and moduli towers, Galois theory)
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 66 , Issue 1 , January 2024 , pp. 126 - 161
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asada, M., The faithfulness of the monodromy representations associated with certain families of algebraic curves, J. Pure Appl. Algebra 159(2-3) (2001), 123–147.CrossRefGoogle Scholar
Birman, J. S., Braids, links, and mapping class groups, Annals of Mathematics Studies, vol. 82 (Princeton University Press, Princeton, NJ, 1974).Google Scholar
Birman, J. S. and Hilden, H. M., On the mapping class groups of closed surfaces as covering spaces, in Advances in the theory of Riemann surfaces (Proc. Conf., Stony Brook, N.Y., 1969), Annals of Mathematics Studies, vol. 66 (Princeton University Press, Princeton, NJ, 1971), 81–115.CrossRefGoogle Scholar
Birman, J. S. and Hilden, H. M., Lifting and projecting homeomorphisms, Arch. Math. 23(1) (1972), 428–434.CrossRefGoogle Scholar
Boggi, M., Profinite Teichmüller theory, Math. Nach. 279(9-10) (2006), 953–987.CrossRefGoogle Scholar
Boggi, M., The congruence subgroup property for the hyperelliptic Teichmüller modular group: the open surface case, Hiroshima Math. J. 39(3) (2009), 351–362.CrossRefGoogle Scholar
Boggi, M., Fundamental groups of moduli stacks of stable curves of compact type, Geom. Topol. 13 (2009), 247–276.CrossRefGoogle Scholar
Boggi, M., On the procongruence completion of the Teichmüller modular group, Trans. Am. Math. Soc. 366(10) (2014), 5185–5221.CrossRefGoogle Scholar
Boggi, M. and Zalesskii, P., A restricted Magnus property for profinite surface groups, Trans. Am. Math. Soc. 371(1) (2019), 729–753.CrossRefGoogle Scholar
Boggi, M., Galois covers of moduli spaces of curves and loci of curves with symmetries, Geom. Dedic. 168(1) (2014), 113–142.CrossRefGoogle Scholar
Boggi, M., Congruence topologies on the mapping class groups, J. Algebra 546 (2020), 518–552.CrossRefGoogle Scholar
Funar, M. Boggi L., Automorphisms of procongruence curve and pants complexes, J. Topol. 16(3) (2023), 936–989. DOI: 10.1112/topo.12306.Google Scholar
Boggi, M., Linear representations of hyperelliptic mapping class groups, Mich. Math. J. 71(1) (2022), 1–23. DOI: 10.1307/mmj/20195783.CrossRefGoogle Scholar
Brendle, T. and Margalit, D., Point pushing, homology, and the hyperelliptic involution, Mich. Math. J. 62(3) (2013), 451–473.CrossRefGoogle Scholar
Deligne, P., Théorème de Lefschetz et critères de dégénérescence de suites spectrales, Publ. Math. IHÉS 35 (1968), 259–278.CrossRefGoogle Scholar
Farb, B. and Margalit, D., A primer on mapping class group, Princeton Mathematical Series, vol. 49 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Funar, L., On the TQFT representations of the mapping class groups, Pac. J. Math. 188(2) (1999), 251–274.CrossRefGoogle Scholar
Ghigi, A. and Tamborini, C., A topological construction of families of Galois covers of the line, 2023. Available at https://arxiv.org/abs/2204.07817v2 Google Scholar
González-Díez, G. and Harvey, W. J., Moduli of Riemann surfaces with symmetry, in Discrete groups and geometry, LMSLNS (Harvey, W. J. and Maclachlan, C., Editors), vol. 173 (Cambridge University press, Cambridge, 1992), 75–93.CrossRefGoogle Scholar
Grossman, E. K., On residual finiteness of certain mapping class groups, J. Lond. Math. Soc. (2) 9 (1974), 160–164.CrossRefGoogle Scholar
Harer, J., Stability of the homology of the mapping class group of orientable surfaces, Ann. Math. 121(2) (1985), 215–249.CrossRefGoogle Scholar
Harvey, W. J., Boundary structure of the modular group, in Riemann surfaces and related topics: Proceedings of the 1978 Stony Brook Conference (State Univ. New York, Stony Brook, N.Y., 1978), Annals of Mathematics Studies, vol. 97 (Princeton University Press, Princeton, NJ, 1981), 245–251.CrossRefGoogle Scholar
Hoshi, Y. and Ijima, Y., A pro- $\ell$ version of the congruence subgroup problem for mapping class groups of genus 1, J. Algebra 520 (2019), 1–31.CrossRefGoogle Scholar
Humphries, S. P., Normal closures of powers of Dehn twists in mapping class groups, Glasg. Math. J. 34(3) (1992), 313–317.CrossRefGoogle Scholar
Knudsen, F. F., The projectivity of the moduli space of stable curves, II. The stacks $M_{g,n}$ , Math. Scan. 52 (1983), 161–199.CrossRefGoogle Scholar
Maclachlan, C. and Harvey, W. J., On mapping-class groups and Teichmüller spaces, Proc. Lond. Math. Soc. (3) 30 (1975), 496–512.CrossRefGoogle Scholar
Margalit, D. and Winarski, R. R., Braid groups and mapping class groups: The Birman–Hilden theory, Bull. Lond. Math. Soc. 53(3) (2021), 643–659.CrossRefGoogle Scholar
Marković, V., Unramified correspondences and virtual properties of mapping class groups, Bull. Lond. Math. Soc. 54(6) (2022), 2324–2337.CrossRefGoogle Scholar
Masbaum, G., An element of infinite order in TQFT-representations of mapping class groups, in Low-dimensional topology (Funchal, 1998), Contemporary Mathematics, vol. 233 (American Mathematical Society, Providence, RI, 1998), 137–139.Google Scholar
Putman, A. and Wieland, B., Abelian quotients of the mapping class group and higher Prym representations, J. Lond. Math. Soc. (2) 88(1) (2013), 79–96.CrossRefGoogle Scholar
Stylianakis, C., The normal closure of a power of a half-twist has infinite index in the mapping class group of a punctured sphere, J. Topol. Anal. 11(02) (2019), 273–292. DOI: 10.1142/S1793525319500122.CrossRefGoogle Scholar
Serre, J.-P., Cohomologie galoisienne. Cinquième édition, révisée et complétée, Lecture Notes in Mathematics, vol. 5 (Springer, Cham, 1997).Google Scholar