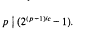Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-03T13:21:15.904Z Has data issue: false hasContentIssue false
  • English
  • Français

On the theorem of Wójcik

Published online by Cambridge University Press:  18 May 2009

A. Rotkiewicz
A. Rotkiewicz
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Ul. Śniadeckich 8, 00-950 Warszawa, Poland Technical University in BiałystokUl. Wiejska 45, 15-351 Bialystok, Poland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the paper [3] the following lemma was proved.

Lemma. Let a, b and c be positive integers such that a and be are relatively prime. Then there are infinitely many primes p in the arithmetic progression ax + b (x = 0,1,2,…) such that

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 2 , May 1996 , pp. 157 - 162
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Durst, L. K., Exceptional real Lehmer sequences, Pacific J. Math. 9 (1959), 437–441.CrossRefGoogle Scholar
2.Lehmer, D. H., An extended theory of Lucas functions, Ann. Math. (2) 31 (1930), 419–448.CrossRefGoogle Scholar
3.Rotkiewicz, A., On the prime factors of the number 2P−1–1, Glasgow Math. J. 9 (1968), 83–86.CrossRefGoogle Scholar
4.Rotkiewicz, A., On the pseudoprimes of the form ax + b with respect to the sequence of Lehmer, Bull. Acad. Polon. Sci. Ser. Sci. Math. Astronom. Phys. 20 (1972), 349–354.Google Scholar
5.Rotkiewicz, A., On Euler Lehmer pseudoprimes and strong Lehmer pseudoprimes with parameters L, Q in arithmetic progressions, Math. Comp. 39 (1982), 239–247.Google Scholar
6.Rotkiewicz, A., On strong Lehmer pseudoprimes in the case of negative discriminant in arithmetic progression, Ada Arith. 68 (1994), 145–151.CrossRefGoogle Scholar
7.Schinzel, A., The intrinsic divisors of Lehmer numbers in the case of negative discriminant, Ark. Math. 4 (1962), 413–416.CrossRefGoogle Scholar
8.Stewart, C. L., Primitive divisors of Lucas and Lehmer numbers, Transcendence Theory: Advances and Application (Academic Press, 1977), 79–92.Google Scholar
9.Ward, M., The intrinsic divisors of Lehmer numbers, Ann. Math..(2) 62 (1955), 230–236.CrossRefGoogle Scholar
10.Wójcik, J., Contribution to the theory of Kummer extension, Ada Arith. 40 (1982), 155–174.CrossRefGoogle Scholar
11.Wójcik, J., On the density of some sets of primes connected with cyclotomic polynomials, Ada Arith. 41 (1982), 117–131.CrossRefGoogle Scholar