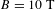1 Introduction
Capacitor coils are a type of laser-driven solenoid that consists of two metal plates held in parallel, connected by a loop of wire or metallic ribbon[Reference Daido, Miki, Mima, Fujita, Sawai, Fujita, Kitagawa, Nakai and Yamanaka1–Reference Zhang, Zhu, Li, Jiang, Yuan, Wei, Liang, Wang, Zhao, Zhong, Han, Hua, Zhu, Zhu, Wang, Fang and Zhang3]. A high-energy laser beam is used to accelerate hot electrons[Reference Gardner, Herbst, Young, Stamper, Obenschain, Manka, Kearney, Grun, Duston and Burkhalter4, Reference Stamper, Papadopoulos, Sudan, Dean, McLean and Dawson5] from the rear plate (anode) onto the front plate (cathode)[Reference Tikhonchuk, Bailly-Grandvaux, Santos and Poyé6]. A return current is then established along the connecting loop, generating a quasi-static magnetic field that can be used in high energy density physics experiments[Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody2, Reference Woolsey, Ali, Evans, Grundy, Pestehe, Carolan, Conway, Dendy, Helander, McClements, Kirk, Norreys, Notley and Rose7, Reference Santos, Bailly-Grandvaux, Ehret, Arefiev, Batani, Beg, Calisti, Ferri, Florido, Forestier-Colleoni, Fujioka, Gigosos, Giuffrida, Gremillet, Honrubia, Kojima, Korneev, Law, Marquès, Morace, Mossé, Peyrusse, Rose, Roth, Sakata, Schaumann, Suzuki-Vidal, Tikhonchuk, Toncian, Woolsey and Zhang8]. There are numerous potential applications of uniform magnetic fields exceeding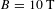 
$B=10~\text{T}$. Several studies suggest that magnetic fields can be used to trap fusion alpha particles and hot electrons, relaxing implosion requirements for ignition[Reference Perkins, Logan, Zimmerman and Werner9–Reference Hohenberger, Chang, Fiksel, Knauer, Betti, Marshall, Meyerhofer, Séguin and Petrasso11]. Strong magnetic fields may also be used to guide charged particle beams[Reference Bailly-Grandvaux, Santos, Bellei, Forestier-Colleoni, Fujioka, Giuffrida, Honrubia, Batani, Bouillaud, Chevrot, Cross, Crowston, Dorard, Dubois, Ehret, Gregori, Hulin, Kojima, Loyez, Marquès, Morace, Nicolaï, Roth, Sakata, Schaumann, Serres, Servel, Tikhonchuk, Woolsey and Zhang12], generate high-power circularly polarized laser pulses[Reference Weng, Zhao, Sheng, Yu, Luan, Chen, Yu, Murakami, Mori and Zhang13], reduce backward stimulated Raman scattering[Reference Winjum, Tsung and Mori14] or amplify laser power by magnetized low-frequency scattering[Reference Edwards, Shi, Mikhailova and Fisch15].
Capacitor coil magnetic fields of 1–1000 T have been reported at different laser facilities using a range of diagnostics, although harsh laser-plasma conditions make it difficult to reliably estimate the magnetic field inside the coil loop[Reference Daido, Miki, Mima, Fujita, Sawai, Fujita, Kitagawa, Nakai and Yamanaka1–Reference Zhang, Zhu, Li, Jiang, Yuan, Wei, Liang, Wang, Zhao, Zhong, Han, Hua, Zhu, Zhu, Wang, Fang and Zhang3, Reference Santos, Bailly-Grandvaux, Ehret, Arefiev, Batani, Beg, Calisti, Ferri, Florido, Forestier-Colleoni, Fujioka, Gigosos, Giuffrida, Gremillet, Honrubia, Kojima, Korneev, Law, Marquès, Morace, Mossé, Peyrusse, Rose, Roth, Sakata, Schaumann, Suzuki-Vidal, Tikhonchuk, Toncian, Woolsey and Zhang8, Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, d’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyé, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey16–Reference Law, Bailly-Grandvaux, Morace, Sakata, Matsuo, Kojima, Lee, Vaisseau, Arikawa, Yogo, Kondo, Zhang, Bellei, Santos, Fujioka and Azechi19]. High-frequency B-dot probes can measure the full time evolution of a capacitor coil magnetic field, but are highly sensitive to electromagnetic pulse noise[Reference Bradford, Woolsey, Scott, Liao, Liu, Zhang, Zhu, Armstrong, Astbury, Brenner, Brummitt, Consoli, East, Gray, Haddock, Huggard, Jones, Montgomery, Musgrave, Oliveira, Rusby, Spindloe, Summers, Zemaityte, Zhang, Li, McKenna and Neely20, Reference Poyé, Hulin, Bailly-Grandvaux, Dubois, Ribolzi, Raffestin, Bardon, Lubrano-Lavaderci, D’Humières, Santos, Nicolaï and Tikhonchuk21] and must be positioned several centimetres from the target to avoid radiation damage. This introduces significant errors in the signal analysis because the magnetic field geometry must be simulated and extrapolated over a long distance. These simulations also require the target current geometry to be known accurately, which is difficult in a complex, closed geometry that combines an expanding plate plasma with photoionization effects[Reference Lichtman and Ready22]. Faraday rotation has been used as a localized magnetic field diagnostic, but the birefringent crystals responsible for polarization of the probe beam must be shielded from plasma X-rays to avoid crystal blanking[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, d’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyé, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey16]. This is challenging in a millimetre-scale loop where shorting of the capacitor must be avoided. In light of these limitations, proton deflectometry is frequently used to corroborate inductive and magneto-optic measurements[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, d’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyé, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey16, Reference Law, Bailly-Grandvaux, Morace, Sakata, Matsuo, Kojima, Lee, Vaisseau, Arikawa, Yogo, Kondo, Zhang, Bellei, Santos, Fujioka and Azechi19].
Proton deflectometry with radiochromic film[Reference Dempsey, Low, Mutic, Markman, Kirov, Nussbaum and Williamson23] (RCF) is an ideal diagnostic of capacitor coil experiments because it can produce multi-dimensional images of electromagnetic fields with micron spatial and picosecond temporal resolution[Reference Kugland, Ryutov, Plechaty, Ross and Park24–Reference Kasim, Ceurvorst, Ratan, Sadler, Chen, Sävert, Trines, Bingham, Burrows, Kaluza and Norreys26]. When a proton beam passes across a capacitor coil target, the proton trajectories are modified by strong electric and magnetic fields; these protons then propagate through space until they strike a stack of RCF, where they deposit their energy in different layers of film according to their Bragg curve[Reference Kugland, Ryutov, Plechaty, Ross and Park24]. The protons in our experiment were generated by the target normal sheath acceleration (TNSA) mechanism[Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely27]. TNSA-generated proton beams have a broad spectral range and probe the target at different times corresponding to the proton time of flight from source to target. Previous capacitor coil experiments have focused on proton deflectometry perpendicular to the loop axis[Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, d’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyé, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey16, Reference Gao, Ji, Fiksel, Fox, Evans and Alfonso17], where protons on one side of the loop are deflected radially outwards and protons on the opposite side are pinched radially inwards by the poloidal magnetic field. These experiments produce a distinctive teardrop-shaped proton void, with a width proportional to the square root of the loop current[Reference Gao, Ji, Fiksel, Fox, Evans and Alfonso17]. It is difficult to extract a definitive measurement of the magnetic field because the void width is also affected by electric fields in the target[Reference Santos, Bailly-Grandvaux, Ehret, Arefiev, Batani, Beg, Calisti, Ferri, Florido, Forestier-Colleoni, Fujioka, Gigosos, Giuffrida, Gremillet, Honrubia, Kojima, Korneev, Law, Marquès, Morace, Mossé, Peyrusse, Rose, Roth, Sakata, Schaumann, Suzuki-Vidal, Tikhonchuk, Toncian, Woolsey and Zhang8, Reference Wang, Cai, Teng, Chen, He, Shan, Lu, Wu, Zhang, Hong, Bi, Zhang, Liu, Xue, Li, Liu, He, Jiao, Dong, Zhang, He, Cui, Xie, Yuan, Tian, Wang, Zhou, Deng, Zhang, Zhou, Cao, Zhang, Zhu, He and Gu28]. Breaking the degeneracy of the electric and magnetic fields is essential when assessing the suitability of capacitor coil targets for magnetized high energy density experiments. To reliably quantify the magnetic field strength in a capacitor coil target, we require monoenergetic proton images of the loop at different energies or proton probing from multiple directions.
In this paper, we present proton probing of a capacitor coil target along two axes. Figure 1 shows RCF data parallel and perpendicular to the axis of a capacitor coil loop. In the perpendicular orientation, an inverted teardrop is formed as protons are deflected radially away from the top of the loop (wire current directed out of the page, magnetic field anticlockwise) and pinched radially inwards towards the bottom of the loop (wire current directed into the page, magnetic field clockwise). The proton beam was centred lower on the target in the parallel orientation, so the wire loop and capacitor coil plates are clearly visible. A metal grid (Au) has been interposed between the proton source and capacitor coil, leaving a mesh imprint in the beam that is warped by nonuniform electromagnetic fields. An expanding plate plasma can be seen in the lower half of the parallel image, and there are caustics caused by electric potentials. The combination of proton deflectometry parallel and perpendicular to the loop axis allows one to differentiate between electric and magnetic fields because the field geometry is different in each orientation. One can check that the electric/magnetic fields required to reproduce an RCF image along one axis are consistent with a different image taken at 
$90^{\circ }$ to the first (see Sections 3.2 and 3.5). Ultimately, this allows us to map the magnetic field evolution and dependence on target parameters such as the loop diameter.
Figure 1. Left: Sample proton radiograph taken perpendicularly to the axis of a 2-mm-diameter wire loop with 
$E_{p}=7.3\pm 0.05~\text{MeV}$ protons. The void width, 
$w$, is proportional to the square root of the current flowing in the coil loop[Reference Gao, Ji, Fiksel, Fox, Evans and Alfonso17], though 
$w$ is also affected by electric fields. Right: Sample proton radiograph taken parallel to the axis of a 1-mm-diameter wire loop with 
$E_{p}=6.5\pm 0.07~\text{MeV}$ protons. Notice how the outline of an Au grid has been imprinted in the proton beam as a fiducial. Each RCF image has a magnification of 
$M=10$, so a distance of 5 mm in the detector plane (indicated above) equates to 0.5 mm in the coil plane.
Since proton deflection in electromagnetic fields depends on the proton energy, 
$E_{p}$, measuring how proton deflection changes on successive layers of RCF may help disentangle the contribution from electric and magnetic fields. According to theory, proton deflection varies weakly with proton energy in a magnetic field (
$\propto E_{p}^{-1/4}$); in an electric field it varies more strongly, as 
$E_{p}^{-1/2}$; for an electric and magnetic field, the deflection will vary as a combination of these two factors, depending on the relative strength of the electric and magnetic fields. Referring to our experimental data, we find that the void diameter varies roughly as 
$E_{p}^{-1/4}$ for several shots where we expect the magnetic field to dominate. At early times, when we expect the electric field to dominate, there is partial agreement with the 
$E_{p}^{-1/2}$ scaling. However, these scalings are not consistent across all shots and layers of RCF. We therefore cannot be conclusive about whether the variation is with 
$E_{p}^{-1/4}$ or 
$E_{p}^{-1/2}$. It may be that the scaling is a combination of these two factors or that the errors in our calculations are too large.
Proton deflectometry has been used in single- and dual-axis configurations to diagnose magnetic fields in laser-heated plasmas[Reference Le Pape, Patel, Chen, Town, Hey and Mackinnon29, Reference Cecchetti, Borghesi, Fuchs, Schurtz, Kar, Macchi, Romagnani, Wilson, Antici, Jung, Osterholtz, Pipahl, Willi, Schiavi, Notley and Neely30] and pulsed power discharges[Reference Manuel, Sinenian, Séguin, Li, Frenje, Rinderknecht, Casey, Zylstra, Petrasso and Beg31, Reference Mariscal, McGuffey, Valenzuela, Wei, Chittenden, Niasse, Presura, Haque, Wallace, Arias, Covington, Sawada, Wiewior and Beg32]. Of these different methods, comparing simultaneous dual-axis images has the clear advantage that it allows one to examine E/B-fields under identical conditions from two directions[Reference Cecchetti, Borghesi, Fuchs, Schurtz, Kar, Macchi, Romagnani, Wilson, Antici, Jung, Osterholtz, Pipahl, Willi, Schiavi, Notley and Neely30]. This is particularly useful if the field geometry is asymmetrical or if there is significant shot-to-shot variation in the laser parameters. We will present our parallel and perpendicular data separately. We found it was not necessary to compare the two axes simultaneously for relatively low wire currents (
$J\leqslant 10~\text{kA}$) because proton deflection in the parallel images was too low to provide an independent measurement of the magnetic field (see Section 4).
All data used to produce the figures in this work, along with other supporting materials, can be found at http://dx.doi.org/10.15124/79ca0a38-dddb-480c-9edf-d8f52496dfad.
2 Experimental setup
Our experiment was conducted on the Vulcan Target Area West (TAW) laser system at the Central Laser Facility. Three ‘long pulse’ beams were used to drive the capacitor coil with a combined energy of 
$E\sim 550~\text{J}$, a pulse duration of 
$t\sim 1~\text{ns}$ (square pulse, 
${\sim}100~\text{ps}$ rise time) and a peak laser intensity of 
$I\sim 5\times 10^{15}~\text{W}\cdot \text{cm}^{-2}$. Two picosecond-duration beams at 
$E\sim 80~\text{J}$ were used for orthogonal TNSA proton radiography[Reference McKenna, Lindau, Lundh, Neely, Persson and Wahlström33] (see Figure 2). All laser beams had wavelengths in the infrared with 
$\unicode[STIX]{x1D706}=1053~\text{nm}$. The capacitor coil targets consisted of two 3-mm-diameter, 250-
$\unicode[STIX]{x03BC}\text{m}$-thick Cu plates separated by 
$500~\unicode[STIX]{x03BC}\text{m}$ and connected by a 100-
$\unicode[STIX]{x03BC}\text{m}$-thick loop of Cu wire. The wire loop had a square cross-section and was laser-cut and joined to the topmost surface of the plates using a conducting adhesive. The front plate contained a 1-mm-diameter hole at the centre to allow the drive lasers access to the rear plate. A 10-
$\unicode[STIX]{x03BC}\text{m}$-thick plastic coating was applied to the rear plate to enhance the nonlinear acceleration of hot electrons[Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody2]. The coil target was supported by a single carbon fibre stalk attached to the rear plate. In Figure 2, there is a photograph and description of the target assembly. TNSA proton beams accelerated off the rear surface of the proton foils passed through Au grids that imprinted a mesh structure into the beam as a visual reference. RCF stacks were then positioned behind the target to detect protons with energies between 
$1.2\pm 0.01~\text{MeV}$ and 
$14\pm 0.1~\text{MeV}$.
Figure 2. Photograph of full capacitor coil target assembly with two proton foils and Au grids. Two rectangular Au foils of 
$40~\unicode[STIX]{x03BC}\text{m}$ thickness with 
$5~\unicode[STIX]{x03BC}\text{m}$ Au shields were used for TNSA proton radiography. Between the proton foils and the capacitor coil, two Au grids were installed to act as visual references in the proton images. RCF stacks were positioned 10 cm behind the target to detect the protons along two axes.
3 Proton deflectometry
3.1 Synthetic proton deflectometry
By comparing the experimental RCF data to synthetic proton radiographs generated using the EPOCH particle-in-cell code[Reference Brady and Arber34], it is possible to estimate the loop current and corresponding magnetic flux density inside a capacitor coil target. Static magnetic fields were calculated for an arbitrary current geometry using a Python finite difference code. These fields were then imported into EPOCH, where a monoenergetic, divergent beam of protons was propagated through the simulation box. Simulations were run on a cubic Cartesian grid, 6 mm wide, with four particles per cell and a grid separation of 
$120~\unicode[STIX]{x03BC}\text{m}$. We disabled the EPOCH field solver so that the protons would respond only to imported electric and magnetic fields. The proton beams had a Gaussian spatial density distribution and linearly increasing divergence up to a maximum value at the beam edge. The maximum divergence angle was calculated based on RCF data taken during the experiment. On exiting the EPOCH simulation box, the proton beam was ballistically extrapolated over a distance of 10 cm into the detector plane and imaged using Python. In some simulations, vertical and horizontal lines were cut out of the initial proton distribution to act as fiducials, mimicking the Au grids that were imprinted on the experimental RCF data (see Figures 1 and 2).
3.2 Perpendicular deflectometry: B-field-only simulations
Simulated radiographs of protons passing perpendicularly across a static capacitor coil magnetic field are shown in Figure 3. No electric fields were included in these simulations. Comparison with the RCF data suggests that currents in both the 1-mm- and 2-mm-diameter loops were equal to 
$J\sim 5~\text{kA}$, 
$t>800~\text{ps}$ after the arrival of the nanosecond drive beams, with corresponding magnetic fields at the loop centre of 
$B\sim 6~\text{T}$ and 
$B\sim 3~\text{T}$, respectively. At early times (
$t\sim 0.3~\text{ns}$), the proton voids are significantly larger and equate to loop currents above 
$J=10~\text{kA}$. The 1-mm-diameter loops had a peak current of 
$J<14~\text{kA}$ at 
$t=0.3~\text{ns}$ after laser drive, which corresponds to a B-field of 
$B<18~\text{T}$ at the loop centre; the 2-mm-diameter loops had a peak current of 
$J<10~\text{kA}$ and a B-field of 
$B<6~\text{T}$ at the same time. These early measurements were taken off-axis (due to misalignment of the capacitor coil target), which means the protons would have passed through a more extended magnetic field and may feature artificially large proton voids. Comparison with axial radiography suggests that the peak B-field actually occurs later in time, at 
$t>0.8~\text{ns}$, and that electric fields may be responsible for large proton deflections soon after the beginning of the laser drive (see Sections 3.3 and 3.5). Measurements of the magnetic field between 
$t=0.8~\text{ns}$ and 
$t=1.5~\text{ns}$ suggest that the current remains stable at 
$J=5{-}10~\text{kA}$ for several hundred picoseconds.
Figure 3. Comparison of EPOCH simulations with RCF data for (a) 1-mm- and (b) 2-mm-diameter capacitor coil loops. EPOCH simulations used a monoenergetic 
$E_{p}=7~\text{MeV}$ proton beam with a divergence angle of 
$40^{\circ }$. The RCF data shown corresponds to protons with energy 
$E_{p}=7.3\pm 0.05~\text{MeV}$. Proton voids are bigger at early times (
$t\sim 0.3~\text{ns}$) before decaying to a stable value for 
$t>0.8~\text{ns}$. Estimated loop currents at 
$t>0.8~\text{ns}$ are 
$J=5~\text{kA}$ for both loop diameters. The magnification of each RCF image is 
$M=10$, so a distance of 5 mm in the detector plane (indicated above) equates to 0.5 mm in the coil plane.
Figure 4. Left: Experimental RCF data for a 1-mm-diameter loop taken at 
$t\sim 0.8~\text{ns}$ with 
$E_{p}=7.3\pm 0.05~\text{MeV}$ protons. Right: Synthetic proton radiograph for 7 MeV protons passing across a 1-mm-diameter loop with capacitor-coil-shaped B-field and a uniformly charged circular ring. Note that the loop current that best matches the RCF data is now three times higher than that in Figure 3 (
$J=15~\text{kA}$ versus 
$J=5~\text{kA}$). Horizontal and vertical lines are provided as fiducials. The magnification of each RCF image is 
$M=10$, so a distance of 5 mm in the detector plane (indicated above) equates to 0.5 mm in the coil plane.
Figure 5. Demonstration of the effect of positive wire electric fields on proton void structure. In these deflectometry simulations, 7 MeV protons were propagated perpendicularly across a 1-mm-diameter wire loop. Horizontal and vertical lines have been cut out of the proton distribution to act as fiducials. Left: Simulation run with electric fields only. Electric fields were calculated for a uniformly charged wire loop with total charge 
$Q=10~\text{nC}$. Proton displacement is approximately constant across the entire length of the wire. Distortion of the fiducial grid is only observed near the top of the loop – not near the vertical wire sections. Right: Simulation run with electric and magnetic fields. Electric fields were calculated for a uniformly charged wire loop with total charge 
$Q=5~\text{nC}$, while magnetic fields were generated from a uniform wire current of 
$J=5~\text{kA}$. The proton void width is 6 mm – approximately 1 mm larger than that observed for the same simulation without an electric field.
Figure 6. (a) Axial proton radiograph for a 2-mm-diameter loop, 
$t\sim 0.8~\text{ns}$ after the beginning of the laser drive. Image taken using 
$E_{p}=7.3\pm 0.05~\text{MeV}$ protons. Two areas have been highlighted with white circles: Region 1, axial proton void at the centre of the capacitor coil loop; Region 2, grid distortion is concentrated at the base of the vertical wires and around the plates. (b) Synthetic proton radiograph for a circular ring of current (
$J=40~\text{kA}$) with an overlapped circular ring of charge (
$Q=-80~\text{nC}$). (c) Synthetic proton radiograph for a capacitor coil wire carrying 
$J=40~\text{kA}$ with an overlapped uniform charge distribution (
$Q=-110~\text{nC}$). Each RCF image is magnified by a factor 
$M=10$, so a distance of 5 mm in the detector plane (indicated above) equates to 0.5 mm in the coil plane. Insets in the bottom right hand corner of (b) and (c) are diagrams of the conductor geometry used in each simulation.
3.3 Perpendicular deflectometry: combined E- and B-field simulations
An accumulation of negative charge in the vicinity of the wire loop could produce strong electric fields that reduce the size of the proton void generated by the magnetic fields. Thus simulations that include negative electric charges can predict higher loop currents than simulations with just a magnetic field alone[Reference Santos, Bailly-Grandvaux, Ehret, Arefiev, Batani, Beg, Calisti, Ferri, Florido, Forestier-Colleoni, Fujioka, Gigosos, Giuffrida, Gremillet, Honrubia, Kojima, Korneev, Law, Marquès, Morace, Mossé, Peyrusse, Rose, Roth, Sakata, Schaumann, Suzuki-Vidal, Tikhonchuk, Toncian, Woolsey and Zhang8]. A spherical charge distribution placed near the wire loop and Cu plates produced unrepresentative synthetic radiographs, so we have chosen to study two alternative charge geometries: a circular ring and a capacitor coil loop. In Figure 4, we present a synthetic proton radiograph made with a uniform, negatively charged circular ring and a current in the experimental wire geometry. The inferred current for a 1-mm-diameter loop with 
$Q=-10~\text{nC}$ charge is 
$J=15~\text{kA}$ – three times larger than that for the B-field-only simulations. Possible explanations for this ring of negative charge include: a cloud of hot electrons that have been ejected from the laser focal spot and become trapped in the capacitor coil fields or a build-up of negative charge maintained by the target capacitance. The geometric capacitance of our capacitor coil plates is 
$C=0.1~\text{pF}$, so for an inter-plate voltage of 
$V=30{-}50~\text{kV}$ the coil may accumulate a charge of magnitude 
$Q=CV\sim 3{-}5~\text{nC}$ distributed over the wire surface.
Charge separation in the laser focal spot will generate a positive potential that spreads out over the capacitor coil plates and connecting wire[Reference Poyé, Hulin, Bailly-Grandvaux, Dubois, Ribolzi, Raffestin, Bardon, Lubrano-Lavaderci, D’Humières, Santos, Nicolaï and Tikhonchuk21, Reference Wang, Cai, Teng, Chen, He, Shan, Lu, Wu, Zhang, Hong, Bi, Zhang, Liu, Xue, Li, Liu, He, Jiao, Dong, Zhang, He, Cui, Xie, Yuan, Tian, Wang, Zhou, Deng, Zhang, Zhou, Cao, Zhang, Zhu, He and Gu28, Reference Quinn, Wilson, Cecchetti, Ramakrishna, Romagnani, Sarri, Lancia, Fuchs, Pipahl, Toncian, Willi, Clarke, Neely, Notley, Gallegos, Carroll, Quinn, Yuan, McKenna, Liseykina, Macchi and Borghesi35, Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi36]. A positively charged wire acts to deflect protons radially away from the wire surface. These protons are deflected outwards by a similar amount all along the wire, so positive electric fields cannot reproduce a teardrop-shaped void without magnetic fields. Electric fields can, however, increase the width of the proton void generated by a magnetic field as well as the apparent thickness of the vertical wire sections (see Figure 5). Comparing the simulated vertical wire thickness with RCF images for 
$t>0.5~\text{ns}$, we find upper limits on the positive wire charge and electric field of 
$Q\sim 5~\text{nC}$ and 
$E\sim 1\times 10^{8}~\text{V}\cdot \text{m}^{-1}$, respectively. This electric field is too small to significantly affect the measured teardrop void diameter and inferred current. A peak current of a few kiloamperes is still valid in simulations with electric fields of 
$E\sim 1\times 10^{8}~\text{V}\cdot \text{m}^{-1}$ at the wire surface.
The larger the electrostatic charge, the stronger the grid deflection around the loop. In Section 3.4, we will examine grid deflection in axial RCF images in order to estimate the likely charge geometry and amplitude.
3.4 Axial deflectometry: negative charge distribution
Grid deflection in the axial proton images can provide information about the likely charge distribution present around the target – essential for accurate simulations of proton deflectometry. Figure 6(a) shows a typical axial proton radiograph for a 2-mm-diameter capacitor coil loop. At the centre of the loop, inside the region labelled 1, there is an area of low proton signal. EPOCH simulations with a uniformly charged ring and a uniformly charged capacitor coil wire both produce proton void shapes for total charges 
$Q=-80~\text{nC}$ and 
$Q=-110~\text{nC}$, respectively (see Figures 6(b) and 6(c)). These are not true ‘voids’, however, because the on-axis proton density has not decreased. Simulations also show enhanced proton signal between the negatively charged wires, which is not supported by experiment.
In Figure 7, strong grid deflection is observed around a 1 mm loop for a loop charge of 
$Q\sim -40~\text{nC}$; this is much greater than that observed in the RCF data. Instead, grid deflection is concentrated around the plate region on the RCF, which suggests that 
$Q\sim -10~\text{nC}$ can be seen as a likely upper limit on the quantity of negative charge present in the loop (see Figures 6(a) and 7(b)). This charge corresponds to a maximum probable current of 
$J=15~\text{kA}$ (
$B\sim 19~\text{T}$) and does not explain the axial proton void.
Figure 7. Synthetic proton radiographs for a 1-mm-diameter charged ring on top of a capacitor coil loop carrying a current 
$J=15~\text{kA}$. Vertical and horizontal lines have been cut out of the proton beam to act as fiducials. (a) Grid deflection is minimal around the loop for B-field simulations with a static current. (b) For 
$Q=-10~\text{nC}$, we see millimetre-scale grid deflections consistent with the RCF data. (c) For 
$Q=-40~\text{nC}$, grid deflection is of centimetre scale and much larger than that observed on the RCF.
3.5 Axial deflectometry: upper limits on capacitor coil magnetic field
EPOCH simulations of protons passing through a current loop suggest that the beam will rotate as it passes through the magnetic field (clockwise or anticlockwise depending on the polarization of the current). Thus if a fiducial (e.g., high-
$Z$ metallic grid) is inserted between the proton foil and the capacitor coil target, the imprint of the fiducial in the proton image will twist as a function of the applied magnetic field[Reference Wang, Cai, Teng, Chen, He, Shan, Lu, Wu, Zhang, Hong, Bi, Zhang, Liu, Xue, Li, Liu, He, Jiao, Dong, Zhang, He, Cui, Xie, Yuan, Tian, Wang, Zhou, Deng, Zhang, Zhou, Cao, Zhang, Zhu, He and Gu28] (see Figure 8). This effect is analogous to a proton gyrating around magnetic field lines. In Figure 8(b), the straight line represents protons rotating at their gyrofrequency in a 1-mm-scale uniform magnetic field. The magnitude of the magnetic field is taken to be 
$B=\unicode[STIX]{x1D707}_{0}J/2R$, where 
$J$ is the loop current and 
$R$ the loop radius. It is important to note that the beam rotation angle is not significantly affected by electric fields or proton beam divergence, making this a reliable measure of the loop magnetic field (see Figure 9). The RCF data does not show any evidence of a fixed rotation angle inside the loop, which suggests that the wire current is below 
$J=10~\text{kA}$ for all loop diameters.
Figure 8. (a) Synthetic radiograph for a 7 MeV divergent proton beam passing through the magnetic field of a 2-mm-diameter current loop carrying a current 
$J=100~\text{kA}$. A vertical slot is cut out of the Gaussian proton distribution, which rotates through an approximately fixed 
$13^{\circ }$ angle inside the loop. (b) Blue points: graph of loop current plotted against rotation angle of the fiducial grid for a 2-mm-diameter current loop. Since there is no evidence of grid rotation in the RCF data, this puts an upper limit on the loop current of less than 
$J=10~\text{kA}$. The straight line represents proton gyration angle for protons passing perpendicularly through a uniform magnetic field of 1 mm spatial scale. The magnitude of this magnetic field is equivalent to the B-field at the centre of a 2-mm-diameter current loop.
Figure 9. (a) Study of grid rotation with different loop charges. Negative charge is distributed uniformly along the capacitor coil loop and the proton beam divergence angle is fixed at 
$40^{\circ }$. We can see that the angle of rotation of the grid is unchanged for different loop charges. (b) Proton beam with zero divergence passing through the magnetic field of a current loop carrying 
$J=40~\text{kA}$ – the grid rotation angle is unchanged versus the 
$40^{\circ }$ case.
Grid deflection close to the wire surface can also be used as a measure of the wire current and magnetic field. The vertical wires under the capacitor coil loop provide a simplified geometry for conducting simulations of the magnetic field. Figure 10 shows a simulation of two infinitesimally thin current-carrying wires – the wires are placed in parallel with opposite polarizations. For currents 
$J>15~\text{kA}$, we would expect significant (multi-millimetre) deflections close to the wire surface. This is hard to diagnose on the RCF due to poor grid resolution, though a smeared-out region around the wire, 
${\sim}1{-}2~\text{mm}$ wide, puts a maximum estimate of the wire current at approximately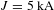 
$J=5~\text{kA}$ (see Figure 10(c)). The origin of this smeared-out region is not certain. At early times (
$t\,<\,0.4~\text{ns}$), the smearing is very clearly defined and may be caused by positive charging of the wire (up to 
$Q\sim 10~\text{nC}$), giving an apparent wire thickness two to three times larger than a wire with no laser drive[Reference Quinn, Wilson, Cecchetti, Ramakrishna, Romagnani, Sarri, Lancia, Fuchs, Pipahl, Toncian, Willi, Clarke, Neely, Notley, Gallegos, Carroll, Quinn, Yuan, McKenna, Liseykina, Macchi and Borghesi35, Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi36]. The smearing generally has a smaller spatial extent at later times (
$t>0.8~\text{ns}$) and is less uniform.
Figure 10. (a) Magnetic field geometry used in simulations of two vertical wires with opposite currents. (b) Synthetic radiograph for two vertical wires carrying 
$J=\pm 20~\text{kA}$. Horizontal fiducial demonstrates multi-millimetre grid deflection close to the wire surface. Approximate location of the wire surface is picked out with vertical dashed lines. (c) Detail from RCF image of 1-mm-diameter loop taken 
$t\sim 0.8~\text{ns}$ after the beginning of the laser drive. Though there is no clear evidence of a continuous grid deflection around the vertical wires, a smeared-out region 
${\sim}1{-}2~\text{mm}$ thick around the wire puts an upper limit on the wire current at 
$J\sim 5~\text{kA}$.
4 Discussion
Comparing synthetic proton radiographs with a range of current and charge distributions is necessary to place upper and lower limits on the capacitor coil magnetic field. EPOCH simulations show that negative charges around the wire allow us to infer larger loop currents, but there is no experimental evidence for this effect in the axial RCF data. Enhanced current estimates of 
$J=10{-}15~\text{kA}$ are contradicted by axial grid rotation measurements, and spherical charge distributions are likewise ruled out by simulations. Naturally, this does not exclude electron clouds having a significant impact on B-field estimates for different capacitor coil targets, where the loop is positioned closer to the laser focal spot[Reference Santos, Bailly-Grandvaux, Ehret, Arefiev, Batani, Beg, Calisti, Ferri, Florido, Forestier-Colleoni, Fujioka, Gigosos, Giuffrida, Gremillet, Honrubia, Kojima, Korneev, Law, Marquès, Morace, Mossé, Peyrusse, Rose, Roth, Sakata, Schaumann, Suzuki-Vidal, Tikhonchuk, Toncian, Woolsey and Zhang8]. Positive wire charging can explain proton deflection away from the wires at early times (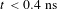
$t<0.4~\text{ns}$) as well as the absence of grid distortion, but measurements suggest that positive electric fields do not have a significant impact on estimates of the wire current for 
$t>0.5~\text{ns}$. Combining upper estimates of the wire electric field with measurements of axial grid rotation and perpendicular proton void width, we conclude that peak currents of 
$J=3{-}5~\text{kA}$ were achieved in both the 1- and 2-mm-diameter capacitor coils.
The approximate magnetic field energy for the 1-mm-diameter targets is given by 
$E_{B}=\frac{1}{2}LJ^{2}\sim 0.15~\text{J}$ (
$L$ is the loop inductance and 
$J$ is the wire current), which corresponds to a laser energy conversion efficiency of 
${\sim}0.03\%$. This is 
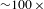${\sim}100\,\times \,$ lower than that quoted for experiments at LULI[Reference Santos, Bailly-Grandvaux, Ehret, Arefiev, Batani, Beg, Calisti, Ferri, Florido, Forestier-Colleoni, Fujioka, Gigosos, Giuffrida, Gremillet, Honrubia, Kojima, Korneev, Law, Marquès, Morace, Mossé, Peyrusse, Rose, Roth, Sakata, Schaumann, Suzuki-Vidal, Tikhonchuk, Toncian, Woolsey and Zhang8, Reference Santos, Bailly-Grandvaux, Giuffrida, Forestier-Colleoni, Fujioka, Zhang, Korneev, Bouillaud, Dorard, Batani, Chevrot, Cross, Crowston, Dubois, Gazave, Gregori, d’Humières, Hulin, Ishihara, Kojima, Loyez, Marquès, Morace, Nicolaï, Peyrusse, Poyé, Raffestin, Ribolzi, Roth, Schaumann, Serres, Tikhonchuk, Vacar and Woolsey16], though the discrepancy can be explained by a lower hot electron temperature. On Vulcan, we were operating at 
$20\,\times \,$ lower intensity than LULI, and
$T_{e}=T_{e}(I\unicode[STIX]{x1D706}^{2})$ is an important parameter governing the loop current in theoretical models of capacitor coils[Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody2, Reference Tikhonchuk, Bailly-Grandvaux, Santos and Poyé6, Reference Fiksel, Fox, Gao and Ji37].
The hot electron temperature achieved in the laser focal spot can be estimated from the Forslund 
$I\unicode[STIX]{x1D706}^{2}$ scaling for a laser interacting with a steep plasma density gradient[Reference Forslund, Kindel and Lee38]. For our experimental parameters, this gives a value of
$T_{e}\sim 14~\text{keV}$. Although we used a layer of CH plastic to try to enhance the hot electron temperature, the measured current/magnetic field was actually slightly lower when using plastic coated targets. Since the loop current is thought to vary sensitively with 
$T_{e}$[Reference Goyon, Pollock, Turnbull, Hazi, Divol, Farmer, Haberberger, Javedani, Johnson, Kemp, Levy, Logan, Mariscal, Landen, Patankar, Ross, Rubenchik, Swadling, Williams, Fujioka, Law and Moody2, Reference Tikhonchuk, Bailly-Grandvaux, Santos and Poyé6, Reference Fiksel, Fox, Gao and Ji37], this suggests that the plastic layer did not increase the hot electron temperature. We note that 
$T_{e}$ was not measured directly during the experiment.
Based on a laser-diode model of the capacitor coil target[Reference Tikhonchuk, Bailly-Grandvaux, Santos and Poyé6], for a hot electron temperature of 
$T_{e}\sim 14~\text{keV}$, wire inductance 
$L=10~\text{nH}$ and wire resistance 
$R=1~\unicode[STIX]{x03A9}$, we should be able to produce a maximum potential of around 
$V=2T_{e}{-}3T_{e}=30{-}50~\text{kV}$ between the plates. The current rise time is 
$V/L=\text{d}J/\text{d}t\sim 3{-}5~\text{kA}$/ns, which is in agreement with the experimental value of 
$J\sim 5~\text{kA}$ at 
$t>0.5~\text{ns}$. Looking towards future experiments with capacitor coils, this conclusion supports the laser-diode model[Reference Tikhonchuk, Bailly-Grandvaux, Santos and Poyé6] and suggests that 
$B\sim 100~\text{T}$ magnetic fields can be attained at high laser intensity (
$I=10^{16}{-}10^{17}~\text{W}\cdot \text{cm}^{-2}$) with submillimetre-diameter wire loops.
5 Conclusion
In summary, we have demonstrated dual-axis proton probing of the electromagnetic fields around a capacitor coil target at a laser drive intensity of 
$I\sim 5\times 10^{15}~\text{W}\cdot \text{cm}^{-2}$. The chief advantage of dual-axis proton deflectometry is that an upper limit can be placed on the magnetic flux density independent of electric fields using grid rotation measurements along the loop axis. When this is combined with measurements of the perpendicular void diameter and apparent wire thickness, a reliable estimate of the magnetic field can be extracted. Particle-in-cell simulations with a static magnetic field suggest that we achieved peak loop currents of 
$J\sim 5~\text{kA}$ at 
$t>0.8~\text{ns}$ for both 1-mm- and 2-mm-diameter loops, with corresponding magnetic fields of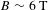 
$B\sim 6~\text{T}$ and 
$B\sim 3~\text{T}$ at the loop centre. Simulations with electric and magnetic fields show that these current estimates are sensitive to concentrations of positive and negative charges around the capacitor coil. Evidence for electric charges in the target comes from localized distortion of the fiducial grid. The absence of grid rotation inside the loop implies a maximum wire current of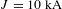 
$J=10~\text{kA}$, while the absence of significant grid deflections close to the wire surface suggests that the current cannot exceed 
$J\sim 5~\text{kA}$. Taking into account an upper limit on the positive charge on the wire, we conclude that currents of 
$J=3{-}5~\text{kA}$ were achieved using 1-mm- and 2-mm-diameter capacitor coils. Estimated values for the current and magnetic field agree well with predictions from a laser-driven diode model. The simulations in this paper were run with static uniform currents and uniform charge distributions – they do not account for dynamic, non-uniform currents and charges around the target. Future work will look at more comprehensive simulations of the wire current spatial profile and charge geometry.
Acknowledgements
The authors would like to thank the Central Laser Facility staff, whose dedication and expertise were essential to the success of their experiment. This paper was supported by the LLNL Academic Partnership in ICF, EPSRC grants EP/L01663X/1 and EP/L000644/1 and the Czech Republic MSMT targeted support of Large Infrastructures, ELI Beamlines Project LQ1606 of the National Programme of Sustainability II. The authors have also received funding from the EUROfusion Consortium via Euratom research and training programme 2014–2018 under grant agreement No. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. The contribution of the JIHT RAS team was completed within the framework of the Russian Ministry state assignment for Science and Higher Education (topic #01201357846). M. P. Read is currently based at First Light Fusion, Oxford Industrial Park, Kidlington, OX5 1QU, UK.
Open access
