Hostname: page-component-7479d7b7d-767nl Total loading time: 0 Render date: 2024-07-12T15:06:51.857Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimizing the learning loss in adaptive control of Markov chains under the weak accessibility condition

Published online by Cambridge University Press:  14 July 2016

Rajeev Agrawal
Rajeev Agrawal*
Affiliation:
University of Wisconsin-Madison
*
∗ Postal address: Department of Electrical and Computer Engineering, University of Wisconsin-Madison, Madison, WI 53706–1691, USA. E-mail: agrawal@engr.wisc.edu.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the adaptive control of Markov chains under the weak accessibility condition with a view to minimizing the learning loss. A certainty equivalence control with a forcing scheme is constructed. We use a stationary randomized control scheme for forcing and compute a maximum likelihood estimate of the unknown parameter from the resulting observations. We obtain an exponential upper bound on the rate of decay of the probability of error. This allows us to choose the rate of forcing appropriately, whereby we achieve a o(f(n) log n) learning loss for any function 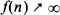as .

Keywords

CONTROLLED MARKOV CHAINSSTOCHASTIC ADAPTIVE CONTROLCERTAINTY EQUIVALENCE CONTROLFORCINGLEARNING LOSS
Type
Research Papers
Information
Journal of Applied Probability , Volume 28 , Issue 4 , December 1991 , pp. 779 - 790
Copyright
Copyright © Applied Probability Trust 1991 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by NSF Grant No. ECS-8919818.

References

[1] Agrawal, R., Hegde, M. and Teneketzis, D. (1988) Asymptotically efficient adaptive allocation rules for the multi-armed bandit problem with switching cost. IEEE Trans. Autom. Control 33, 899–906.10.1109/9.7243Google Scholar
[2] Agrawal, R. and Teneketzis, D. (1989) Certainty equivalence control with forcing: Revisited. Syst. Contr. Lett. 13, 405–412.10.1016/0167-6911(89)90107-2Google Scholar
[3] Agrawal, R., Teneketzis, D. and Anantharam, V. (1989) Asymptotically efficient adaptive allocation schemes for controlled Markov chains: Finite parameter space. IEEE Trans. Autom. Contr. 34, 1249–1259.10.1109/9.40770Google Scholar
[4] Anantharam, V., Varaiya, P. and Walrand, J. (1987) Asymptotically efficient allocation rules for the mutiarmed bandit problem with multiple plays; Part I: IID rewards. IEEE Trans. Autom. Control. 32, 968–975.10.1109/TAC.1987.1104491Google Scholar
[5] Anantharam, V., Varaiya, P. and Walrand, J. (1987) Asymptotically efficient allocation rules for the mutiarmed bandit problem with multiple plays; Part II: Markovian rewards. IEEE Trans. Autom. Control. 32, 975–982.Google Scholar
[6] Bather, J. (1973) Optimal decision procedures for finite Markov chains. Part II: Communicating systems. Adv. Appl. Prob. 5, 521–540.10.2307/1425832Google Scholar
[7] Bertsekas, D. P. (1976) Dynamic Programming and Stochastic Control. Academic Press, New York.Google Scholar
[8] Ellis, R. (1985) Entropy, Large Deviations, and Statistical Mechanics. Springer-Verlag, Berlin.10.1007/978-1-4613-8533-2Google Scholar
[9] Kumar, P. R. (1985) A survey of some results in stochastic adaptive control. SIAM J. Control Optim. 23, 329–380.10.1137/0323023Google Scholar
[10] Kumar, P. R. and Varaiya, P. (1986) Stochastic Systems: Estimation, Identification and Adaptive Control. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
[11] Lai, T. L. and Robbins, H. (1985) Asymptotically efficient adaptive allocation rules. Adv. Appl. Math. 6, 4–22.10.1016/0196-8858(85)90002-8Google Scholar
[12] Robbins, H. (1952) Some aspects of sequential design of experiments. Bull. Amer. Math. Soc. 55, 527–535.10.1090/S0002-9904-1952-09620-8Google Scholar
[13] Schweitzer, P. J. (1968) Perturbation theory and finite Markov chains. J. Appl. Prob. 5, 401–413.10.2307/3212261Google Scholar