Hostname: page-component-5c6d5d7d68-pkt8n Total loading time: 0 Render date: 2024-08-15T02:17:40.905Z Has data issue: false hasContentIssue false
  • English
  • Français

On the age distribution of a Markov chain

Published online by Cambridge University Press:  14 July 2016

Anthony G. Pakes
Anthony G. Pakes*
Affiliation:
Monash University, Clayton, Victoria
Get access Rights & Permissions [Opens in a new window]

Abstract

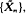This paper develops the notion of the limiting age of an absorbing Markov chain, conditional on the present state. Chains with a single absorbing state {0} are considered and with such a chain can be associated a return chain, obtained by restarting the original chain at a fixed state after each absorption. The limiting age, A(j), is the weak limit of the time 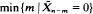given Xn = j (n → ∞).

A criterion for the existence of this limit is given and this is shown to be fulfilled in the case of the return chains constructed from the Galton–Watson process and the left-continuous random walk. Limit theorems for A (J) (J → ∞) are given for these examples.

Keywords

MARKOV CHAINRETURN CHAINSTRONG RATIO LIMIT PROPERTYR-CLASSIFICATIONGALTON—WATSON PROCESSLEFT-CONTINUOUS RANDOM WALKLIMIT THEOREMSLOCAL LIMIT THEOREMS
Type
Research Papers
Information
Journal of Applied Probability , Volume 15 , Issue 1 , March 1978 , pp. 65 - 77
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Chung, K. L. (1967) Markov Chains with Stationary Probabilities, 2nd edn. Springer-Verlag, Berlin.Google Scholar
Dubuc, S. (1970) La fonction de Green d'un processus de Galton-Watson. Studia Math. 34, 69–87.Google Scholar
Dubuc, S. (1971) La densité de la loi-limite d'un processus en cascade expansif. Z. Wahrscheinlichkeitsth. 19, 281–290.CrossRefGoogle Scholar
Erickson, K. B. (1970) Strong renewal theorems with infinite mean. Trans. Amer. Math. Soc. 151, 263–291.Google Scholar
Folkman, J. H. and Port, S. C. (1966) On Markov chains with the strong ratio limit property. J. Math. Mech. 15, 113–122.Google Scholar
Foster, J. (1971) A limit theorem for a branching process with state-dependent immigration. Ann. Math. Statist. 42, 1773–1776.Google Scholar
Garsia, A. (1963) Some Tauberian theorems and the asymptotic behaviour of recurrent events. J. Math. Anal. Appl. 7, 146–162.Google Scholar
Garsia, A. and Lamperti, J. (1962) A discrete renewal theorem with infinite mean. Comment. Math. Helv. 37, 221–234.Google Scholar
Garsia, A., Orey, S. and Rodemich, E. (1962) Asymptotic behaviour of the successive coefficients of some power series. Ill. J. Math. 6, 620–629.Google Scholar
Ibragimov, I. A. and Linnik, Yu. (1971) Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff, Groningen.Google Scholar
Kaigh, W. D. (1975) A conditional local limit theorem for recurrent random walk. Ann. Prob. 3, 883–888.Google Scholar
Kingman, J. F. C. (1972) Regenerative Phenomena. Wiley, London.Google Scholar
Kingman, J. F. C. and Orey, S. (1964) Ratio limit theorems for Markov chains. Proc. Amer. Math. Soc. 15, 907–910.Google Scholar
Levikson, B. (1977) The age distribution of Markov processes. J. Appl. Prob. 14, 492–506.CrossRefGoogle Scholar
Pakes, A. G. (1971) A branching process with a state-dependent immigration component. Adv. Appl. Prob. 3, 301–314.Google Scholar
Pakes, A. G. (1973) Conditional limit theorems for a left-continuous random walk. J. Appl. Prob. 10, 39–53.Google Scholar
Pares, A. G. (1975) Some results for non-supercritical Galton-Watson processes with immigration. Math. Biosci. 25, 71–92.Google Scholar
Pares, A. G. and Speed, T. P. (1977) Lagrange distributions and their limit theorems. Siam. J. Appl. Math. 32, 745–754.Google Scholar
Pegg, P. A. and Phatarfod, R. M. (1977) Dams with additive inputs revisited. J. Appl. Prob. 14, 367–374.Google Scholar
Pruitt, W. E. (1965) Strong ratio limit property for R-recurrent Markov chains. Proc. Amer. Math. Soc. 17, 196–200.Google Scholar
Seneta, E. (1967) The Galton-Watson process with mean one. J. Appl. Prob. 4, 489–495.Google Scholar
Seneta, E. (1969) Functional equations and the Galton-Watson process. Adv. Appl. Prob. 1, 1–42.Google Scholar
Seneta, E. (1973) Non-Negative Matrices. Allen and Unwin, London.Google Scholar
Williamson, J. A. (1968) Random walks and Riesz kernels. Pacific J. Math. 25, 393–415.Google Scholar