Hostname: page-component-84b7d79bbc-dwq4g Total loading time: 0 Render date: 2024-08-02T07:23:13.009Z Has data issue: false hasContentIssue false
  • English
  • Français

On the speed of convergence of discrete Pickands constants to continuous ones

Part of: Probabilistic methods, simulation and stochastic differential equations Stochastic processes

Published online by Cambridge University Press:  31 July 2024

Krzysztof Bisewski  and
Grigori Jasnovidov
Krzysztof Bisewski*
Affiliation:
University of Lausanne
Grigori Jasnovidov*
Affiliation:
Russian Academy of Sciences
*
*Postal address: UNIL-Dorigny, 1015 Lausanne, Switzerland. Email address: kbisewski@gmail.com
**Postal address: St. Petersburg Department of Steklov Mathematical Institute of Russian Academy of Sciences, 27 Fontanka, 191023, St. Petersburg, Russia. Email address: griga1995@yandex.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

In this manuscript, we address open questions raised by Dieker and Yakir (2014), who proposed a novel method of estimating (discrete) Pickands constants 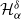$\mathcal{H}^\delta_\alpha$ using a family of estimators 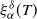$\xi^\delta_\alpha(T)$, 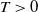$T>0$, where 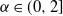$\alpha\in(0,2]$ is the Hurst parameter, and 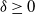$\delta\geq0$ is the step size of the regular discretization grid. We derive an upper bound for the discretization error 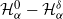$\mathcal{H}_\alpha^0 - \mathcal{H}_\alpha^\delta$, whose rate of convergence agrees with Conjecture 1 of Dieker and Yakir (2014) in the case 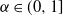$\alpha\in(0,1]$ and agrees up to logarithmic terms for 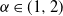$\alpha\in(1,2)$. Moreover, we show that all moments of 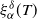$\xi_\alpha^\delta(T)$ are uniformly bounded and the bias of the estimator decays no slower than 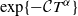$\exp\{-\mathcal CT^{\alpha}\}$, as T becomes large.

Keywords

Fractional Brownian motionPickands constantsMonte Carlo simulationdiscretization error

MSC classification

Primary: 60G15: Gaussian processes
Secondary: 60G70: Extreme value theory; extremal processes 65C05: Monte Carlo methods
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 25
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albin, J. M. P. and Choi, H. (2010). A new proof of an old result by Pickands. Electron. Commun. Prob. 15, 339–345.CrossRefGoogle Scholar
Aurzada, F., Buck, M. and Kilian, M. (2020). Penalizing fractional Brownian motion for being negative. Stoch. Process. Appl. 130, 6625–6637.CrossRefGoogle Scholar
Bai, L., Dębicki, K., Hashorva, E. and Luo, L. (2018). On generalised Piterbarg constants. Methodology Comput. Appl. Prob. 20, 137–164.CrossRefGoogle Scholar
Bisewski, K., Hashorva, E. and Shevchenko, G. (2023). The harmonic mean formula for random processes. Stoch. Anal. Appl. 41, 591–603.CrossRefGoogle Scholar
Bisewski, K. and Ivanovs, J. (2020). Zooming-in on a Lévy process: failure to observe threshold exceedance over a dense grid. Electron. J. Prob. 25, paper no. 113, 33 pp.Google Scholar
Bisewski, K. and Jasnovidov, G. (2023). On the speed of convergence of Piterbarg constants. Queueing Systems 105, 129–137.CrossRefGoogle Scholar
Borovkov, K., Mishura, Y., Novikov, A. and Zhitlukhin, M. (2017). Bounds for expected maxima of Gaussian processes and their discrete approximations. Stochastics 89, 21–37.CrossRefGoogle Scholar
Borovkov, K., Mishura, Y., Novikov, A. and Zhitlukhin, M. (2018). New and refined bounds for expected maxima of fractional Brownian motion. Statist. Prob. Lett. 137, 142–147.CrossRefGoogle Scholar
Cvijović, D. (2007). New integral representations of the polylogarithm function. Proc. R. Soc. London A 463, 897–905.CrossRefGoogle Scholar
Dalang, R. et al. (2009). A Minicourse on Stochastic Partial Differential Equations. Springer, Berlin.Google Scholar
Dębicki, K. (2002). Ruin probability for Gaussian integrated processes. Stoch. Process. Appl. 98, 151–174.CrossRefGoogle Scholar
Dębicki, K. (2005). Some properties of generalized Pickands constants. Teor. Veroyat. Primen. 50, 396–404.CrossRefGoogle Scholar
Dębicki, K., Engelke, S. and Hashorva, E. (2017). Generalized Pickands constants and stationary max-stable processes. Extremes 20, 493–517.CrossRefGoogle Scholar
Dębicki, K. and Hashorva, E. (2017). On extremal index of max-stable stationary processes. Prob. Math. Statist. 37, 299–317.Google Scholar
Dębicki, K., Hashorva, E. and Ji, L. (2015). Parisian ruin of self-similar Gaussian risk processes. J. Appl. Prob. 52, 688–702.CrossRefGoogle Scholar
Dębicki, K., Hashorva, E. and Ji, L. (2016). Parisian ruin over a finite-time horizon. Sci. China Math. 59, 557–572.CrossRefGoogle Scholar
Dębicki, K., Hashorva, E. and Michna, Z. (2021). On the continuity of Pickands constants. Preprint. Available at https://arxiv.org/abs/2105.10435.Google Scholar
Dębicki, K., Liu, P. and Michna, Z. (2020). Sojourn times of Gaussian processes with trend. J. Theoret. Prob. 33, 2119–2166.CrossRefGoogle Scholar
Dębicki, K. and Mandjes, M. (2015). Queues and Lévy Fluctuation Theory. Springer, Cham.CrossRefGoogle Scholar
Dębicki, K., Michna, Z. and Peng, X. (2019). Approximation of sojourn times of Gaussian processes. Methodology Comput. Appl. Prob. 21, 1183–1213.CrossRefGoogle Scholar
Dieker, A. B. (2005). Extremes of Gaussian processes over an infinite horizon. Stoch. Process. Appl. 115, 207–248.CrossRefGoogle Scholar
Dieker, A. B. and Mikosch, T. (2015). Exact simulation of Brown–Resnick random fields at a finite number of locations. Extremes 18, 301–314.CrossRefGoogle Scholar
Dieker, A. B. and Yakir, B. (2014). On asymptotic constants in the theory of extremes for Gaussian processes. Bernoulli 20, 1600–1619.CrossRefGoogle Scholar
Dieker, T. (2004). Simulation of fractional Brownian motion. Doctoral Thesis, University of Twente.Google Scholar
Guariglia, E. (2019). Riemann zeta fractional derivative—functional equation and link with primes. Adv. Difference Equat. 2019, paper no. 261, 15 pp.Google Scholar
Ivanovs, J. (2018). Zooming in on a Lévy process at its supremum. Ann. Appl. Prob. 28, 912–940.CrossRefGoogle Scholar
Jasnovidov, G. and Shemendyuk, A. (2021). Parisian ruin for insurer and reinsurer under quota-share treaty. Preprint. Available at https://arxiv.org/abs/2103.03213.Google Scholar
Ji, L. and Robert, S. (2018). Ruin problem of a two-dimensional fractional Brownian motion risk process. Stoch. Models 34, 73–97.CrossRefGoogle Scholar
Kabluchko, Z. and Wang, Y. (2014). Limiting distribution for the maximal standardized increment of a random walk. Stoch. Process. Appl. 124, 2824–2867.CrossRefGoogle Scholar
Kudryavtsev, L., Kutasov, A., Chehlov, V. and Shabunin, M. (2003). Collection of Problems in Mathematical Analysis, Part 2, Integrals and Series. Phizmatlit, Moscow (in Russian).Google Scholar
Pickands, J., III (1969). Asymptotic properties of the maximum in a stationary Gaussian process. Trans. Amer. Math. Soc. 145, 75–86.Google Scholar
Pickands, J., III (1969). Upcrossing probabilities for stationary Gaussian processes. Trans. Amer. Math. Soc. 145, 51–73.CrossRefGoogle Scholar
Piterbarg, V. I. (1996). Asymptotic Methods in the Theory of Gaussian Processes and Fields. American Mathematical Society, Providence, RI.Google Scholar
Piterbarg, V. I. (2015). Twenty Lectures about Gaussian Processes. Atlantic Financial Press, London, New York.Google Scholar
Wood, D. (1992). The computation of polylogarithms. Tech. Rep. 15-92*, Computing Laboratory, University of Kent.Google Scholar