Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-21T15:22:44.926Z Has data issue: false hasContentIssue false
  • English
  • Français

On wald-type optimal stopping for Brownian motion

Part of: Markov processes Stochastic analysis Stochastic processes

Published online by Cambridge University Press:  14 July 2016

S. E. Graversen  and
G. Peškir
S. E. Graversen*
Affiliation:
University of Aarhus
G. Peškir*
Affiliation:
University of Aarhus
*
∗Postal address: Institute of Mathematics, University of Aarhus, Ny Munkegade, 8000 Aarhus, Denmark.
∗∗Postal address: Institute of Mathematics, University of Aarhus, Ny Munkegade, 8000 Aarhus, Denmark. Also at: Department of Mathematics, University of Zagreb, Bijenička 30, 41000 Zagreb, Croatia.
Get access Rights & Permissions [Opens in a new window]

Abstract

The solution is presented to all optimal stopping problems of the form supτE(G(|Β τ |) – cτ), where 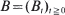is standard Brownian motion and the supremum is taken over all stopping times τ for B with finite expectation, while the map G : ℝ+ → ℝ satisfies 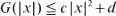for some 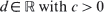being given and fixed. The optimal stopping time is shown to be the hitting time by the reflecting Brownian motion 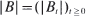of the set of all (approximate) maximum points of the map 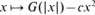. The method of proof relies upon Wald's identity for Brownian motion and simple real analysis arguments. A simple proof of the Dubins–Jacka–Schwarz–Shepp–Shiryaev (square root of two) maximal inequality for randomly stopped Brownian motion is given as an application.

Keywords

BROWNIAN MOTIONOPTIMAL STOPPING TIMEWALD'S IDENTITY FOR BROWNIAN MOTIONBURKHOLDER–GUNDY INEQUALITYDOOB'S OPTIONAL SAMPLING THEOREM

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory 60J65: Brownian motion
Secondary: 60G42: Martingales with discrete parameter 60G44: Martingales with continuous parameter 60H05: Stochastic integrals
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 1 , March 1997 , pp. 66 - 73
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Burkholder, D. L. and Gundy, R. F. (1970) Extrapolation and interpolation of quasi-linear operators on martingales. Acta Math. 124, 249–304.Google Scholar
[2] Dubins, L. E. and Schwarz, G. (1988) A sharp inequality for sub-martingales and stopping times. Astérisque 157-158, 129–145.Google Scholar
[3] Dubins, L. E., Shepp, L. A. and Shiryaev, A. N. (1993) Optimal stopping rules and maximal inequalities for Bessel processes. Theory Prob. Appl. 38, 226–261.Google Scholar
[4] Jacka, S. D. (1991) Optimal stopping and best constants for Doob-like inequalities I: The case p = 1. Ann. Prob. 19, 1798–1821.CrossRefGoogle Scholar
[5] Wald, A. (1945) Sequential tests of statistical hypotheses. Ann. Math. Statist. 16, 117–186.Google Scholar