Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-07-03T23:29:48.843Z Has data issue: false hasContentIssue false
  • English
  • Français

Some asymptotic results for exponential functionals of Brownian motion

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

J.-C. Gruet  and
Z. Shi
J.-C. Gruet*
Affiliation:
Université Paris VI
Z. Shi*
Affiliation:
Université Paris VI
*
∗Postal address: Laboratoire de Probabilités, CNRS URA 224, Université Paris VI, Tour 56, 4 Place Jussieu, 75252 Paris Cedex 05, France and Université de Reims Champagne Ardenne, UFR Sciences, B.P. 1039, 51687 Reims Cedex 2, France.
∗∗Postal address: L.S.T.A.-CNRS URA 1321, Université Paris VI, Tour 45–55, 3e étage, 4 Place Jussieu, 75252 Paris Cedex 05, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

The study of exponential functionals of Brownian motion has recently attracted much attention, partly motivated by several problems in financial mathematics. Let 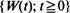be a linear Brownian motion starting from 0. Following Dufresne (1989), (1990), De Schepper and Goovaerts (1992) and De Schepper et al. (1992), we are interested in the process 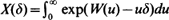(for δ > 0), which stands for the discounted values of a continuous perpetuity payment. We characterize the upper class (in the sense of Paul Lévy) of X, as δ tends to zero, by an integral test. The law of the iterated logarithm is obtained as a straightforward consequence. The process 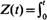exp(W(u))du is studied as well. The class of upper functions of Z is provided. An application to the lim inf behaviour of the winding clock of planar Brownian motion is presented.

Keywords

LAW OF THE ITERATED LOGARITHMLÉVY'S UPPER CLASSEXPONENTIAL FUNCTIONALWINDING CLOCKBROWNIAN MOTION

MSC classification

Primary: 60F15: Strong theorems
Secondary: 60J65: Brownian motion
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 4 , December 1995 , pp. 930 - 940
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertoin, J. and Werner, W. (1994) Asymptotic windings of planar Brownian motion revisited via the Ornstein-Uhlenbeck process. Séminaire de Probabilités XXVIII, ed. Azéma, J., Meyer, P.-A. and Yor, M. pp. 138–152. Lecture Notes in Mathematics 1532, Springer-Verlag, Berlin.Google Scholar
Comtet, A., Desbois, J. and Monthus, C. (1993) Asymptotic laws for the winding angles of planar Brownian motion. J. Statist. Phys. 73, 433–440.CrossRefGoogle Scholar
Csörgö, M. and Rèvèsz, P. (1979) How big are the increments of a Wiener process? Ann. Prob. 7, 731–737.CrossRefGoogle Scholar
De Schepper, A. and Goovaerts, M. (1992) Some further results on annuities certain with random interest. Insurance: Math. Economics 11, 283–290.Google Scholar
De Schepper, A., Goovaerts, M. and Delbaen, F. (1992) The Laplace transform of annuities certain with exponential time distribution. Insurance: Math. Economics 11, 291–294.Google Scholar
Deelstra, G. and Delbaen, F. (1992) Remarks on the methodology introduced by Goovaerts et al. Insurance: Math. Economics 11, 295–299.Google Scholar
Dufresne, D. (1989) Weak convergence of random growth processes with applications to insurance. Insurance: Math. Economics 8, 187–201.Google Scholar
Dufresne, D. (1990) The distribution of a perpetuity, with applications to risk theory and pension funding. Scand. Actuarial J, 39–79.Google Scholar
Geman, H. and Yor, M. (1993) Bessel processes, Asian options and perpetuities. Math. Finance 3, 349–375.Google Scholar
Révész, P. (1990) Random Walk in Random and Non-Random Environments. World Scientific, Singapore.CrossRefGoogle Scholar
Robbins, H. and Siegmund, D. (1972) On the law of the iterated logarithm for maxima and minima. Proc. 6th Berkeley Symp. Math. Statist. Prob. 3, 51–70.Google Scholar
Rogers, L. C. G. and Williams, D. (1987) Diffusions, Markov Processes, and Martingales. Vol II: Itô Calculus. Wiley, Chichester.Google Scholar
Williams, D. (1974) Path decomposition and continuity of local time for one-dimensional diffusions, I. Proc. London Math. Soc. (3) 28, 738–768.Google Scholar
Yor, M. (1992a) Sur certaines fonctionnelles exponentielles du mouvement brownien réel. J. Appl. Prob. 29, 202–208.CrossRefGoogle Scholar
Yor, M. (1992b) Some Aspects of Brownian Motion. Part I: Some Special Functionals. Birkhäuser, Basel.Google Scholar
Yor, M. (1993) From planar Brownian windings to Asian options. Insurance: Math. Economics 13, 23–34.Google Scholar