Hostname: page-component-5c6d5d7d68-xq9c7 Total loading time: 0 Render date: 2024-08-20T12:52:33.730Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic distributions for the Ehrenfest urn and related random walks

Part of: Limit theorems Markov processes Probability theory on algebraic and topological structures Equilibrium statistical mechanics Abstract harmonic analysis

Published online by Cambridge University Press:  14 July 2016

Michael Voit
Michael Voit*
Affiliation:
Universität Tübingen
*
∗Postal address: Mathematisches Institut, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

The distributions of nearest neighbour random walks on hypercubes 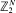in continuous time t 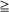0 can be expressed in terms of binomial distributions; their limit behaviour for t, N → ∞ is well-known. We study here these random walks in discrete time and derive explicit bounds for the deviation of their distribution from their counterparts in continuous time with respect to the total variation norm. Our results lead to a recent asymptotic result of Diaconis, Graham and Morrison for the deviation from uniformity for N →∞. Our proofs use Krawtchouk polynomials and a version of the Diaconis–Shahshahani upper bound lemma. We also apply our methods to certain birth-and-death random walks associated with Krawtchouk polynomials.

Keywords

RANDOM WALKS ON HYPERCUBESBIRTH-AND-DEATH RANDOM WALKSKRAWTCHOUKPOLYNOMIALSUNIFORM DISTRIBUTIONTOTAL VARIATION DISTANCEFINITE HYPERGROUPS

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 60F05: Central limit and other weak theorems 60B10: Convergence of probability measures 33C45: Orthogonal polynomials and functions of hypergeometric type (Jacobi, Laguerre, Hermite, Askey scheme, etc.) 82B05: Classical equilibrium statistical mechanics (general) 43A62: Hypergroups
Type
Research Papers
Information
Journal of Applied Probability , Volume 33 , Issue 2 , September 1996 , pp. 340 - 356
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bingham, N. H. (1991) Fluctuation theory for the Ehrenfest urn. Adv. Appl. Prob. 23, 598–611.Google Scholar
[2] Bloom, W. and Heyer, H. (1994) Harmonic Analysis of Probability Measures on Hypergroups. De Gruyter, New York.Google Scholar
[3] Diaconis, P. (1988) Group Representations in Probability and Statistics. Institute of Mathematical Statistics, Hayward, CA.Google Scholar
[4] Diaconis, P., Graham, R. L. and Morrison, J. A. (1990) Asymptotic analysis of a random walk on a hypercube with many dimensions. Rand. Struct. Alg. 1, 51–72.Google Scholar
[5] Diaconis, P. and Hanlon, P. (1992) Eigen analysis for some examples of the Metropolis algorithm. Contemp. Math. 138, 99–117.Google Scholar
[6] Donnelly, P., Lloyd, P. and Sudbury, A. (1994) Approach to stationarity of the Bernoulli-Laplace diffusion model. Adv. Appl. Prob. 26, 715–727.Google Scholar
[7] Dunkl, C. F. and Ramirez, D. E. (1974) Krawtchouk polynomials and the symmetrization of hypergroups. SIAM J. Math. Anal. 5, 351–366.Google Scholar
[8] Feller, W. (1971) An Introduction to Probability Theory and its Applications. Vol. II, 2nd edn. Wiley, New York.Google Scholar
[9] Jewett, R. I. (1975) Spaces with an abstract convolution of measures. Adv. Math. 18, 1–101.Google Scholar
[10] Kac, M. (1947) Random walks and the theory of Brownian motion. Amer. Math. Monthly 54, 369–391.Google Scholar
[11] Karlin, S. and Mcgregor, J. (1965) Ehrenfest urn models. J. Appl. Prob. 2, 352–376.Google Scholar
[12] Krawtchouk, M. (1929) Sur une généralization des polynômes d'Hermite. C.R. Acad. Sci. 189, 620–622.Google Scholar
[13] Letac, G. and Takács, L. (1979) Random walks on the m-dimensional cube. J. Reine Angew. Math. 310, 187–195.Google Scholar
[14] Mathews, P. (1987) Mixing rates for random walks on the cube. SIAM J. Alg. Disc. Math. 8, 746–752.Google Scholar
[15] Mitrinovic, D. S. (1970) Analytic Inequalities. Springer, Berlin.Google Scholar
[16] Ross, K. A. and Xu, D. (1994) Hypergroup deformations and Markov chains. J. Theor. Prob. 7, 813–830.Google Scholar
[17] Szegö, G. (1959) Orthogonal Polynomials. Amer. Math. Soc. Coll. Publ. 23. AMS. Providence, RI.Google Scholar
[18] Voit, M. (1991) Pseudoisotropic random walks on free groups and semigroups. J. Multiv. Anal. 38, 275–293.Google Scholar
[19] Voit, M. (1995) A central limit theorem for isotropic random walks on n-spheres for n ? 8. J. Math. Anal. Appl. 189, 215–224.Google Scholar
[20] Voit, M. (1996) Limit theorems for compact two-point homogeneous spaces of large dimensions. J. Theor. Prob. 9, to appear.Google Scholar