Hostname: page-component-788cddb947-nxk7g Total loading time: 0 Render date: 2024-10-19T21:17:48.590Z Has data issue: false hasContentIssue false
  • English
  • Français

The convergence of a branching Brownian motion used as a model describing the spread of an epidemic

Published online by Cambridge University Press:  14 July 2016

Frank J. S. Wang
Frank J. S. Wang*
Affiliation:
University of Montana
*
∗Postal address: Department of Mathematics, University of Montana, Missoula, Montana 59812, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

A spatial epidemic process where the individuals are located at positions in the Euclidean space R2 is considered. The infective individuals, with an infection period that is exponentially distributed with parameter µ, move in R2 according to a Brownian motion with a diffusion coefficient σ2. The susceptible individuals may also move. But we shall use the approximation that they remain unchanged in numbers and therefore assume that the averaged ‘density' of susceptibles per unit area is the same throughout space and time. The transition probability rate of infection of a susceptible in the infinitesimal element of area dy by an infective in dx is assumed to be a function h(x – y |) of the distance | x – y | between x and y. Then our process can be considered as a two-dimensional birth and death Brownian motion. Let 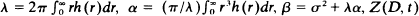be the number of infective individuals in the set D at time t and 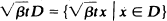. The almost everywhere convergence of the random variables 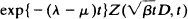to a limit random variable W(D) is established.

Keywords

SPATIAL EPIDEMIC MODELA.E. CONVERGENCEMARTINGALESBROWNIAN MOTIONBRANCHING PROCESS
Type
Research Papers
Information
Journal of Applied Probability , Volume 17 , Issue 2 , June 1980 , pp. 301 - 312
Copyright
Copyright © Applied Probability Trust 1980 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.CrossRefGoogle Scholar
Bailey, N. T. J. (1975) The Mathematical Theory of Infectious Diseases, 2nd edn. Hafner, New York.Google Scholar
Bartlett, M. S. (1960) Stochastic Population Models in Ecology and Epidemiology. Wiley, New York.Google Scholar
Breiman, L. (1968) Probability. Addison-Wesley, Reading, MA.Google Scholar
Harris, T. E. (1963) The Theory of Branching Processes. Springer-Verlag, Berlin.CrossRefGoogle Scholar
Ikeda, N., Nagasawa, M. and Watanabe, S. (1968), (1969) Branching Markov processes I, II, III. J. Math. Kyoto Univ. 8, 233–278, 365–410; 9, 95–160.Google Scholar
Radcliffe, J. (1976) The convergence of a position-dependent branching process used as an approximation to a model describing the spread of an epidemic. J. Appl. Prob. 13, 338–344.CrossRefGoogle Scholar
Srinivasan, S. K. (1969) Stochastic Theory and Cascade Processes. American Elsevier, New York.Google Scholar
Varadham, S. R. S. (1968) Stochastic Processes. Courant Institute of Mathematical Sciences, New York.Google Scholar
Watanabe, S. (1967) Limit theorem for a class of branching processes. In Markov Processes and Potential Theory. (Proc. Symp. Math. Res. Center, Madison, Wisconsin), Wiley, New York, 205–232.Google Scholar