Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-12T19:35:55.246Z Has data issue: false hasContentIssue false
  • English
  • Français

Distribution of the scan statistic for a sequence of bistate trials

Part of: Markov processes Distribution theory - Probability

Published online by Cambridge University Press:  14 July 2016

James C. Fu
James C. Fu*
Affiliation:
University of Manitoba
*
∗ Postal address: Department of Statistics, University of Manitoba, Winnipeg, Manitoba, Canada R3T 2N2. Email address: fu@ccu.umanitoba.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

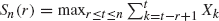Let be the scan statistic of window size r for a sequence of n bistate trials 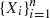. The scan statistic Sn(r) has been successfully used in various fields of applied probability and statistics, and its distribution has been studied extensively in the literature. Currently, all existing formulae for the distribution of Sn(r) are rather complex, and they can only be numerically implemented when 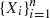is a sequence of Bernoulli trials, the window size r is less than 20 and the length of the sequence n is not too large. Hence, these formulae have been limiting the practical applications of the scan statistic. In this article, we derive a simple and effective formula for the distribution of Sn(r) via the finite Markov chain embedding technique to overcome some of the limitations of the existing complex formulae. This new formula can be applied when 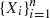is either a sequence of Bernoulli trials or a sequence of Markov dependent bistate trials. Selected numerical examples are given to illustrate our results.

Keywords

Compound patternwaiting time distributionfinite Markov chain embeddingtransition probability matrix

MSC classification

Primary: 60E05: Distributions
Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Papers
Information
Journal of Applied Probability , Volume 38 , Issue 4 , December 2001 , pp. 908 - 916
Copyright
Copyright © by the Applied Probability Trust 2001 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported in part by Grant A-9216 of the Natural Science and Engineering Research Council of Canada.

References

Chao, M. T., and Fu, J. C. (1991). The reliability of a large series system under Markov structure. Adv. Appl. Prob. 23, 894–908.Google Scholar
Chao, M. T., Fu, J. C., and Koutras, M. V. (1995). Survey of reliability studies of consecutive-k-out-of-n:F and related systems. IEEE Trans. Reliab. 44, 120–127.Google Scholar
Chen, J., and Glaz, J. (1997). Approximations and inequalities for the distribution of a scan statistic for 0–1 Bernoulli trials. In Advances in the Theory and Practice of Statistics, eds Johnson, N. L. and Balakrishnan, N., John Wiley, New York, pp. 285–298.Google Scholar
Darling, R. W. R., and Waterman, M. S. (1986). Extreme value distributions for the largest cube in random lattice. SIAM J. Appl. Math. 46, 118–132.Google Scholar
Fu, J. C. (1986). Reliability of consecutive-k-out-of-n:F system with k – 1-step Markov dependence. IEEE Trans. Reliab. 35, 602–606.Google Scholar
Fu, J. C. (1996). Distribution theory of runs and patterns associated with a sequence of multi-state trials. Statist. Sinica 6, 957–974.Google Scholar
Fu, J. C., and Chang, Y. M. (2001). On probability generating functions for waiting time distributions of compound patterns in a sequence of multi-state trials. Tech. Rep., Department of Statistics, University of Manitoba, Canada. To appear in J. Appl. Prob.Google Scholar
Fu, J. C., and Hu, B. (1987). On reliability of large consecutive-k-out-of-n:F system with k – 1-step Markov dependence. IEEE Trans. Reliab. 36, 75–77.Google Scholar
Fu, J. C., and Koutras, M. V. (1994). Distribution theory of runs: a Markov chain approach. J. Amer. Statist. Assoc. 89, 1050–1058.CrossRefGoogle Scholar
Fu, Y. X., and Curnow, R. N. (1990). Locating a changed segment in a sequence of Bernoulli variables. Biometrika 77, 295–304.Google Scholar
Glaz, J. (1989). Approximations and bounds for the distribution of the scan statistic. J. Amer. Statist. Assoc. 84, 560–566.Google Scholar
Glaz, J. (1992). Approximations for tail probabilities and moments of the scan statistic. Comput. Statist. Data Anal. 14, 213–227.Google Scholar
Huntington, R., and Naus, J. (1975). A simple expression for kth nearest neighbor coincidence probabilities. Ann. Prob. 3, 894–896.Google Scholar
Karlin, S., and McGregor, G. (1959). Coincidence probability. Pacific J. Math. 9, 1141–1164.Google Scholar
Koutras, M. V. (1996). On a Markov chain approach for the study of reliability structures. J. Appl. Prob. 33, 357–367.Google Scholar
Koutras, M. V., and Alexandrou, V. A. (1995). Runs, scans, and urn model distributions: a unified Markov chain approach. Ann. Inst. Statist. Math. 47, 743–766.CrossRefGoogle Scholar
Naus, J. I. (1965). The distribution of the size of the maximum cluster of points on a line. J. Amer. Statist. Assoc. 60, 532–538.CrossRefGoogle Scholar
Naus, J. I. (1974). Probabilities for a generalized birthday problem. J. Amer. Statist. Assoc. 69, 810–815.Google Scholar
Naus, J. I. (1982). Approximation for distributions of scan statistics. J. Amer. Statist. Assoc. 77, 177–182.Google Scholar
Saperstein, B. (1972). The generalized birthday problem. J. Amer. Statist. Assoc. 67, 425–428.Google Scholar
Seneta, E. (1981). Nonnegative Matrices and Markov Chains, 2nd edn. Springer, New York.Google Scholar
Sheng, K. N., and Naus, J. I. (1994). Pattern matching between two non-aligned random sequences. Bull. Math. Biol. 56, 1143–1162.Google Scholar